はじめに
本稿は Amazon SageMakerでPythonデータサイエンス入門 の連載記事になります。
その1. Amazon SageMaker の環境構築、事前準備、基礎分析と可視化について
その2. 線形回帰を用いたお弁当の売り上げ予測
その3. 決定木を用いた銀行の顧客ターゲティング ←本稿
以下の Udemy のコースをベースに記事を作成しています。
【ゼロから始めるデータ分析】 ビジネスケースで学ぶPythonデータサイエンス入門
本稿の内容
- 新しいデータの基礎分析
- 決定木を用いた銀行の顧客ターゲティング
- パラメータチューニング
本稿を通して、Python を使用した基本的な決定木分析、パラメータのチューニングについて学べます。
※本稿はその1、その2を読んだことを前提として進めていきます。
新しいデータの基礎分析
まずは、新しく使うデータの基礎分析を行います。
- その1で作成した case2 フォルダーに新しい notebook を作成してください。
モジュールのインポートと設定
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
データの読み込み
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
sample = pd.read_csv("submit_sample.csv",header=None)
testデータの確認
- test の先頭行を確認する。
test.head()
- test の行数と列数を確認する。
train.shape
実行結果
(18083, 17)
- test の欠損地を確認します。
test.isnull().sum()
実行結果
id 0
age 0
job 0
marital 0
education 0
default 0
balance 0
housing 0
loan 0
contact 0
day 0
month 0
duration 0
campaign 0
pdays 0
previous 0
poutcome 0
dtype: int64
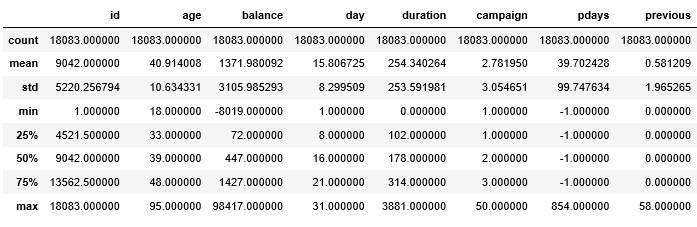
- test 基礎統計量を確認します。
test.describe()
trainデータの確認
- trainの先頭行を確認します。
train.head()
- trainの行数と列数を確認します。
train.shape
実行結果
(27128, 18)
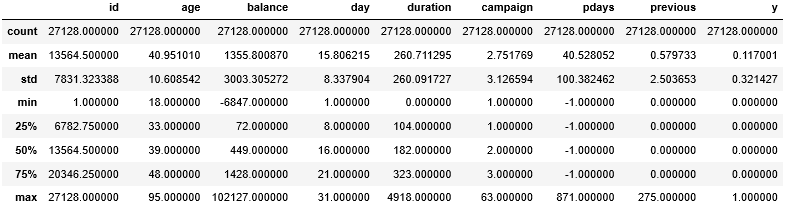
- train の基礎統計量を確認します。
train.describe()
- train の欠損地を確認します。
ここでは各カラムに欠損地がいくつあるか表示して確認します。
train.isnull().sum()
実行結果
id 0
age 0
job 0
marital 0
education 0
default 0
balance 0
housing 0
loan 0
contact 0
day 0
month 0
duration 0
campaign 0
pdays 0
previous 0
poutcome 0
y 0
dtype: int64
- train で y が1の人数を確認します。
train["y"].value_count()
実行結果
0 23954
1 3174
Name: y, dtype: int64
marital と y のクロス集計
- 集計
度数や割合で、集計したデータを要約することです。
数値ではなく、0、1というラベルデータの分布をみるときに便利です。 - クロス集計
集計したデータの設問を掛け合わせて、集計することです。 - クロス集計には pd.crosstab 関数を使います。
- pd.crosstab 関数
()内に( X [" A "], X [" B "])と記述した場合、 A が縦列、 B が横列となります。
オプションで margins=True とすると、総計値のカラムを作成します。
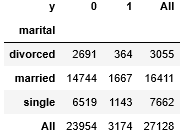
- pd.crosstab 関数
pd.crosstab(train["marital"],train["y"],margins=True)
train の age をビニングする
- ビニング
数値データをグループ1(0より大きい、10以下)、グループ2(10より大きい、20以下)...のように集約することです。 - ビニングにはpd.cut関数を使います。
- pd.cut 関数
()内にビニングしたいデータ、データの区切り方(例えば[0,10,20])の順で書きます。
- pd.cut 関数
- どう区切るか決めるために、age の基本統計量を確認します。
train["age"].describe()
実行結果
count 27128.000000
mean 40.951010
std 10.608542
min 18.000000
25% 33.000000
50% 39.000000
75% 48.000000
max 95.000000
Name: age, dtype: float64
- 結果から0,20,30,40,50,60,100で区切ることにします。
age_bining = pd.cut(train["age"],[0,20,30,40,50,60,100])
- ビニング結果を確認します。
age_bining
実行結果
0 (30, 40]
1 (50, 60]
2 (30, 40]
3 (60, 100]
4 (30, 40]
5 (20, 30]
6 (30, 40]
7 (30, 40]
8 (30, 40]
9 (30, 40]
10 (30, 40]
11 (30, 40]
12 (30, 40]
13 (30, 40]
14 (30, 40]
15 (60, 100]
16 (60, 100]
17 (60, 100]
18 (40, 50]
19 (20, 30]
20 (20, 30]
21 (60, 100]
22 (40, 50]
23 (30, 40]
24 (30, 40]
25 (50, 60]
26 (40, 50]
27 (40, 50]
28 (30, 40]
29 (30, 40]
...
27098 (30, 40]
27099 (20, 30]
27100 (40, 50]
27101 (30, 40]
27102 (30, 40]
27103 (30, 40]
27104 (50, 60]
27105 (40, 50]
27106 (30, 40]
27107 (30, 40]
27108 (30, 40]
27109 (40, 50]
27110 (50, 60]
27111 (40, 50]
27112 (40, 50]
27113 (40, 50]
27114 (40, 50]
27115 (40, 50]
27116 (40, 50]
27117 (20, 30]
27118 (40, 50]
27119 (20, 30]
27120 (60, 100]
27121 (30, 40]
27122 (50, 60]
27123 (40, 50]
27124 (30, 40]
27125 (30, 40]
27126 (30, 40]
27127 (20, 30]
Name: age, Length: 27128, dtype: category
Categories (6, interval[int64]): [(0, 20] < (20, 30] < (30, 40] < (40, 50] < (50, 60] < (60, 100]]
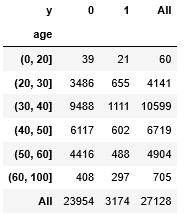
age_bining と y のクロス集計
pd.crosstab(age_bining,train["y"],margins=True)
train の poutcome と y のクロス集計の結果に rate を追加する
- train のデータにある数値データと、質的データがいくつあるか調べます。
train.info()
実行結果
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 27128 entries, 0 to 27127
Data columns (total 18 columns):
id 27128 non-null int64
age 27128 non-null int64
job 27128 non-null object
marital 27128 non-null object
education 27128 non-null object
default 27128 non-null object
balance 27128 non-null int64
housing 27128 non-null object
loan 27128 non-null object
contact 27128 non-null object
day 27128 non-null int64
month 27128 non-null object
duration 27128 non-null int64
campaign 27128 non-null int64
pdays 27128 non-null int64
previous 27128 non-null int64
poutcome 27128 non-null object
y 27128 non-null int64
dtypes: int64(9), object(9)
memory usage: 3.7+ MB
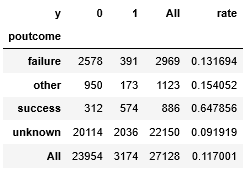
- poutcome と y のクロス集計をします。
pout = pd.crosstab(train["poutcome"],train["y"],margins=True)
- train の poutcome の各値が1となる割合を計算し、 pout に 新たなカラム rate を追加する。
poutcome の各値の合計値から見た1の割合を求めるので、 pout[1] / pout[" All "] で求められる。
pout["rate"] = pout[1]/pout["All"]
pout
train の duration と y のクロス集計の結果に rate を追加する
- train の duration の基礎統計量を確認します。
train["duration"].describe()
実行結果
count 27128.000000
mean 260.711295
std 260.091727
min 0.000000
25% 104.000000
50% 182.000000
75% 323.000000
max 4918.000000
Name: duration, dtype: float64
- duration をビニングします。
区切り方は[-1,100,200,300,400,500,600,700,800,900,1000,5000]とします。
duration_bining = pd.cut(train["duration"],[-1,100,200,300,400,500,600,700,800,900,1000,5000])
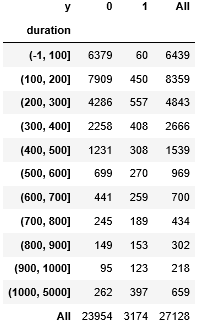
- duration_bining と y でクロス集計をします。
dura = pd.crosstab(duration_bining,train["y"],margins=True)
dura
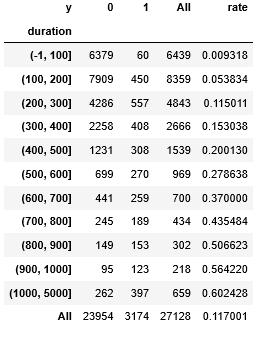
- dura の各値が1となる割合を計算し、 dura に新たなカラム rate を追加します。
dura["rate"] = dura[1]/dura["All"]
dura
決定木を用いた銀行の顧客ターゲティング
銀行の顧客ターゲティングを、機械学習の手法である、決定木を用いて行います。
新しいデータの基礎分析とは別の notebook を使用します。
インポートするモジュールが増えているので、別の notebook を使用することをお勧めします。
機械学習(Machine Learning)とは
データからパータンを学習し、パターンを発見したり、その結果を利用して将来を予測することです。
一般的に予測精度が高く、学習結果が複雑なことが多いです。
また、ハイパーパラメータと呼ばれる変数の調整(パラメータチューニング)が重要になります。
機械学習にはいくつかの種類があります。その中でも有名な2つについて説明します。
-
教師あり学習
入力の正解となるデータがある機械学習。
学習データと結果になるデータをセットで学習する。
例えば、魚の画像を用意して、魚というラベルを付けます。
この画像は魚、という情報を機械に学習させることになります。 -
教師なし学習
入力の正解となるデータがない機械学習。
正解となるラベルがないので、学習データを渡して、データの類似度や規則性に基づいて分類をすることになります。
決定木
質問に対する分岐(基本は2択)を階層的に作っていくことで、判別、回帰を行うモデル。
2択の分岐になるので、人間が理解しやすいです。
しかし、パラメータチューニングを上手にしないと過学習になりやすいです。
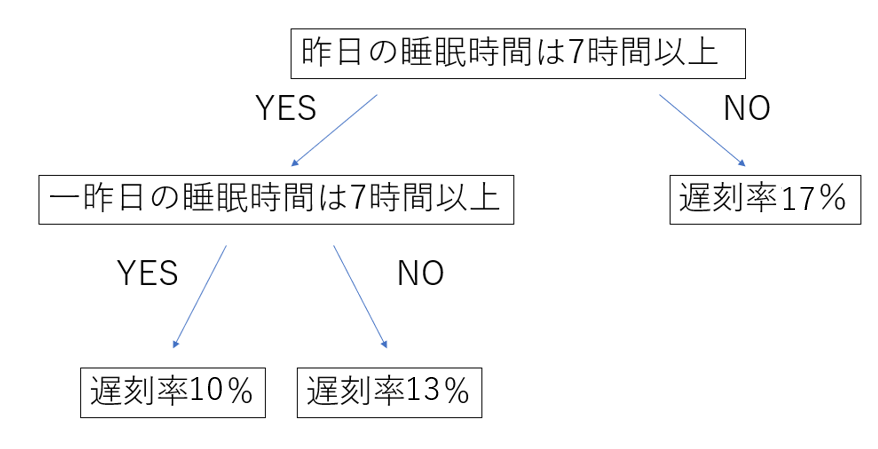
決定木モデルの例を以下に示します。
一番上のノードを根節点、途中のノードを決定節点、これ以上分かれないノードを葉節点といいます。
決定木モデルを作成してみよう
モジュールのインポートと設定
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
from sklearn.tree import DecisionTreeClassifier as DT
from sklearn.tree import export_graphviz
データの読み込み
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
sample = pd.read_csv("submit_sample.csv",header=None)
- trainの先頭行を確認します。
train.head()
train から説明変数の取り出し
- 説明変数は y 以外のすべてのカラムとします。
今までのようにカラムを1つ1つ選択するのは大変なので、ilocを使います。 - iloc
[]内に[開始行:終了行,開始列:終了列]と書くことで、任意の範囲の行、列を指定できます。
開始から終了まですべてを取り出したい場合は、[:]で取り出せます。
trainX = train.iloc[:,0:17]
- trainXを表示してすべての行が代入されているか、確認します。
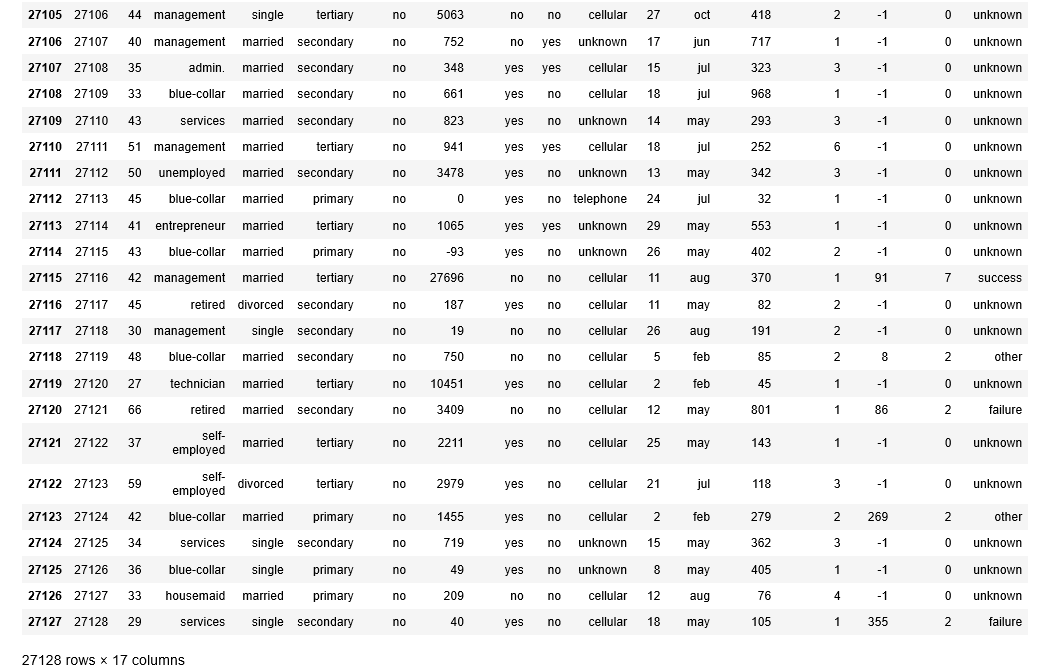
trainX
実行結果
実行結果が多いので、最後の部分のみ載せます。
27128 rows × 17 columns と表示されていることを確認しましょう。
test から説明変数の取り出し
- test の先頭行を確認します。
test.head()
- test には y がないので、すべてのカラムが説明変数となります。
すべてのカラムを代入するためにcopy関数を使用します。
単純にtestX = test としないのはプログラム的な観点のためです。
testX = test.copy()
- testX の中身を確認します。
testX
実行結果
実行結果が多いので、最後の部分のみ載せます。
18083 rows × 17 columns と表示されていることを確認しましょう。
目的変数の取り出し
- y を選択し、変数 y に代入します。
y = train["y"]
- 説明変数のダミー変数化。
trainX = pd.dummies(trainX)
testX = pd.dummies(testX)
- 説明変数がダミー変数化されているか確認します。
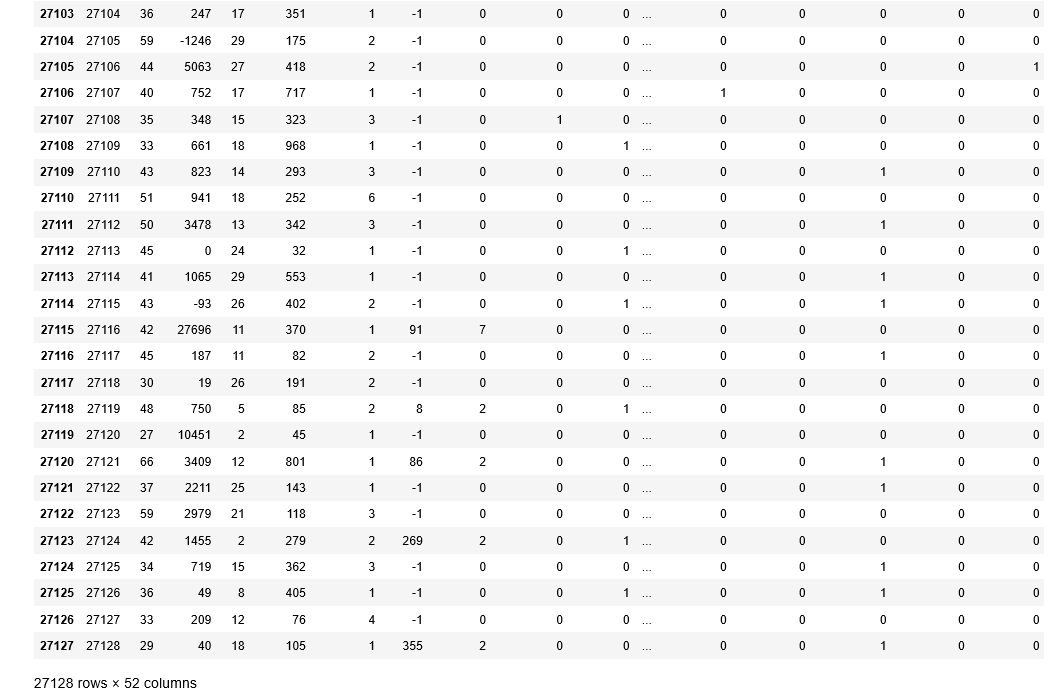
trainX
実行結果
実行結果が多いので、最後の部分のみ載せます。
27128 rows × 52 columns と表示されていることを確認しましょう。
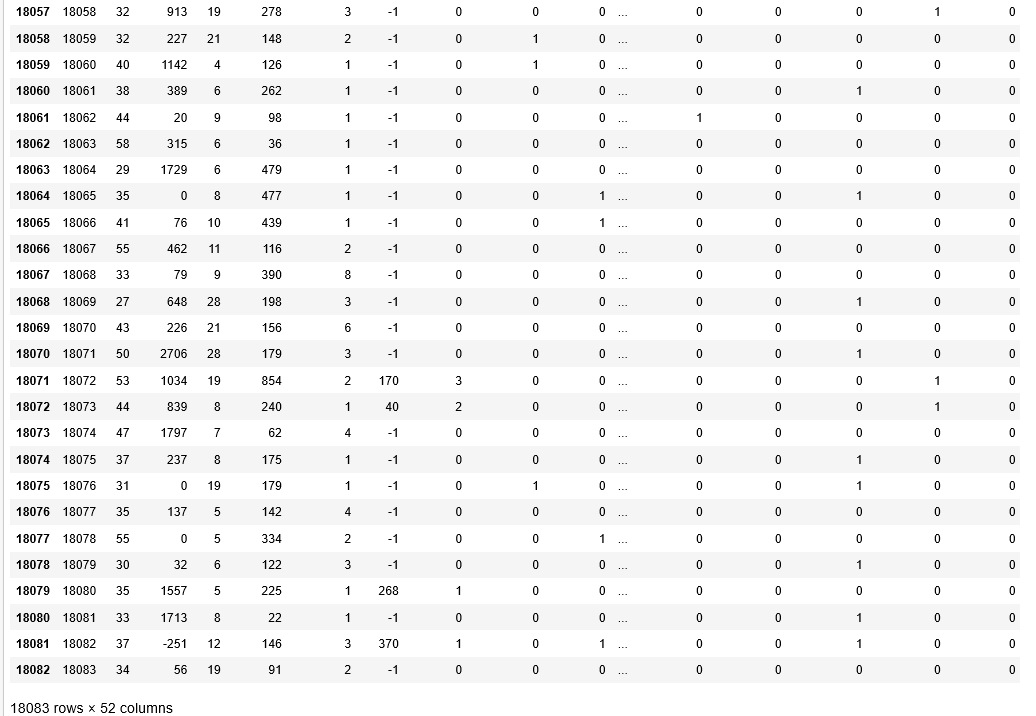
testX
実行結果
実行結果が多いので、最後の部分のみ載せます。
18083 rows × 52 columns と表示されていることを確認しましょう。
決定木モデルの作成
- 決定木モデルの箱を用意します。
変数名はclf1としてDecisionTreeClassifier(決定木分析)を代入します。
オプションとして、機械学習のパラメータを書きます。
今回は max_depth = 2 , min_samples_leaf=500 と書きます。
clf1 = DT(max_depth=2,min_samples_leaf=500)
- 決定木モデルの作成。
fit関数を使用します。
()の中には、説明変数、目的変数の順に書きます。
clf1.fit(trainX,y)
実行結果
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=500, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
作成した木の確認
- 決定木を可視化するために、決定木の図データをdotファイルで書き出します。
その後、dotファイルの中身をコピーしてこちらのサイトに貼り付けて、Generate Graph!を選択してください。 - dotファイルの書き出しにはexport_graphviz関数を使います。
export_graphviz(clf1, out_file="tree.dot", feature_names=trainX.columns, class_names=["0","1"], filled=True, rounded=True)と書きましょう。
export_graphviz(clf1, out_file="tree.dot", feature_names=trainX.columns, class_names=["0","1"], filled=True, rounded=True)
- 可視化した木の確認。
- ノードの見方
1. 分岐の条件
2. ジニ係数(偏り具合を表す)
3. 該当サンプル数
4. 該当サンプルの内訳[0の数、1の数]
5. 条件を満たした場合になんと判断するか(class = 0ということは、口座を開設しないという意味)

予測を行う
- 今回は1である確率を出す必要があるので、predict_proba関数を使います。
- predict_proba関数
各データがそれぞれのクラスに所属する確率を返します。
pred = clf1.predict_proba(testX)
- pred の中身を確認します。
pred
実行結果
array([[0.41565704, 0.58434296],
[0.41565704, 0.58434296],
[0.94135287, 0.05864713],
...,
[0.94135287, 0.05864713],
[0.94135287, 0.05864713],
[0.94135287, 0.05864713]])
左側が0、右側が1の確率です。
testXの1行目の人は、0.41565704の確率で銀行開設しない、逆に言えば0.58434296の確率で銀行を開設する、ということになります。
- 1となる確率を抜き出し、sample[1]に代入して、ファイル出力する。
pred = pred[:.1]
sample[1] = pred
sample.to_csv("submit1_bank.csv",index=None,header=None)
SIGNATEに結果を投稿し、確認
- こちらからSIGNATEのサイトを開いて、Competitionsを選択。

- 練習問題を選択。

- 下にスクロールして、銀行の顧客ターゲティングを選択。

- 投稿を選択。

- ファイルは先ほど作成したsubmit1_bank.csvを選択。
メモにはmax_depth=2、min_samples_leaf=500と書いておきます。

- これで投稿完了です。結果が出るまで2、3分待ちましょう。

- 結果が出ました。
ここでは評価が1に近づくほど精度が良いということになります。
このモデルの精度は0.74ほどなので、まだ精度を上げれます。

決定木のパラメータを変更してみよう
- 新たなモデルの箱を作成。
モデル名はclf2として、パラメータはmax_depth=4, min_samples_leaf=500として、モデルを作成します。
clf2 = DT(max_depth=4,min_samples_leaf=500)
- train と y を使って決定木のモデルを作成します。
clf2.fit(trainX,y)
実行結果
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=4,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=500, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
作成したモデルの可視化
- 先ほどと同様の手順で、モデルを確認します。
export_graphviz(clf2, out_file="tree2.dot", feature_names=trainX.columns, class_names=["0","1"], filled=True, rounded=True)
- dotファイルの中身をコピーしてこちらのサイトに貼り付けて、Generate Graph!を選択してください。

予測を行います
- ここから先の手順は先ほどの手順とほとんど同じなので、コードのみ記述します。
pred2 = clf2.predict_proba(testX) #pred2に代入します
pred2 = pred2[:,1]
sample[1] = pred2
sample.to_csv("submit2_bank.csv",index=None,header=None) #submit2_bank.csvとして出力します
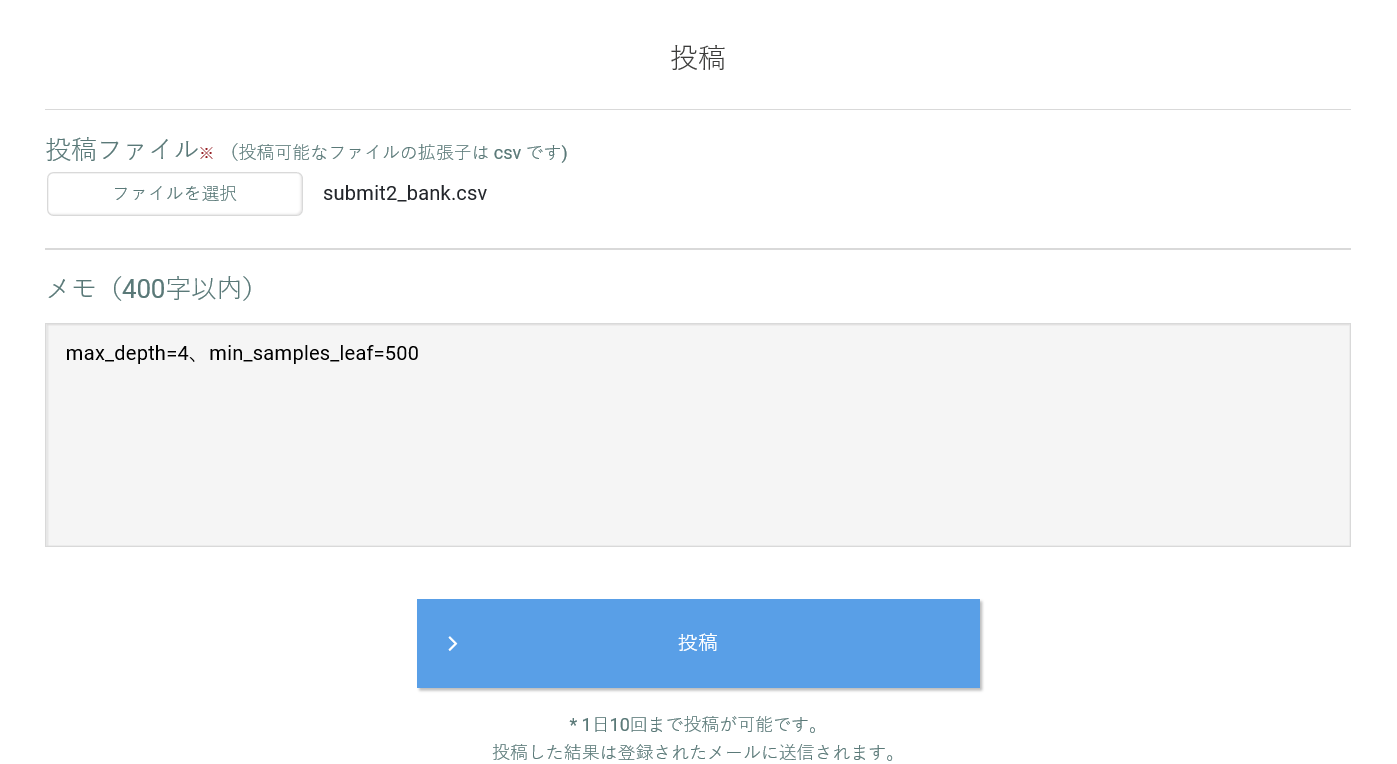
SIGNATEに結果を投稿し、確認
先ほどと同じ手順で SIGNATEにsubmit2_bank.csv を投稿する。
メモにはmax_depth=4、min_samples_leaf=500と書いておきます。
結果が出たら、結果の確認
モデルの精度は84ほどでした。
このようにパラメータを変えるだけで、精度はかなり変わってきます。
パラメータの調整は精度を上げるために、非常に重要ということがわかります。
パラメータのチューニング
先ほど、パラメータの調整が重要ということがわかったので、さらにパラメータの調整を行います。
パラメータとは
-
正確にはハイパーパラメータと呼ばれ、データに合わせて設定しなければならない値。
モデルが複雑になればなるほどパラメータ数は増加する傾向がある。 -
先ほどまで設定していたパラメータは次のような意味を持ちます。

- このパラメータを注意して調整しないと、過学習を起こしてしまう危険がある。
ここでは、過学習しているかしていないかの判別や最適なパラメータのチューニングを行う方法を紹介します。
データは先ほど使ったデータと同じデータを使用します。
データのチューニングは別の notebook で行います。
同じ notebook で作業を行う方は、モジュールのインポートと設定、データの読み込みを飛ばしてください。
モジュールのインポートと設定
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
from sklearn.tree import DecisionTreeClassifier as DT
from sklearn.model_selection import cross_validate
from sklearn.model_selection import GridSearchCV
データの読み込み
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
sample = pd.read_csv("submit_sample.csv",header=None)
説明変数と目的変数の取り出し
- trainX に説明変数として y 以外のカラムを代入します。
testX に testの全てのカラムが説明変数となるので、copy関数を使って取り出します。
y を選択し、変数 y に代入します。
trainX = train.iloc[:,0:17]
testX = test.copy()
y = train["y"]
説明変数をダミー変数化
- trainX と testX をダミー変数化します。
trainX = pd.get_dummies(trainX)
testX = pd.get_dummies(testX)
決定木モデルの箱を作成
- 変数名を clf1 として DT() を代入します。
パラメータは、 max_depth=2 、 min_samples_leaf=500 とします。
clf1 = DT(max_depth=2,min_samples_leaf=500)
クロスバリデーションで clf1 の精度を確認
- クロスバリデーションとは
学習データをk個に分割し、検証をk回繰り返す。
つまり、k個に分割した学習データのうち、k-1個を学習データ(構築データ)としてモデルを作成し、精度を求め、そのモデルを使って、残り1個のデータ(検証データ)でも、精度を求めます。
この手順を他の組み合わせでも行い、k組の平均精度を算出。
この手順で構築データで作成したモデルと、作成したモデルを使った検証データでの精度に差がなければ、妥当性があるということで、過学習していないと推測できます。
クロスバリデーションには、cross_validate関数を使います。 - cross_validate関数
cross_validate(検証したいモデルの変数,説明変数,目的変数,cv=データを何分割するか,scording=評価方法,n_jobs=並列処理をするか(-1でpcの全てのコア数を使ってプログラムを実行する),return_train_score =トレーニングスコアを表示するかどうか)
- オプションにはclf1、 trainX、 y、 cv=5、 scoring="roc_auc" 、 n_jobs=-1 、return_train_score=True と書きます。
cross_validate(clf1,trainX,y,cv=5,scoring="roc_auc",n_jobs=-1,return_train_score=True)
実行結果
train と test に注目すると、どの分割したデータに対してもおおよそ0.75あたりの精度が出ています。
train と test にもあまり差が発生していないので過学習はしていないと推測できます。
{'fit_time': array([0.04482746, 0.05823851, 0.04059458, 0.03797102, 0.03712726]),
'score_time': array([0.00444245, 0.00436449, 0.00284195, 0.00272369, 0.00289845]),
'test_score': array([0.74657601, 0.76182968, 0.73117591, 0.73708019, 0.75909278]),
'train_score': array([0.74534692, 0.74543889, 0.75305367, 0.75162308, 0.74613685])}
異なるパラメータでも精度を確認します。
- パラメータをmax_depth=10, min_samples_leaf=500として、クロスバリデーションをします。
clf2 = DT(max_depth=10,min_samples_leaf=500)
cross_validate(clf2,trainX,y,cv=5,scoring="roc_auc",n_jobs=-1,return_train_score=True)
実行結果
精度はおおむね0.88くらいです。
先ほどと比べ、精度がかなり上がっています。
train と test の差も小さいので過学習をしていないと予測できます。
{'fit_time': array([0.10407352, 0.11838889, 0.09687614, 0.09944749, 0.09311867]),
'score_time': array([0.00457168, 0.00454736, 0.00326657, 0.00388479, 0.00330091]),
'test_score': array([0.88264002, 0.88482571, 0.86778474, 0.89240308, 0.88344359]),
'train_score': array([0.88842017, 0.89038512, 0.89288003, 0.88763037, 0.88561317])}
パラメータのチューニングを楽にしよう
今まで、パラメータをいちいち設定しなおして精度の確認をしてきましたが、それを楽にする方法がグリッドサーチです。
グリッドサーチとは
パラメータの範囲を指定し、その範囲をしらみつぶしに調べることで、最適なパラメータを探索することをグリッドサーチといいます。
- グリッドサーチ+クロスバリデーションの組み合わせは良くパラメータ探索の方法として利用されます。
グリッドサーチ+クロスバリデーションはGridSearchCV関数を使います。
GridSearchCV関数
GridSearchCV(モデルの変数,探索するパラメータの範囲を表す変数,cv=データを何分割するか,scording=評価方法,n_jobs=並列処理をするか(-1でpcの全てのコア数を使ってプログラムを実行する),return_train_score =トレーニングスコアを表示するかどうか)
グリッドサーチに必要な変数の用意
- 決定木モデルの箱を用意します。
特にパラメータの設定はいりません。
clf3 = DT()
- 探索するパラメータの範囲を変数に格納。
max_depth を2から10まで探索します。
parameters = {"max_depth":[2,3,4,5,6,7,8,9,10]}
- range関数を使えば、もう少しスマートに書けます。
どちらを使っても構いませんが、range関数を使うことをお勧めします。
下記のプログラムは上記のプログラムと全くの同義です。
parameters = {"max_depth":list(range(2,11))}
実際にGridSearchCVを使います
- gcv にグリッドサーチの結果を代入し、fit関数を用いて、探索をします。
gcv = GridSearchCV(clf3,parameters,cv=5,scoring="roc_auc",n_jobs=-1,return_train_score=True)
gcv.fit(trainX,y)
実行結果
GridSearchCV(cv=5, error_score='raise',
estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best'),
fit_params=None, iid=True, n_jobs=-1,
param_grid={'max_depth': [2, 3, 4, 5, 6, 7, 8, 9, 10]},
pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
scoring='roc_auc', verbose=0)
グリッドサーチの結果を確認
- cv_results_で結果を確認できます。
gcv.cv_results_
実行結果
{'mean_fit_time': array([0.04312372, 0.05240746, 0.06807289, 0.08054376, 0.09458694,
0.1097723 , 0.12610617, 0.13680182, 0.15077696]),
'std_fit_time': array([0.00567435, 0.00044018, 0.00364806, 0.00082816, 0.00047944,
0.00197029, 0.00278973, 0.00071666, 0.00093721]),
'mean_score_time': array([0.0030582 , 0.00313296, 0.00304751, 0.00304646, 0.00309267,
0.00339885, 0.00326447, 0.00323081, 0.00328884]),
'std_score_time': array([3.23483179e-04, 4.36666309e-04, 5.70462276e-05, 3.06311372e-05,
4.92045581e-05, 4.53471019e-04, 7.05862997e-05, 8.90321504e-05,
1.34748191e-04]),
'param_max_depth': masked_array(data=[2, 3, 4, 5, 6, 7, 8, 9, 10],
mask=[False, False, False, False, False, False, False, False,
False],
fill_value='?',
dtype=object),
'params': [{'max_depth': 2},
{'max_depth': 3},
{'max_depth': 4},
{'max_depth': 5},
{'max_depth': 6},
{'max_depth': 7},
{'max_depth': 8},
{'max_depth': 9},
{'max_depth': 10}],
'split0_test_score': array([0.74657601, 0.82360265, 0.73033016, 0.74058989, 0.74369939,
0.7339222 , 0.72191264, 0.70717536, 0.68883602]),
'split1_test_score': array([0.76182968, 0.82214585, 0.843183 , 0.85330188, 0.85819721,
0.85397308, 0.85806343, 0.8578358 , 0.83931716]),
'split2_test_score': array([0.73117591, 0.8075016 , 0.83351987, 0.84181298, 0.83887095,
0.84215828, 0.83418253, 0.823602 , 0.81577597]),
'split3_test_score': array([0.73708019, 0.75197343, 0.80554008, 0.81561096, 0.82968558,
0.85033815, 0.85055526, 0.84256127, 0.8172142 ]),
'split4_test_score': array([0.75909278, 0.83208758, 0.85796085, 0.86203579, 0.86212914,
0.84641406, 0.83217353, 0.79670877, 0.72302724]),
'mean_test_score': array([0.74715003, 0.80746041, 0.81410356, 0.8226674 , 0.82651383,
0.8253596 , 0.81937653, 0.80557729, 0.77683808]),
'std_test_score': array([0.01195847, 0.02885003, 0.04524916, 0.04391252, 0.04311263,
0.04589021, 0.04970278, 0.05326587, 0.05948148]),
'rank_test_score': array([9, 6, 5, 3, 1, 2, 4, 7, 8], dtype=int32),
'split0_train_score': array([0.74534692, 0.82168836, 0.84726425, 0.85815618, 0.86983919,
0.88435788, 0.9004806 , 0.91375376, 0.92619923]),
'split1_train_score': array([0.74543889, 0.82283293, 0.84962306, 0.86363422, 0.87426809,
0.88432372, 0.89732707, 0.90808259, 0.92257669]),
'split2_train_score': array([0.75305367, 0.82675277, 0.85308818, 0.86695599, 0.87728653,
0.89234865, 0.9037161 , 0.91458628, 0.92669038]),
'split3_train_score': array([0.75162308, 0.77022604, 0.8237681 , 0.83736182, 0.85413452,
0.8843957 , 0.8980002 , 0.90771317, 0.92066021]),
'split4_train_score': array([0.74613685, 0.82072363, 0.84693925, 0.8602002 , 0.87072447,
0.88435383, 0.89524972, 0.90746856, 0.92471486]),
'mean_train_score': array([0.74831988, 0.81244475, 0.84413657, 0.85726168, 0.86925056,
0.88595596, 0.89895474, 0.91032087, 0.92416828]),
'std_train_score': array([0.00332337, 0.02120866, 0.01041868, 0.01039258, 0.00800957,
0.00319643, 0.00290814, 0.00315988, 0.00226381])}
- cv_results_の中で重要な2つを確認します。
重要なのは["mean_train_score"]と["mean_test_score"]です。
それぞれの結果を変数train_score、test_scoreに代入しましょう。
train_score = gcv.cv_results_["mean_train_score"]
test_score = gcv.cv_results_["mean_test_score"]
train_score と test_score の可視化
- x軸をmax_depth、y軸をauc(精度)としてグラフを描きます。
何も設定しないとx軸は0からスタートとなり、実際の値とずれてしまうので、調整が必要です。
調整をする為には、plt.xticks([0,1],[2,3])のように書きます。
上記のオプションの意味は何もしない時に0のものを2とし、1のものを3とする、という意味になります。
今回はmax_depthを2~10まで調べたので9点あります。
plt.plot(train_score)
plt.plot(test_score)
plt.xticks(list(range(0,10)),list(range(2,11)))
実行結果
青色が構築データで作成したモデルの精度を表しています。
オレンジ色が作成したモデルを使った、検証データでの精度を表しています。
- 構築データで作成するモデルは学習すればするほど、構築データに合うモデルになるので、深さが大きくなるほど精度は上がっています。
しかし、構築データに合うモデルが未知の検証データに合うわけではありません。
図からもわかるように深さ6までは精度が上がっていましたが、それ以降は精度が下がっています。
つまり、作成したモデルは深さ7以降で、過学習を起こしている傾向にあり、深さ6のモデルが一番精度の良いモデルといえます。

グリッドサーチで選ばれたパラメータの確認
先ほどは目視で、深さ6が良いモデルだと決定しましたが、best_parames_で最適な結果を確認できます。
gcv.best_params_
実行結果
{'max_depth': 6}
test の予測
- gcv も predict_proba 関数を持っており、自動的に最適なパラメータを使ったモデルで予測がされます。
pred = gcv.predict_proba(testX)
sample に結果を代入してファイル出力
ここから先の手順は先ほどとほとんど同じなので、コードのみ記述します。
pred = pred[:,1]
sample[1] = pred
sample.to_csv("submit3_bank.csv",index=None,header=None)
SIGNATE に結果を投稿し、確認
先ほどと同じ手順で SIGNATEに submit3_bank.csv を投稿する。
メモには max_depth=6 と書いておきます。
結果が出たら、結果を確認
精度は0.86ほどです。
前回と比べても精度が上がっています。
さらに精度を上げるために、次はパラメータを増やして、グリッドサーチをしてみましょう

パラメータを追加して、グリッドサーチをしよう
グリッドサーチで最適なパラメータを max_depth (深さ) だけに焦点を置いて算出しました。
次は min_samples_leaf (葉に属する最小サンプル数) も同時に最適なパラメータを探しましょう。
グリッドサーチに必要な変数の用意
- 決定木モデルの箱を用意。
clf4 = DT()
- 探索するパラメータの範囲を変数に格納。
max_depthは2~10まで、min_samples_leafは[5,10,20,50,100,500]にします。
parameters2 = {"max_depth":list(range(2,11)),"min_samples_leaf":[5,10,20,50,100,500]}
グリッドサーチ+クロスバリデーションで最適なパラメータを探索
gcv2 = GridSearchCV(clf4,parameters2,cv=5,scoring="roc_auc",n_jobs=-1)
gcv2.fit(trainX,y)
実行結果
GridSearchCV(cv=5, error_score='raise',
estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best'),
fit_params=None, iid=True, n_jobs=-1,
param_grid={'max_depth': [2, 3, 4, 5, 6, 7, 8, 9, 10], 'min_samples_leaf': [5, 10, 20, 50, 100, 500]},
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring='roc_auc', verbose=0)
- 最適なパラメータの確認をします。
gcv2.best_params_
実行結果
{'max_depth': 10, 'min_samples_leaf': 50}
予測を行います
pred2 = gcv2.predict_proba(testX) #pred2に代入
pred2 = pred2[:,1]
sample[1] = pred2
sample.to_csv("submit4_bank.csv",index=None,header=None) #submit4_bank.csvとして出力
SIGNATE に結果を投稿し、確認
先ほどと同じ手順で SIGNATEに submit4_bank.csv を投稿する。
メモには max_depth=10 、 min_samples_leaf=50 と書いておきます。
結果が出たら、結果を確認
精度は0.89ほどです。
先ほどと比べても精度の良いモデルが作れたことがわかります。
おわりに
今回はpythonでプログラミングをしながら、銀行の顧客ターゲティングを決定木で行いました。
udemy の内容はここまでとなっております。
今後も、学習ログを投稿していきますので、よろしくお願いいたします。