はじめに
前回の続きで,公式チュートリアルに沿ってPythonライブラリStimを使ってみる.
今回は表面符合の視覚化や閾値の推定を行う.
前回の記事
公式チュートリアル(英語)
前回の振り返りとタスク管理モジュール
前回は,.Circuit.generatedで回路を作り,.compile_detector_sampleでディテクタのサンプラーを定義し,pymatchingからデコーダを呼び出した.また,それらを使って何回かshotを打ち,論理エラー率を求めた.
これらのタスクをまとめてやってくれるのがsinterというモジュールで,最初にこれを使って前回の最後にやったことを実行する.
まずはインポートから.
%pip install sinter
import sinter
from typing import List
それではタスクを記述していく.
tasks = [
sinter.Task(
circuit=stim.Circuit.generated(
"repetition_code:memory",
rounds=d * 3,
distance=d,
before_round_data_depolarization=noise,
), json_metadata={'d': d, 'p': noise},
)
for d in [3, 5, 7, 9]
for noise in [0.05, 0.08, 0.1, 0.2, 0.3, 0.4, 0.5]
]
collected_stats: List[sinter.TaskStats] = sinter.collect(
num_workers=4,
tasks=tasks,
decoders=['pymatching'],
max_shots=100_000,
max_errors=500,
)
符合距離が3, 5, 7, 9の4種,ランダムパウリエラー率が0.05, 0.08, 0.1, 0.2, 0.3, 0.4, 0.5の7種で,反復符号を作り,100000 shot打つというタスクを記述した.やっていること自体は前回の最後の方にやったこととほとんど同じである.
では,前回と同じくエラー率と論理エラー率をグラフにプロットしてみよう.
sinter.plot_error_rateは,グラフ上にエラー率のプロットをしてくれるメソッドで,不確かさの推定も自動的にやってくれる.
fig, ax = plt.subplots(1, 1)
sinter.plot_error_rate(
ax=ax,
stats=collected_stats,
x_func=lambda stats: stats.json_metadata['p'],
group_func=lambda stats: stats.json_metadata['d'],
)
ax.set_ylim(1e-4, 1e-0)
ax.set_xlim(5e-2, 5e-1)
ax.loglog()
ax.set_title("Repetition Code Error Rates (Phenomenological Noise)")
ax.set_xlabel("Phyical Error Rate")
ax.set_ylabel("Logical Error Rate per Shot")
ax.grid(which='major')
ax.grid(which='minor')
ax.legend()
fig.set_dpi(120)
実行結果

前回と同じようなグラフが得られたが,sinterモジュールを使うことで前回よりも簡易に記述することができた.
表面符号の視覚化
今までは簡単のために古典誤り訂正で用いられる反復符号を使ったが,いよいよ表面符号の本格的な使い方を見ていく.
まずは回路を記述する.
surface_code_circuit = stim.Circuit.generated(
"surface_code:rotated_memory_z",
rounds=9,
distance=3,
after_clifford_depolarization=0.001,
after_reset_flip_probability=0.001,
before_measure_flip_probability=0.001,
before_round_data_depolarization=0.001)
繰り返し数9,符合距離3の表面符号を記述した.1回目の記事では,符合距離9で作ってみたら規模が大きくなりすぎたので小さめの設定になっている.また,エラーの種類も増やしてみる.
after_clifford_depolarizationは,クリフォードゲートを通したあとに一定の確率でランダムパウリエラーを発生させるというもの.after_reset_flip_probabilityは,量子ビットを初期化した際に一定の確率でビット反転エラーが起きるというもの.その他のエラーは以前使ったエラーと同じだ.
では,回路を視覚化してみよう.上から順に,時刻ごとにスライスしたもの,3Dにしたものである.
surface_code_circuit.without_noise().diagram("timeslice-svg")
surface_code_circuit.without_noise().diagram("timeline-3d")
実行結果


実行結果は一部を抜粋した.
次にdetector slice diagramというものを書いてみる.これは,スタビライザの検査がどのようにされているのかを表示するものである.
surface_code_circuit.diagram("detslice-svg")
surface_code_circuit.without_noise().diagram(
"detslice-with-ops-svg",
tick=range(0, 9),)
surface_code_circuit.diagram("matchgraph-3d")
実行結果



回路の中でどのようにスタビライザチェックがされているのかがなんとなくわかると思う.
表面符号による誤り訂正と閾値推定
最後にこの表面符号を使って誤りを訂正してみよう.まずは,タスクを書き直す.
surface_code_tasks = [
sinter.Task(
circuit = stim.Circuit.generated(
"surface_code:rotated_memory_z",
rounds=d * 3,
distance=d,
after_clifford_depolarization=noise,
after_reset_flip_probability=noise,
before_measure_flip_probability=noise,
before_round_data_depolarization=noise,
),
json_metadata={'d': d, 'r': d * 3, 'p': noise},
)
for d in [3, 5, 7]
for noise in [0.008, 0.009, 0.01, 0.011, 0.012]
]
collected_surface_code_stats: List[sinter.TaskStats] = sinter.collect(
num_workers=4,
tasks=surface_code_tasks,
decoders=['pymatching'],
max_shots=1_000_000,
max_errors=5_000,
print_progress=True,
)
これを実行すると,回路の定義からエラー訂正付きのサンプリングまで一気にできる.あとはこれをグラフにかく.
fig, ax = plt.subplots(1, 1)
sinter.plot_error_rate(
ax=ax,
stats=collected_surface_code_stats,
x_func=lambda stat: stat.json_metadata['p'],
group_func=lambda stat: stat.json_metadata['d'],
failure_units_per_shot_func=lambda stat: stat.json_metadata['r'],
)
ax.set_ylim(5e-3, 5e-2)
ax.set_xlim(0.008, 0.012)
ax.loglog()
ax.set_title("Surface Code Error Rates per Round under Circuit Noise")
ax.set_xlabel("Phisical Error Rate")
ax.set_ylabel("Logical Error Rate per Round")
ax.grid(which='major')
ax.grid(which='minor')
ax.legend()
fig.set_dpi(120)
実行結果
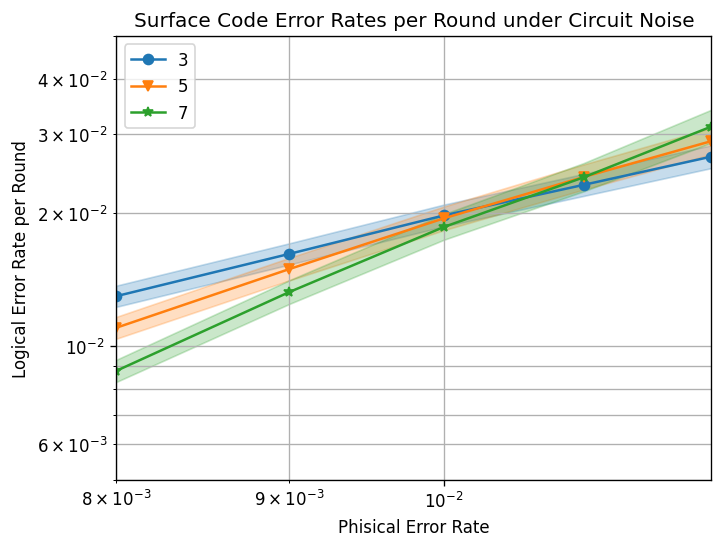
閾値が大体1%ぐらいで,閾値よりもエラー率が小さいと,符合距離やエラー率により論理エラー率が指数で下がることがわかる.
今,エラー率と符合距離を決めた時に論理エラー率がどうなるかを求めたが,実用的な問題としてエラー率と達成したい論理エラー率を決めた時にどのぐらいの符合距離に設定すれば達成できるかという問題を考える.
先ほどと同様にタスクを定義して実行する.
noise = 1e-3
surface_code_tasks = [
sinter.Task(
circuit = stim.Circuit.generated(
"surface_code:rotated_memory_z",
rounds=d * 3,
distance=d,
after_clifford_depolarization=noise,
after_reset_flip_probability=noise,
before_measure_flip_probability=noise,
before_round_data_depolarization=noise,
),
json_metadata={'d': d, 'r': d * 3, 'p': noise},
)
for d in [3, 5, 7]
]
collected_surface_code_stats: List[sinter.TaskStats] = sinter.collect(
num_workers=4,
tasks=surface_code_tasks,
decoders=['pymatching'],
max_shots=5_000_000,
max_errors=100,
print_progress=True,
)
これで,エラー率を0.1%に固定した時それぞれの符合距離で論理エラー率がどうなるかのサンプリングができた.あとは傾きを求めてグラフにする.
import scipy.stats
xs = []
ys = []
log_ys = []
for stats in collected_surface_code_stats:
d = stats.json_metadata['d']
if not stats.errors:
print(f"Didn't see any errors for d={d}")
continue
per_shot = stats.errors / stats.shots
per_round = sinter.shot_error_rate_to_piece_error_rate(per_shot, pieces=stats.json_metadata['r'])
xs.append(d)
ys.append(per_round)
log_ys.append(np.log(per_round))
fit = scipy.stats.linregress(xs, log_ys)
print(fit)
fig, ax = plt.subplots(1, 1)
ax.scatter(xs, ys, label=f"sampled logical error rate at p={noise}")
ax.plot([0, 25],
[np.exp(fit.intercept), np.exp(fit.intercept + fit.slope * 25)],
linestyle='--',
label='least squares line fit')
ax.set_ylim(1e-12, 1e-0)
ax.set_xlim(0, 25)
ax.semilogy()
ax.set_title("Projecting distance needed to survive a trillion rounds")
ax.set_xlabel("Code Distance")
ax.set_ylabel("Logical Error Rate per Round")
ax.grid(which='major')
ax.grid(which='minor')
ax.legend()
fig.set_dpi(120)
実行結果

これで,エラー率が0.1%のときの符号距離と論理エラー率の関係をグラフで表すことができた.
おわりに
もとにしたチュートリアルが割と前提知識多めだったので最後の方はわりと何やってるか曖昧になってしまった部分はあったが,定性的には十分理解できたように思う.
何か間違いがあれば指摘していただけるとありがたいです.
以上.