まえがき
以前単振り子の数値的エネルギー保存性について考察しましたが、その延長として多重振り子を考えてみました。
同様に丸め誤差の範囲でエネルギーを保存するスキームを導出し、計算結果(保存性と精度)を示します。
実装はこちらです。
TL;DR
単振り子の場合と同様にエネルギー保存式を起点として離散化することで、数値的にエネルギーを保存するスキームを構築できます。
ただし$\mathcal{O} \left( N^3 \right)$が収束計算の中に入り込み、計算が重たいです。
上のページのようにリアルタイムで可視化することを考えると、$N$が大きい場合(例えば$N > 16$)は非現実的だと思います。
支配方程式(連続)
まずは連続空間での支配方程式を示しますが、煩雑なためかなり省略しています。
詳細の必要があればドキュメントをご覧ください。
鉛直方向に加速度$g$が加えられている二次元空間の原点を中心とし、$N$個の質点が連なった多重振り子を考えます。
簡単のため原点と質点、および隣り合う質点同士は長さが$l$で質量の無い剛体棒で繋がっているとし、全ての質点の質量は等しく$m$とします。
角度$\theta_i$を変数とする$N$自由度の系に対するLagrangeの式
\frac{d}{dt} \frac{\partial L}{\partial \omega_i}
-
\frac{\partial L}{\partial \theta_i}
=
0
は、運動エネルギー
T
=
\frac{1}{2} m l^2
\sum_{j = 0}^{N - 1}
\sum_{k = 0}^{N - 1}
\left\{ N - \max \left( j, k \right) \right\}
\omega_{j}
\omega_{k}
\cos \left( \theta_{j} - \theta_{k} \right),
位置エネルギー
U
=
-
m g l
\sum_{j = 0}^{N-1}
\left( N - j \right)
\sin{\theta_{j}}
を用いて
m l^2
\sum_{j = 0}^{N - 1}
\left\{ N - \max \left( i, j \right) \right\}
\frac{d \omega_{j}}{d t}
\cos \left( \theta_{i} - \theta_{j} \right)
+
m l^2
\sum_{j = 0}^{N - 1}
\left\{ N - \max \left( i, j \right) \right\}
\omega_{j}
\omega_{j}
\sin \left( \theta_{i} - \theta_{j} \right)
-
m g l
\left( N - i \right)
\cos \theta_{i}
=
0_{i}
と求まります。ここで$\omega_i$は角速度
\frac{d\theta_i}{dt}
です。
一方で全エネルギーの保存は
\frac{dE}{dt}
=
\sum_{{i} = 0}^{N - 1}
\omega_{i}
\left(
\frac{d}{dt} \frac{\partial L}{\partial \omega_i}
-
\frac{\partial L}{\partial \theta_i}
\right)
=
0
で、括弧の中がLagrangeの式から0となり、確かに系の全エネルギーが保存されることがわかります。
以下の離散化においては、このエネルギー保存式とLagrangeの式の関係を重視します。
無次元化
ここまでの式は次元的な正しさのために$g,l,m$のパラメータを含んで議論しましたが、長さスケール$l$と時間スケール$\sqrt{l / g}$を用いて無次元化することで系は一意に決まります。
要するに全て$1$とおいても一般性を失わないので、以下ではそのように扱います。
支配方程式(離散)
次に上の議論の離散化を考えます。
簡単のため離散時間$n$ステップと$n+1$ステップでの差分と補間をそれぞれ
\delta q
\equiv
q^{n+1}
-
q^{n },
\overline{q}
\equiv
\frac{1}{2}
q^{n+1}
+
\frac{1}{2}
q^{n }
と定義しておきます。
通常はLagrangeの式を直接離散化しますが、今回はエネルギー保存式
E
=
T + U
=
const.
を離散化の出発点とします。
「離散的にエネルギーが保存される」というのは、これが$n$ステップから$n+1$ステップに更新された際に変化しないこと、つまり
\frac{\delta E}{\delta t}
\equiv
\frac{
E^{n+1}
-
E^{n }
}{
t^{n+1}
-
t^{n }
}
=
0
となります。
単振り子の場合に示したように、三角関数の微分関係
\frac{d}{dt} \cos \theta
=
-
\omega
\sin \theta,
\frac{d}{dt} \sin \theta
=
\omega
\cos \theta,
は離散化した場合成立せず、
\frac{\delta}{\delta t} \cos \theta
=
-
\overline{\omega}
\text{sinc} \frac{\delta \theta}{2}
\sin \overline{\theta},
\frac{\delta}{\delta t} \sin \theta
=
\overline{\omega}
\text{sinc} \frac{\delta \theta}{2}
\cos \overline{\theta},
となります。
また積の微分公式
d \left( f \cdot g \right)
=
df \cdot g
+
f \cdot dg
は差分では
\delta \left( f \cdot g \right)
=
\delta f \cdot \overline{g}
+
\overline{f} \cdot \delta g
とする必要があります。
こういった離散化誤差に注意しつつ頑張って計算しますと、離散化されたエネルギーの式として以下が得られます。
\frac{\delta E}{\delta t}
=
\sum_{i = 0}^{N - 1}
\overline{\omega_i}
Q_i
=
0,
ここで
Q_i
\equiv
\sum_{j = 0}^{N - 1}
\left\{
N
-
\max \left( i, j \right)
\right\}
\frac{\delta \omega_{j}}{\delta t}
\overline{\cos \left( \theta_i - \theta_j \right)}
\left(
\frac{1}{2}
+
\frac{1}{2}
\frac{
\overline{
\omega_{i}
\cos \left( \theta_i - \theta_j \right)
}
}{
\overline{\omega_{i}}
\,
\overline{\cos \left( \theta_i - \theta_j \right)}
}
\right)
+
\sum_{j = 0}^{N - 1}
\left\{
N
-
\max \left( i, j \right)
\right\}
\overline{\omega_{j}}
\,
\overline{\omega_{j}}
\text{sinc} \left(
\frac{
\delta{\theta_{i}}
}{2}
-
\frac{
\delta{\theta_{j}}
}{2}
\right)
\sin \left( \overline{\theta_{i}} - \overline{\theta_{j}} \right)
-
\left( N - i \right)
\text{sinc} \frac{\delta{\theta_{i}}}{2}
\cos \overline{\theta_{i}}
と置きました。
連続空間での議論から、この$Q_i$はLagrangeの式の左辺であるべきです。
よってエネルギー保存性を内包した離散化Lagrangeの式
Q_i = 0_i
が得られます。
それぞれの項に着目すると、連続空間と離散空間では以下のような対応があることが見て取れます。
- Mass matrixに由来する項
\begin{aligned}
&
\sum_{j = 0}^{N - 1}
\left\{ N - \max \left( i, j \right) \right\}
\frac{d \omega_{j}}{d t}
\cos \left( \theta_{i} - \theta_{j} \right) \\
&
\approx \\
&
\sum_{j = 0}^{N - 1}
\left\{
N
-
\max \left( i, j \right)
\right\}
\frac{\delta \omega_{j}}{\delta t}
\overline{\cos \left( \theta_i - \theta_j \right)}
\left(
\frac{1}{2}
+
\frac{1}{2}
\frac{
\overline{
\omega_{i}
\cos \left( \theta_i - \theta_j \right)
}
}{
\overline{\omega_{i}}
\,
\overline{\cos \left( \theta_i - \theta_j \right)}
}
\right)
\end{aligned}
各変数を近似した上で最後に修正項が加わっています。
一般に積の平均(分子)と平均の積(分母)は異なりますが、$\Delta t \rightarrow 0$の極限で両者は一致するため、確かに連続空間での式の離散化となっていることがわかります。
- 非線形項
\begin{aligned}
&
\sum_{j = 0}^{N - 1}
\left\{ N - \max \left( i, j \right) \right\}
\omega_{j}
\omega_{j}
\sin \left( \theta_{i} - \theta_{j} \right) \\
&
\approx \\
&
\sum_{j = 0}^{N - 1}
\left\{
N
-
\max \left( i, j \right)
\right\}
\overline{\omega_{j}}
\,
\overline{\omega_{j}}
\text{sinc} \left(
\frac{
\delta{\theta_{i}}
}{2}
-
\frac{
\delta{\theta_{j}}
}{2}
\right)
\sin \left( \overline{\theta_{i}} - \overline{\theta_{j}} \right)
\end{aligned}
三角関数の差分にともなう修正が$\text{sinc}$関数として現れています。
$\delta \theta$は$\Delta t \rightarrow 0$で$0$より、これも極限で元の式に帰着します。
- 位置エネルギー項
\begin{aligned}
&
\left( N - i \right)
\cos \theta_{i} \\
&
\approx \\
&
\left( N - i \right)
\text{sinc} \frac{\delta{\theta_{i}}}{2}
\cos \overline{\theta_{i}}
\end{aligned}
単振り子で議論した点と同じです。
これも極限で元の式に帰着します。
またこの式を導出する中で
\frac{\delta \theta_i}{\delta t}
=
\overline{\omega_i}
(Crank-Nicolson法)が必要であることが自然と導かれます。
精度については次の章で議論します。
結果
前の章で導出した式の保存性と精度について実際の計算結果を示します。
コストと複雑度のバランスから$N = 8$を考えます。
初期条件として質点が全て水平一列に並んだ状態($\theta_i = 0$)を考え、(無次元)速度に$\omega_i = \sqrt{6 / \left( 2N+1 \right)}$を与えます。
これは運動エネルギーが全て位置エネルギーに変換されたと仮定した場合に、質点が鉛直方向に一列に静止して並ぶ条件です。
もちろんこの状態は不安定なので、初期条件として与える場合や$N = 1$(単振り子)の場合を除いて生じませんが、鉛直上向きと下向きで静止した状態がそれぞれ$E=1$と$E=0$となり、正規化に都合がいいのでこのように設定しました。
エネルギー保存性
固有振動の時間と比べて十分長く$t = 10^3$まで積分することとします。
単純なスキーム
比較のため、単純な離散化として
\sum_{j = 0}^{N - 1}
\left\{ N - \max \left( i, j \right) \right\}
\frac{\delta \omega_{j}}{\delta t}
\cos \left( \theta_{i}^n - \theta_{j}^n \right)
=
\left( N - i \right)
\cos \theta_{i}^n
-
\sum_{j = 0}^{N - 1}
\left\{ N - \max \left( i, j \right) \right\}
\omega_{j}^n
\omega_{j}^n
\sin \left( \theta_{i}^n - \theta_{j}^n \right),
\frac{\delta \theta_{i}}{\delta t}
=
\omega_{i}^{n+1}
を考えます。
はじめの式で$\omega_i$を更新するのに使用される情報が全て既知のため、一度線形方程式を解くことで時間積分が完了する非常に効率のよい(とはいえ$\mathcal{O} \left( N^3 \right)$)スキームです。
ふたつめの式での角度の更新は、単振り子で正準変換である場合を参考に、オイラー陰解法を用いています(すでに$\omega_i^{n+1}$が求まっているのでゼロコストです)。
エネルギーを描画すると以下のグラフが得られます。
| 運動、位置、全エネルギー | 全エネルギーのみ、最後まで |
|---|---|
 |
 |
$t = 10^2$までを示した左の図は悪くないように見えますが、横一直線であるべき全エネルギー(黒線)はわずかながら振動していて保存していないことがわかります。
特に$t = 10^3$まで積分する(右の図)と、おおよそ単調減少の傾向が見られ、最終的には(散逸系でないにも関わらず)エネルギーを25%程失うことがわかります。
時間刻みを小さくとったり、高次のスキーム(例えばRunge-Kutta法)を用いることで誤差は低減できますが、丸め誤差レベルまで減らすのは難しいでしょう。
エネルギー保存スキーム
上で導出した離散化の下、同様にエネルギーをプロットすると以下のようになります。
| 運動、位置、全エネルギー | 全エネルギー、最後まで |
|---|---|
 |
 |
エネルギーがおおよそ丸め誤差($10^{-12}$程度)で保存していることが確認できます。
精度
エネルギー保存スキームの時間精度を確認するため、$\delta t$の大きさを変化させ、最後の質点の角度の収束を見ることとします。
$t = 10^3$まで積分して最終位置を比較するのが筋ですが、カオス系ゆえにあらゆる擾乱が増幅されてしまい、(統計的には同様ですが)各々の軌跡などは全く違った結果になってしまいます。
したがってカオス現象が発現する前の$t = 4$まで積分し、最終位置を比較することとします。
時間刻み$\delta t$として$128, 256, 512, 1024, 2048, 4096$の逆数を考え、Richardson extrapolationによって得られた$\delta t \rightarrow 0$の擬似的な理論解との誤差を以下に示します。
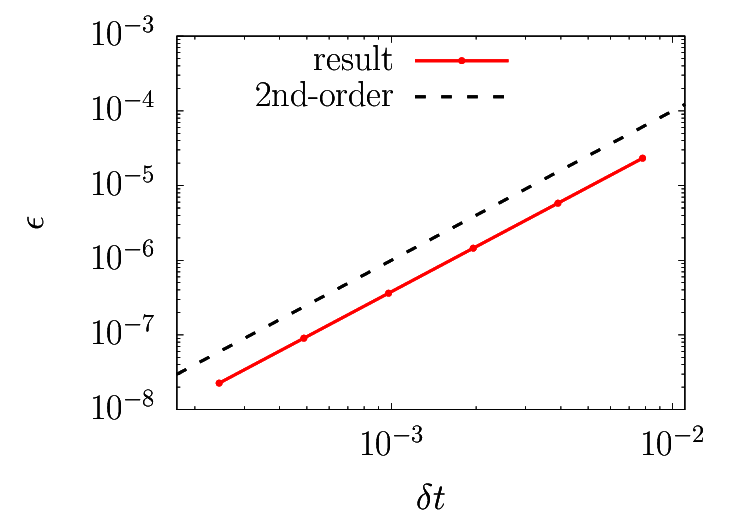
二次精度の差分や補間をベースにしていることから推察できるように、時間二次精度であることが確認できます。
実装
WebAssemblyとの相性の良さからRustで実装しています。
アルゴリズムはそれほど複雑ではないですが、以下にいくつかポイントを挙げます。
線形方程式
どちらのスキームにも線形方程式
\sum_{j = 0}^{N - 1} A_{ij} x_j = b_i
が含まれ、できれば反復解法(例えばconjugate-gradient法)で計算量を減らしたいところです。
ただ質点同士を剛体棒で接続していることから、一点の変化は他の全ての点の運動に影響を及ぼす(すなわちmass matrixは密行列)こととなり、結果反復したところで直接解くのと大差ない硬い方程式になっています。
いずれにせよエネルギー保存性を担保するためには正確に解くことが求められ、直接解法(Gauss elimination)で愚直に解いています。
なお単純なスキームの場合は(おそらく)正定値対称行列なので、微差ですがCholesky分解を用いて計算量を半分にできます。
収束計算
単純なスキームでは$A_{ij}$も$b_i$も既知なので線形方程式を解いて終わりですが、エネルギー保存スキームでは共に未知量を含むため、収束するまでの反復が必須です。
収束条件から$\Delta t$を決めることもできるとは思いますが、そこまで踏み込めていないため、収束しない場合は$\Delta t$を半分にして再試行する、というイマイチなことをしています。
あとがき
単振り子に対する考察を拡張し、多重振り子に対してのエネルギー保存スキームについて考えてみました。
一応「出来る」ことは示せましたが、重いですしあまり現実的な手法ではないように感じます。
そもそもカオス系なので多少の誤差は飲み込まれてしまいますし、ナイーブな実装でもそれっぽい結果は出ますので、学術的に真面目にやるのでなければ単純なスキームで事足りそうです。
導出自体は他の多自由度の保存系にも適用できると思いますし、非線形で硬めの系に対する一つのアプローチくらいにはなっているかと思います。
