まえがき
単振り子の数値計算例は多く見つかりますが、数値的エネルギー保存性についてはあまり情報を見つけることができなかったため、こちらに記事として残しておきます。
丸め誤差の範囲でエネルギーを保存するスキームの導出と解析結果を主眼とします。
実装は最後に掲載しています。
追記:多重振り子についても考察しました。
TL;DR
文字通り単純な振り子ですがエネルギー保存性よくシミュレートするには一工夫必要です。
ただ陰解法にすればよいというわけでもなく、離散化誤差に注意してスキームを組む必要があります。
問題設定
運動を数値的に解くためにまずは支配方程式を導出します。
鉛直方向に加速度$g$が加えられている二次元空間の原点を中心とする単振り子を考えます。
原点とおもりは長さが$l$で質量の無い剛体棒で繋がっているとします。
力の釣り合いで立式することもできますが、角度を変数とする一自由度の系なので、Lagrangeの式
\frac{d}{dt} \frac{\partial L}{\partial \omega}
-
\frac{\partial L}{\partial \theta}
=
0
を考えます。
おもりの位置ベクトルは$x$軸からの角度を$\theta = \theta \left( t \right)$と置いて
+ \vec{e}_x l \cos \theta + \vec{e}_y l \sin \theta,
速度ベクトルはこの時間全微分
- \vec{e}_x l \omega \sin \theta + \vec{e}_y l \omega \cos \theta
で与えられます。
ここで角速度$\omega \left( t \right)$は
\omega
\equiv
\frac{d\theta}{dt}
です。
したがって運動エネルギー$T \left( \omega \right)$は、速度ベクトルの大きさの二乗が$l^2 \omega^2$であることから
\frac{1}{2} m l^2 \omega^2,
位置エネルギー$U \left( \theta \right)$は鉛直方向の位置から
- m g l \sin \theta
となります。
$m$はおもりの質量です。
なおどこを基準に取るかによって$U$は定数分だけ任意性があります(後述)が、導出の上では微分するため影響はありません。
$g$の符号は一般的な加速度を想定し上向き正で定義しているので、直感的な重力を与える場合には負の値をとります。
Lagrangianを$T - U$で定義していくつか微分を計算すると、Lagrangeの運動方程式は
m l^2 \frac{d \omega}{dt}
-
m g l \cos \theta
=
0
と導かれます。
一方で散逸を一切入れていないので、エネルギーの和(位置エネルギーの性質からハミルトニアンと同値)は保存するはずです。
式で表現すると、全エネルギー$E = T + U$の時間全微分
\frac{dE}{dt}
=
\frac{d}{dt} \left( \frac{1}{2} m l^2 \omega^2 \right)
-
\frac{d}{dt} \left( m g l \sin \theta \right)
が$0$ということです。
若干の計算を行うと、
m l^2 \omega \frac{d \omega}{dt}
-
m g l \omega \cos \theta
=
\omega \left(
m l^2 \frac{d \omega}{dt}
-
m g l \cos \theta
\right)
となり、括弧の中はLagrangeの式から確かに0になります。
座標系について
教科書などでよく見る式と位置エネルギーが違って見えるのは座標系の取り方の違い故です。
一般的には角度を鉛直下向きから測る、つまり$\phi \equiv \theta + \pi / 2$で定義することが多いです。
この場合の支配方程式は
m l^2 \frac{d^2 \phi}{dt^2}
+
m g l \sin \phi
=
0
となり、$\phi$が十分小さいとして線形近似
\sin \phi
\approx
\phi
の下
m l^2 \frac{d^2 \phi}{dt^2}
+
m g l \phi
=
0
とすれば調和振動の解析解が求まるのはお馴染みの話です。
振れ幅が大きい場合はこの近似が妥当ではなくなるため、基本的にコンピュータに投げることになります。
まとめると、支配方程式として以下の連立一階常微分方程式が得られます。
\begin{aligned}
& m l^2 \frac{d\omega}{dt}
-
m g l \cos \theta
=
0, \\
& \frac{d \theta}{dt}
=
\omega.
\end{aligned}
次の章ではこれを数値的に解くことを考えます。
初期条件として$\omega = \theta = 0$を与え、$m = l = -g = 1$とします。
時間刻みは特段表記がなければ$\Delta t = 10^{-2}$とし、$t = 10^2$まで積分することとします。
以下では総エネルギーについて議論しますが、変化量を定量的に表すため正規化の仕方を考える必要があります。
上述の通りポテンシャルエネルギーは定数分だけ任意性がありますので、ここでは初期状態の総エネルギーが$1$、全エネルギーを失って完全に静止した状態が$0$となるように正規化することとします。
一般的なスキーム
最も単純な離散化は速度、角度両方に対してオイラー陽解法(図中でE.-Exp.と表記します)を用いた
\begin{aligned}
& \frac{
\omega^{n+1}
-
\omega^{n }
}{\Delta t}
=
\frac{g}{l} \left( \cos \theta \right)^{n } \\
& \frac{
\theta^{n+1}
-
\theta^{n }
}{\Delta t}
=
\omega^{n }
\end{aligned}
でしょう。
一般に陰解法を用いることで安定性の向上が見込めますので、ここでも適用してみましょう。
速度に対して陰解法を適用するのは少し複雑なので、まずは角度の式に対してだけ適用してみます。
Crank-Nicolson法(図中C.-N.)
\frac{
\theta^{n+1}
-
\theta^{n }
}{\Delta t}
=
\frac{1}{2} \left(
\omega^{n+1}
+
\omega^{n }
\right)
およびオイラー陰解法(図中E.-Imp.)
\frac{
\theta^{n+1}
-
\theta^{n }
}{\Delta t}
=
\omega^{n+1}
を考え、それぞれの場合に対するエネルギーの時間変化を次に示します。
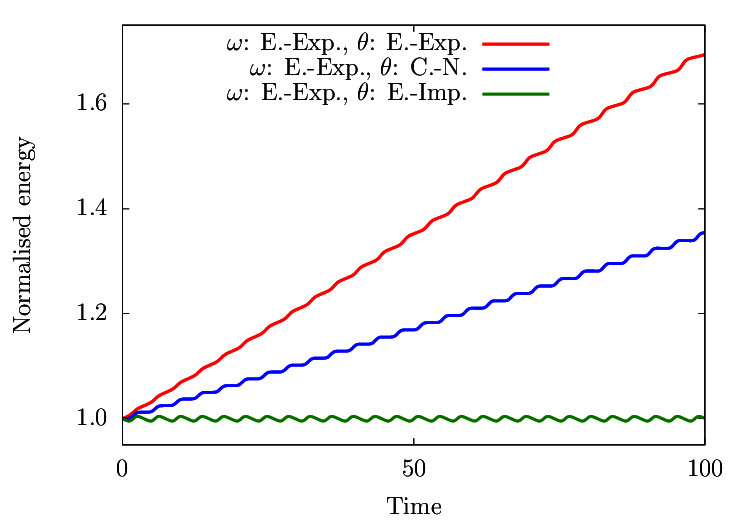
オイラー陽解法を用いた場合、概ね単調増加する傾向が見て取れます。
すなわち振幅が徐々に大きくなっている(100時間単位の積分でエネルギーが50%程度増加する)ということで、これは非物理的であると共に安定性の観点からも好ましくありません。
陰解法を導入した場合、共に完全陽解法に比べ保存性の向上が見られます。
特にオイラー陰解法を用いた場合、1%オーダーの振動は見られるものの、誤差は蓄積しないことが定性的に見て取れます(後述、正準変換)。
これは保存系であるという事実をきちんと反映していると言えますし、統計量を取るために長時間積分する必要がある場合などに好ましい性質です。
角度を更新するためのスキームが保存則に影響を及ぼしうることがわかりましたので、速度に対しても色々と試してみます。
残念ながら$\cos \theta$の項故に非線形の連立方程式となるため、角度の時ほど簡単にはいかず、反復解法が必要になります。
実装は簡単のため収束判定ではなく十分な回数(20回)の反復としています。
全てを示すと冗長なので、代表的なケースのみ示します。
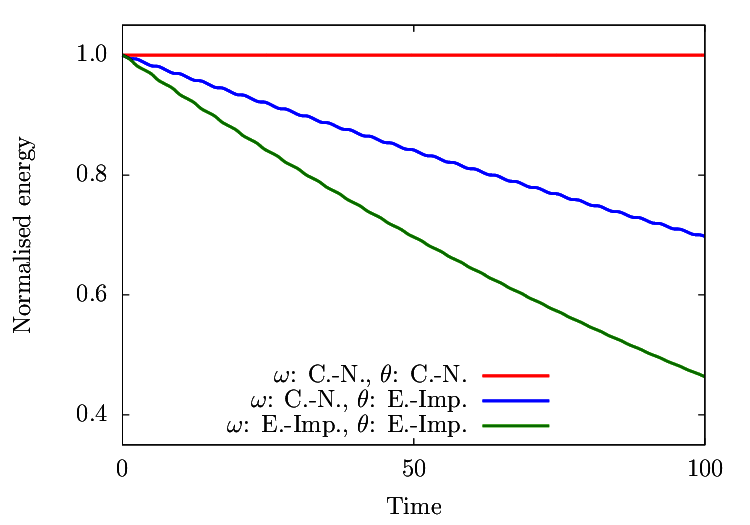
特筆すべきは逆にエネルギーが著しく減少する場合もあるということでしょう。
計算安定性の観点からすれば増加するよりはよほど好ましい性質ですが、散逸がないのに振幅が徐々に小さくなってやがて停止するということで、やはり非物理的であると言えるでしょう。
また角速度と角度の両方にCrank-Nicolson法を適用した赤線の場合、保存性が非常によいことがわかります。
ほぼ直線に見えますが、拡大してみると

実際は$10^{-6}$程度の幅で全エネルギーが増減していることがわかりますが、エネルギー保存性の観点から見れば他の手法に比べて頭一つ抜けているのは確かでしょう。
結果を解釈するとすれば、時間に対して対称のスキームであることと、ニ次精度をもつことが要因と言えるかもしれません。
色々なスキームを用いた結果を示しましたが、全て一次精度以上のスキームですから、刻み幅0の極限で方程式の厳密解(Lagrangeの式)に収束するはずです。
従って刻み幅を十分に小さくすれば(もしくは高精度の差分を用いれば)、Lagrangeの式への追従性とともにエネルギーの保存性も向上するはずなので、そこまで拘る必要はないでしょう。
ただこの記事の対象である単振り子は十分単純ですし、エネルギー保存性に着目してもう少し考えてみようというのが次章の主眼です。
またこの解析が別の記事で多重振り子を考察するための第一歩となります。
エネルギー保存スキーム
導出
数値的に保存性よくLagrangeの式(およびHamiltonの式)を解くというのは解析力学で重視されているテーマのようで、正準変換を元にしたsimplectic積分を用いるアプローチがよく知られているようです。
実際前章で試したスキームのうちいくつかは正準変換となっているはずです。
ただ素人からは若干ハードルが高いと感じたので、ここではもう少し簡単なアプローチを考えてみます。
上で導出した通りLagrangeの式とエネルギー保存式は連続空間では等価ですが、計算結果が示す通り離散空間ではこの性質は保たれませんでした。
すなわちこの二式は離散化されたレベルでは異なっているということです。
この章での目標は、エネルギー保存性をスキームに組み込むことで、丸め誤差の範囲でエネルギーを保存するスキームを構築することです。
この発想を元に、Lagrangeの式ではなくエネルギー保存式
E
=
T + U
=
\frac{1}{2} m l^2 \omega^2
-
m g l \sin \theta
=
const.
を離散化の出発点とします。
この時間微分が0となる、というのは離散的には
\frac{
E^{n+1}
-
E^{n }
}{\Delta t}
=
0
と表現されます。
今後の表記を簡単にするため上のような時間差分を
\frac{\delta E}{\delta t}
などと表記することとします。$n+\frac{1}{2}$における二次精度の中心差分です。
またある量$q$に対する時間平均についても
q^{n+\frac{1}{2}}
\equiv
\frac{
q^{n+1}
+
q^{n }
}{2}
と定義しておきます。これは$n+\frac{1}{2}$における二次精度の補間です。
さて、離散化されたエネルギー保存式の右辺を考えます。
まず運動エネルギーの時間全微分
\frac{\delta T}{\delta t}
=
m l^2 \frac{1}{\Delta t}
\left[
\frac{1}{2}
\left( \omega^{n+1} \right)^2
-
\frac{1}{2}
\left( \omega^{n } \right)^2
\right]
は、大括弧部分が
\frac{
\omega^{n+1}
+
\omega^{n }
}{2}
\left(
\omega^{n+1}
-
\omega^{n }
\right)
より
m l^2 \omega^{n+\frac{1}{2}}
\frac{\delta \omega}{\delta t}
となります。
一方で位置エネルギーの時間全微分
\frac{\delta U}{\delta t}
=
-
m g l \frac{\delta}{\delta t} \left( \sin \theta \right)
に対しては、差分
\frac{1}{\Delta t}
\times
\left[
\sin \left( \theta^{n+\frac{1}{2}} + \frac{\Delta \theta}{2} \right)
-
\sin \left( \theta^{n+\frac{1}{2}} - \frac{\Delta \theta}{2} \right)
\right]
に対して加法定理を用いると、sinc関数
\text{sinc} \left( x \right)
\equiv
\frac{\sin \left( x \right)}{x}
を使って
\frac{2}{\Delta t}
\sin \left( \frac{\Delta \theta}{2} \right)
\cos \left( \theta^{n+\frac{1}{2}} \right)
=
\frac{\Delta \theta}{\Delta t}
\text{sinc} \left( \frac{\Delta \theta}{2} \right)
\cos \left( \theta^{n+\frac{1}{2}} \right)
となります。
ここで
\frac{\Delta \theta}{\Delta t}
=
\omega^{n+\frac{1}{2}}
と中心差分で表現すれば、離散化されたエネルギー保存
\frac{\delta E}{\delta t} = 0
は
\omega^{n+\frac{1}{2}}
\left[
m l^2 \frac{\delta \omega}{\delta t}
-
m g l
\text{sinc} \left( \frac{\Delta \theta}{2} \right)
\cos \left( \theta^{n+\frac{1}{2}} \right)
\right]
=
0
となり、大括弧内が0となることを要求すれば、エネルギー保存性を内包するラグランジュの式
m l^2 \frac{\delta \omega}{\delta t}
-
m g l
\text{sinc} \left( \frac{\Delta \theta}{2} \right)
\cos \left( \theta^{n+\frac{1}{2}} \right)
=
0
が導かれます。
比較のために連続空間での式を再掲します。
m l^2 \frac{d\omega}{dt}
-
m g l \cos \theta
=
0.
第一項は謂わばただ離散化しただけですが、第二項にはsinc関数が含まれます。
これは三角関数の微分関係
\frac{d}{dt} \sin \theta
=
\cos \theta
が、離散化した場合そのままでは成り立たないということです。
なおこの余分に見える項は$\Delta \theta \rightarrow 0$の極限すなわち$\Delta t \rightarrow 0$の極限で$1$なので、確かに元のLagrangeの式
m l^2 \frac{d \omega}{dt}
-
m g l \cos \theta
=
0
に帰着することがわかります。
またsinc関数のTaylor展開から、修正項は$\Delta \theta$に対して二次精度であるとわかるので、Crank-Nicolson法と同程度の収束性を持つことが予想できます(後ほど定量的に示します)。
数値解析
エネルギー保存スキーム
\begin{aligned}
& \frac{
\omega^{n+1}
-
\omega^{n }
}{\Delta t}
=
\frac{g}{l}
\text{sinc} \left( \frac{\theta^{n+1} - \theta^{n }}{2} \right)
\cos \left( \frac{\theta^{n+1} + \theta^{n }}{2} \right), \\
& \frac{
\theta^{n+1}
-
\theta^{n }
}{\Delta t}
=
\frac{1}{2} \left(
\omega^{n+1}
+
\omega^{n }
\right)
\end{aligned}
を用いて計算した場合のエネルギー(1からのズレ)を以下に示します。

倍精度を使用しているので、エネルギーが確かにおおよそ丸め誤差の範囲で保存していることが確認できます。
Crank-Nicolson法との違いを明確にするため、刻み幅を10倍($\Delta t = 10^{-1}$)に大きくして計算した結果も示します。
縦軸は1からのズレを絶対値を取った上で対数表示しています。

二次精度であることからも推測できる通り、Crank-Nicolson法においては振動が$10^{-4}$程度とおよそ元の100倍になっていますが、エネルギー保存スキームでは依然丸め誤差程度を保っています(青線の不連続な部分は誤差が$10^{-16}$以下です)。
解の精度(例えば振り子の周期)は当然刻み幅に依存しますが、スキームの設計を工夫することで保存性を刻み幅に依存しない性質とすることができます。
解の精度についても示しておきます。
エネルギー保存スキームとその他保存はしないものの単調増加や減少を示さなかった二つのスキームの時間刻みに対する収束性を次に示します。
$t = 10$の時点での$\theta$の値を対象とし、誤差$\epsilon$をRichardson extrapolationによって得られる擬似的な理論解からのズレと定義しています。
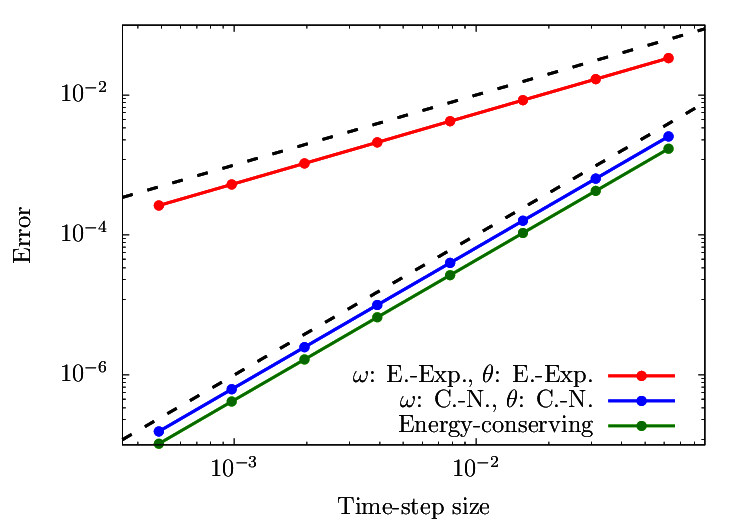
予想どおり、オイラー法を適用したものは一次、その他(Crank-Nicolsonおよびエネルギー保存スキーム)は二次の精度を示します。
実装
コードはこちらにおいてあります。
上で取り上げた様々な組み合わせをkernelとして個々で実装し、積分する関数integrateに渡しています。
あとがき
単振り子に対するエネルギー保存性の高いスキームについて考えてみました。
通常のやり方でエネルギー保存が破られてしまう理由は、$\sin \theta$の差分が$\cos \theta$にはならないためでした。
ただし細かいことに拘らなくてもある程度の誤差で保存則を満たすスキームは簡単に組めますし、どれも$\Delta t \rightarrow 0$できちんと理論解に収束します。
よって単振り子に関してはそれほど大きな差はないと言ってもよいと思います。
またエネルギー自体が保存しない場合でも、正準変換を満たすスキームであれば擬似的な量$E + \Delta E$が保存し、誤差は刻み幅の関数となってある程度に抑えられるようです(謝辞参照)。
なにはともあれ離散化誤差が入りうる一つのケースの紹介と受け止めていただければと思います。
謝辞
正準変換と保存性については神戸大学の陰山聡先生のノートを参考にさせていただきました。
素晴らしい資料を公開してくださっていることを感謝いたします。