これは何?
を読んで、多項式でやるとどうなるかを試したくなったので書いた。
なにかというと、値の異なる定数関数を滑らかにつなぎたいという話。
元の記事はシグモイド曲線を加工していたけど、多項式も悪くないよと思って。
設定
話を簡単にするため、
F(x)=\left\{
\begin{array}{ll}
-1 & if \: x≦-1 \\
f(x) & if\:-1<x<1 \\
1 & if \: 1≦x \\
\end{array}
\right.
という設定にする。
小文字の方の $ f(x) $ を多項式にする。
f(x) が満たすべき性質
満たすべき性質として必須なのはまず連続性。
- $f(-1)=-1$
- $f(1)=1$
それと
- $f(-x)=-f(x)$
だと使いやすそうなのでこの性質も入れておく。
あとは適当に $n$ を定めて $0<i≦n$ のとき、$x=±1$ における $n$ 階微分がゼロになればいい。
そうすれば $F(x)$ は $n$ 階微分まで連続になる。
そういう関数は無限にあるが、そういう性質を満たす多項式で最低次数のものとなると一意に定まる。
1階微分まで 〜 6階微分まで のグラフ
対称性から偶数次の項がなくなる。
あとはふつうに方程式
\begin{align}
f(1) &= 1 \\
\frac{d^i}{dx^i}f(1) &= 0 \: \: \: \: if \: \: \: \: i ∈ \{1, 2, ..., n \}
\end{align}
を解けばよい。
解いた結果が以下。
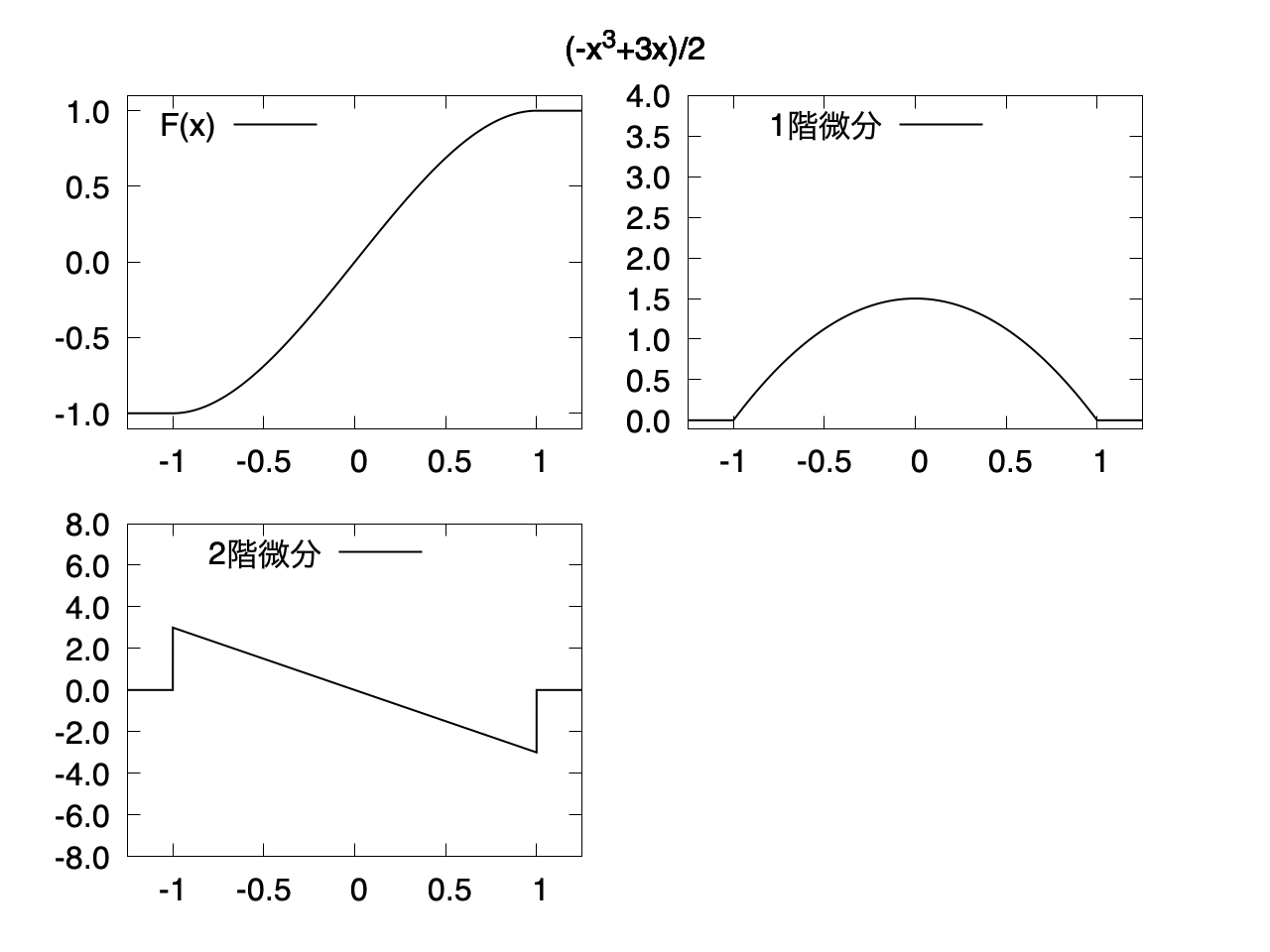
1階微分まで連続
$f(x)$ は 3次関数になる。
$F(x)$ は 2階微分が不連続になる。
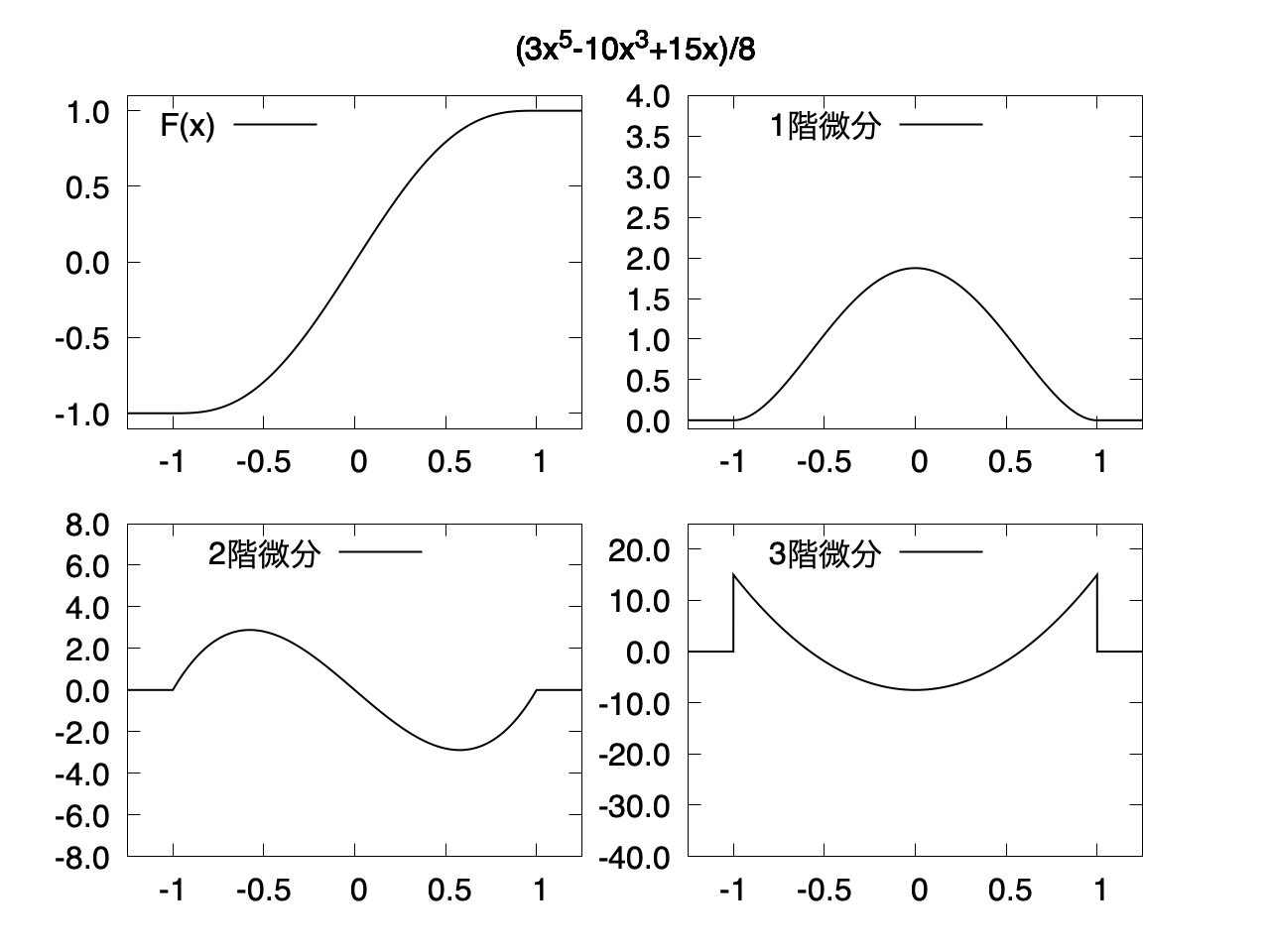
2階微分まで連続
$f(x)$ は 5次関数になる。
$F(x)$ は 3階微分が不連続になる。
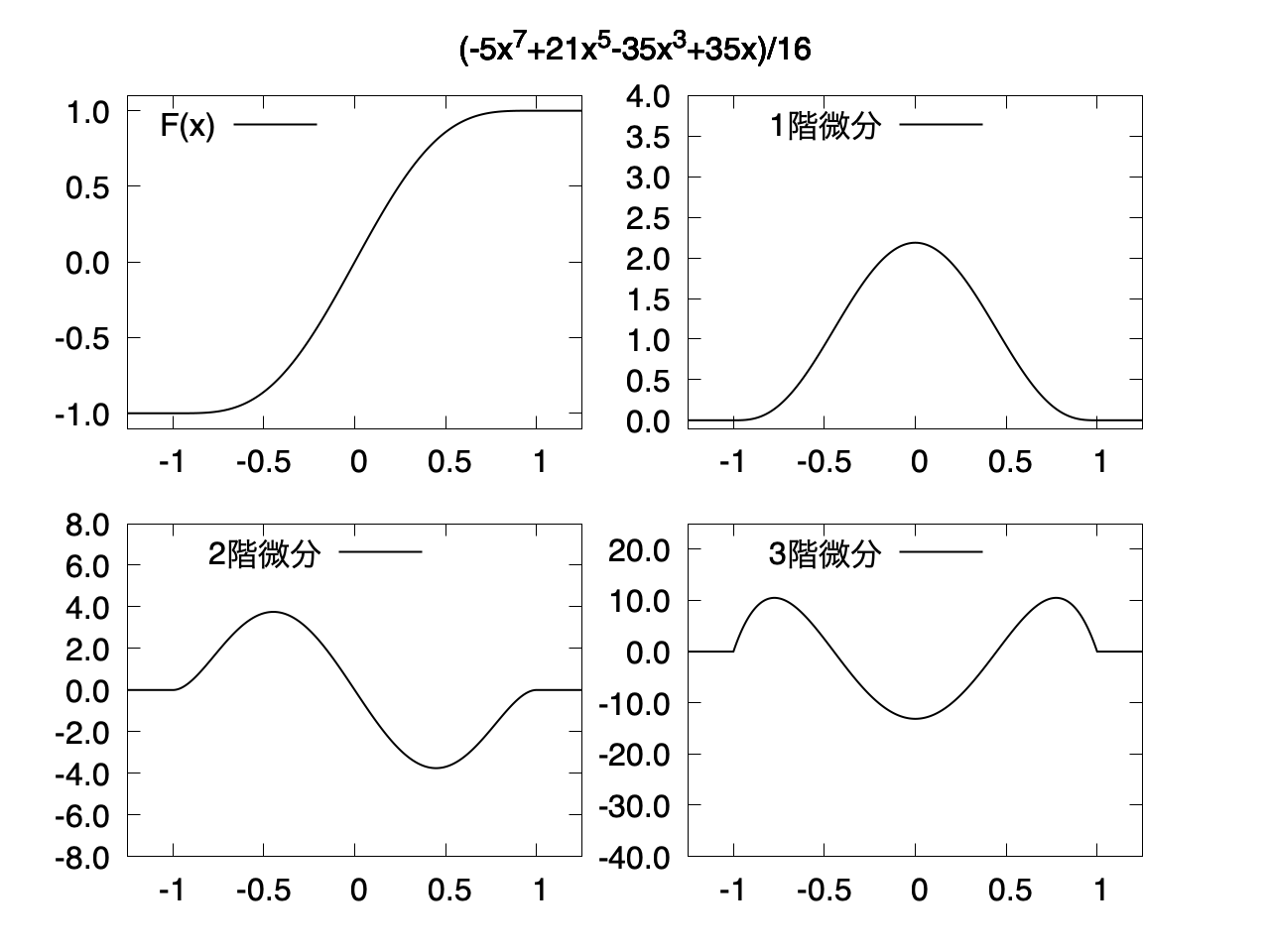
3階微分まで連続
$f(x)$ は 7次関数になる。
$F(x)$ は 3階微分に微分不可能な点がある。
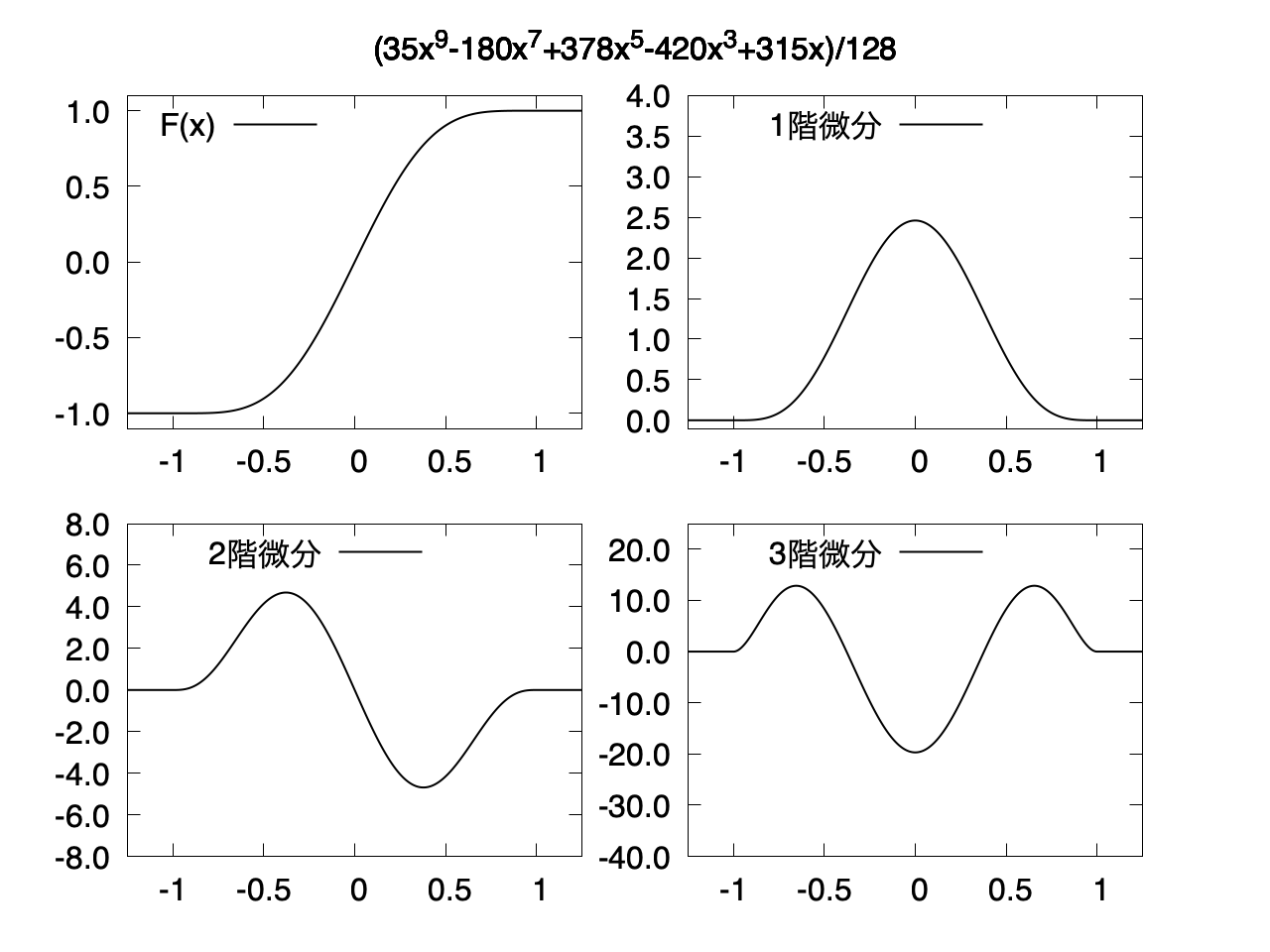
4階微分まで連続
$f(x)$ は 9次関数になる。
$F(x)$ は 3階微分もなめらか。
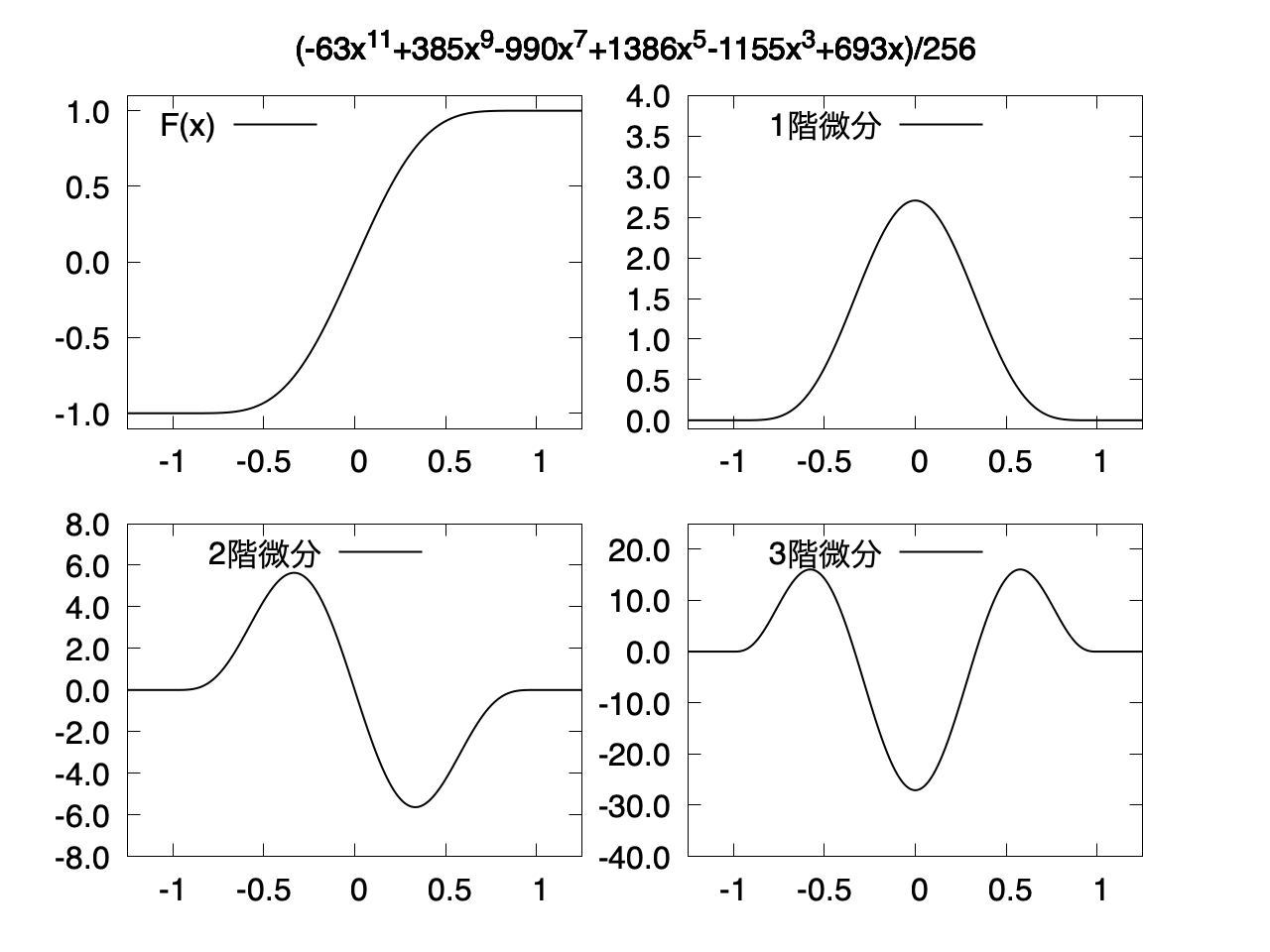
5階微分まで連続
$f(x)$ は 11次関数になる。
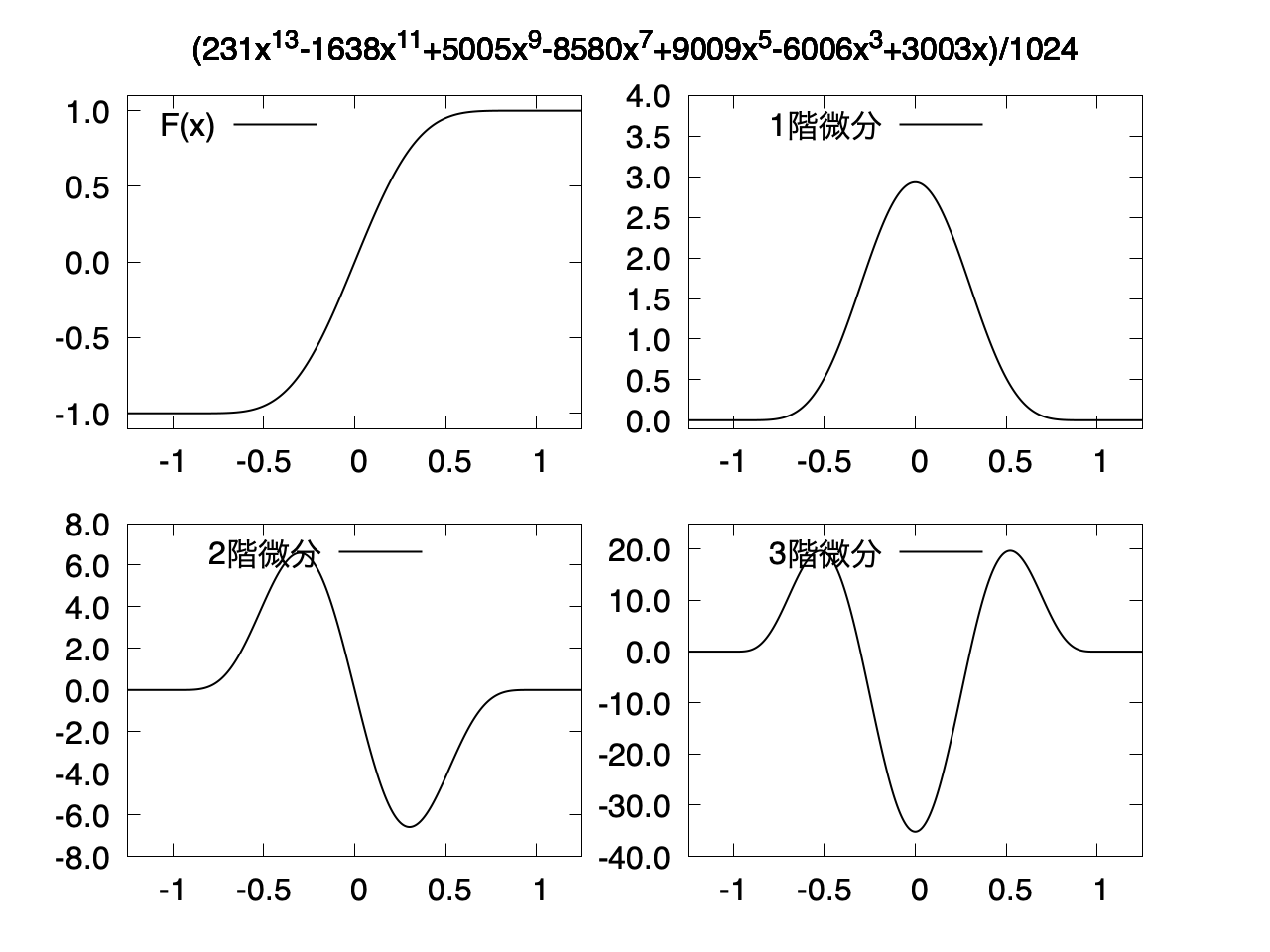
6階微分まで連続
$f(x)$ は 13次関数になる。
元の記事の計算
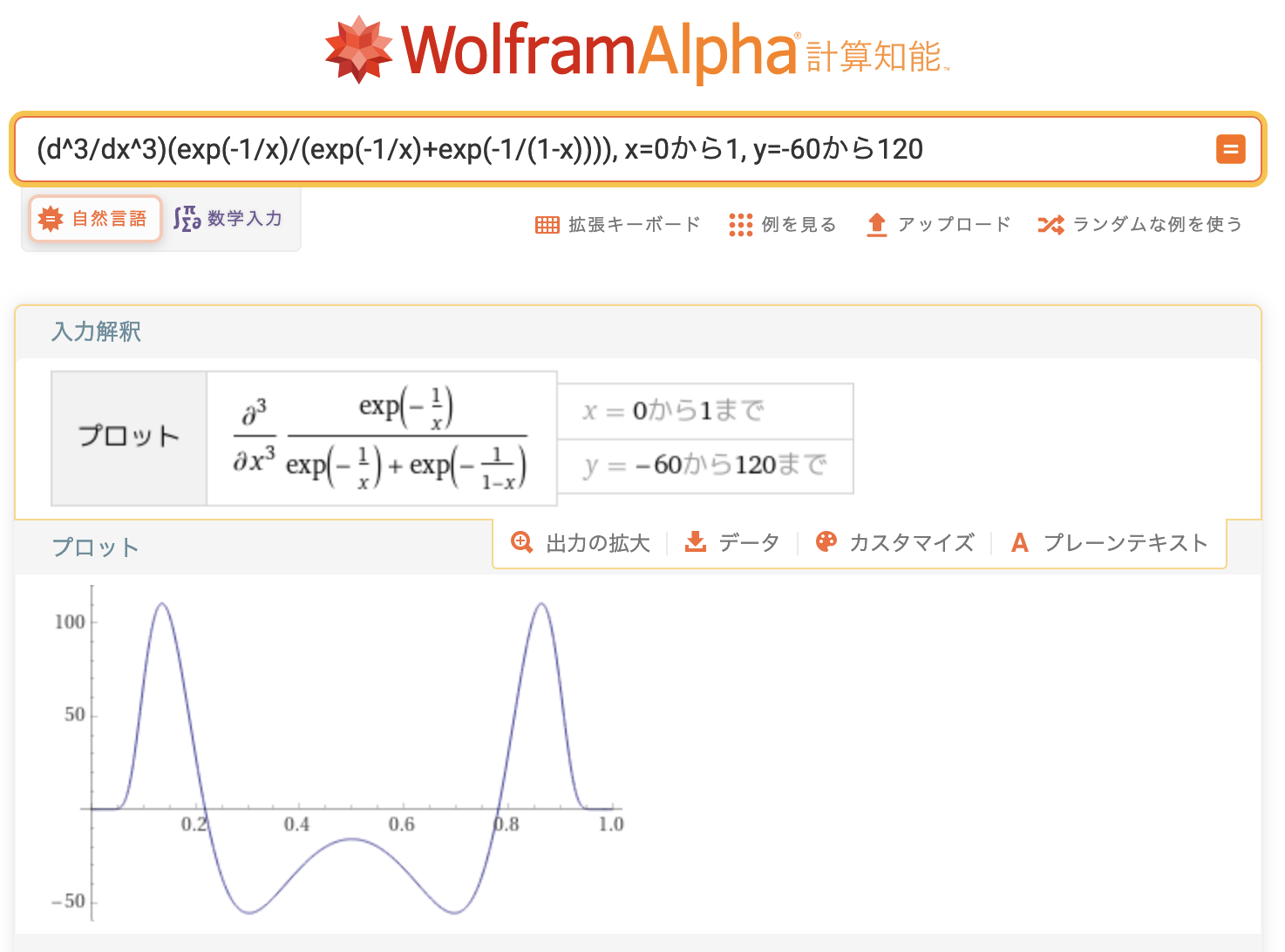
3階微分すると
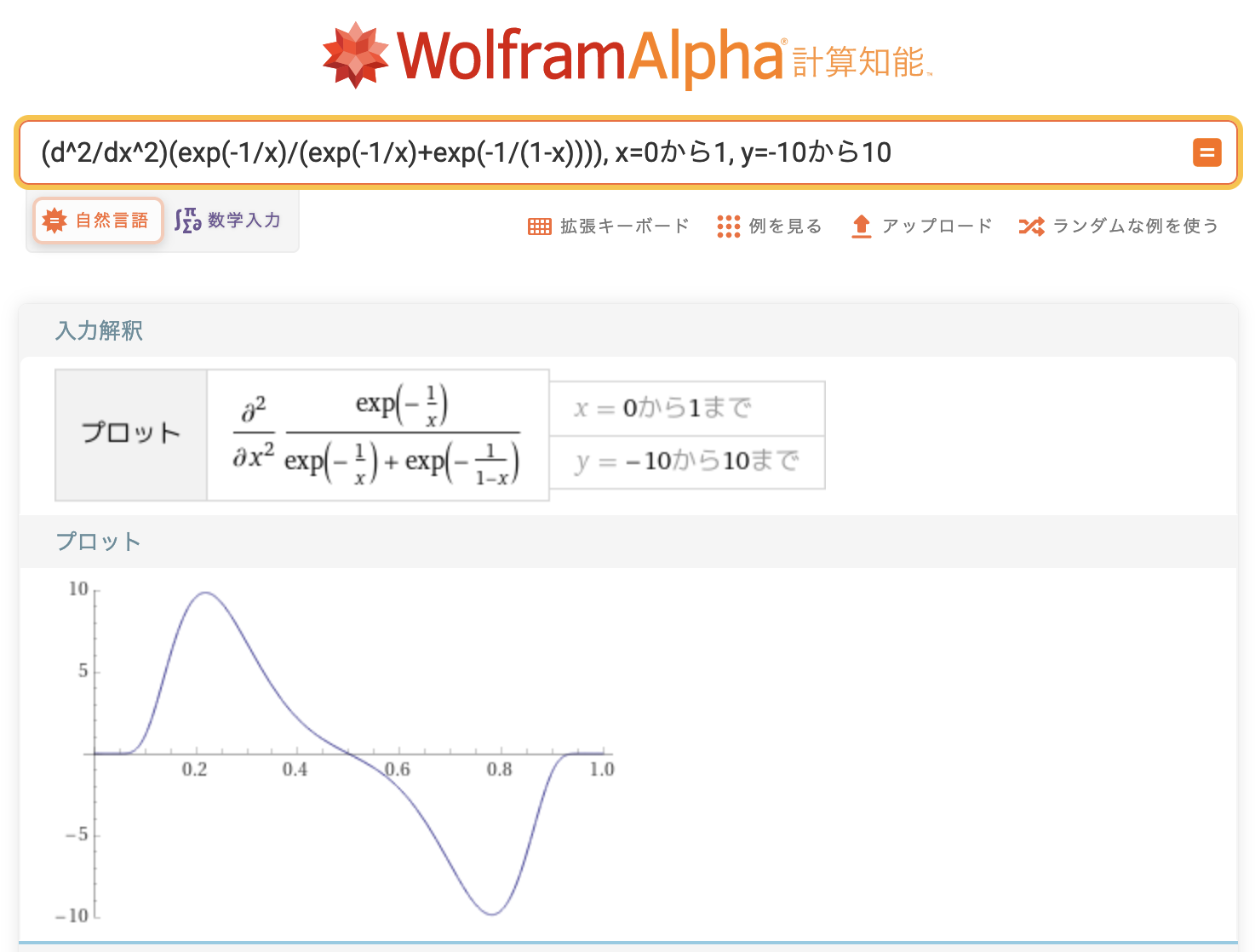
こんな恐ろしいことになってしまうので、WolframAlpha 様に全部お願いした。
プロットして初めてわかったけど、2階微分の変曲点が多項式版より多い。
1階微分
2階微分
3階微分
まとめと感想
私から見える用途だと、3階微分まで連続、までは使いみちがありそう。
計算すると 10階でも20階でもいけるけど、そうなってくると工夫して計算しないと誤差が溜まって大変なことになるので要注意。
あと。
最初は python + matplotlib で書こうかと思ってたけど、 ruby + gnuplot で書いた。
ruby 好きなのでこっちが楽。
ソースコードは以下。100行足らず。
require "matrix"
def exptext(ks,c)
d = ks.inject(1){ |acc,e| acc.lcm(e.denominator) }
m = ks.zip(c).reverse.map{ |k,e|
ex = e==1 ? "" : "^{#{e}}"
ks = k*d==1 ? "" : (k*d==-1 ? "-" : "%+d" % (k*d).to_i )
"#{ks}x#{ex}"
}.join
m.gsub!( /^\+/, "" )
d==1 ? m : "(#{m})/#{d}"
end
def con(n)
c=(0...n).map{ |e| e*2+1 }
m=Matrix[*c.map.with_index(0){ |e,ix|
if ix==0
[1]*c.size
else
c.map{ |e| ((e-ix+1)..e).inject(&:*) }
end
}]
v = Matrix[ [1]+[0]*(c.size-1) ].transpose
ks=(m.inv*v).to_a.flatten
[
exptext(ks,c),
ks.zip(c).map{ |k,e| "#{k.to_f}*x**#{e}" }.join("+"),
ks.zip(c).map{ |k,e| "#{(k*e).to_f}*x**#{e-1}" }.join("+"),
ks.zip(c).map{ |k,e| "#{(k*e*(e-1)).to_f}*x**#{[0,e-2].max}" }.join("+"),
ks.zip(c).map{ |k,e| "#{(k*e*(e-1)*(e-2)).to_f}*x**#{[0,e-3].max}" }.join("+"),
]
end
def init_plot(n)
[
"set term pngcairo size 1280, 960 font ',24'",
"set sample 10000",
"set output 'graph#{n}.png'",
"set key left top",
"set format y '%5.1f'",
]
end
def g(n)
exp, y, dy, ddy, dddy = con(n)
xrange = "[-1.25:1.25]"
with="with lines lw 2 lc black"
s = [
*init_plot(n),
"set label 1 center at screen 0.5,0.95 '#{exp}'",
"set xrange #{xrange}",
"set multiplot layout 2,2 margins 0.1,0.9,0.1,0.9 spacing char 6,3",
"set yrange [-1.1:1.1]",
"plot x<-1 ? -1 : (1<x ? 1 : #{y}) #{with} title 'F(x)'",
"set yrange [-0.1:4]",
"plot x<-1 ? 0 : (1<x ? 0 : #{dy}) #{with} title '1階微分'",
]
if 1<n
s+=[
"set yrange [-8:8]",
"plot x<-1 ? 0 : (1<x ? 0 : #{ddy}) #{with} title '2階微分'",
]
end
if 2<n
s+=[
"set yrange [-40:25]",
"plot x<-1 ? 0 : (1<x ? 0 : #{dddy}) #{with} title '3階微分'",
]
end
puts %x!echo "#{s.join("\n")}" | gnuplot -!
end
[1,2,3,4,5,6,7].each do |x|
g(x)
end