ゼロからはじめるmatplotlib〜2.関数のグラフ化〜

ゼロからはじめるmatplotlib〜1.点のプロットと軸の調節〜
前回は座標上の点のplotの仕方について書きました。

今回は、点ではなく点を細かく繋いで関数のplotをします。

関数のplotの流れ

1step

表示したい関数の定義域をnp.arange()を使ってリストとして作成する。

例)x=np.arange(-5,5,0.1)```
↓
**2step**
```1stepで作ったリストに対して表示したい関数を適用する。
例)y=x**2```

**3step**
```plt.plot(x,y)を実行。```

この3stepで簡単に関数を作成することができます。

## 準備
まずは前回同様matplotlibを呼び出すおまじない「ウィンガーディアムレビオーサ」。

```py
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

使用する2つのメソッドの説明

####1.plt.plot(x, y)
xとyにリストを渡すと、点同士が直線で繋がれます。
例えば、

plt.plot([1,2,3,4],[1,7,3,5])

とすると(1,1)→(2,7)→(3,3)→(4,5)の点がこの順に直線で結ばれます。

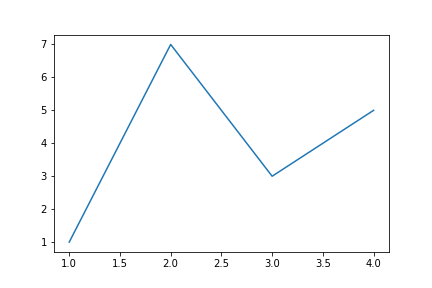
この時、plotはリスト内の順番通りに結ばれていくことに注意してください。

2.np.arange(初めの数, 終わりの数+1, 何個ずつ増えるか)

np.arangeはある範囲の等差数列のnumpy arrayを作成することができます。
(初めの数=0, 終わりの数+1=10, 1ずつ増加）と設定して実行。

np.arange(0, 10, 1)

<実行結果>

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

実際に関数を表示させてみる。

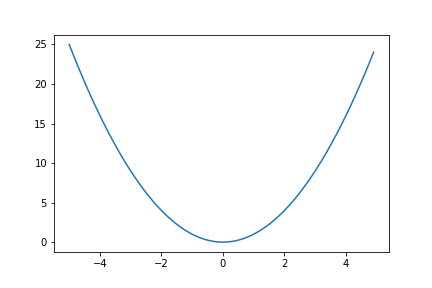
2次関数 $y=x^2$を $(-5 \leqq x < 5)$ の範囲でplotしてみます。

# 1step:x軸の点を-5から５まで0.1刻みで生成
x = np.arange(-5, 5, 0.1)
# 2step:上のリストに対して関数を適用
y = x**2
# 3step:plt.plot(x軸を指定, y軸を指定)
plt.plot(x,y)

#これは表示の時のおまじない(jupyter上では書かなくても表示される。)
plt.show()

＜実行結果＞

どのように関数が表示されているか。

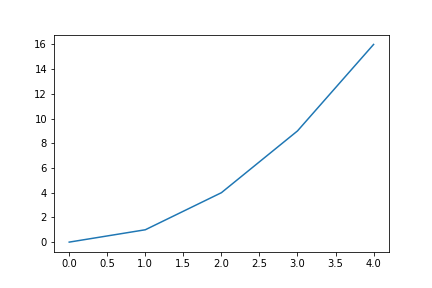
xを1刻みにしてみると曲線が表示されません。

x = np.array([0,1,2,3,4])
y = x**2
plt.plot(x, y)

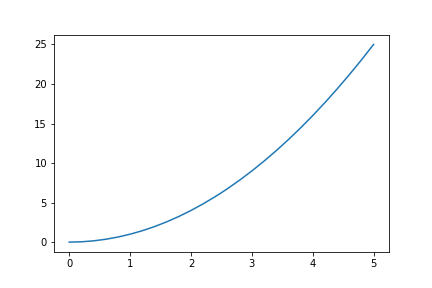
xの幅を細かくすると、、

x = np.array([0, 0.2 ,0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0,
              2.2, 2.4, 2.5 ,2.6 ,2.8 ,3.0 ,3.2 ,3.4 ,3.6 ,3.8 ,4.0,
              4.2, 4.4, 4.6, 4.8 ,5.0])
y = x**2
plt.plot(x, y)

このように、 生成するX軸の点を細かくすることでなめらかな曲線として表示することができます。
np.arangeとplt.plotを組み合わせることでグラフを簡単に作ることができます。

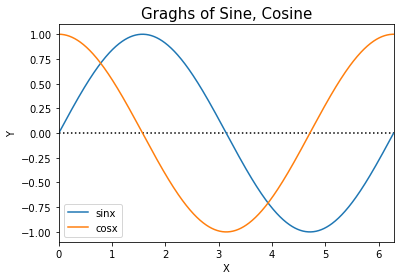
前回と今回学んだことを組み合わてsin,cos曲線の表示

# 1step
x = np.arange(0,2*np.pi,0.01)
# 2&3step
# label=でラベル指定して、あとでplt.legend()を加えた時に凡例が表示されるようにしています。
plt.plot(x, np.sin(x), label="sinx")
plt.plot(x, np.cos(x), label="cosx")

# 前回の軸の調節やタイトルの調節など
plt.xlim(0, 2*np.pi)
plt.hlines(0 ,0 , 2*np.pi, "k", linestyle=":")
plt.title('Graghs of Sine, Cosine',fontsize=15)
plt.xlabel('X',fontsize=10)
plt.ylabel('Y',fontsize=10)
plt.legend()
plt.show()

<出力結果>

間違えがちなこと

plt.plot([2,1,4,3],[7,1,5,3])

とするとソートされないので(2,7),(1,1),(4,5),(3,3)の順に直線で結ばれます。

下のように書くと出力されません。(numpy arrayではなくlist形式なので、、、)

x = [0,1,2,3,4]
y = x**2
plt.plot(x, y)

まとめ

1step

表示したい関数の定義域をnp.arange()を使ってリストとして作成する。

例)x=np.arange(-5,5,0.1)```
↓
**2step**
```1stepで作ったリストに対して表示したい関数を適用する。
例)y=x**2```

**3step**
```plt.plot(x,y)を実行。```

この3stepで簡単に関数を作成することができます。

今回は曲線のplotについてやりました。
色々な関数を表示させながら仕組みをつかんでいきましょう！