この記事はStan Advent Calenderの18日目の記事です。間違っているところや改善点などご指摘いただければ幸いです。
アニメに関するキャプチャ画像は、本稿内容の紹介に必要最低限な範囲で使用するものとして利用させていただきます。
動作環境:Windows, R3.3.1,Rstan2.11.1
みなさんこんにちは。寒い季節になりましたね。
今回はStanアドカレでも (一部で) 話題になっている、みんな大好きラブライブ!のお話です。
ラブライブとは:『ラブライブ! School idol project』(ラブライブ スクールアイドルプロジェクト、通称:ラブライブ)は国立音ノ木坂学院で結成された架空のアイドルグループの奮闘と成長を描く日本のメディアミックス作品群 (アンサイクロペディアより)。
そんなラブライブの人気は衰えるところを知らず、アニメが終わった今もリズムゲームのアーケード版が全国のゲームセンターで好評稼働中らしいですよ!みんなお金持ってゲームセンターへ急ぎましょう!
さてさて本稿ではそんなラブライブに登場する9人の女の子に対する選好と選択した人物の個人特性の関連に関して、Stanによる多項ロジスティック回帰分析を用いてベイズ推定してみました。
研究の背景その1
私は友達に連れられて、このアニメに出てくるにこちゃんとよばれる子を初めて見たときに思いました。

「あ、これは好きになるわ」
と。
案の定、アニメの中に彼女が出てきて2分後くらいにはすぐに[にこ推し]になりました。
無理もないことです。かわいいですから。
ですが、ラブライブに出てくるキャラクター(以下、彼女たちのユニット名であるμ'sとします)は、いずれもとてもかわいい子ばかりです。
そんなμ'sの中で、誰を推すかというキャラクターの選択に外向性や神経症傾向などのパーソナリティ特性がどのようにかかわっているのでしょうか。
これがわかると、**「あなたはμ'sの中のだれ推しですか?」という質問がそのまま「あなたはどういったパーソナリティをお持ちですか?」**という質問に生まれ変わるのだ!これはすごい!意義に対する疑念の余地はない!
これまでの心理学的領域で、もっとも知見の積み重ねられたパーソナリティの特性論であるビッグファイブは、人間の持つ特性を5つの因子で説明しています。その5つの因子とは、「経験への開放性(O)」「誠実性(C)」「外向性(E)」「協調性(A)」「神経症傾向(N)」です。
私はそこそこ経験に開放的おじさんなので、
「にこちゃんを好きな人は経験に開放的おじさんである」
という大胆な仮説を立てて、以下の分析を行っていきます。
研究の背景その2
Google drive使ったネット調査をしてみたかった+実データを用いた多項ロジスティック回帰をベイズでしてみたかったんです。。。
多項ロジスティック回帰とは
K 種類 (ここではμ'sの数:9人) の名義尺度による目的変数 $y_n$ (誰を選択するか) が、 D 次元の説明変数 $x_n$ (ここでいうBig Fiveや性別など) により予測される回帰式である。後のコードに出てくるSoftmax関数の定義についてはStan Reference Manualの386p辺りをご参照ください。ソフトマックス回帰と呼ばれることもあります。
この回帰分析では回帰係数が不確実性を持つため、一つの参照カテゴリー $r$ に $0$ の定数を置くことで相対的な解釈を可能にします。 $r$ に関して、 $β_D = 0$ ですね。詳しくは犬4匹本なりググるなりしてください。今回の参照カテゴリーには、主人公である穂乃果ちゃんを選択しています。
方法
参加者 SNS(twitter, line)などを通して収集した92名 (男44人、女48人) の参加者(ご協力いただいた皆様本当にありがとうございます!!
質問紙 日本語版Ten Item Personality Inventory(TIPI-J:小塩他, 2012)の質問紙10項目を使用。Big Fiveを測定する質問紙。
手続き 参加者にはGoogle formにて回答をしてもらった。まず年齢、性別を回答してもらい、その次にTIPI-J、最後に μ’s 9人が移ったポスターの中から一人だけ好みの女の子を選択してもらった。
結果1. まずは選挙からはじめよう。
まずは最も得票数が多かったのは誰なのか。
Rstanユーザーなら無駄に事後分布で報告しようじゃありませんか。
以下はくっそ単純に選択率を算出したStanコードです。
(事後分布の差分を比較しようかと思いましたが、数が多くて面倒だったので分布見てどうぞって感じにしてます。
※12/20二項分布で出してましたが、多項分布で算出するコードに変更いたしました。
data{
int K; //変数の数
int D[K]; //生起数
}
parameters{
simplex[K] theta;
}
model{
D ~ multinomial(theta);
}
ほんでRコードは以下の通りです。
# museの話
d <- read.table("clipboard",header=T)
# 合計得点の作成 ここの無駄感半端ないです。
d <- mutate(d,Ex = 0)
d <- mutate(d,Ag = 0)
d <- mutate(d,Co = 0)
d <- mutate(d,Ne = 0)
d <- mutate(d,Op = 0)
foreach(i = 1:nrow(d)) %do% {
d[i,14] <- sum(d[i,3]+8-d[i,8])
d[i,15] <- sum(d[i,4]+8-d[i,9])
d[i,16] <- sum(d[i,5]+8-d[i,10])
d[i,17] <- sum(d[i,6]+8-d[i,11])
d[i,18] <- sum(d[i,7]+8-d[i,12])
}
# 数を数える
m_n <- matrix(0,9,1)
foreach(i = 1:9)%do%{
m_n[i,] <- as.integer(sum(d[,13] == i))
}
bimodel <- stan_model(file='bino.stan')
fit <- sampling(bimodel,data=list(K=9, D=m_n[,1]),iter=5000)
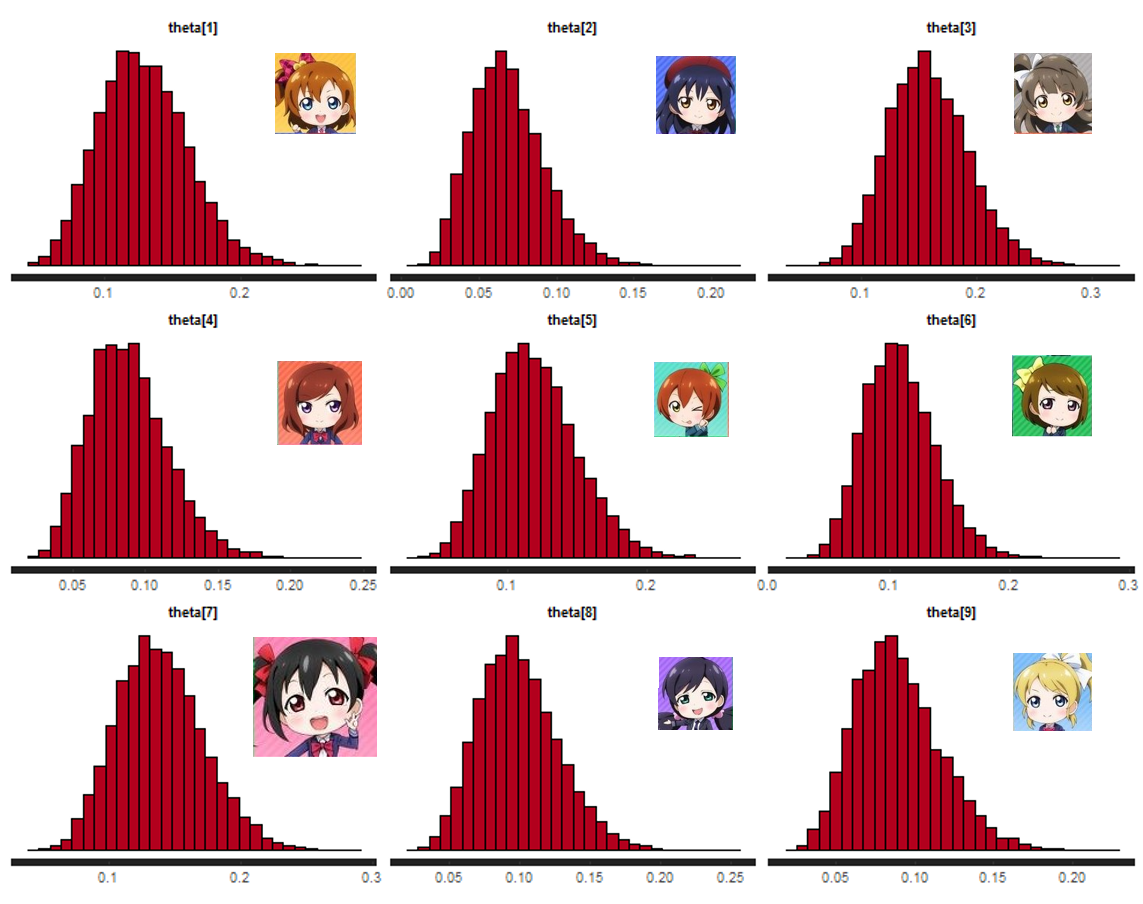
stan_hist(fit,pars=c("theta"))
ちなみにこのStanコードは単純すぎて、MCMC(*´Д`)ハアハアとうち終わるころには解析が終了します。
その結果が以下です。どどん。
4 chains, each with iter=5000; warmup=2500; thin=1;
post-warmup draws per chain=2500, total post-warmup draws=10000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta[Hon] 0.13 0.00 0.03 0.07 0.11 0.13 0.15 0.20 9373 1
theta[Umi] 0.07 0.00 0.02 0.03 0.05 0.07 0.08 0.12 8832 1
theta[Kot] 0.16 0.00 0.03 0.10 0.13 0.16 0.18 0.23 8972 1
theta[Mak] 0.09 0.00 0.03 0.04 0.07 0.09 0.11 0.15 8996 1
theta[Rin] 0.12 0.00 0.03 0.07 0.10 0.12 0.14 0.19 9289 1
theta[Han] 0.11 0.00 0.03 0.06 0.09 0.11 0.13 0.17 8948 1
theta[Nic] 0.14 0.00 0.03 0.08 0.12 0.14 0.16 0.21 8381 1
theta[Noz] 0.10 0.00 0.03 0.05 0.08 0.10 0.12 0.16 9182 1
theta[Eli] 0.09 0.00 0.03 0.04 0.07 0.09 0.11 0.15 8748 1
海未ちゃん (上段左) が0.07中心で若干低いくらいで、他は大体0.1かそれ以上で大差ない感じですね。
ちなみにトップはことりちゃん (上段真ん中) ですが、2位は我らがにこちゃん (中段右) のようですね。
まぁにこちゃんはかわいいですから。しょうがないですね。
ことにこですね。
とはいえ、さすが μ's 。平等に愛されてるんですね (海未ちゃんには目を逸らしながら)。
結果2.どんなやつがどのスクールアイドルを選択しちゃうんだろう
さてお待ちかね、本稿のメインである個人特性とキャラクター選好に関する推定です。
K-1の設定がStan Reference Manual見てもうまく回らんくて苦戦しましたが、なんとかなりました。
Stanコードは以下の通り。
data {
int<lower=1> N; // サンプルサイズ
int<lower=1> P; // 説明変数の数
int<lower=1> K; // ターゲットカテゴリー数:9人や、ウチを入れて!
int<lower=1, upper=K> y[N]; // 目的変数
vector[P] x[N]; // 説明変数
}
parameters {
matrix[K-1, P] beta_raw;
}
transformed parameters {
matrix[K, P] beta; // K-1 handling
// beta K-1 handling
for (k in 1:(K-1))
beta[k] = beta_raw[k];
beta = append_row(beta_raw, rep_row_vector(0, P)); //0を頑張って作って合体させる
}
model {
for (k in 1:(K-1))
beta_raw[k] ~ normal(0, 5);
for (i in 1:N)
y[i] ~ categorical(softmax(beta * x[i])); // categorical_logitでも代用可能
}
ほんでRコードは以下の通りです。
# K-1!!できた!!
Kmodel <- stan_model(file='simple_mlogi.stan')
fit2 <- sampling(Kmodel,data=list(N=nrow(d), P=7, K=9, y=d$muse,
x=cbind(rep(1,nrow(d)),((d[,14:18])/14),(d[,2]))),iter=5000)
print(fit2,pars=c("beta"))
その結果が以下です。
※B = 切片、Ex = 外向性、Ag = 協調性、Co = 勤勉性、Ne = 神経症傾向、Op = 経験への開放、sex = 性別 (0 = 女, 1 = 男)の回帰係数
4 chains, each with iter=5000; warmup=2500; thin=1;
post-warmup draws per chain=2500, total post-warmup draws=10000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta[Umi,B ] 0.25 0.02 2.38 -4.55 -1.32 0.28 1.90 4.74 10000 1
beta[Umi,Ex] -2.07 0.02 2.49 -7.13 -3.71 -2.00 -0.35 2.62 10000 1
beta[Umi,Ag] -0.79 0.03 2.98 -6.84 -2.78 -0.75 1.25 4.92 10000 1
beta[Umi,Co] -0.39 0.02 2.50 -5.40 -2.05 -0.36 1.29 4.37 10000 1
beta[Umi,Ne] -0.75 0.02 2.31 -5.23 -2.33 -0.76 0.82 3.80 10000 1
beta[Umi,Op] 0.40 0.02 2.49 -4.47 -1.24 0.41 2.07 5.23 10000 1
beta[Umi,sex] 0.91 0.01 1.13 -1.23 0.15 0.88 1.63 3.23 10000 1
beta[Kot,B ] -1.06 0.02 1.98 -4.92 -2.39 -1.05 0.25 2.84 7798 1
beta[Kot,Ex] 2.31 0.02 1.93 -1.43 1.00 2.27 3.62 6.12 10000 1
beta[Kot,Ag] 2.42 0.02 2.14 -1.74 0.99 2.41 3.84 6.62 10000 1
beta[Kot,Co] -0.71 0.02 2.00 -4.61 -2.06 -0.67 0.66 3.13 10000 1
beta[Kot,Ne] -0.22 0.02 1.78 -3.76 -1.40 -0.22 0.95 3.29 10000 1
beta[Kot,Op] 0.00 0.02 1.98 -3.82 -1.33 0.01 1.36 3.89 10000 1
beta[Kot,sex] -2.28 0.01 1.03 -4.41 -2.94 -2.23 -1.58 -0.38 10000 1
beta[Mak,B ] -0.48 0.02 2.28 -4.99 -1.99 -0.47 1.03 4.03 10000 1
beta[Mak,Ex] 3.00 0.02 2.21 -1.24 1.47 2.99 4.52 7.39 10000 1
beta[Mak,Ag] -0.82 0.03 2.82 -6.52 -2.67 -0.78 1.06 4.66 10000 1
beta[Mak,Co] -1.21 0.02 2.37 -5.94 -2.79 -1.19 0.41 3.34 10000 1
beta[Mak,Ne] -0.17 0.02 2.10 -4.27 -1.59 -0.16 1.23 3.91 10000 1
beta[Mak,Op] -3.15 0.02 2.31 -7.74 -4.66 -3.15 -1.62 1.36 10000 1
beta[Mak,sex] 1.27 0.01 1.08 -0.76 0.55 1.25 1.96 3.50 10000 1
beta[Rin,B ] -0.93 0.02 2.13 -5.14 -2.35 -0.88 0.52 3.10 10000 1
beta[Rin,Ex] -0.08 0.02 2.02 -4.03 -1.45 -0.08 1.30 3.90 10000 1
beta[Rin,Ag] -0.29 0.02 2.45 -5.09 -1.98 -0.26 1.41 4.39 10000 1
beta[Rin,Co] -2.49 0.02 2.18 -6.80 -3.98 -2.47 -1.00 1.68 10000 1
beta[Rin,Ne] 2.15 0.02 1.97 -1.65 0.81 2.08 3.45 6.04 10000 1
beta[Rin,Op] 0.33 0.02 2.15 -3.88 -1.14 0.33 1.77 4.54 10000 1
beta[Rin,sex] 0.71 0.01 0.88 -0.99 0.12 0.71 1.29 2.48 10000 1
beta[Han,B ] -0.52 0.02 2.20 -4.97 -1.98 -0.51 0.96 3.79 8158 1
beta[Han,Ex] -2.14 0.02 2.20 -6.50 -3.62 -2.10 -0.62 2.03 10000 1
beta[Han,Ag] 1.55 0.02 2.42 -3.20 -0.08 1.58 3.20 6.28 10000 1
beta[Han,Co] -0.20 0.02 2.27 -4.71 -1.74 -0.16 1.32 4.24 10000 1
beta[Han,Ne] 1.64 0.02 2.03 -2.25 0.25 1.64 3.02 5.60 10000 1
beta[Han,Op] -0.46 0.02 2.23 -4.86 -1.95 -0.45 1.06 3.89 10000 1
beta[Han,sex] -0.28 0.01 0.92 -2.11 -0.89 -0.26 0.35 1.50 10000 1
beta[Nic,B ] -0.57 0.02 1.98 -4.51 -1.89 -0.57 0.78 3.23 7671 1
beta[Nic,Ex] 1.45 0.02 1.91 -2.28 0.16 1.44 2.72 5.23 10000 1
beta[Nic,Ag] 1.48 0.02 2.27 -3.01 -0.05 1.50 3.01 5.89 10000 1
beta[Nic,Co] -1.81 0.02 2.03 -5.86 -3.17 -1.80 -0.44 2.13 10000 1
beta[Nic,Ne] -0.03 0.02 1.82 -3.66 -1.24 -0.01 1.20 3.54 10000 1
beta[Nic,Op] -0.22 0.02 2.01 -4.20 -1.55 -0.21 1.14 3.63 10000 1
beta[Nic,sex] 0.14 0.01 0.85 -1.48 -0.42 0.13 0.70 1.83 10000 1
beta[Noz,B ] -2.61 0.03 2.31 -7.32 -4.10 -2.55 -1.04 1.79 8006 1
beta[Noz,Ex] -2.07 0.02 2.28 -6.68 -3.57 -2.00 -0.52 2.29 10000 1
beta[Noz,Ag] 3.32 0.02 2.47 -1.49 1.67 3.28 4.93 8.19 10000 1
beta[Noz,Co] -0.58 0.02 2.26 -5.07 -2.11 -0.55 0.95 3.79 10000 1
beta[Noz,Ne] 1.02 0.02 2.12 -3.15 -0.41 0.98 2.42 5.31 10000 1
beta[Noz,Op] 2.04 0.02 2.30 -2.46 0.50 2.05 3.53 6.66 10000 1
beta[Noz,sex] 0.29 0.01 0.94 -1.54 -0.36 0.30 0.93 2.15 10000 1
beta[Eli,B ] 0.17 0.02 2.28 -4.40 -1.35 0.21 1.71 4.56 8342 1
beta[Eli,Ex] -0.22 0.02 2.31 -4.73 -1.77 -0.22 1.32 4.35 10000 1
beta[Eli,Ag] -4.04 0.03 2.88 -9.81 -5.93 -3.98 -2.10 1.41 10000 1
beta[Eli,Co] 0.79 0.02 2.25 -3.62 -0.73 0.79 2.31 5.12 10000 1
beta[Eli,Ne] 0.70 0.02 2.07 -3.31 -0.69 0.66 2.09 4.87 10000 1
beta[Eli,Op] 0.84 0.02 2.27 -3.57 -0.70 0.83 2.36 5.26 10000 1
beta[Eli,sex] -0.65 0.01 0.99 -2.69 -1.29 -0.63 0.01 1.24 10000 1
beta[Hon,B ] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
beta[Hon,Ex] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
beta[Hon,Ag] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
beta[Hon,Co] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
beta[Hon,Ne] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
beta[Hon,Op] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
beta[Hon,sex] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10000 NaN
こんなにたくさんある事後分布の中で意味のある係数 (95%確信区間に正負両方の値を含まないもの) はなんと、beta[Kot,sex]のことりちゃんのみであるようです。ちなみに負の値でした。
つまり、「(穂乃果ちゃんと比べて)ことりちゃんは女の子に愛されやすい」 という結果が観察されました。
そして
「にこちゃんを好きな人は経験に開放的おじさんである」
という仮説はびっくりするくらい支持されませんでした。
結果のおまけ. 階層モデル
これも結果が出てないので今後変量要因とかぶちこんでみたいRstanユーザーさんに向けて一応載せておきます。
このコードは年齢を無駄に変量要因に組み込んでいるものです。結果は割愛します。
data {
int<lower=1> N; // サンプルサイズ
int<lower=1> P; // 説明変数の数
int<lower=1> K; // カテゴリー数
int<lower=0> n_age; //max年齢
int<lower=1, upper=K> y[N];
vector[P] x[N];
int<lower=0,upper=n_age> age[N];
}
parameters {
matrix[K-1, P] beta_raw;
vector[n_age] a; //変量要因(切片)
real<lower=0,upper=100> sigma_a; //変量要因の分散
}
transformed parameters {
matrix[K, P] beta; // K-1 handling
// beta K-1 handling
for (k in 1:(K-1))
beta[k] = beta_raw[k];
beta = append_row(beta_raw, rep_row_vector(0, P)); //がんばるやつ
}
model {
for (k in 1:(K-1))
beta_raw[k] ~ normal(0, 5);
for (i in 1:N)
y[i] ~ categorical(softmax(beta * x[i]+a[age[i]]));
a ~ normal(0,sigma_a);
}
考察
本稿において、誰を推すかというキャラクターの選択に外向性や神経症傾向などのパーソナリティ特性がどのようにかかわっているのか。
というリサーチクエスチョンに対して
ことりちゃんだけは辛うじて女の子から愛されやすいようだ。
という結論が得られた。性別はパーソナリティじゃねえ。
この結果が得られた要因として、
$μ's$ のメンバーはどんな人間にも愛される。
という結論も考えることができる。
しかし、本研究の限界としてサンプルサイズが多くないこと。そしてさらに重要な要因として、回答者の μ's メンバーに対する事前知識に関する項目をとっていなかったことが挙げられる。当然、彼女たちのことを詳しく知る人物とそうでない人物では、ポスターに対するキャラクター選択は異なるプロセスが想定される。
そうした新たな要因・項目を含めたうえで再度検討すれば、キャラクターの選好と個人特性の関連を示すことができるかもしれない。
以上、Stanを使ったデータ分析の一例でした。