レポート[深層学習 day2]

Section1 : 勾配消失問題

要点

シグモイド関数の入力値が0から離れているとき，その勾配は小さくなり，逆伝播での勾配の値がどんどん小さくなって最後は消えてしまう．これを勾配消失問題と呼ぶ．この問題を解消するために，以下の3つの方法を説明する．

• 活性化関数の選択
  ReLU関数は$x>0$では勾配は$1$で一定であるため，勾配消失することはない．

• 重みの初期値設定
  Xavierによれば，重みの要素を，前の層のノード数の平方根で除した値とすればよい．

• バッチ正規化
  ミニバッチ単位で，入力値のデータの偏りを抑制する．

実装演習

勾配消失問題の解消を狙いとして，いくつかの活性化関数と重みの初期値設定の組み合わせで精度検証する．
精度検証を行う条件は以下である．

	活性化関数	重みの初期値設定
case1	sigmoid	gauss
case2	ReLU	gauss
case3	sigmoid	Xavier
case4	ReLU	He
case5	sigmoid	He
case6	ReLU	Xavier

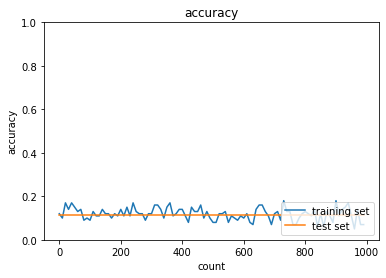
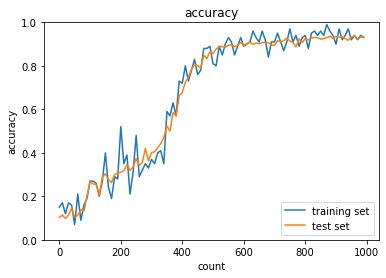
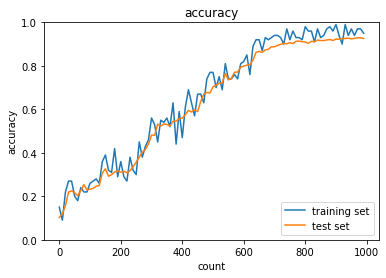
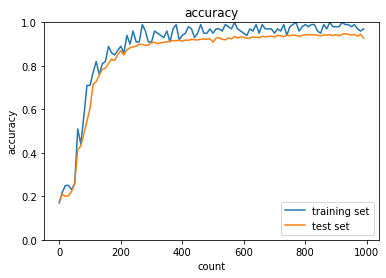
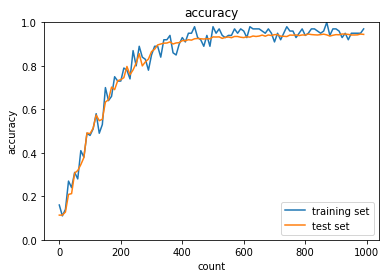
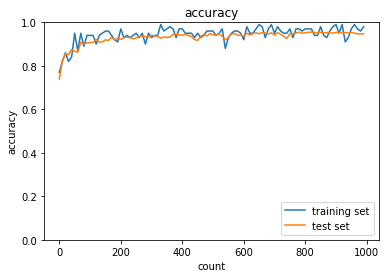
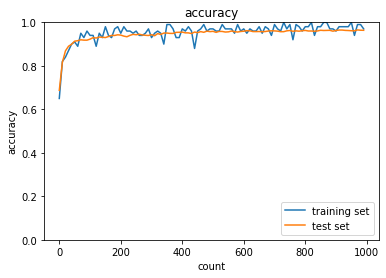
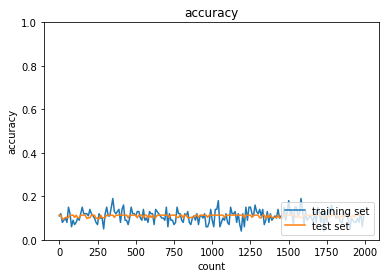
case1について，活性化関数がシグモイド関数では勾配消失問題によって，学習量が増えても精度向上していない．case2のように，ReLU関数を使用すると，精度向上できている．また，case3~6のように重みの初期値設定をXavier，Heにすることで学習の初期段階から精度が向上することが分かる．

case1

case2

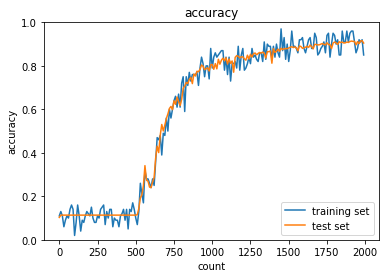
case3

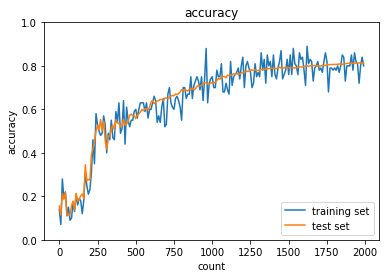
case4

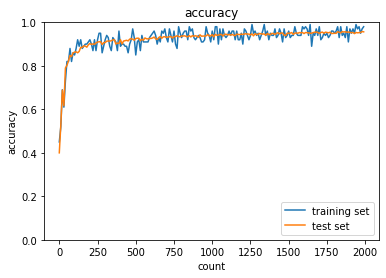
case5

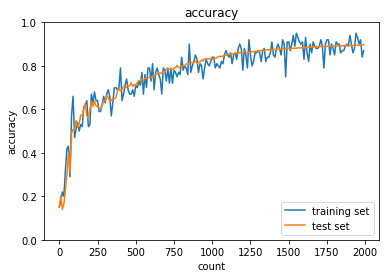
case6

「確認テスト」について自身の考察結果

連鎖律を用いて以下の式における$dz/dx$を求める．
$$z=t^2,t=x+y$$
$$\frac{dz}{dx}=\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}=2t\cdot 1=2(x+y)$$
シグモイド関数の微分は以下のようになる．
$$f(x)=\frac{1}{1+\exp {(-x)}}$$
$$f'(x)=f(x)(1-f(x))$$
シグモイド関数を微分したとき，入力値が0の時に最大値をとる．その値を求める．
まず，$f(0)=0.5$である．それを用いると，次式からシグモイド関数の微分の最大値は$0.25$となる．
$$f'(0)=0.5\cdot(1-0.5)=0.25$$
重みの初期値を0に設定すると重みが均一になってしまうため，重みが多数あることの意味がなくなってしまう．
バッチ正規化の利点は以下の通りである．

• 学習を早く信仰させることができる．
• 初期値にそれほど依存しない．
• 過学習を抑制する．

Section2 : 学習率最適化手法

要点

パラメータ最適化のために，学習率は初期段階では大きく設定，徐々に小さくすべきである．このように，学習率を段階に応じて可変にすることで高効率高精度のパラメータ探査を行う．パラメータ手法として，以下の4つを説明する．

• モメンタム
  誤差をパラメータで微分したものと学習率の積を減算した後，現在の重みに前回の重みを減算した値と慣性の積を加算する方法である．数式を下に示す．
  $$V_t=\mu V_{t-1}-\epsilon \nabla E$$
  $$w^{(t+1)}=w^{(t)}+V_t$$
  モメンタムのメリットは大域的最適解となること，パラメータが谷に入ってから最適値に行きつくまでの時間が早いことである．

• AdaGrad
  誤差をパラメータで微分したものと再定義した学習率の積を減算する方法である．学習率が徐々に小さくなるため鞍点問題を引き起こすことがある．

• RMSProp
  誤差をパラメータで微分したものと再定義した学習率の積を減算する方法である．こちらは，ハイパーパラメータの調整が必要な場合が少ないという利点がある．

実装演習

各最適化手法を用いて精度検証を行った．SGDに対して，各改善型モデル，Momentum，AdaGrad，RMSPropは精度が高いことが分かる．また，高度な最適化手法と適切な活性化関数，重みの初期値設定を組み合わせることでより高効率高精度なモデルができる．実際にAdamについて，sigmoid，gaussをReLU, Xavierに変更すると，より高効率高精度な学習ができた．さらにバッチ正規化を行うことで，ますます高効率高精度になる．

SGD

Momentum

AdaGrad

RMSProp

Adam，sigmoid，gauss

Adam, ReLU, Xavier

Adam, ReLU, Xavier，バッチ正規化

「確認テスト」について自身の考察結果

※モメンタム・AdaGrad・RMSPropの特徴は「要点」に含めて記述した．

Section3 : 過学習

要点

過学習とは，パラメータを訓練データに適合させ過ぎることで，訓練誤差とテスト誤差との乖離が大きくなることである．その原因は層数，ノード数などのネットワークの自由度が大きいことである．対策として，正則化手法を利用することで過学習を抑制する．つまり，ネットワークの自由度に制約を設ける．
過学習の対策として，誤差に正則化項を加えることで重みを抑制する．ここで，Weight decay（荷重減衰）という手法を説明する．誤差関数$E_n(\boldsymbol w)$に正則化項を加算すると次式のようになる．

$$E_n(\boldsymbol w)+\frac{1}{p}\lambda ||x||_p$$

$$||x||_p=(|x_1|^p+\cdots +|x_n|^p)^{\frac{1}{p}}$$

過学習の対策としてもう一つ，ドロップアウトという手法を説明する．これは，ニューロンをランダムに消去しながら学習する手法である．

実装演習

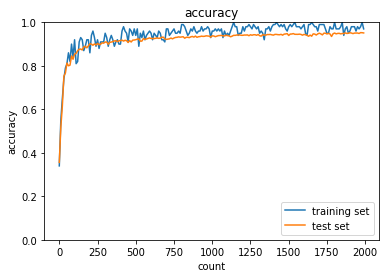
下図は学習データとテストデータの認識精度であり，過学習が起こっている．

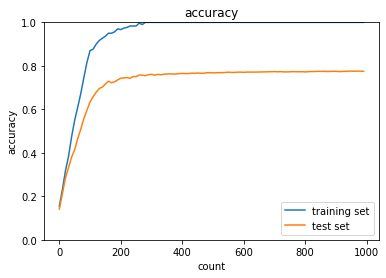
これに対して，L2ノルムによるWeight decayを適用すると，以下のようになり，先ほどと比べると過学習は抑制された．

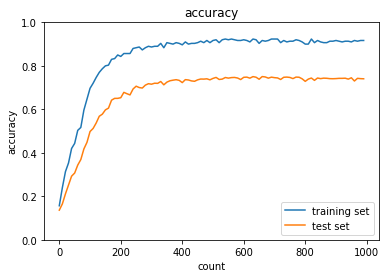
L1ノルムによるWeight decayを適用すると，以下のようになり，こちらも過学習は抑制された．しかし，学習に対する精度向上が不安定である．

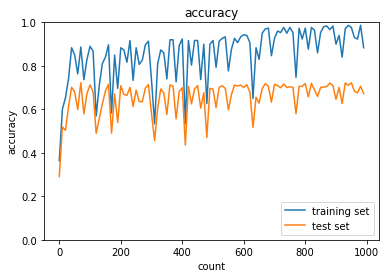
L1ノルムで正則化強度を$\lambda=0.005$から$\lambda=0.01$と大きくすると，予想どおり，過学習がより抑制されることを確認した．

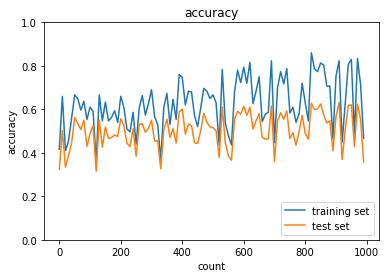
続いて，ドロップアウトを適用するとこちらも過学習が抑制されていることを確認できた．

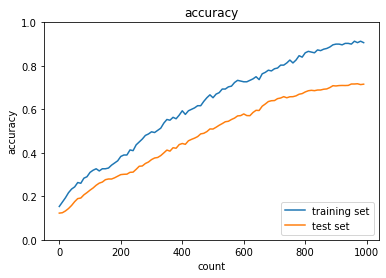
最後に，ドロップアウトとL1ノルムによるWeight decayを組み合わせたところ，先ほどよりは過学習が起こっていることが分かる．したがって，認識精度向上と過学習の抑制を両立させるための最適な手法の選定をモデルの特性から仮説ベースで行うことが必要である．

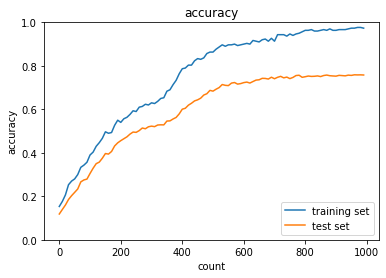
「確認テスト」について自身の考察結果

線形モデルの正則化手法の一つであるRidge回帰の特徴として，ハイパーパラメータを大きな値に設定すると，すべての重みが限りなく0に近づく．
L1正則化はL2正則化に比べて精度は低下するが，スパース化により計算リソースを省力化できる．

Section4 : 畳み込みニューラルネットワークの概念

要点

畳み込みニューラルネットワーク（convolutional neural network : CNN）は，画像認識や音声認識などに使用されるニューラルネットワークである．CNNは畳み込み層とプーリング層という新な層を使用する．畳み込み層は，例えば画像の場合，縦・横・チャンネルの3次元のデータを学習できる．
CNNを取り扱うためにいくつかの用語を説明する．

パディング

CNNの処理を行う際，パディングという処理を行う．これは，任意のサイズの出力データを得るために入力データの周囲に固定のデータを埋めることである．

ストライド

ストライドはフィルタを適用する窓の間隔である．例えばストライドを2に設定すると，各要素の出力計算でフィルターの間隔を2つずつ移動させる．

チャンネル

チャンネルはデータの3次元目の次元に相当する概念である．全結合では3次元データは1次元データとして処理していた．そのため，各チャンネル間の関連性が学習に反映されなかった．チャンネルはこの課題解決の一つの対策となる．

プーリング層

プーリングは，縦・横方向の空間を小さくする演算である．Maxプーリングはある領域をひとつの要素に集約する際，最大値を適用する．Averageプーリングは領域の値を平均してひとつの要素とする．

実装演習

im2colは他次元配列のデータを2次元データに変換するメソッドである．2次元データに置き換えることで，多くのライブラリを活用できるというメリットがある．下の出力結果のように3次元データの各窓を列データに置き換えることで2次元データを出力できた．

========== input_data ===========
 [[[[35. 83.  1.  3.]
   [68. 96. 70. 91.]
   [45. 80. 68. 97.]
   [37. 82. 18. 88.]]]


 [[[31. 67. 44.  3.]
   [56. 43.  7. 10.]
   [76. 28. 82.  6.]
   [20. 38. 68.  1.]]]]
==============================
============= col ==============
 [[35. 83.  1. 68. 96. 70. 45. 80. 68.]
 [83.  1.  3. 96. 70. 91. 80. 68. 97.]
 [68. 96. 70. 45. 80. 68. 37. 82. 18.]
 [96. 70. 91. 80. 68. 97. 82. 18. 88.]
 [31. 67. 44. 56. 43.  7. 76. 28. 82.]
 [67. 44.  3. 43.  7. 10. 28. 82.  6.]
 [56. 43.  7. 76. 28. 82. 20. 38. 68.]
 [43.  7. 10. 28. 82.  6. 38. 68.  1.]]
==============================

「確認テスト」について自身の考察結果

サイズ6x6の入力画像をサイズ2x2のフィルタで畳み込みを行ったときの出力画像のサイズを求める．条件として，ストライドとパディングは1である．次式から出力サイズ$(OH,OW)$を計算する．
$$OH=\frac{H+2P-FH}{S}+1$$
$$OW=\frac{W+2P-FW}{S}+1$$
$$OH=OW=\frac{6+2\cdot 1-2}{1}+1=7$$
したがって出力サイズは7x7である．

Section5 : 最新のCNN

要点

ここでは，最新のCNNの概要を説明する．ここでは，代表的なAlexNetおよびCNNの元祖であるLeNetを説明する．

LeNet

畳み込み層とプーリング層を連続で行い，最後に全結合層を経て結果を出力する．史上初のCNN構造である．

AlexNet

5層の畳み込み層およびプーリング層など，それに続く3層の全結合層から構成させるモデル構造である．LeNetとの相違点は以下である．

• 活性化関数にReLUを用いる．
• LRNという局所的正規化を行う層を用いる．
• ドロップアウトを使用する．

実装演習

なし

「確認テスト」について自身の考察結果

なし

参考文献

斎藤 康毅 (2016) : ゼロから作るDeep Learning ―Pythonで生部ディープラーニングの理論と実装 オライリージャパン