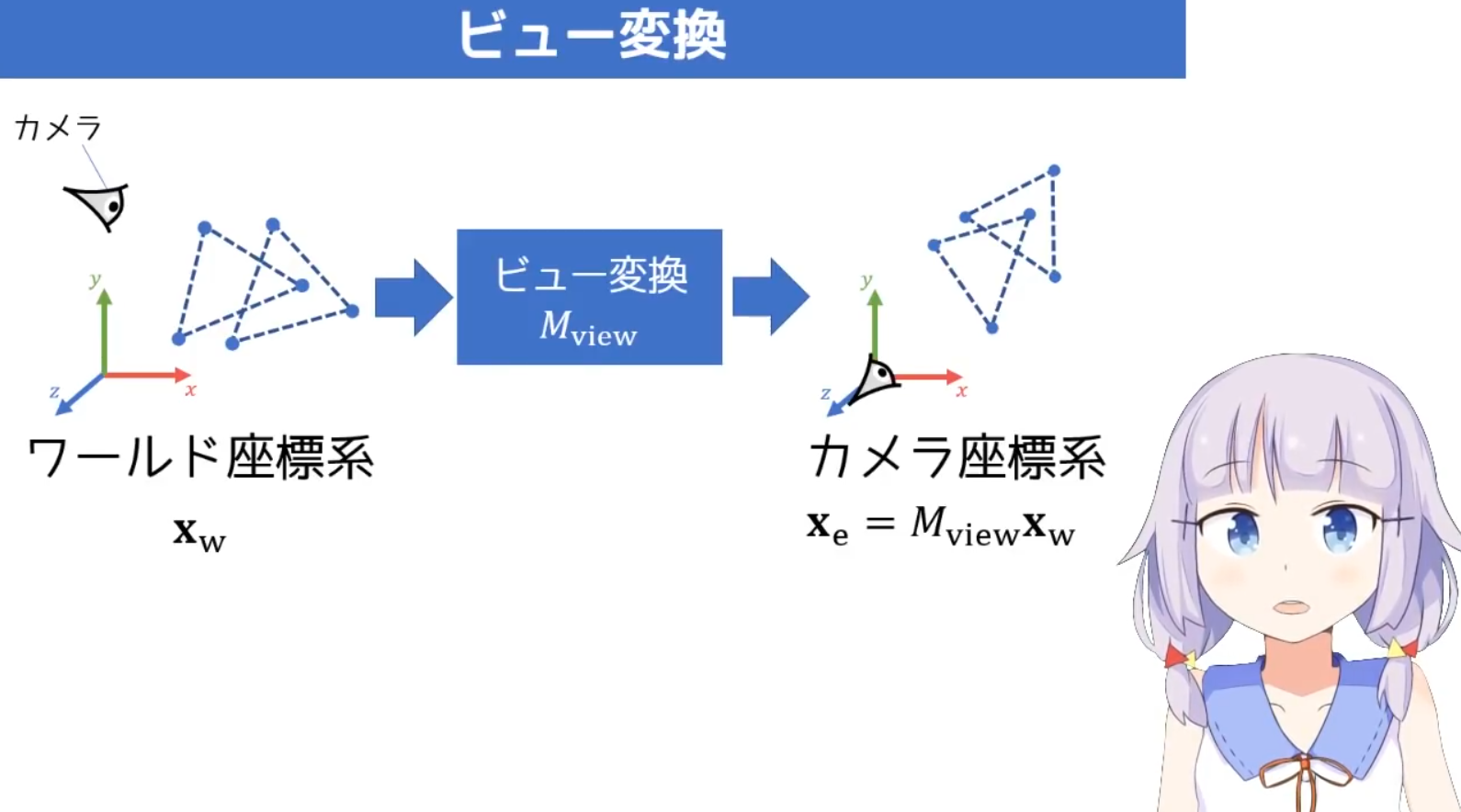
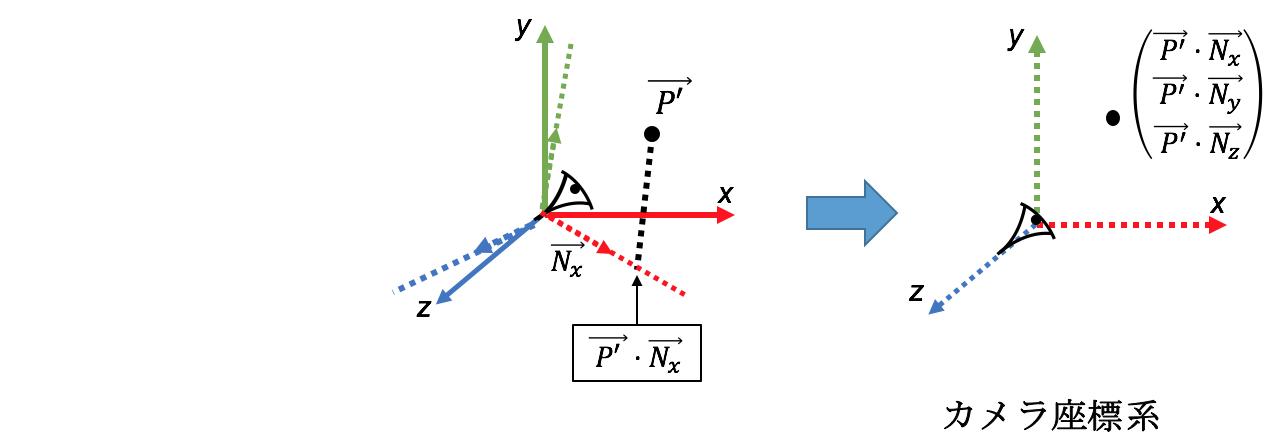
今回は三葉レイさんの動画を参照して、自身でC++11によるソフトウェアラスタライザ実装を行いました。
動画内では省略されていた変換行列の導出過程をメインに書いています。
行列計算にはEigenライブラリを使用しています。
ソースコードはGithubでまとめて公開しています。
全体像
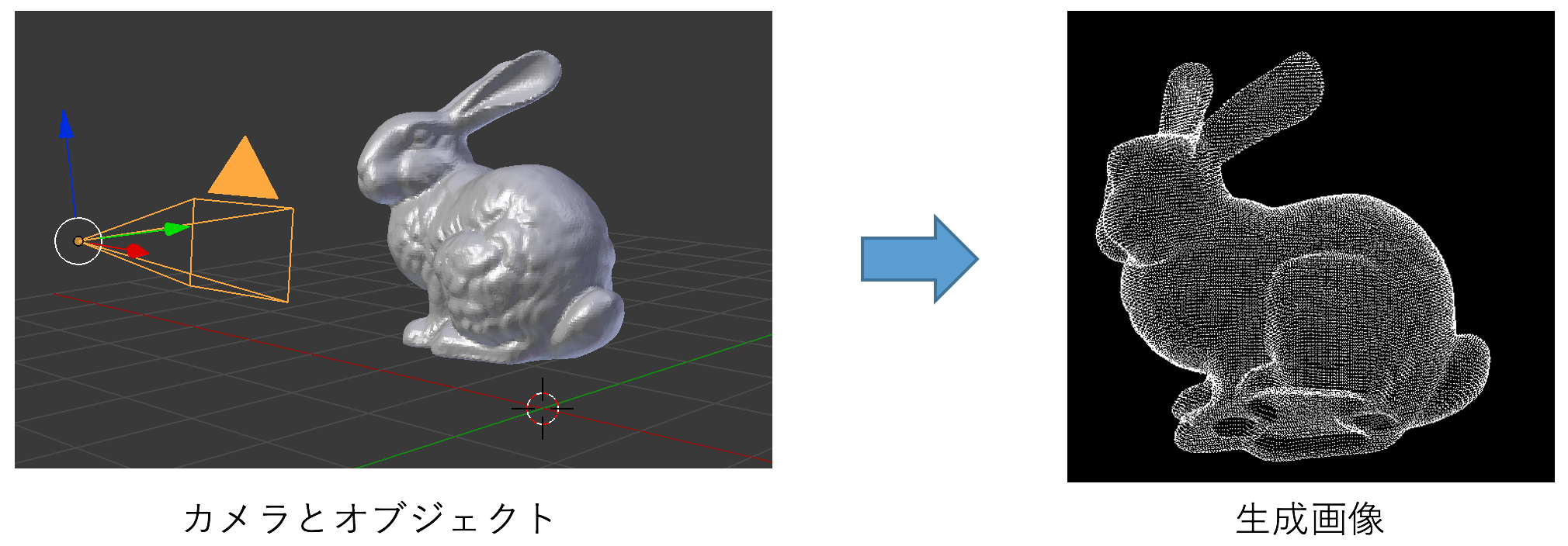描画シーンはカメラ設定とオブジェクトにより定義される。オブジェクトは.objファイルから読み込むことにし、今回は`OBJ_Loader.h`の[ライブラリ](https://github.com/Bly7/OBJ-Loader)を使用している。三角形の頂点情報を記録するための`triangle`クラスを用意し、オブジェクトを構成する三角メッシュ1つをtriangleベクトル`vector T`の1要素として記録する。カメラ視点は`camera.h`内で設定しており、詳しくは次のセクションで述べる。今回は、`T`に記録された三角形の頂点を適切に座標変換して、カメラから見える頂点をプロットした2次元画像を生成することが目的となる。
#include <Eigen/Dense>
#include "camera.h"
#include "triangle.h"
#include "OBJ_Loader.h"
// objファイルを読み込む関数
void Loading_obj (vector<Triangle>& T, objl::Loader Loader, string Filename) {
Loader.LoadFile(Filename);
for (int i = 0; i < Loader.LoadedMeshes.size(); i++) {
objl::Mesh curMesh = Loader.LoadedMeshes[i];
for (int j=0;j<curMesh.Indices.size();j+=3) {
int i_A = curMesh.Indices[j];
int i_B = curMesh.Indices[j+1];
int i_C = curMesh.Indices[j+2];
Vector4d A; A << curMesh.Vertices[i_A].Position.X, curMesh.Vertices[i_A].Position.Y, curMesh.Vertices[i_A].Position.Z, 1.0;
Vector4d B; B << curMesh.Vertices[i_B].Position.X, curMesh.Vertices[i_B].Position.Y, curMesh.Vertices[i_B].Position.Z, 1.0;
Vector4d C; C << curMesh.Vertices[i_C].Position.X, curMesh.Vertices[i_C].Position.Y, curMesh.Vertices[i_C].Position.Z, 1.0;
Triangle T_temp(A, B, C);
T.push_back(T_temp);
}
}
}
int main() {
int nx = 512;
int ny = 512;
// モデル読み込み https://github.com/Bly7/OBJ-Loader
vector<Triangle> T{};
objl::Loader Loader;
Loading_obj(T, Loader, "bunny.obj");
// カメラインスタンス生成
Camera cam; // 視点、画面位置を指定
// ワールド座標変換
// ~
// ビュー変換
// ~
// 投影変換
// ~
// -> デバイス座標系
// ~
// ビューポート変換
// ~
// ファイル出力 (https://programming.pc-note.net/cpp/filestream.html)
ofstream ofs("image.ppm");
ofs << "P3\n" << nx << " " << ny << "\n255\n";
for (int j=ny-1;j>=0;j--) {
for (int i=0;i<nx;i++) {
float temp_value = 0.0; // 0.0で黒、1.0で白を描画
float r = temp_value;
float g = temp_value;
float b = temp_value;
int ir = int(255.99*r); // 0~255の整数値(8bit)でppmに書き込み
int ig = int(255.99*g);
int ib = int(255.99*b);
ofs << ir << " " << ig << " " << ib << endl;
}
}
return 0;
}
#ifndef TRIANGLE_H
#define TRIANGLE_H
using Eigen::Vector4d;
class Triangle {
public:
Vector4d A;
Vector4d B;
Vector4d C;
Triangle() {}
Triangle (const Vector4d& vertix_A, const Vector4d& vertix_B, const Vector4d& vertix_C) {
A = vertix_A;
B = vertix_B;
C = vertix_C;
}
void Init (const Vector4d& vertix_A, const Vector4d& vertix_B, const Vector4d& vertix_C) {
A = vertix_A;
B = vertix_B;
C = vertix_C;
}
};
#endif
カメラの設定
まずはカメラ視点の設定を行う。必要となるのは、カメラの位置座標(origin)、注視点座標(endpoint)、視点の上方向を表す単位ベクトル(up_vec)である。この情報を元にしてカメラ座標系のx,y,zベクトル(x_vec,y_vec,z_vec)を計算することができる。z_vecはカメラの後方を向く単位ベクトルであると定義すると、以下の図のようにz_vec,x_vec,y_vecを順に計算することができる。
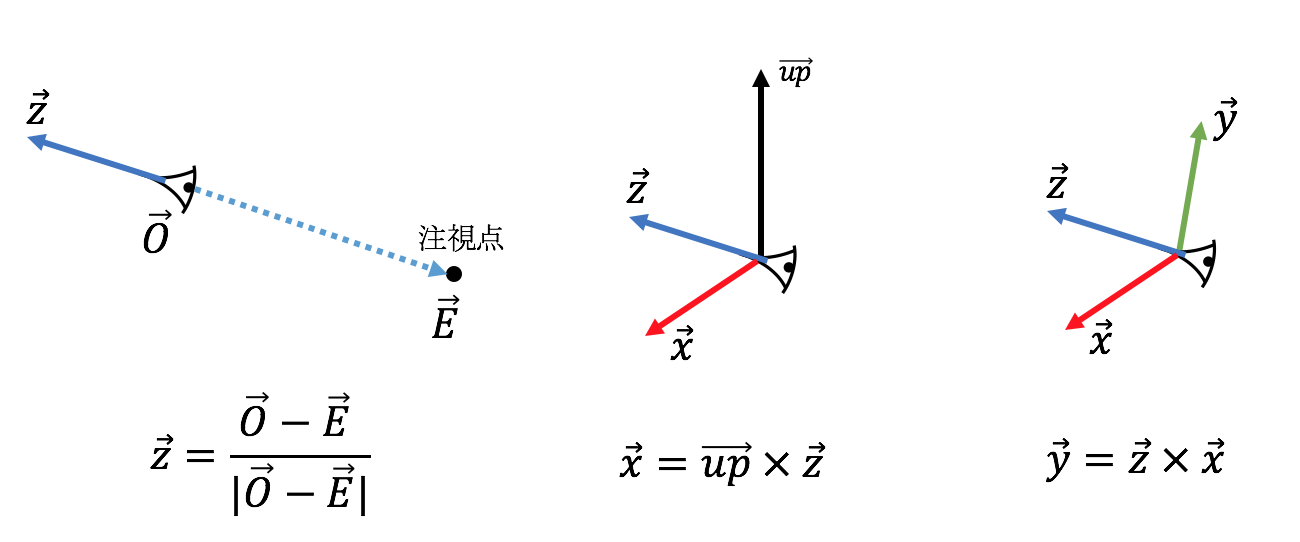
次に、仮想スクリーンの設定を行います。以下のように、距離$n\sim f$の範囲のオブジェクトを描画して、縦横($w,h$)のスクリーンに投影するとする。
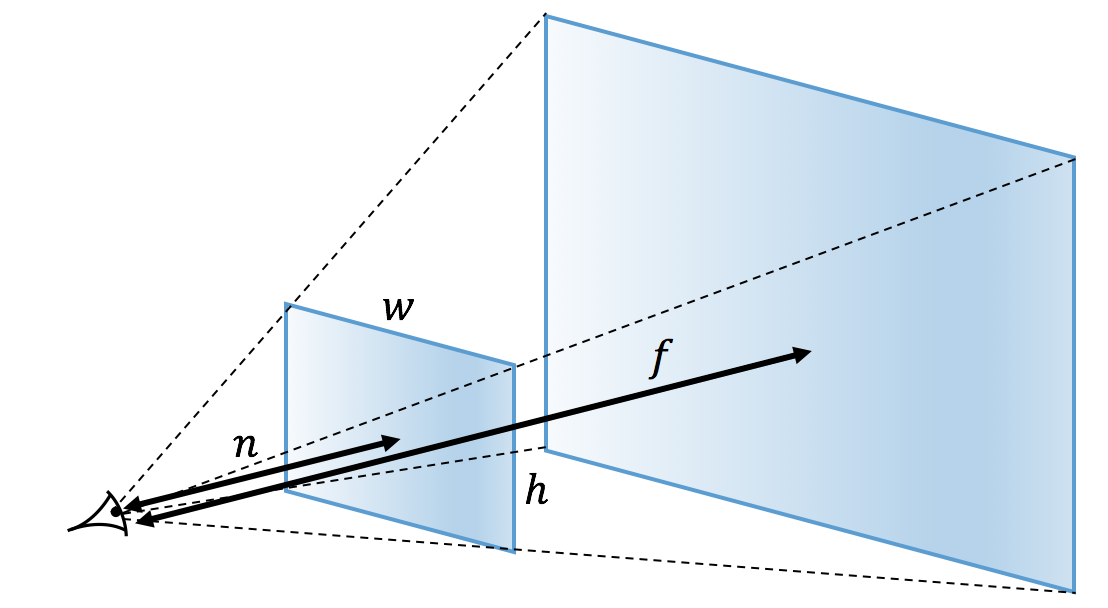
これらの情報をcamera.h内で定義する。
class Camera {
public:
Vector3d origin, endpoint, up_vec;
Vector3d x_vec, y_vec, z_vec;
float n, f, w, h;
Camera() {
// sphere-cone.obj
origin << 0.0,6.0,28.0;
endpoint << -0.2,1.6,0.0;
up_vec << 0.0,1.0,0.0;
n = 2.0;
f = 10.0;
w = 1.0;
h = 1.0;
z_vec << (origin-endpoint)/(origin-endpoint).norm();
x_vec << up_vec.cross(z_vec);
y_vec << z_vec.cross(x_vec);
}
};
ビュー変換
ワールド座標系で定義されたカメラ位置$\vec C$、カメラ座標系を表す単位ベクトル$\vec{N_x},\vec{N_y},\vec{N_z}$を用いて、点Pの位置$\vec P$をカメラ座標系で表してみる。
- カメラ位置を原点とするような座標へ平行移動する変換行列は次のように書ける。
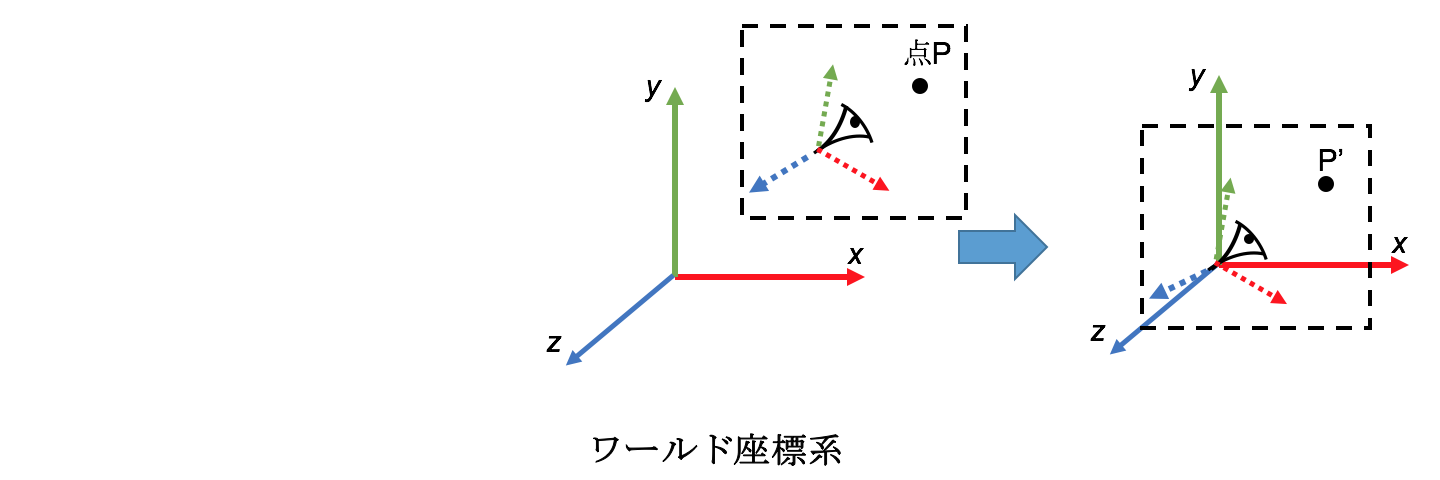
\begin{eqnarray}
\begin{pmatrix}
P_x \\ P_y \\ P_z \\ 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
P_x-C_x \\ P_y-C_y \\ P_z-C_z \\ 1
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 0 & -C_x \\
0 & 1 & 0 & -C_y \\
0 & 0 & 1 & -C_z \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
P_x \\ P_y \\ P_z \\ 1
\end{pmatrix}
\end{eqnarray}
2.$,$カメラ座標系に合わせる様な回転を行う。
\begin{eqnarray}
\begin{pmatrix}
\begin{pmatrix} \ \\ \vec{P'} \\ \ \end{pmatrix} \\ 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
\vec{P'} \cdot \vec{N_x} \\ \vec{P'} \cdot \vec{N_y} \\ \vec{P'} \cdot \vec{N_z} \\ 1
\end{pmatrix}
=
\begin{pmatrix}
( & \vec{N_x} & ) & 0 \\
( & \vec{N_y} & ) & 0 \\
( & \vec{N_z} & ) & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
\begin{pmatrix} \ \\ \vec{P'} \\ \ \end{pmatrix} \\ 1
\end{pmatrix}
\end{eqnarray}
これら2つの行列によるビュー変換は以下のように書ける。(動画内では順番を逆にしたような変換行列が示されていましたが、おそらく間違いだと思われます)
// ビュー変換
// 4次元同次座標系での変換行列
Matrix4d view_matrix, temp_matrix1, temp_matrix2;
temp_matrix1 << // カメラpositionに平行移動させる行列
1.0, 0.0, 0.0, -cam.origin(0),
0.0, 1.0, 0.0, -cam.origin(1),
0.0, 0.0, 1.0, -cam.origin(2),
0.0, 0.0, 0.0, 1.0;
temp_matrix2 << // カメラ座標系の軸に合わせる様に回転する行列
cam.x_vec(0), cam.x_vec(1), cam.x_vec(2), 0.0,
cam.y_vec(0), cam.y_vec(1), cam.y_vec(2), 0.0,
cam.z_vec(0), cam.z_vec(1), cam.z_vec(2), 0.0,
0.0, 0.0, 0.0, 1.0;
view_matrix = temp_matrix2*temp_matrix1; // 上2つを合わせた行列
// 三角形の頂点全てに変換行列を作用させる
for (int i=0;i<T.size();i++) {
T[i].Init(view_matrix*T[i].A, view_matrix*T[i].B, view_matrix*T[i].C);
}
投影変換
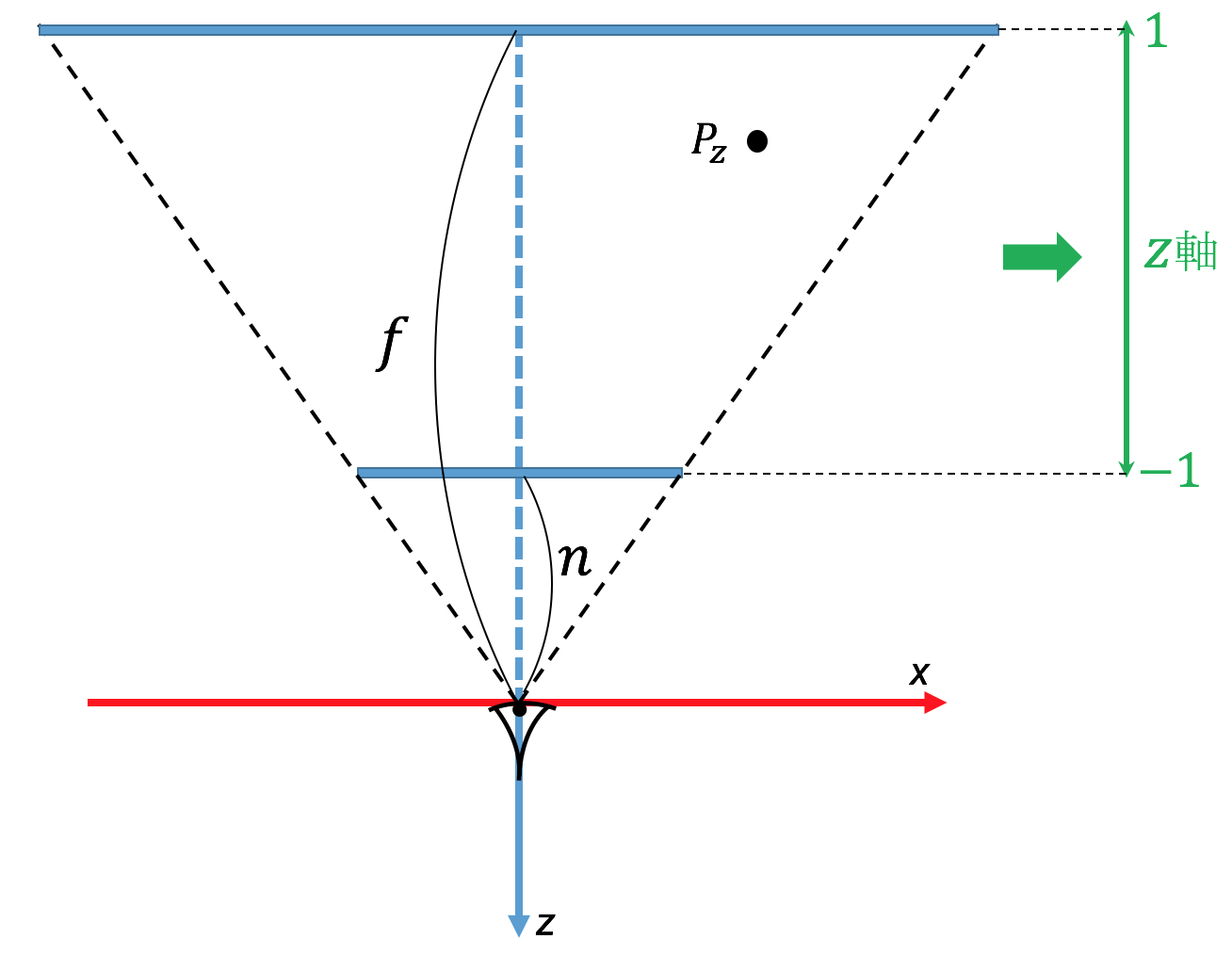
カメラ設定で仮想スクリーンと描画範囲を指定したことにより、描画する対象となる空間範囲は下左図のように正四角錐台の形を成している。投影変換では、各z軸に垂直な平面上でスケーリングすることにより、下右図のような$-1\sim1$の正規化座標を持つ立方体領域(デバイス座標系)に変換する。この変換により、カメラの仮想スクリーンに全ての三角形が投影されることになるので、2次元画像の生成には変換後の($x,y$)座標をそのまま用いればよくなる。また、投影変換によりカメラに近い三角形ほど拡大されることになる。
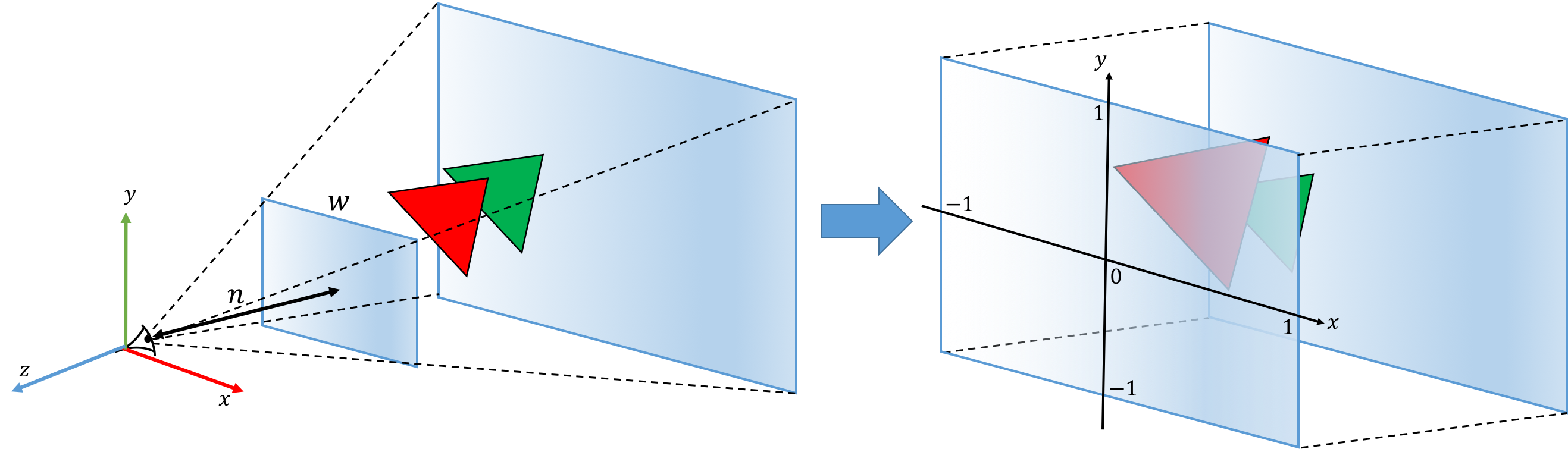
変換行列について、まず$x$座標について考えてみる。点Pを($P_x,P_y,P_z$)とすると、点Pを含みxy平面に垂直な平面内において点Pがどの位置にあるのかを計算することになる。
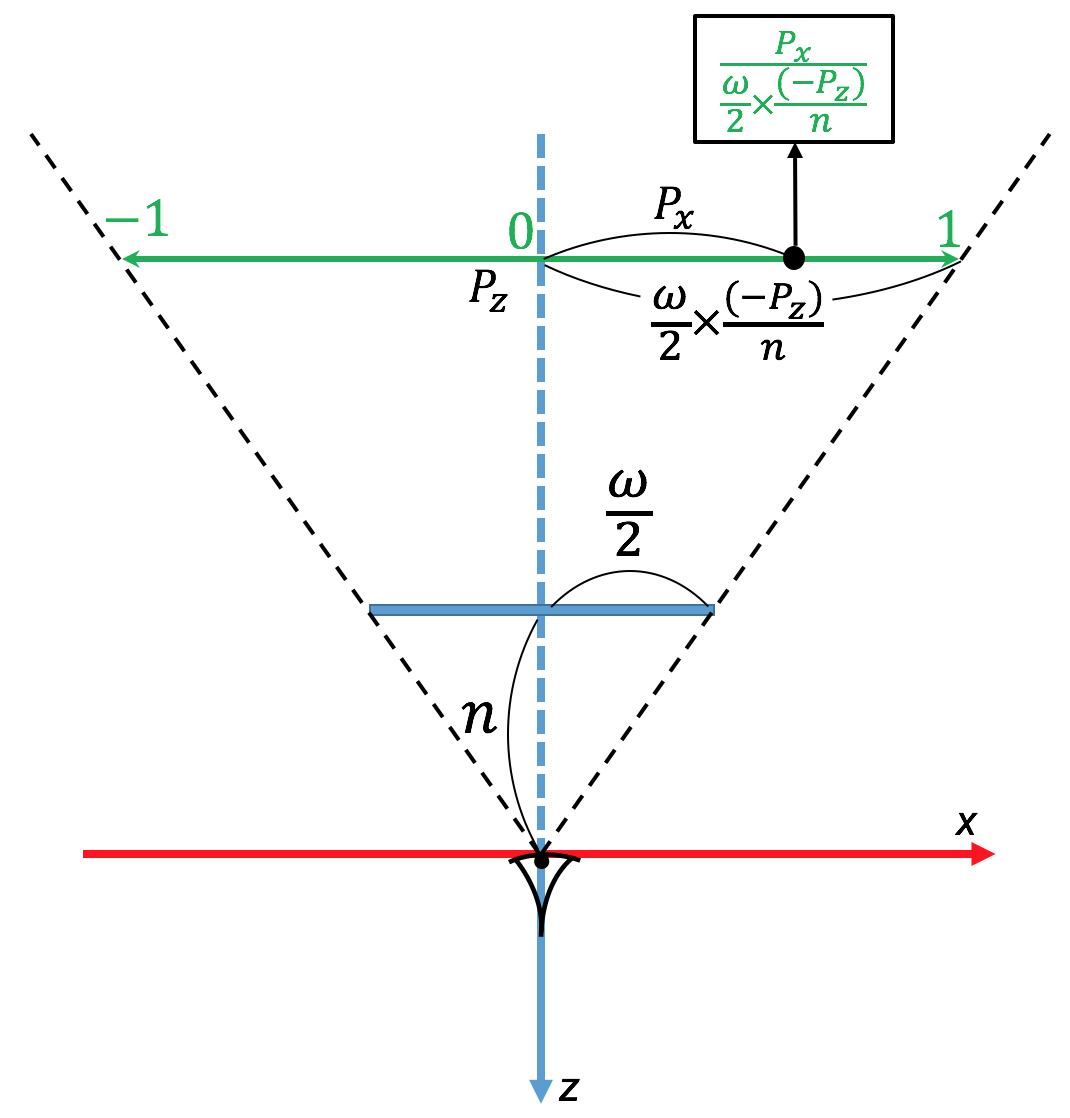
上図のように幾何学的に計算出来て、計算式は
\begin{eqnarray}
P_x \rightarrow P_x \cdot \frac{2n}{\omega} \frac{1}{(-P_z)}
\end{eqnarray}
となる。y座標についてもほぼ同じである。
z座標については、最も近い$z=-n$が-1に、遠い$z=-f$が1となるような変換を施す(下図)。この新たなz座標(デプス値)は、後のラスタライズの際に、視点から最も近い三角形を判別するために用いる。式的には、
\begin{eqnarray}
P_z \rightarrow \frac{f+n-\frac{2fn}{(-P_z)}}{f-n}
\end{eqnarray}
のように表される変換を用いる。
このように変換したデプス値は変換前後で線形の関係に無いことに注意。
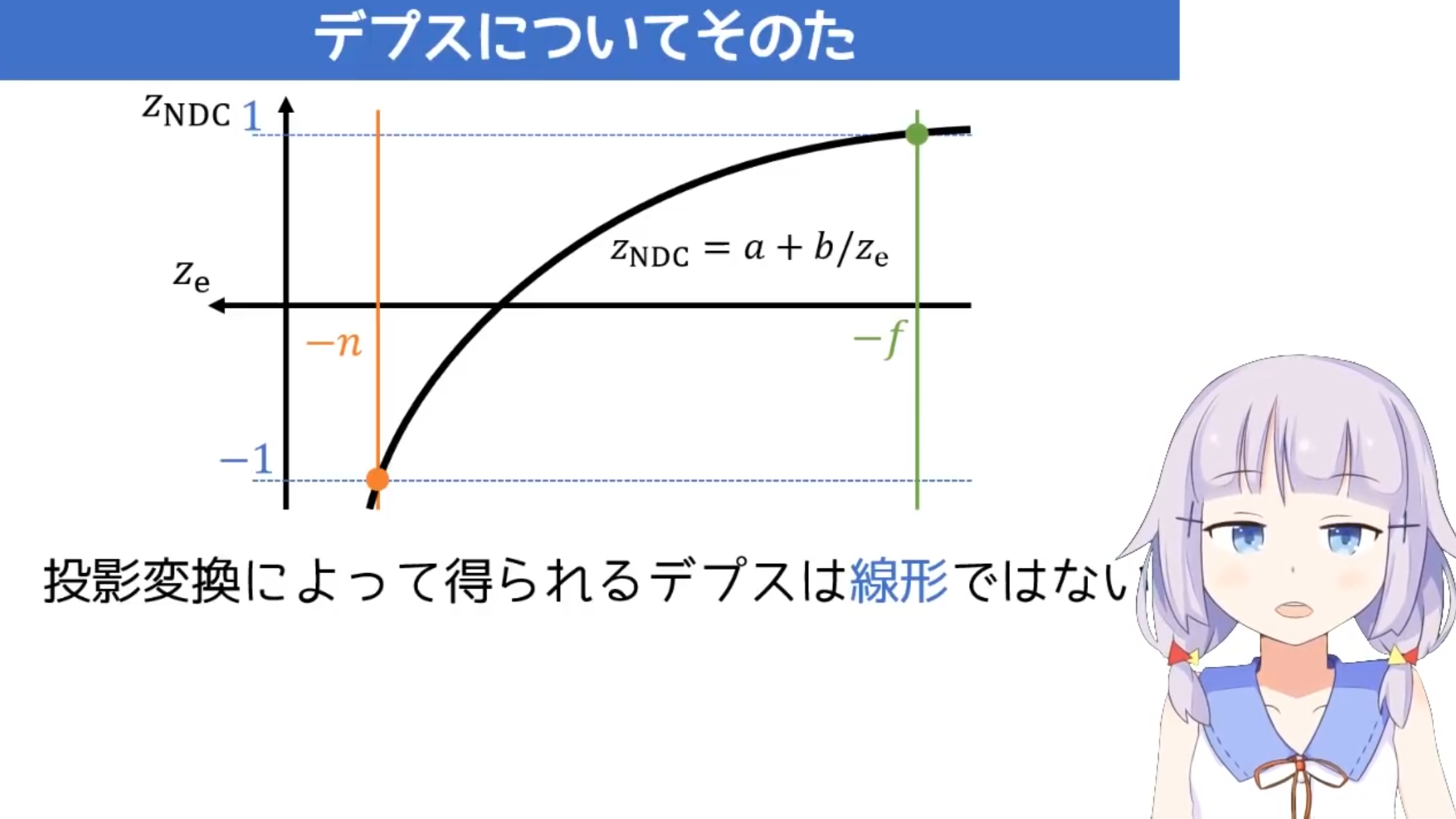
$P_z$で割るという操作は線形変換で実現出来ないので後で処理することにし、
\begin{eqnarray}
\begin{pmatrix}
P_x \\ P_y \\ P_z \\ 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
P_x \cdot \frac{2n}{\omega} \\ P_y \cdot \frac{2n}{h} \\ \frac{(f+n)(-P_z) - 2fn}{f-n} \\ -P_z
\end{pmatrix}
=
\begin{pmatrix}
\frac{2n}{\omega} & 0 & 0 & 0 \\
0 & \frac{2n}{h} & 0 & 0 \\
0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\
0 & 0 & -1 & 0
\end{pmatrix}
\begin{pmatrix}
P_x \\ P_y \\ P_z \\ 1
\end{pmatrix}
\end{eqnarray}
のような変換を施した後に、第4成分の$-P_z$で全体を割ることでデバイス座標系へと移ることが出来る。
// 投影変換
Matrix4d proj_matrix;
proj_matrix <<
2*cam.n/cam.w, 0.0, 0.0, 0.0,
0.0, 2*cam.n/cam.h, 0.0, 0.0,
0.0, 0.0, -(cam.f+cam.n)/(cam.f-cam.n), -2*cam.f*cam.n/(cam.f-cam.n),
0.0, 0.0, -1.0, 0.0;
for (int i=0;i<T.size();i++) {
T[i].Init(proj_matrix*T[i].A, proj_matrix*T[i].B, proj_matrix*T[i].C);
}
// -> デバイス座標系
for (int i=0;i<T.size();i++) {
T[i].A = T[i].A/T[i].A(3);
T[i].B = T[i].B/T[i].B(3);
T[i].C = T[i].C/T[i].C(3);
}
以上で主な頂点処理は終了である。後は三角形の頂点が位置するピクセルを割り出して画像出力する処理(ビューポート変換)を行うだけである。
GUIアニメーション化
OpenGL+GLFWのフレームワーク上で実装した。Worldビュー変換のところでオブジェクトを毎回少しずつ回転する操作を加えている。
これから
クリッピング処理 (その2)
三角形のラスタライゼーション (その3)
シャドウマッピング