ソフトウェアライスタライザ実装 その1 (頂点処理)の続きです。
クリッピングの処理について扱います。クリップ座標系の理解・クリッピングアルゴリズムについて詳しく書きます。
(今回も三葉レイさんの動画を参照・引用しています。)
クリッピング
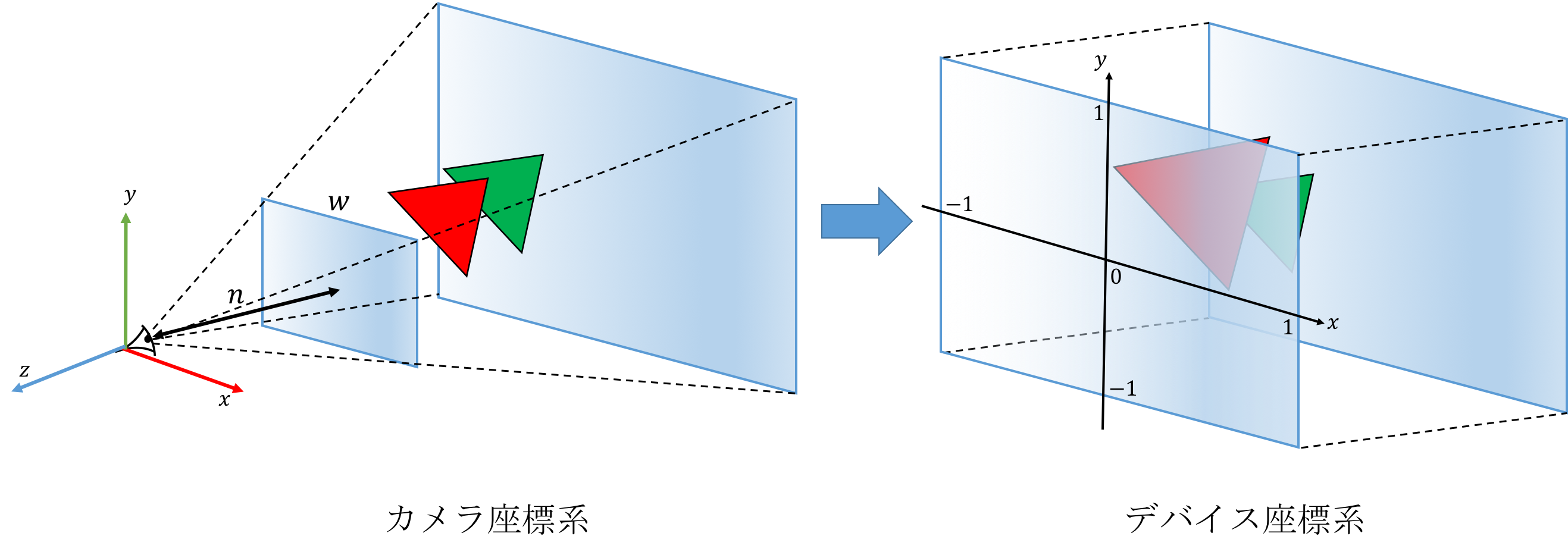
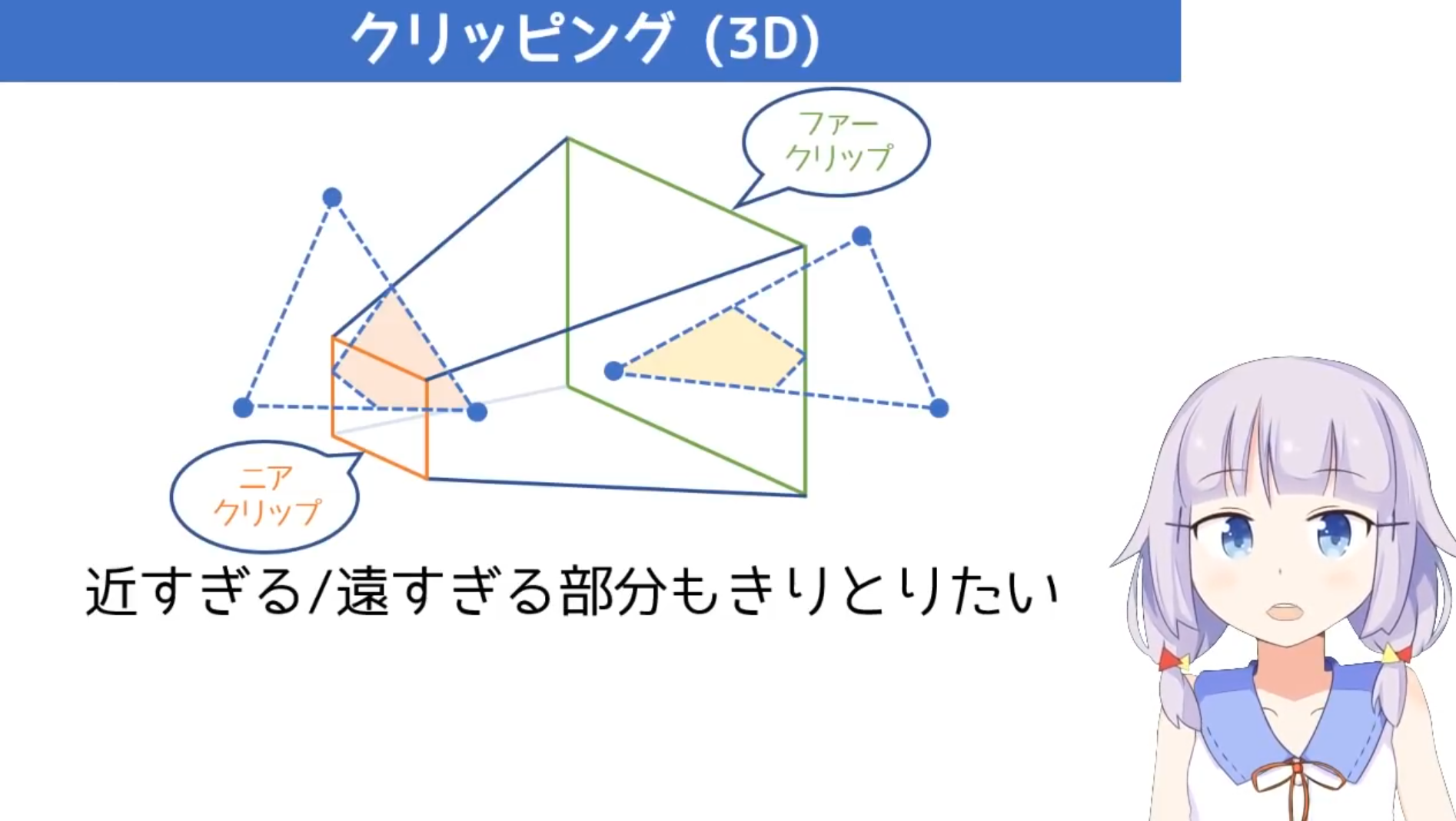頂点処理で行った投影変換では、下図のように描画対象である四角錐台領域を-1~1の座標に正規化した立方体領域に変換した。
この変換は、下式のように2ステップの計算で表されるのであった。
\begin{eqnarray}
\begin{pmatrix}
P_x \\ P_y \\ P_z \\ 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
P_x \cdot \frac{2n}{\omega} \\ P_y \cdot \frac{2n}{h} \\ \frac{(f+n)(-P_z) - 2fn}{f-n} \\ -P_z
\end{pmatrix}
\rightarrow
\begin{pmatrix}
P_x \cdot \frac{2n}{\omega(-P_z)} \\ P_y \cdot \frac{2n}{h(-P_z)} \\ \frac{(f+n) - \frac{2fn}{(-P_z)}}{f-n} \\ 1
\end{pmatrix}
\end{eqnarray}
クリッピングでは、描画したい領域内に存在しないオブジェクト情報を排除することを目的とする。
クリップ座標系
2段階の計算stepを経る投影変換において、中間状態をクリップ座標系と呼ぶ(後で見るようにこの座標系においてクリッピングを行うからである)。ここでは、投影変換の幾何学的な変化を図で追うことでクリップ座標系について理解しておく。
1段階目の線形変換では、
\begin{eqnarray}
\begin{pmatrix}
P_x \\ P_y \\ P_z \\ 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
P_x \cdot \frac{2n}{\omega} \\ P_y \cdot \frac{2n}{h} \\ \frac{(f+n)(-P_z) - 2fn}{f-n} \\ -P_z
\end{pmatrix}
\end{eqnarray}
のように、$x,y$座標については只の定数倍、$z$座標については複雑な式、$\omega$座標については$-z$の値が入ることになる。これを$x-z$平面(変換後は$x-\omega$平面)で切り取って見ると下図のようになっている。$\omega$軸は$z$軸を反転させただけなので縦方向には実質何の変化も起きていない。$x$軸方向には定数倍され、領域を区切る線分の傾きがちょうど1となるように調整されていることがわかる(これによりクリッピングの際に行う内外判定が簡単になる)。
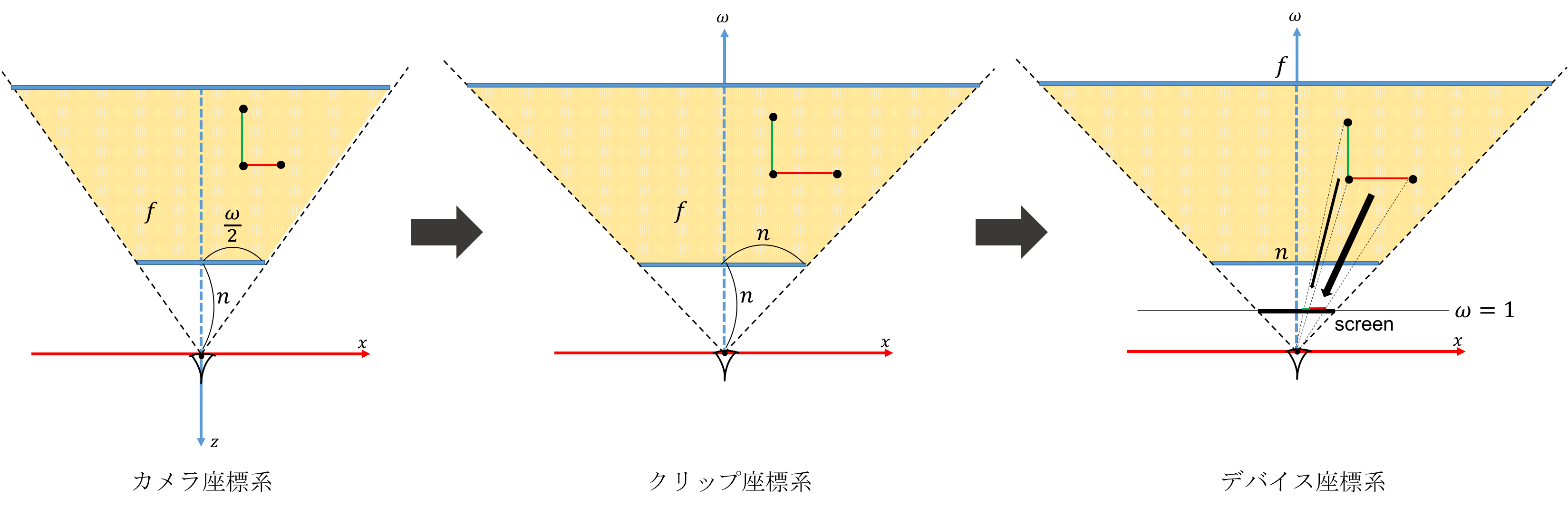
2段階目のデバイス座標系への変換では、$\omega$の値で$x$座標値を割るので、幾何学的には$\omega=1$に設置されたスクリーンに"投影"するような操作にあたる。
デバイス座標系でのクリッピング...
クリッピング処理をどの座標系で行うか考察してみる。デバイス座標系では描画対象領域が単純な立方体になっているため、領域の内外判定が最も容易いと思われる。しかし、問題点がいくつか存在するため、デバイス座標系でクリッピング処理を行うことは好ましくない。
(問題点1) カメラ後方にあるはずの頂点が領域内に投影されてしまう。
図のように$(x-\omega )$平面を縦に貫く実線矢印がある場合、どのように$\omega=1$のスクリーンに投影されるのかをみてみる。
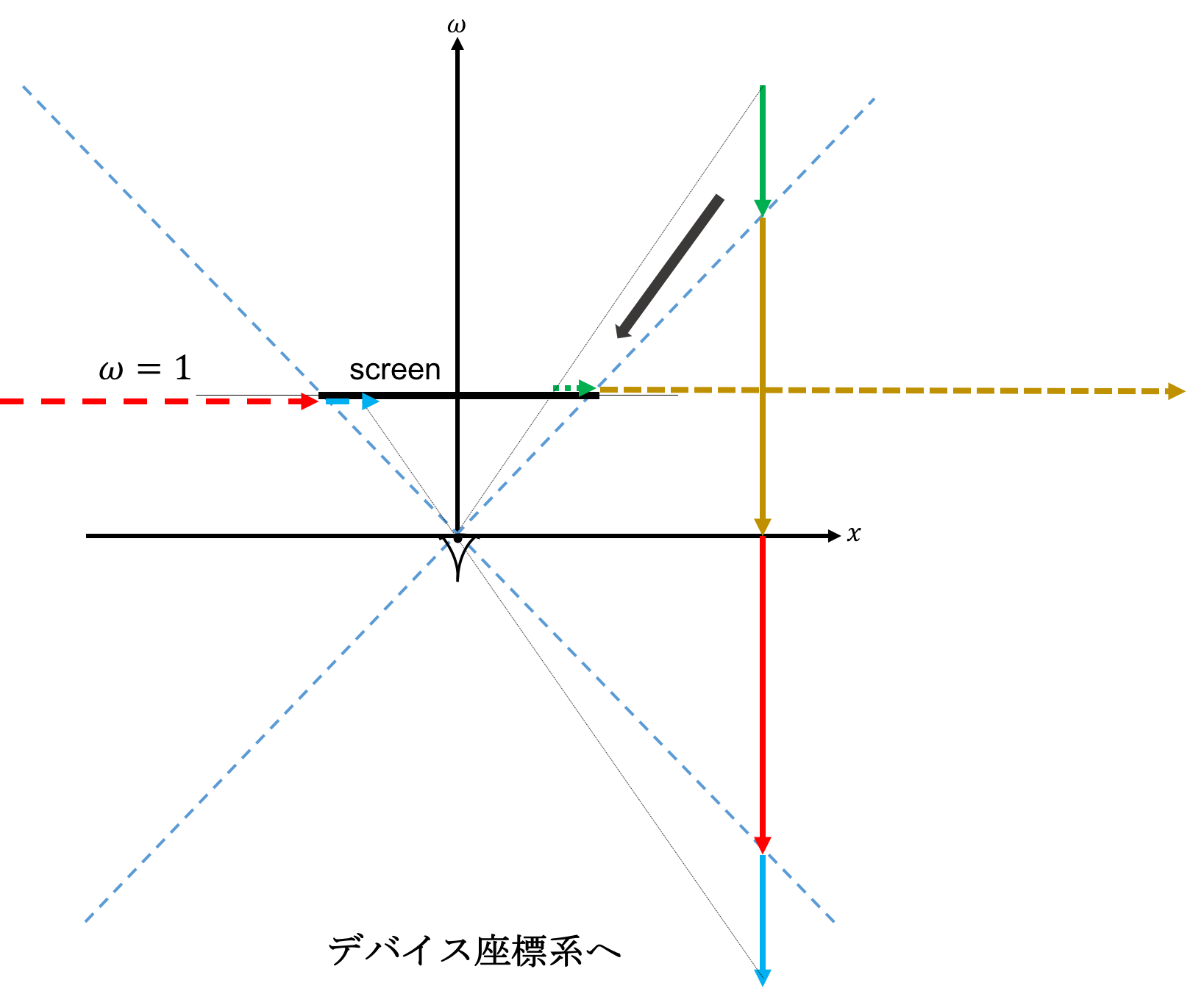
図では、実線矢印は同一色の点線矢印へと投影されている。このとき、カメラ後方(つまり$\omega<0$)にある線分も$\omega=1$のスクリーンに投影されてしまうことがわかる。
(解決策として、$\omega$値を保持しておいて、カメラ後方から投影されたものを除くような処理を行うことが考えられる。しかし、もし三角形の3頂点の一つが$\omega>0$側でもう一つは$\omega<0$側から来たものであるような場合、この2点を結ぶ線分は上図でみたように不連続に分断されることになるので、これをちゃんと追跡してクリッピング処理を行うことは困難となる。)
(問題点2) カメラに近い頂点は無限遠点に投影される
上図で見たように、カメラに近い座標点($\omega\simeq0$)はゼロ除算を行うことで発散することになり、数値計算上での扱いが面倒である。
クリップ座標系でのクリッピング
前セクションで見たように、デバイス座標系でクリッピングを行うことは難しい。また、カメラ座標系よりはクリップ座標系の方が領域の内外判定が容易いので、クリップ座標系でクリッピングを行う。(動画では、クリッピングによって三角形の数が増えるので、出来るだけ後で行う方が計算効率が良いという話であったが、完全に領域外の三角形は無視して減らすことが出来るという側面もあるため、一概には言えなそう。)
Sutherland-Hodgmanアルゴリズム (未完成)
はみ出た三角形をいい感じに区切る。。。