概要
AGC040(11/04 00:00 - 02:30) に参加したが問題Aしか解けなかったです。残り時間で問題B/Cも考えてみましたが、解法を思いつかず、時間切れ。で、復習で問題Bの解法をみてみたのですが、すぐに理解できない部分があったので考えてみました。結果としては理解できました（できたつもり）。Qiita、Overleafの練習も兼ねて備忘録的なメモを残します。
対象にした問題と解法で即時で咀嚼できなかったこと
対象にした問題はAtCoderのAGC040, B-Two Contests。解説はこちらAtCoderのAGC040 解説PDFにあります。
そのなかで即時で咀嚼できなかったのことの一つは以下の部分
これをみて「『という形です』と言い切っているけど。うーん？それってそう言い切れるの？なんで？タイブレーク？」となるアルゴリズム弱々の私。
問題の単純化と言い換え
いろいろゴチャゴチャしてて考えにくいので問題を次のように置き換えて考えることにしました。
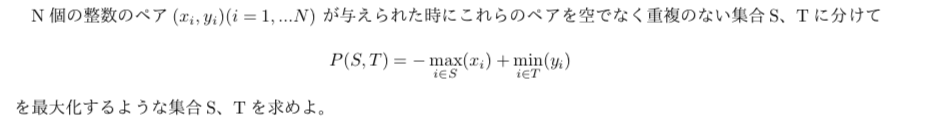
少し考えて、AGCの解説でいっている「この問題の解は。。。」の部分は上の問題でいうと以下のことをいっているのだとわかりました。
考察
上記の命題が正しいか図で直感的に考えてみました。上の問題は下のようなグラフで考えた時、
XY平面に存在するN個の点を2つの集合SとT に分け、Sについてのxの最大値X、Tについてのyの最小値をYとするときP=Y-Xを最大にするような集合S,Tを考えることに等しい。x=Xをグラフの縦点線、y=Yをグラフの横点線で考えると(X,Y)は縦横点線の交点になる。このとき青の点は集合Sに属さないと(X,Y)が変化する点、赤は集合Tに属さないと(X,Y)が変化する点、紫は集合S,Tのどちらに含めても（X,Y)に影響しない点になります。
点線が交差する点の右下の範囲$(x>X, y<Y)$の領域には点が存在できない（そのような点はS,Tのどちらに入れてもX,Yのいずれかが変化してしまう）ので、イメージとしては点の部分に釘があって、右下から三角定規を差し込んで、三角定規の直角の頂点をなるべく左上に差し込める点を探すといった雰囲気になります。
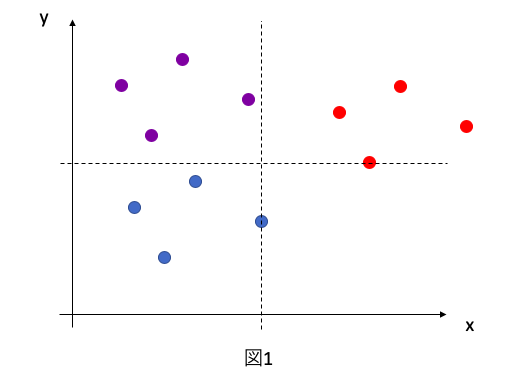
Y-Xが最大となる候補は例えば次のような分け方も候補になります。
つぎも候補といえば候補ですが明らかに図１のケースの方が評価が良いので選ばれる可能性はありません。
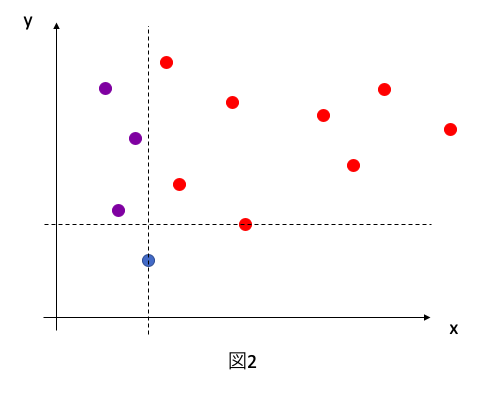
さて紫色の点はSとTのどちらに入れても目的とする値P=Y-Xはかわらないので、紫の点の数が0でない場合、同じY-Xを実現するSとTの組みわせは複数個あることになります。でも「紫のような点は全てSに含める」とすれば先ほどのような解法でY-Xの最大値を探せることがわかります。
所感
スキルが足りないので、解説に「〜〜です」といわれても、「え、なんで？」「必ずしもそうと言える？」などと感じる部分が多いです。解説のなかの「実は〜〜の部分は無視しても。。。」という部分も気にはなっているが追えてない。
修正
以下の部分まちがっていたで、「降順」を「昇順」に変更しました。もとのAGCとの問題とは符号が違うので逆になります。
