前回まで
前回の記事でひとまずデータセットから重回帰モデルを作りました。
モデルの精度や、詳しい分析を無視すれば
以下のように数行で重回帰モデルを作る事が出来ました。
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
env_data = pd.DataFrame(boston.data,columns = boston.feature_names)#説明変数のロード
price_data = boston.target#目的変数のロード
lr = LinearRegression()
lr.fit(env_data,price_data)#説明変数と目的変数からモデル作成
# 実際に予測を行いたい場合は
# lr.predict("説明変数")で計算可能
ただ、このモデルを実際に使おうと思うなら、予測精度の問題が出てきます。
いきなり**「高精度なモデルを作るんだ!」**なんてモチベーションはありませんが
とりあえず現状のモデルが使い物になるのか見ていきます。
モデルの精度を確かめる
まず、前回は全てのenv_dataを使ってモデルを作りました
今回は以下の様にデータを5分割して、4個分で学習し1個分で精度を確認
これを5回繰り返し、予測精度を確認します。
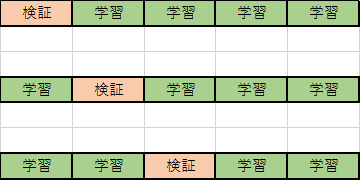
ボストン住宅価格のデータ数は506件だったので、400件を学習に使い、100件で精度検証をする事になります。
**交差検証(Cross-Validation)**っていう方法みたいです。
実際にやってみる
今回はcross_val_scoreという関数を使います。
モデルの評価を行う際には、他にもcross_validateという関数もありますが
今回はcross_val_scoreを使用します。
from sklearn.model_selection import cross_val_score
lr = LinearRegression()
print(cross_val_score(lr,env_data,price_data,cv = 5)
# [ 0.63861069 0.71334432 0.58645134 0.07842495 -0.26312455]
使い方は非常に簡単で、予測モデルのインスタンスを作って
目的変数と説明変数とセットで関数に渡してやるだけです。
ちなみに引数のcv = 5は分割数の指定で、5分割を設定しているという意味になります
その他の引数等、詳しいリファレンスはこちら
この数値はいいの?悪いの?
とりあえず#[ 0.63861069 0.71334432 0.58645134 0.07842495 -0.26312455]という値が取れました
この数値は決定係数という物で、R^2と表記されたりします。
この決定係数についてなんですが、複数の定義があるようで
cross_valid_scoreで返ってくるのは以下の定義の物だと思われます(違ってたらスイマセン・・・
y_i = i番目の物件価格\\
\hat{y_i} = i番目の予測価格\\
\bar{y} = 物件平均価格\\
\Large R^2 = 1 - {\frac{\sum_{i=1}^{n}(y_i - \hat{y_i})^2} { \sum_{i=1}^{n}(y_i - \bar{y})^2}}
数式はややこしいかもしれませんが、例え話をすれば
あなたはボストンに物件を持っているとします、しかし評価額が分かりません。
物件の部屋数や地域の犯罪率等のデータを持って不動産鑑定士にいくらになるか相談しました。
鑑定士「よく分かりませんが、ボストンの物件平均価格は1億円なんで、そんなもんじゃないですか」
こいつが決定係数=0の状態です、説明変数も何も関係なく目的変数の平均を返してくるだけのモデルです。
決定係数は1に近ければ近い程良いモデルで、マイナスになるとこのポンコツ鑑定士以下の存在になります。
決定係数がいくら以上あれば**使い物になる!**という基準は、使用者が決める事ですが
0.5程度あれば使い物になるという記述を見たことがあります。
その基準で行けば5回の交差検証の内、前半3回は概ねOKですが
後半2回は非常に精度の悪い結果となっている、と言えるかと思います
次回へ
次回は何故、交差検証の結果、後半2回の精度が著しく悪いのか
それを実際のデータを見ながら考えていきたいと思います。
お願い
機械学習初心者が勉強がてらの備忘録として投稿しています。
間違っている点等、お気づきの事がありましたらご指摘頂けますと誠に幸いです。