前回まで
前回の記事でscikit-learnライブラリで提供されている
ボストンの『住宅価格』と、『住宅の環境データ』をインポートして、相関性を見たりしました。
今回はそれぞれの『住宅の環境データ』、例えば犯罪率が『住宅価格』に対して、どのような影響を持っているか
それらを具体的に計算で数値化し、『住宅の環境データ』だけで『住宅価格』を予測出来る計算式を求めます。
ここからは『住宅価格』と『住宅の環境データ』を、それぞれ以下の様に記載します
『住宅価格』 = 目的変数
『住宅の環境データ』 = 説明変数
いざ計算
今回のケースでは目的変数に対して、説明変数は以下の13種ありました
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT |
|---|
なので、今回のケースでは『重回帰分析』を行います。
scikit-learnで重回帰分析を行う場合、一番カンタンなのは恐らく
LinearRegressionクラスを使用する方法です
前回の繰り返しになりますが、まず各種ライブラリとデータセットのインポートを行います。
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
boston = load_boston()
env_data = pd.DataFrame(boston.data,columns = boston.feature_names)
price_data = boston.target
で、次に計算を行ってくれるインスタンスを作ります。
lr = LinearRegression(fit_intercept = True)
引数のfit_interceptははデフォルトでTrueなので、態々指定しなくてもOKです。
また他にも以下のような引数があります
| 引数名 | データ型 | デフォルト | 内容 |
|---|---|---|---|
| fit_intercept | bool | True | バイアス(切片)を計算するかどうか(Trueで計算する) |
| normalize | bool | False | 説明変数を自動で正規化する(標準化ではない) |
| copy_X | bool | True | 引数で与える説明変数を上書きするか否か(Falseなら上書き) |
| n_jobs | int or NONE | NONE | 計算に使用するCPUコア数を指定する。NONEは1個、-1指定で全コア |
あとはインスタンスlrに目的変数と説明変数を与えればいいだけです
※説明変数の標準化等は次回以降に・・・
lr.fit(env_data,price_data)
これでlrの中に説明変数から目的変数を導き出す係数が計算され保持されます。
つまりlrに説明変数を入れてやると、その説明変数の値に応じて、それらしい目的変数(物件価格)を出力します。
とりあえずこれで目的としていた計算式(モデル)を作る事が出来ました。
試しにenv_dataをこの計算式に入れて、結果を見てみましょう
※モデルの精度検証ではないので、同じデータセットを使います。
forecast = lr.predict(env_data)
print(forecast[:10])
"""
予想結果10個分
30.00821269
25.0298606
30.5702317
28.60814055
27.94288232
25.25940048
23.00433994
19.5347558
11.51696539
18.91981483...
"""
数字だけ見てもピンと来ないので、実際の答えであるprice_dataとの差異を見てみましょう
ERROR = (forecast - price_data) / price_data
# 実際の価格に対して、平均誤差
print(np.mean(np.abs(ERROR))*100)
# 16.431734487377376(%)
# 最大の誤差
print(np.max(np.abs(ERROR))*100)
# 161.18584774173794(%)
ヒストグラムにすると以下みたいな感じです。
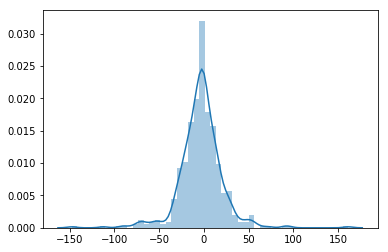
果たしてこれが精度の良いモデルなのかどうか、というのは疑問ですが
以上のような流れで、scikit-learnを用いて簡単に重回帰分析が出来ました。
モデルの中身を見てみよう
LinearRegressionクラスのインスタンスに目的変数と説明変数を与えて重回帰計算を行うと
coef_とintercept_というメンバ変数に計算結果が格納されます
| 変数名 | 内容 |
|---|---|
| coef_ | 回帰係数 |
| intercept_ | バイアス(切片) |
とりあえず実際の値を見てみましょう
print(lr.coef_)
"""
[-1.07170557e-01 4.63952195e-02 2.08602395e-02 2.68856140e+00
-1.77957587e+01 3.80475246e+00 7.51061703e-04 -1.47575880e+00
3.05655038e-01 -1.23293463e-02 -9.53463555e-01 9.39251272e-03
-5.25466633e-01]
"""
print(lr.intercept_)
# 36.49110328036137
このcoef_の値は説明変数のそれぞれに対応しています
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -1.07e-01 | 4.64e-02 | 2.09e-02 | 2.69e+00 | -1.78e+01 | 3.80e+00 | 7.51e-04 | -1.48e+00 | 3.06e-01 | -1.23e-02 | -9.53e-01 | 9.39e-03 | -5.25e-01 |
ここでは細かい数字は置いといて、符号にだけ注目してみます
| 符号がプラスの説明変数 | |
|---|---|
| ZN | 25,000 平方フィート以上の住居区画の占める割合 |
| INDUS | 小売業以外の商業が占める面積の割合 |
| CHAS | チャールズ川によるダミー変数 (1: 川の周辺, 0: それ以外) |
| RM | 住居の平均部屋数 |
| AGE | 1940 年より前に建てられた物件の割合 |
| RAD | 環状高速道路へのアクセスしやすさ |
| B | 町毎の黒人 (Bk) の比率を次の式で表したもの。 1000(Bk – 0.63)^2 |
| 符号がマイナスの説明変数 | |
|---|---|
| CRIM | 人口 1 人当たりの犯罪発生数 |
| NOX | NOxの濃度(窒素酸化物) |
| DIS | 5 つのボストン市の雇用施設からの距離 (重み付け済) |
| TAX | $10,000 ドルあたりの不動産税率の総計 |
| PTRATIO | 町毎の児童と教師の比率 |
| LSTAT | 給与の低い職業に従事する人口の割合 (%) |
符号がプラスの変数は入力が出力(物件価格)に対してプラスに作用し
符号がマイナスの変数は逆に出力に対してマイナスに作用するようになっています。
川の近くで高速道路へのアクセスが良い方が物件が高かったり
犯罪率が高く空気が悪いところは安い、というのは肌感覚で納得出来る部分もあるかと思います
次回へ
次回以降は、このモデルの精度をより高める事は出来ないか挑戦したり
LinearRegression以外のクラスを使用したりして、もう少しこのデータセットを見ていきます。
お願い
独学で機械学習を勉強しつつ、備忘録・理解の確認の為にQiitaに投稿しています。
間違った解釈や説明が多々あるかと思います。
お気づきになった方は、どうか優しくご指摘お願いいたします