今日は補間についてまとめておく。
参考のように線形補間は簡単なんだけど、その次の補間曲線も難しいわけではないので、今回は二次補間まで実際に計算して補間してみた。
一般的な補間公式はラグランジュ補間として、参考②のような公式が知られている。
ここではこの公式を使って、二次補間まで実施すると曲線も滑らかに補間できることを見る。
【参考】
①2点間の線形補間を計算する
②ラグランジュ補間
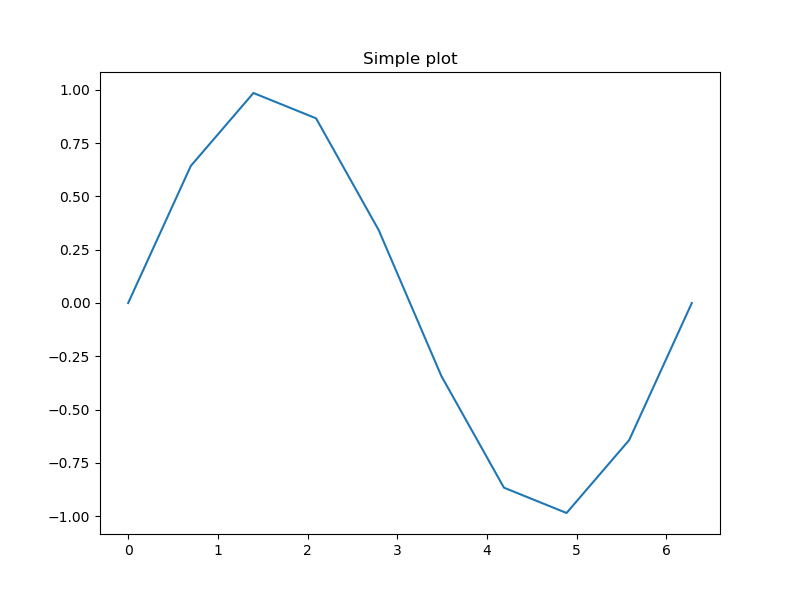
出だしは、昨日のサイン波のプロットから始めます。
import matplotlib.pyplot as plt
import numpy as np
pitch=10
x=np.linspace(0,2*np.pi,pitch)
y=np.sin(1.0*x)
plt.plot(x,y)
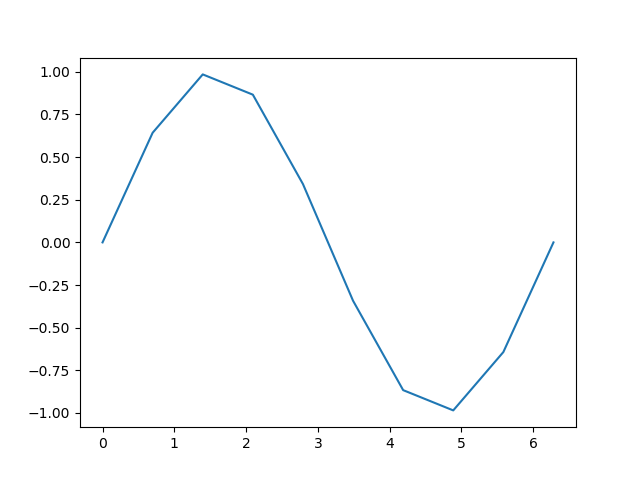
上記のあらあらな関数を以下の参考①の関数でポイントを二倍に増やす線形補間をする。
def interpolation(x0,y0,x1,y1,x):
return y0 + (y1 - y0) * (x - x0) / (x1 - x0)
sig=np.zeros(2*pitch-1)
sig[0]=y[0]
for i in range(1,2*pitch-1,1):
if i%2==0:
sig[i]=y[int(i/2)]
else:
sig[i] = interpolation(int(i/2),y[int(i/2)],int(i/2)+1,y[int(i/2)+1],int(i/2)+1/2)
x2=np.linspace(0,2*np.pi,2*pitch-1)
plt.plot(x2,sig)
sig4=np.zeros(4*pitch-3)
sig4[0]=y[0]
sig4[4*pitch-4]=y[pitch-1]
for i in range(1,4*pitch-4,1):
if i%4==0:
sig4[i]=y[int(i/4)]
else:
sig4[i] = interpolation(int(i/4),y[int(i/4)],int(i/4)+1,y[int(i/4)+1],int(i/4)+(i%4)/4)
x4=np.linspace(0,2*np.pi,4*pitch-3)
plt.plot(x4,sig4)
補間関数をラグランジュ補間を意識して、以下のように変形する。
def interpolation(x0,y0,x1,y1,x):
dn = (x0-x1)
return y0*(x-x1)/dn + y1*(x0-x)/dn
# Lagrange interpolation
# y0*(x-x1)/(x0-x1)+y1*(x-x0)/(x1-x0)
また、増やすポイント数もm個に一般化する。
そして、m=10の場合は以下のように計算してグラフ化される。
m=10
sigm=np.zeros(m*pitch-(m-1))
sigm[0]=y[0]
sigm[m*pitch-m]=y[pitch-1]
for i in range(1,m*pitch-m,1):
if i%m==0:
sigm[i]=y[int(i/m)]
else:
sigm[i] = interpolation(int(i/m),y[int(i/m)],int(i/m)+1,y[int(i/m)+1],int(i/m)+(i%m)/m)
xm=np.linspace(0,2*np.pi,m*pitch-(m-1))
plt.plot(xm,sigm)
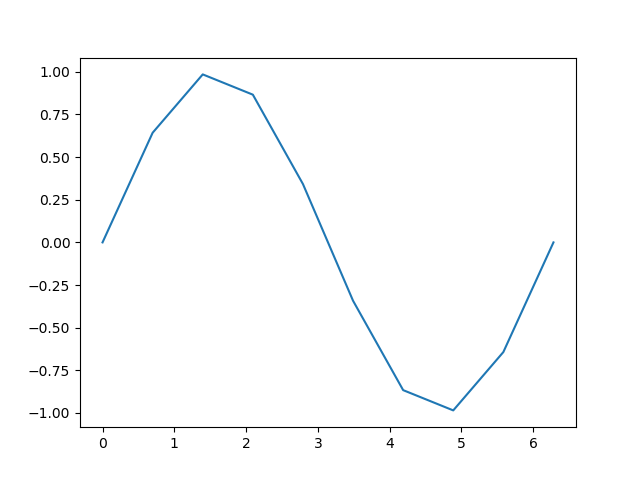
しかし以下のように、残念なことにポイント数を増やしても単に元の点の間を直線で近似しているので、丸みはでず近似精度は上がらない。
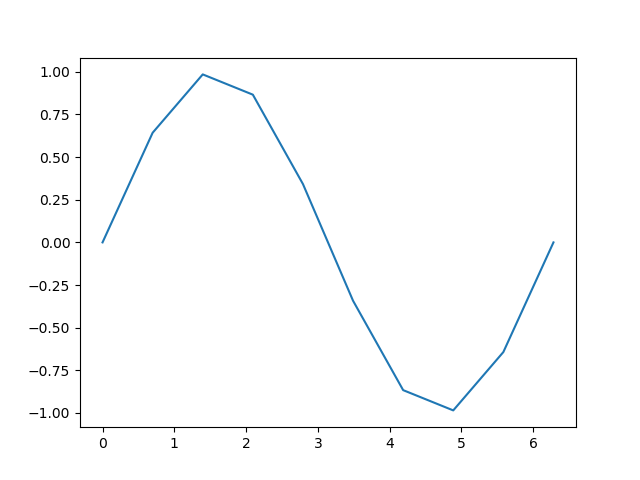
ということで、ラグランジュ補間公式を見つつ、二次補間を以下の関数でやってみる。線形近似からの大きな変更点は入力変数の組が3個必要だというところですが、あとは全く変わりません。
def interpolation2(x0,y0,x1,y1,x2,y2,x):
dn1 = (x0-x1)*(x0-x2)
dn2 = (x1-x2)*(x1-x0)
dn3 = (x2-x0)*(x2-x1)
return y0*(x-x1)*(x-x2)/dn1+y1*(x-x2)*(x-x0)/dn2+y2*(x-x0)*(x-x1)/dn3
ということで、この場合の計算は以下のように実施します。ここでもう少し工夫できますが、データの終端処理を先ほどの線形補間を利用しています。
もう少し、厳密に場合分けすればもっと精度があげられますが、データの終端の様子は現実データではいろいろなので、今回はこの程度にしておきます。
まず、4倍のポイントにした場合を計算します。
sigx2=np.zeros(4*pitch-3)
sigx2[0]=y[0]
sigx2[4*pitch-4]=y[pitch-1]
for i in range(1,4*pitch-4,1):
if i%4==0:
sigx2[i]=y[int(i/4)]
if i > 4*pitch-9:
sigx2[i] = interpolation(int(i/4),y[int(i/4)],int(i/4)+1,y[int(i/4)+1],int(i/4)+(i%4)/4)
else:
sigx2[i] = interpolation2(int(i/4),y[int(i/4)],int(i/4)+1,y[int(i/4)+1],int(i/4)+2,y[int(i/4)+2],int(i/4)+(i%4)/4)
グラフの範囲に注意して描画します。
x4=np.linspace(0,2*np.pi,4*pitch-3)
plt.plot(x4,sigx2)
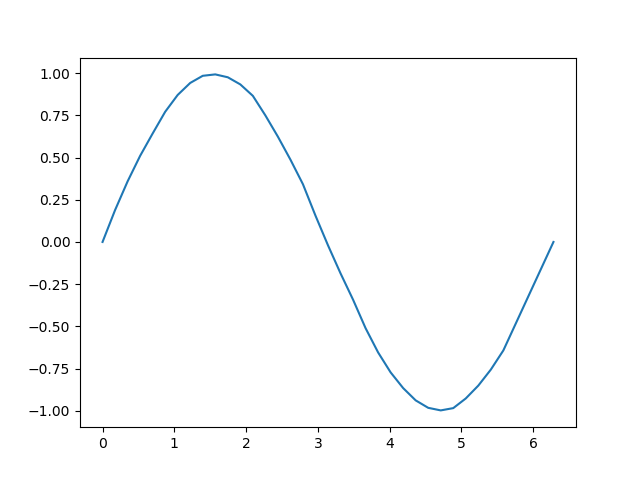
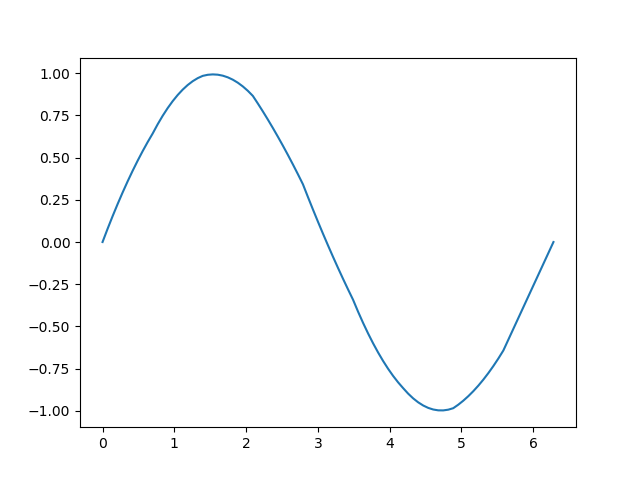
最後の所は直線近似なので仕方ないとして、その他の二次補間した部分は滑らかに変化しており、精度が上がっているのが分かります。
さらに、以下は一般化してmポイントの場合の計算の仕方です。
m=10として計算しています。
m=10
sigxm=np.zeros(m*pitch-(m-1))
sigxm[0]=y[0]
sigxm[m*pitch-m]=y[pitch-1]
for i in range(1,m*pitch-m,1):
if i%m==0:
sigxm[i]=y[int(i/m)]
if i > m*pitch-(2*m+1):
sigxm[i] = interpolation(int(i/m),y[int(i/m)],int(i/m)+1,y[int(i/m)+1],int(i/m)+(i%m)/m)
else:
sigxm[i] = interpolation2(int(i/m),y[int(i/m)],int(i/m)+1,y[int(i/m)+1],int(i/m)+2,y[int(i/m)+2],int(i/m)+(i%m)/m)
x4=np.linspace(0,2*np.pi,m*pitch-(m-1))
plt.plot(x4,sigxm)
精度を見る
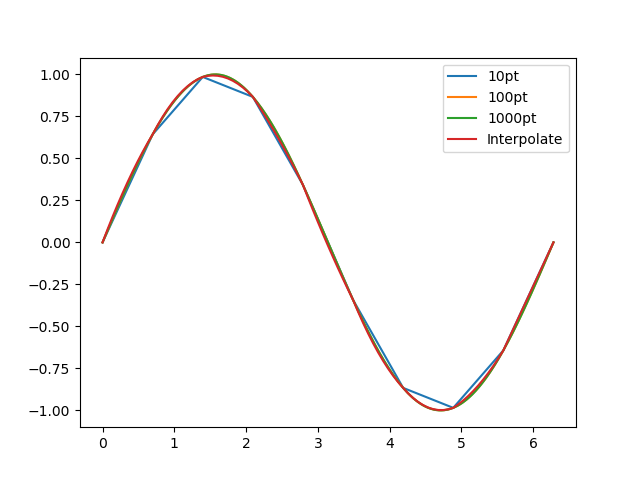
最後にサイン波を10pt,100pt,1000ptで計算して比較したグラフを示す。
10pt計算の10倍補間はかなりいい精度が出ているのが分かる。
まとめ
・線形補間をやってみたが、線形ゆえ精度は上がらない
・二次補間をやってみた。滑らかに補間できた
・ラグランジュ公式を使えば、さらに高次の補間もできるが、当面は二次補間で十分である
コード全体
import matplotlib.pyplot as plt
import numpy as np
def plot_signal(path,t1,sig,sig_name='default'):
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(t1, sig[:len(t1)])
ax.grid(True)
#plt.xlim([0, 1])
#plt.ylim([0, 5])
plt.savefig(path+"plot_signal_"+sig_name+".jpg", dpi=100)
plt.pause(1)
plt.close()
"""
def interpolation(x0,y0,x1,y1,x):
return y0 + (y1 - y0) * (x - x0) / (x1 - x0)
"""
def interpolation(x0,y0,x1,y1,x):
dn = (x0-x1)
return y0*(x-x1)/dn + y1*(x0-x)/dn
# Lagrange interpolation
# y0*(x-x1)/(x0-x1)+y1*(x-x0)/(x1-x0)
# https://risalc.info/src/lagrange-interpolation.html
def interpolation2(x0,y0,x1,y1,x2,y2,x):
dn1 = (x0-x1)*(x0-x2)
dn2 = (x1-x2)*(x1-x0)
dn3 = (x2-x0)*(x2-x1)
return y0*(x-x1)*(x-x2)/dn1+y1*(x-x2)*(x-x0)/dn2+y2*(x-x0)*(x-x1)/dn3
pitch=10
x=np.linspace(0,2*np.pi,pitch)
y=np.sin(10*x)
print(y)
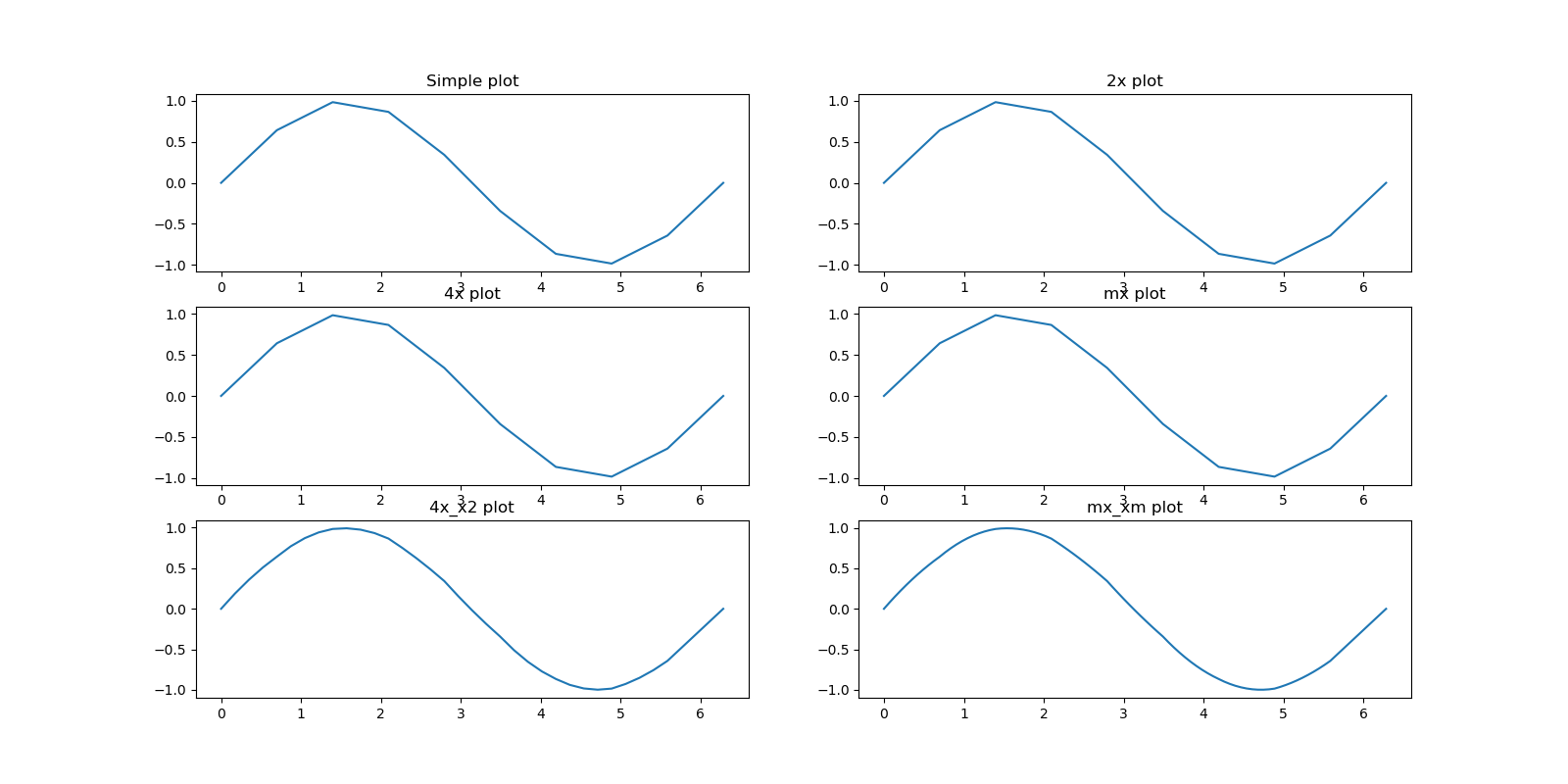
_, ax = plt.subplots(6)
plt.close()
fig=plt.figure(figsize=(16, 8))
ax[0]=fig.add_subplot(3,2,1)
ax[0].plot(x, y)
ax[0].set_title('Simple plot')
sig=np.zeros(2*pitch-1)
sig[0]=y[0]
# sig[2*pitch-1]=(y[pitch-1]*1+y[0]*1)/2
for i in range(1,2*pitch-1,1):
if i%2==0:
sig[i]=y[int(i/2)]
else:
sig[i] = interpolation(int(i/2),y[int(i/2)],int(i/2)+1,y[int(i/2)+1],int(i/2)+1/2)
print(sig)
x2=np.linspace(0,2*np.pi,2*pitch-1)
ax[1]=fig.add_subplot(3,2,2)
ax[1].plot(x2, sig)
ax[1].set_title('2x plot')
sig4=np.zeros(4*pitch-3)
sig4[0]=y[0]
sig4[4*pitch-4]=y[pitch-1]
for i in range(1,4*pitch-4,1):
if i%4==0:
sig4[i]=y[int(i/4)]
else:
sig4[i] = interpolation(int(i/4),y[int(i/4)],int(i/4)+1,y[int(i/4)+1],int(i/4)+(i%4)/4)
print(sig4)
x4=np.linspace(0,2*np.pi,4*pitch-3)
ax[2]=fig.add_subplot(3,2,3)
ax[2].plot(x4, sig4)
ax[2].set_title('4x plot')
m=10
sigm=np.zeros(m*pitch-(m-1))
sigm[0]=y[0]
sigm[m*pitch-m]=y[pitch-1]
for i in range(1,m*pitch-m,1):
if i%m==0:
sigm[i]=y[int(i/m)]
else:
sigm[i] = interpolation(int(i/m),y[int(i/m)],int(i/m)+1,y[int(i/m)+1],int(i/m)+(i%m)/m)
print(sigm)
xm=np.linspace(0,2*np.pi,m*pitch-(m-1))
ax[3]=fig.add_subplot(3,2,4)
ax[3].plot(xm, sigm)
ax[3].set_title('mx plot')
sigx2=np.zeros(4*pitch-3)
sigx2[0]=y[0]
sigx2[4*pitch-4]=y[pitch-1]
for i in range(1,4*pitch-4,1):
if i%4==0:
sigx2[i]=y[int(i/4)]
if i > 4*pitch-9:
sigx2[i] = interpolation(int(i/4),y[int(i/4)],int(i/4)+1,y[int(i/4)+1],int(i/4)+(i%4)/4)
else:
sigx2[i] = interpolation2(int(i/4),y[int(i/4)],int(i/4)+1,y[int(i/4)+1],int(i/4)+2,y[int(i/4)+2],int(i/4)+(i%4)/4)
print(sigx2)
x4=np.linspace(0,2*np.pi,4*pitch-3)
ax[4]=fig.add_subplot(3,2,5)
ax[4].plot(x4, sigx2)
ax[4].set_title('4x_x2 plot')
m=10
sigxm=np.zeros(m*pitch-(m-1))
sigxm[0]=y[0]
sigxm[m*pitch-m]=y[pitch-1]
for i in range(1,m*pitch-m,1):
if i%4==0:
sigxm[i]=y[int(i/m)]
if i > m*pitch-(2*m+1):
sigxm[i] = interpolation(int(i/m),y[int(i/m)],int(i/m)+1,y[int(i/m)+1],int(i/m)+(i%m)/m)
else:
sigxm[i] = interpolation2(int(i/m),y[int(i/m)],int(i/m)+1,y[int(i/m)+1],int(i/m)+2,y[int(i/m)+2],int(i/m)+(i%m)/m)
print(sigxm)
x4=np.linspace(0,2*np.pi,m*pitch-(m-1))
ax[5]=fig.add_subplot(3,2,6)
ax[5].plot(x4, sigxm)
ax[5].set_title('mx_xm plot')
plt.show()
おまけ
以下に、数値計算結果の値を掲載しておきます。
確かにきちんと計算しているようです。
>python interpolation.py
[ 0.00000000e+00 6.42787610e-01 9.84807753e-01 8.66025404e-01
3.42020143e-01 -3.42020143e-01 -8.66025404e-01 -9.84807753e-01
-6.42787610e-01 -2.44929360e-15]
[ 0.00000000e+00 3.21393805e-01 6.42787610e-01 8.13797681e-01
9.84807753e-01 9.25416578e-01 8.66025404e-01 6.04022774e-01
3.42020143e-01 -5.27355937e-16 -3.42020143e-01 -6.04022774e-01
-8.66025404e-01 -9.25416578e-01 -9.84807753e-01 -8.13797681e-01
-6.42787610e-01 -3.21393805e-01 -2.44929360e-15]
[ 0.00000000e+00 1.60696902e-01 3.21393805e-01 4.82090707e-01
6.42787610e-01 7.28292646e-01 8.13797681e-01 8.99302717e-01
9.84807753e-01 9.55112166e-01 9.25416578e-01 8.95720991e-01
8.66025404e-01 7.35024089e-01 6.04022774e-01 4.73021458e-01
3.42020143e-01 1.71010072e-01 -5.27355937e-16 -1.71010072e-01
-3.42020143e-01 -4.73021458e-01 -6.04022774e-01 -7.35024089e-01
-8.66025404e-01 -8.95720991e-01 -9.25416578e-01 -9.55112166e-01
-9.84807753e-01 -8.99302717e-01 -8.13797681e-01 -7.28292646e-01
-6.42787610e-01 -4.82090707e-01 -3.21393805e-01 -1.60696902e-01
-2.44929360e-15]
[ 0.00000000e+00 6.42787610e-02 1.28557522e-01 1.92836283e-01
2.57115044e-01 3.21393805e-01 3.85672566e-01 4.49951327e-01
5.14230088e-01 5.78508849e-01 6.42787610e-01 6.76989624e-01
7.11191638e-01 7.45393653e-01 7.79595667e-01 8.13797681e-01
8.47999696e-01 8.82201710e-01 9.16403724e-01 9.50605739e-01
9.84807753e-01 9.72929518e-01 9.61051283e-01 9.49173048e-01
9.37294813e-01 9.25416578e-01 9.13538343e-01 9.01660109e-01
8.89781874e-01 8.77903639e-01 8.66025404e-01 8.13624878e-01
7.61224352e-01 7.08823826e-01 6.56423300e-01 6.04022774e-01
5.51622248e-01 4.99221721e-01 4.46821195e-01 3.94420669e-01
3.42020143e-01 2.73616115e-01 2.05212086e-01 1.36808057e-01
6.84040287e-02 -5.27355937e-16 -6.84040287e-02 -1.36808057e-01
-2.05212086e-01 -2.73616115e-01 -3.42020143e-01 -3.94420669e-01
-4.46821195e-01 -4.99221721e-01 -5.51622248e-01 -6.04022774e-01
-6.56423300e-01 -7.08823826e-01 -7.61224352e-01 -8.13624878e-01
-8.66025404e-01 -8.77903639e-01 -8.89781874e-01 -9.01660109e-01
-9.13538343e-01 -9.25416578e-01 -9.37294813e-01 -9.49173048e-01
-9.61051283e-01 -9.72929518e-01 -9.84807753e-01 -9.50605739e-01
-9.16403724e-01 -8.82201710e-01 -8.47999696e-01 -8.13797681e-01
-7.79595667e-01 -7.45393653e-01 -7.11191638e-01 -6.76989624e-01
-6.42787610e-01 -5.78508849e-01 -5.14230088e-01 -4.49951327e-01
-3.85672566e-01 -3.21393805e-01 -2.57115044e-01 -1.92836283e-01
-1.28557522e-01 -6.42787610e-02 -2.44929360e-15]
[ 0.00000000e+00 1.88893852e-01 3.58989738e-01 5.10287657e-01
6.42787610e-01 7.71492879e-01 8.71397993e-01 9.42502951e-01
9.84807753e-01 9.93101814e-01 9.76069442e-01 9.33710639e-01
8.66025404e-01 7.50027372e-01 6.24027152e-01 4.88024742e-01
3.42020143e-01 1.56006788e-01 -2.00043783e-02 -1.86013355e-01
-3.42020143e-01 -5.11011106e-01 -6.54675637e-01 -7.73013737e-01
-8.66025404e-01 -9.38921225e-01 -9.83016890e-01 -9.98312399e-01
-9.84807753e-01 -9.27499667e-01 -8.51393615e-01 -7.56489595e-01
-6.42787610e-01 -4.82090707e-01 -3.21393805e-01 -1.60696902e-01
-2.44929360e-15]
[ 0.00000000e+00 7.78132970e-02 1.52618919e-01 2.24416867e-01
2.93207140e-01 3.58989738e-01 4.21764662e-01 4.81531911e-01
5.38291485e-01 5.92043385e-01 6.42787610e-01 6.97725736e-01
7.48055838e-01 7.93777914e-01 8.34891966e-01 8.71397993e-01
9.03295995e-01 9.30585972e-01 9.53267924e-01 9.71341851e-01
9.84807753e-01 9.91164549e-01 9.93469116e-01 9.91721454e-01
9.85921563e-01 9.76069442e-01 9.62165093e-01 9.44208514e-01
9.22199707e-01 8.96138670e-01 8.66025404e-01 8.20826454e-01
7.74027154e-01 7.25627503e-01 6.75627503e-01 6.24027152e-01
5.70826451e-01 5.16025399e-01 4.59623998e-01 4.01622246e-01
3.42020143e-01 2.66414538e-01 1.92409284e-01 1.20004380e-01
4.91998255e-02 -2.00043783e-02 -8.76082318e-02 -1.53611735e-01
-2.18014888e-01 -2.80817691e-01 -3.42020143e-01 -4.12655700e-01
-4.79239028e-01 -5.41770127e-01 -6.00248997e-01 -6.54675637e-01
-7.05050049e-01 -7.51372231e-01 -7.93642185e-01 -8.31859909e-01
-8.66025404e-01 -8.98639751e-01 -9.26646073e-01 -9.50044370e-01
-9.68834643e-01 -9.83016890e-01 -9.92591112e-01 -9.97557310e-01
-9.97915483e-01 -9.93665630e-01 -9.84807753e-01 -9.64140275e-01
-9.40465122e-01 -9.13782294e-01 -8.84091792e-01 -8.51393615e-01
-8.15687763e-01 -7.76974237e-01 -7.35253036e-01 -6.90524160e-01
-6.42787610e-01 -5.78508849e-01 -5.14230088e-01 -4.49951327e-01
-3.85672566e-01 -3.21393805e-01 -2.57115044e-01 -1.92836283e-01
-1.28557522e-01 -6.42787610e-02 -2.44929360e-15]