【重要】重大な計算ミスを発見したので、以下の記事はカオスアートとして鑑賞下さい。
一両日中に計算やり直し、別掲載予定です。
【ミスの内容】
本来以下のコードが正しいのですが、下のコードでやっていました。
※一部omegaとthetaを取り違えていました。
ちょっとやってみた感じではかなり異なるので、本稿はカオスアートとしてこのまま残そうと思います。そのつもりでお読みください。検証は別途記事にしたいと思います。
以下が正しい単振り子連結二重振り子としてのコードになります。
def doublePendulum(y, t, L, omegaJ,M):
theta1, omega1,theta2, omega2 = y
theta12=theta1 -theta2
#M=m2/(m1+m2)
#L=L2/L1
#omegaJ=g/L1
dydt = [omega1,
(omegaJ*L*(-np.sin(theta1)+M*np.cos(theta12)*np.sin(theta2))-M*L*(omega1*omega1*np.cos(theta12)+L*omega2*omega2)*np.sin(theta12))/(L-M*L*np.cos(theta12)*np.cos(theta12)),
omega2,
(omegaJ*(-np.sin(theta2)+np.cos(theta12)*np.sin(theta1))+(M*L*omega2*omega2*np.cos(theta12)+omega1*omega1)*np.sin(theta12))/(L-M*L*np.cos(theta12)*np.cos(theta12))]
return dydt
以下は一部omegaとthetaを取り違えたコードになります。
def doublePendulum(y, t, L1, L2,g,m1,m2):
theta1, omega1,theta2, omega2 = y
theta12=theta1 -theta2
M=m2/(m1+m2)
L=L2/L1
omegaJ=g/L1
dydt = [omega1,
(omegaJ*L*(-np.sin(theta1)+M*np.cos(theta12)*np.sin(theta2))-M*L*(theta1*theta1*np.cos(theta12)+L*theta2*theta2)*np.sin(theta12))/(L-M*L*np.cos(theta12)*np.cos(theta12)),
omega2,
(omegaJ*(-np.sin(theta2)+np.cos(theta12)*np.sin(theta1))+(M*L*theta2*theta2*np.cos(theta12)+theta1*theta1)*np.sin(theta12))/(L-M*L*np.cos(theta12)*np.cos(theta12))]
return dydt
ーーー
昨日の記事のとおり、ちょっと運動方程式が違うということで、二つの単振り子連結の二重振り子は同じような運動をするのかという問題。。。初期値鋭敏性や環境鋭敏性があるのに。。。
。。。カオスの構造は。。紋章は同じなのという疑問:今回はここを見たいと思います、
やったこと
(1)微分方程式の検証;二つの単振り子連結
(2)カオスアートで遊ぶ
(1)微分方程式の検証;二つの単振り子連結
前回の微分方程式は以下の通りでした
\theta_1'' = \frac{-g(2m_1 + m_2){\sin \theta_1} - m_2g{\sin (\theta_1 - 2\theta_2) -2{\sin \theta_{12}}}m_2(\theta_2'^2L_2+\theta_1'^2L_1{\cos\theta_{12})}}{L_1(2m_1+m_2-m_2{\cos2\theta_{12})}}
\theta_2'' = \frac{2{\sin\theta_{12}(\theta_1'^2L_1(m_1+m_2)+g(m_1+m_2){\cos\theta_1}}+\theta_2'^2L_2m_2{\cos\theta_{12})}}{L_2(2m_1+m_2-m_2{\cos2\theta_{12})}}
今回の微分方程式は以下のとおり
\theta_1'' = \frac{-g(m_1 + m_2){\sin \theta_1} + m_2g{\sin\theta_2\cos \theta_{12} -m_2{\sin \theta_{12}}}(\theta_2'^2L_2+\theta_1'^2L_1{\cos\theta_{12})}}{L_1(m_1+m_2-m_2{\cos^2\theta_{12})}}
\theta_2'' = \frac{{(L_1\theta_1'^2(m_1+m_2)+L_2\theta^2_2\cos\theta_{12})\sin\theta_{12}+g(m_1+m_2)(-\sin\theta_2+\cos\theta_{12}\sin\theta_1)}}{L_2(m_1+m_2-m_2{\cos^2\theta_{12})}}
両者を比較すると、やはり異なりますね。
導出も異なるからなんともだけど、ウワンのセンスでは、Lagragian求めて、そこからLagrange方程式で導出が馴染みです。
これでやるとまずL=K-Uとして、それぞれ
K=\frac{1}{2} (m_1+m_2)L_1^2\theta_1'^2+\frac{1}{2}m_2L_2^2\theta_2'^2+m_2L_1L_2\theta_1'\theta_2'\cos\theta_{12}
U=(m_1+m_2)gL_1(1-\cos\theta_1)+m_2gL_2(1-\cos\theta_2)
※以下のリンク先とはポテンシャルエネルギーの第二項の符号が違うんだけど、
。。。m_2の変化分はL_1の変化分とL_2の変化分は同じ符号で上記のとおり
【参考】
・二重振り子@カオス&非線形力学入門
ここまで出れば、普通に、極座標では以下のように
\frac{d}{dt}(\frac{∂ L}{∂\theta'})-\frac{∂ L}{∂\theta}=0
が運動方程式になる。ということで上式が得られる。
(2)カオスアートで遊ぶ
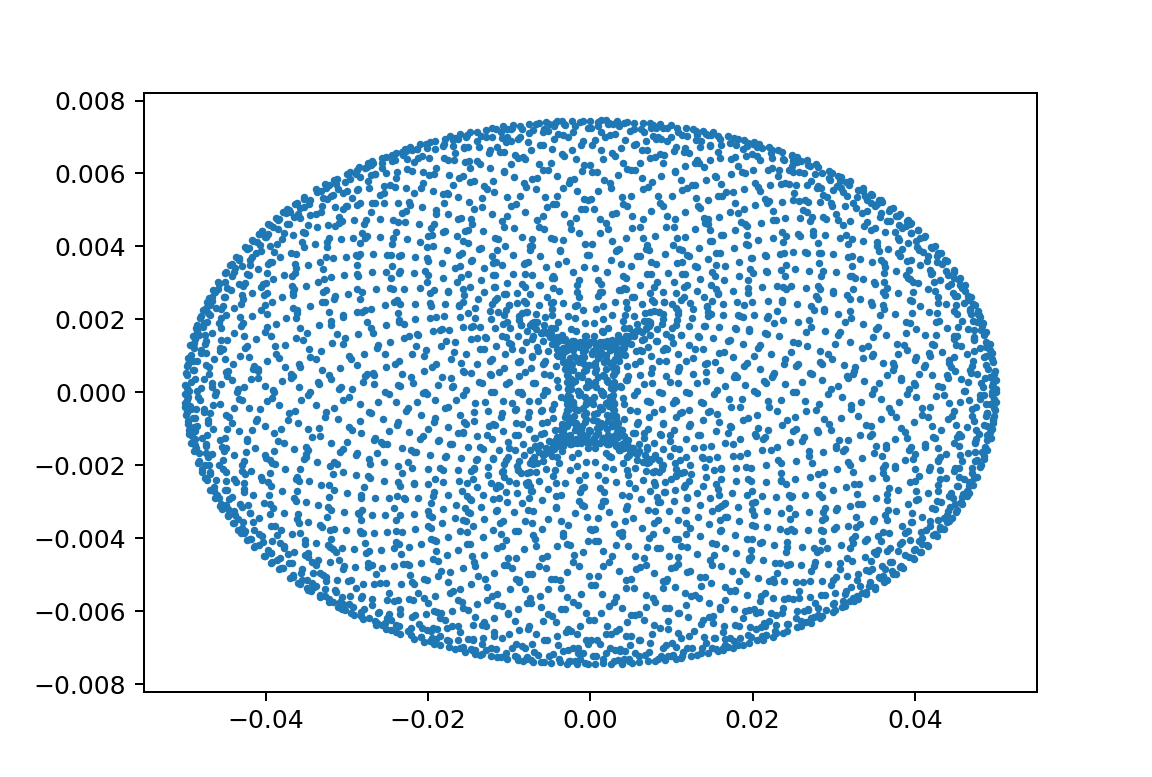
当然、ちょっと異なるカオスアート。。。
特に初期値が大きいと計算誤差が大きくて大まかにいうとy01=0.1ラジアン以上の初期値は計算誤差で計算できませんでした。
とはいえ、今回もかなり特徴的なカオスアートが描けました。
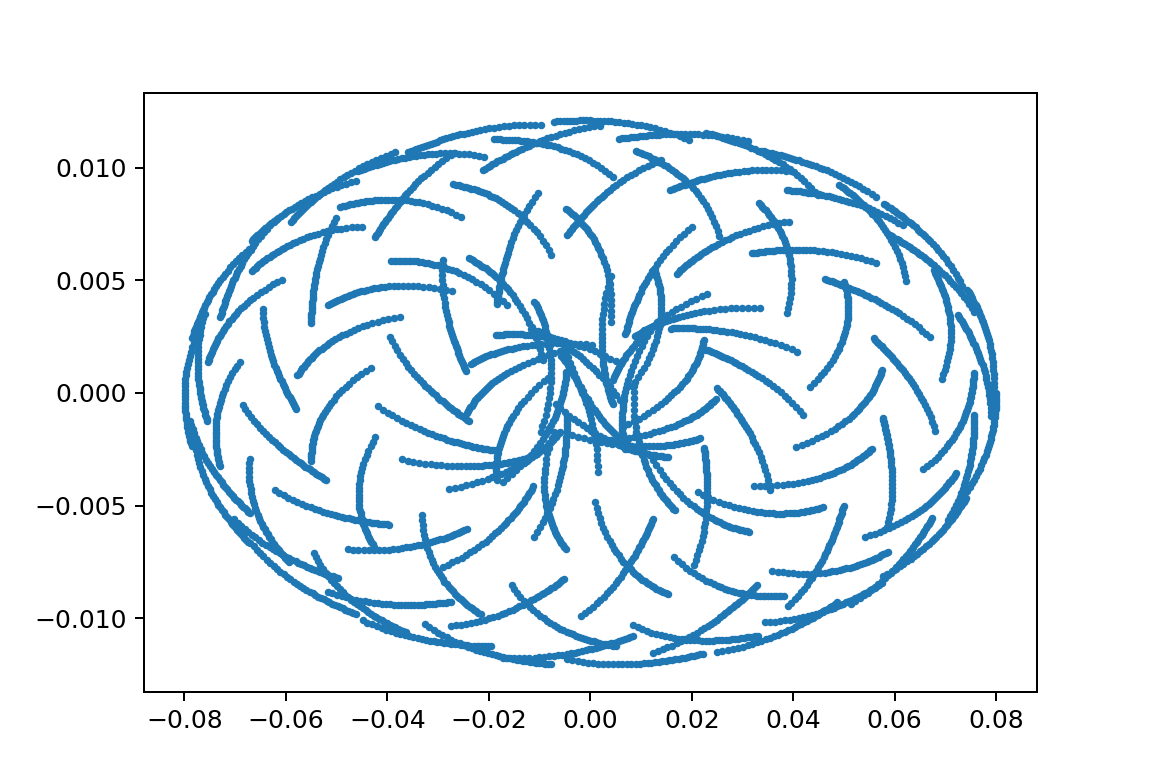
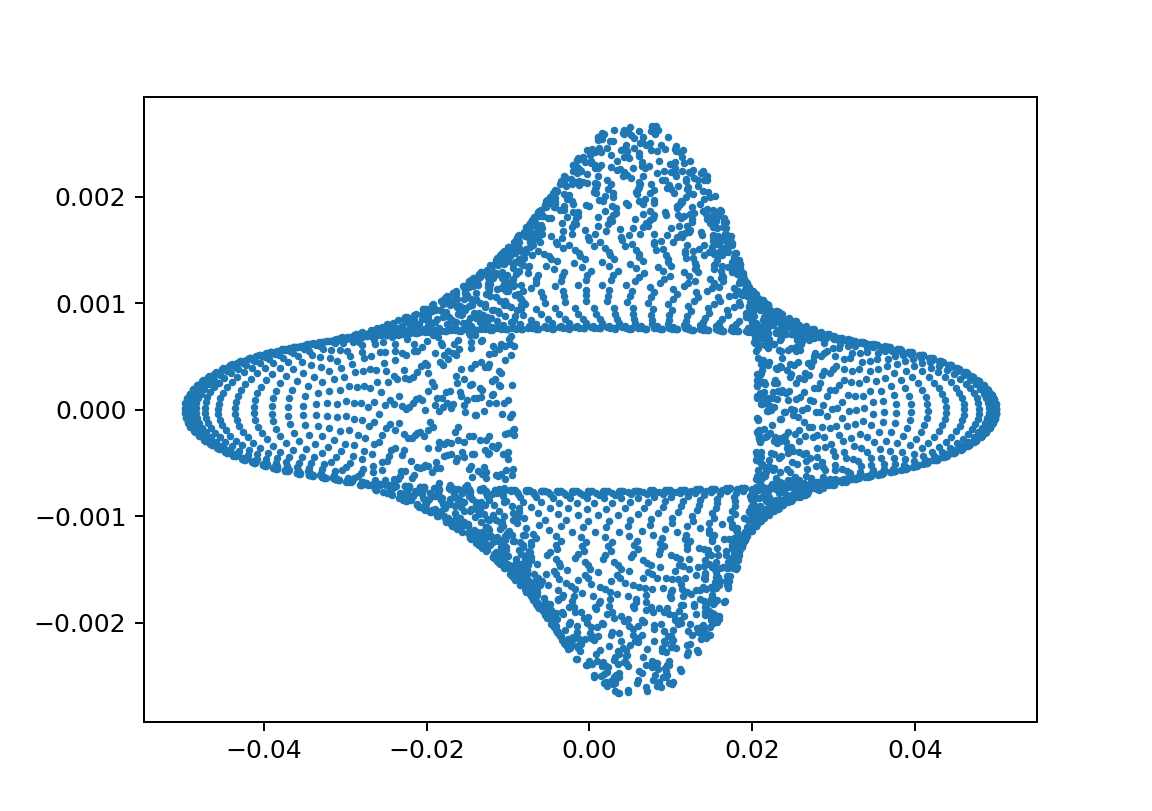
xp1_L1500L2495m110m21.75y010.4
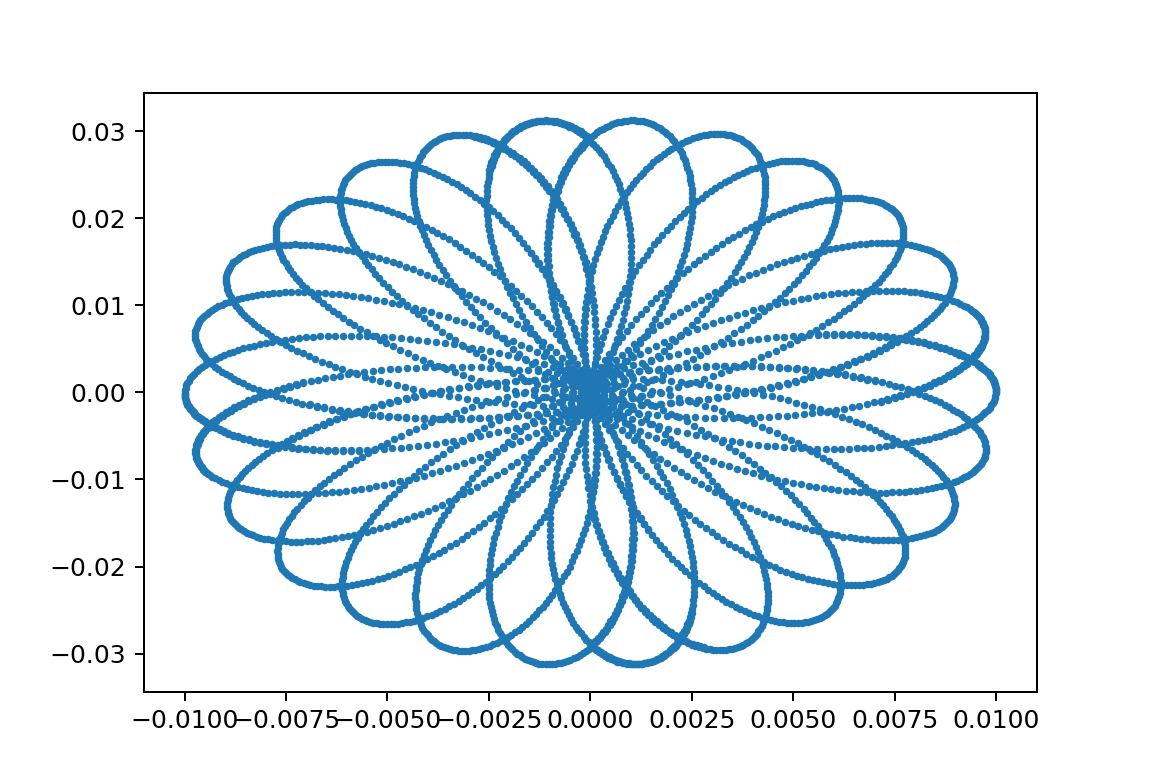
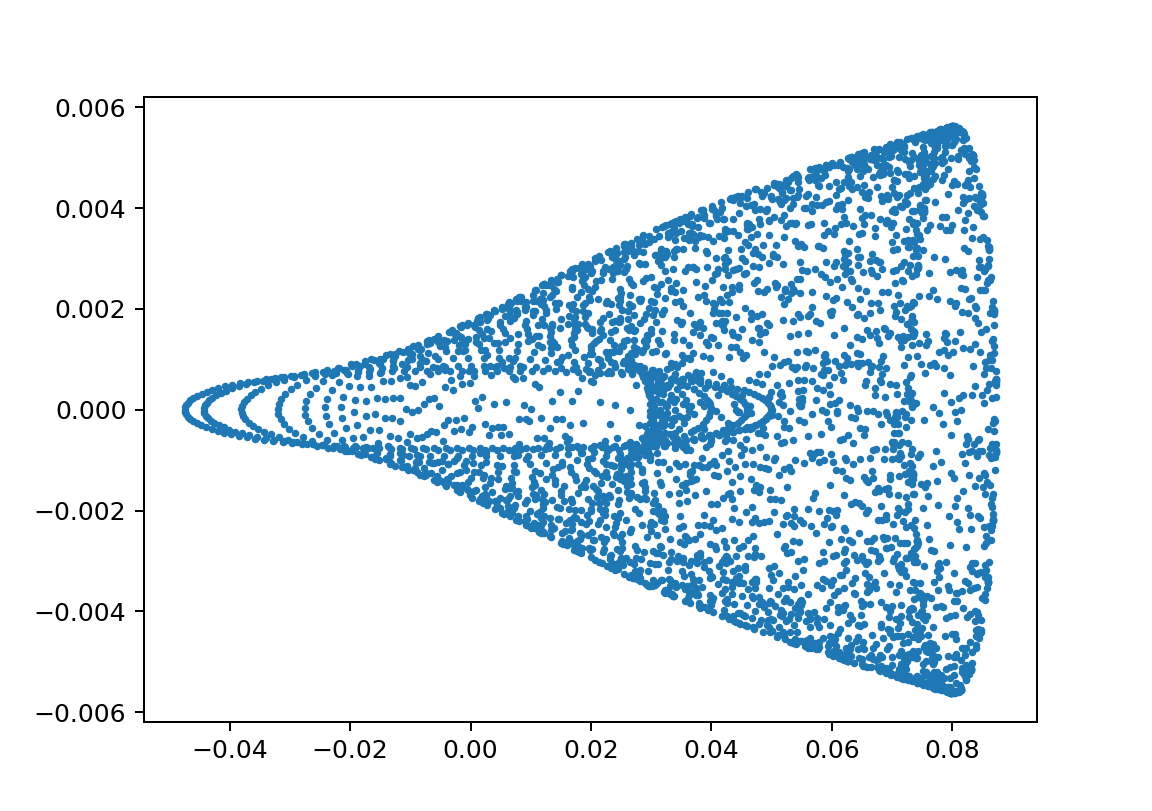
xp1_L150000L249999m110000m21000y010.08
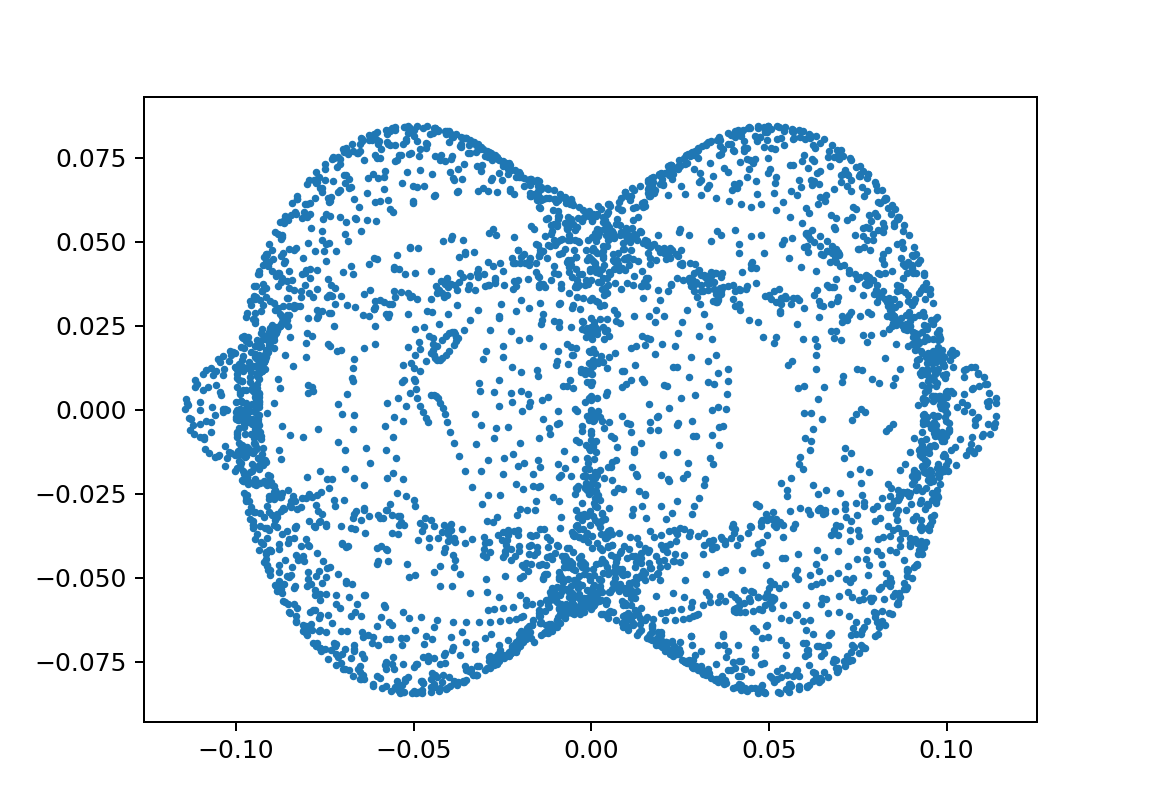
xp1_L150000L249999.5m110000m210000y010.08
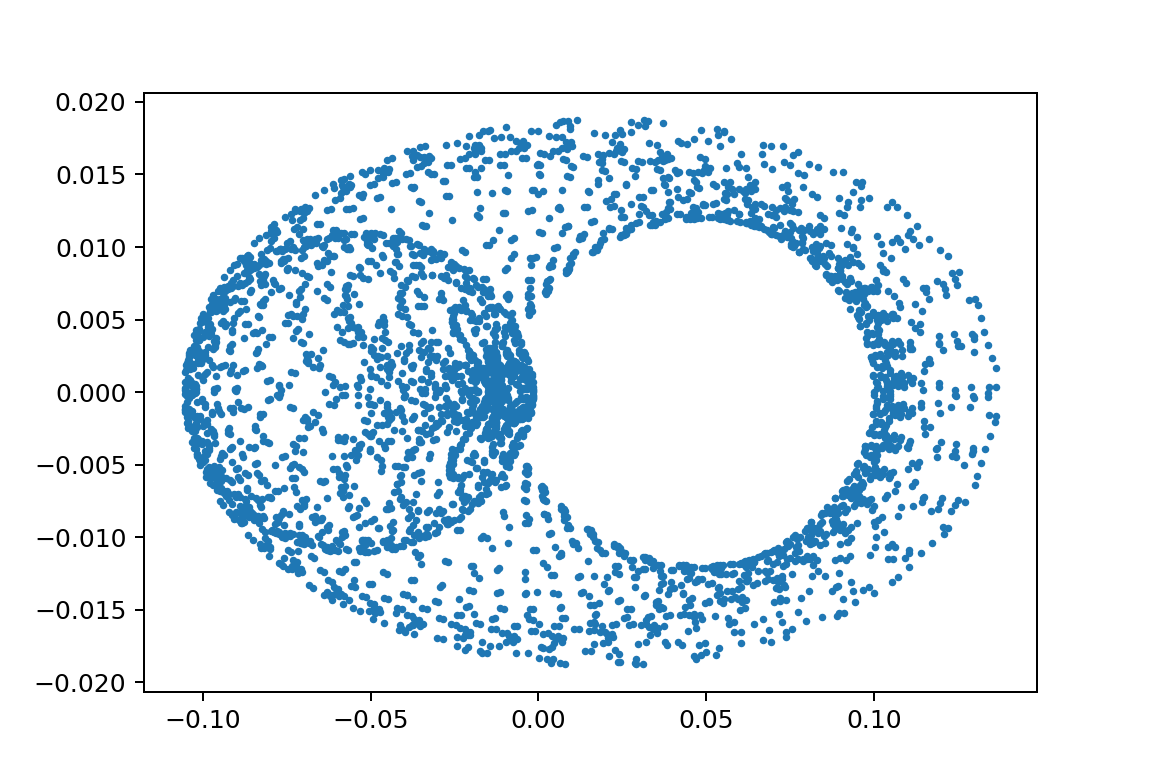
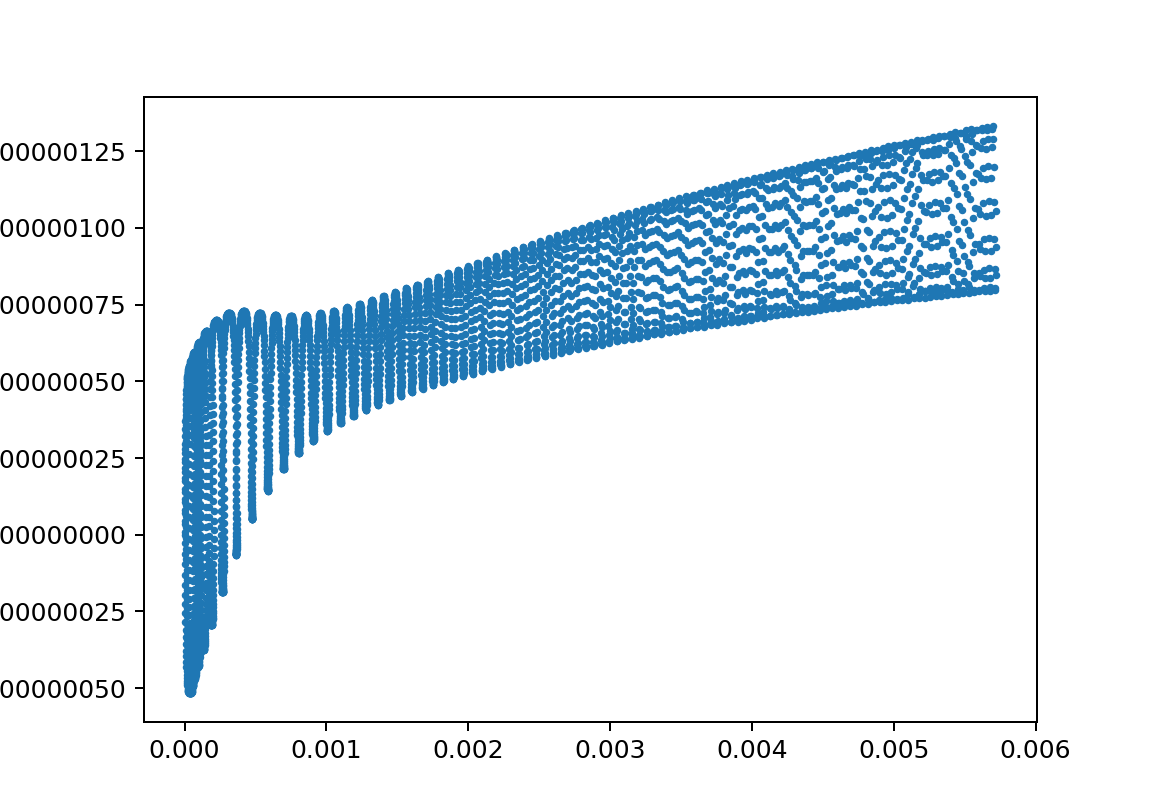
比較的前回と似ている絵
xp1_L150000L24750m11000m21020y010.005
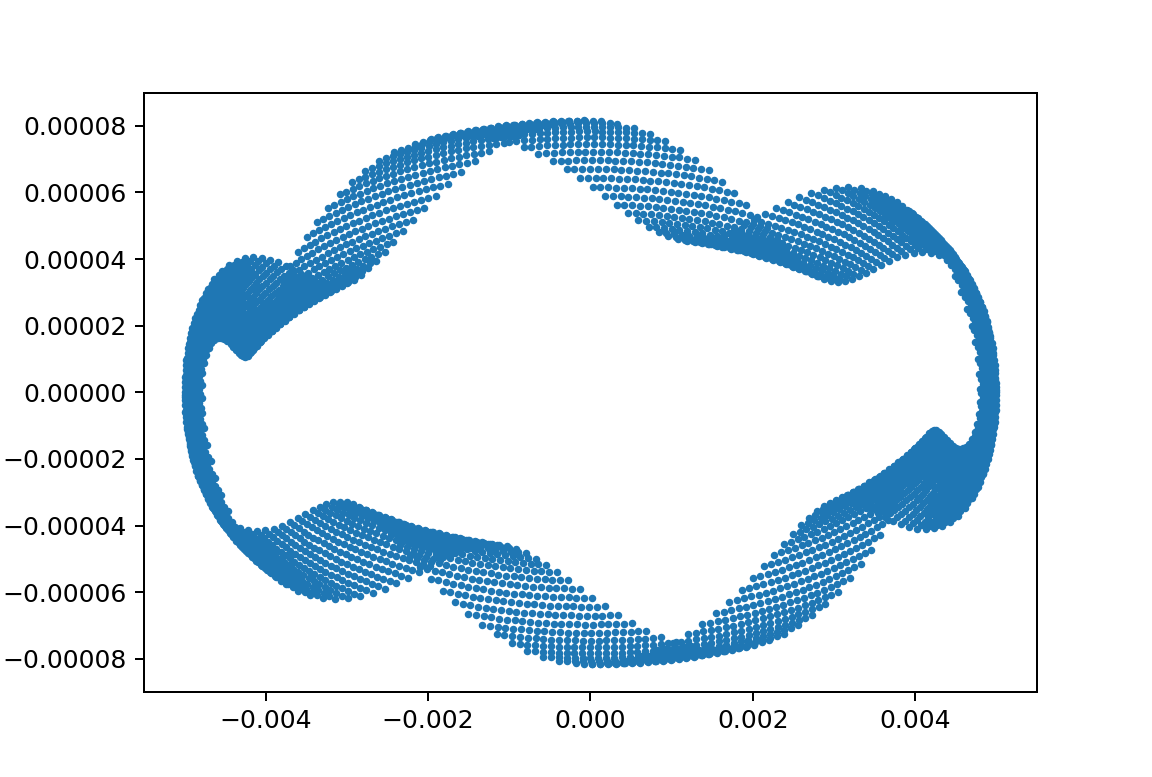
しかし、初期値を見ると二けたは小さい領域です。
xp1_L0.1M9.8e-05omegaJ0.0909y010.05
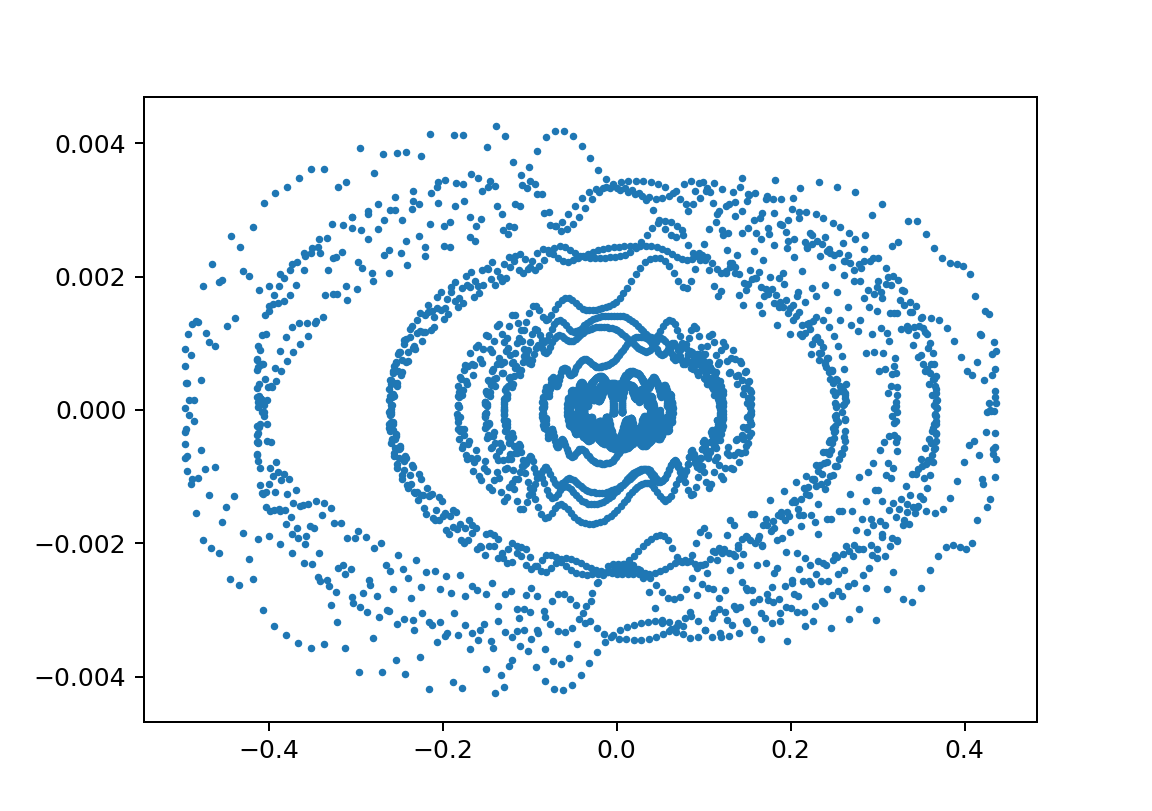
xp2_L0.1M9.8e-05omegaJ0.0909y010.05
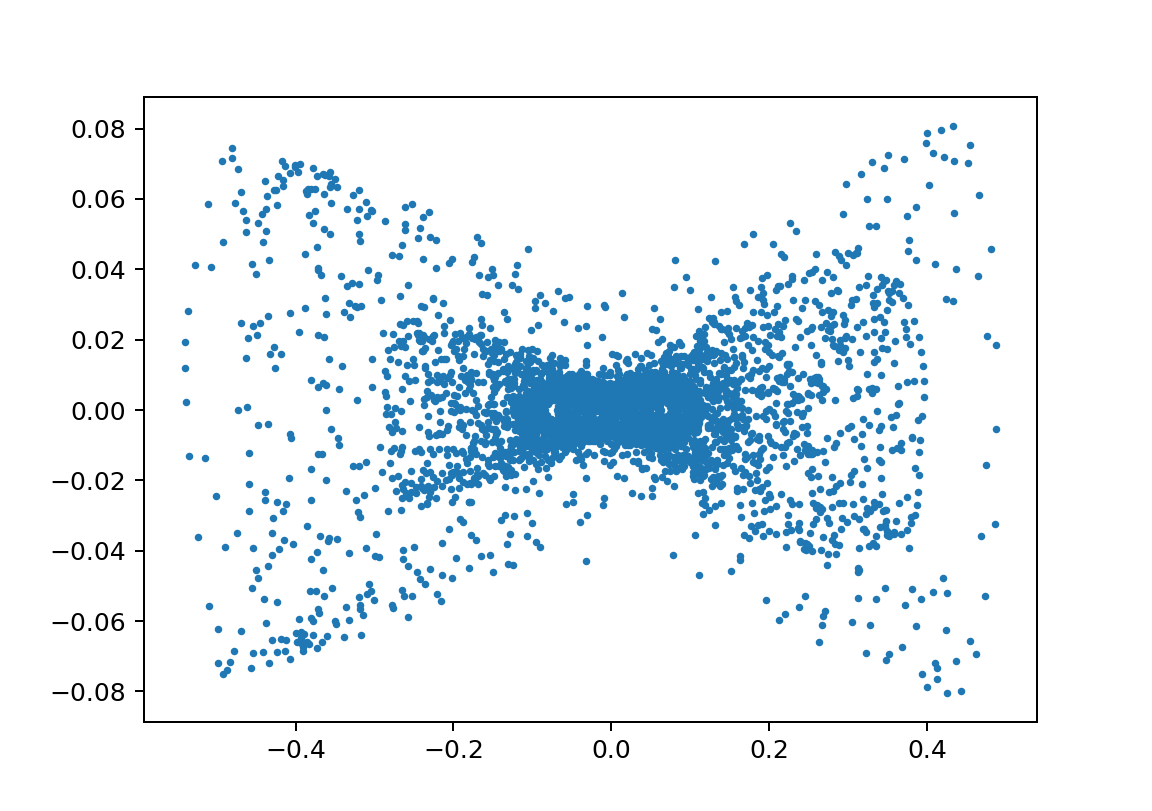
初期値の違いでかなり絵が違う
xp1_L150000L249999m110000m210000y010.05
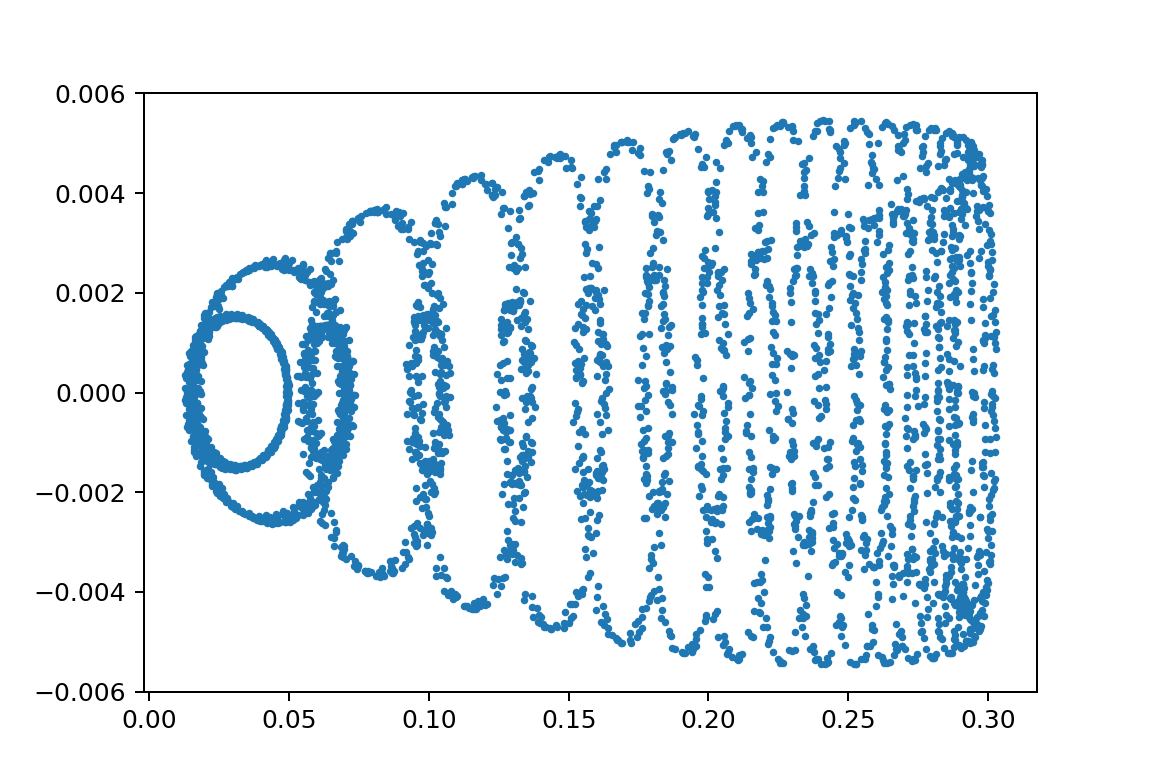
xp1_L150000L249999m110000m210000y010.01
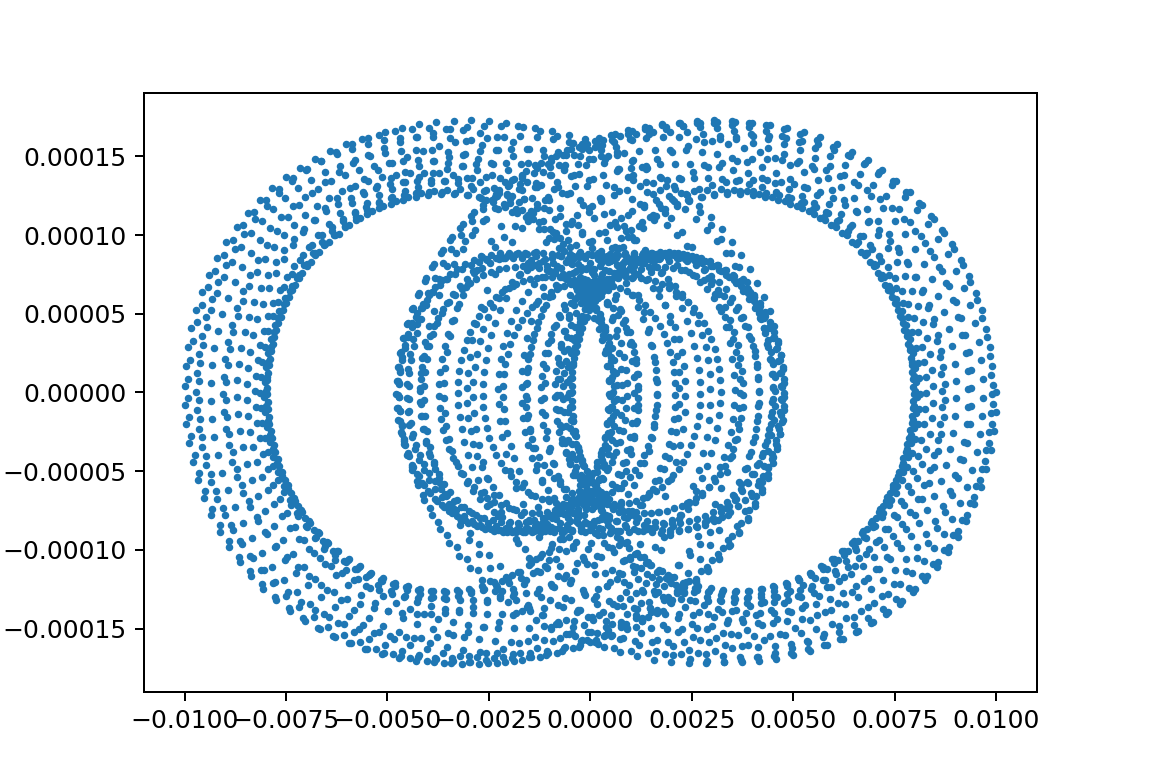
重りの違いでも!かなり違う
xp1_L150000L249900m110.0m21.75y010.0005
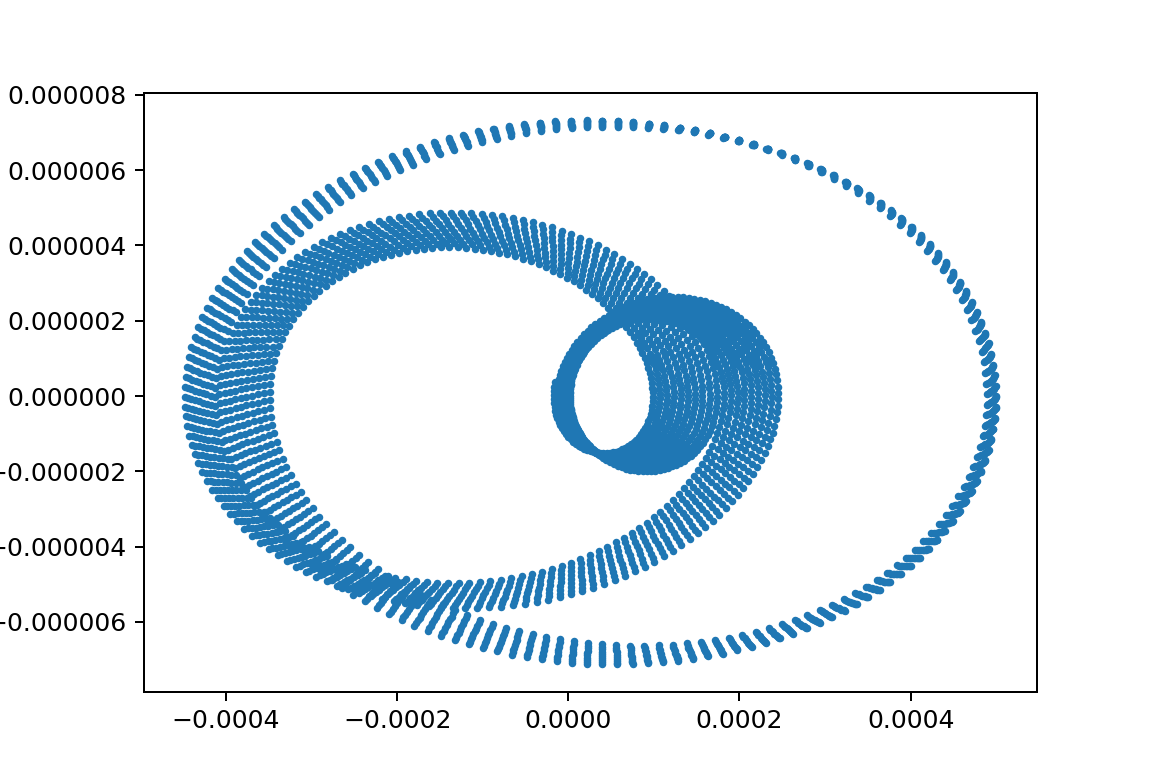
以下はリボンの絵をシステマティックにパラメータを変更して出てくる絵をコントールできた例
xp1_L150000L24750m11000m21020y010.005
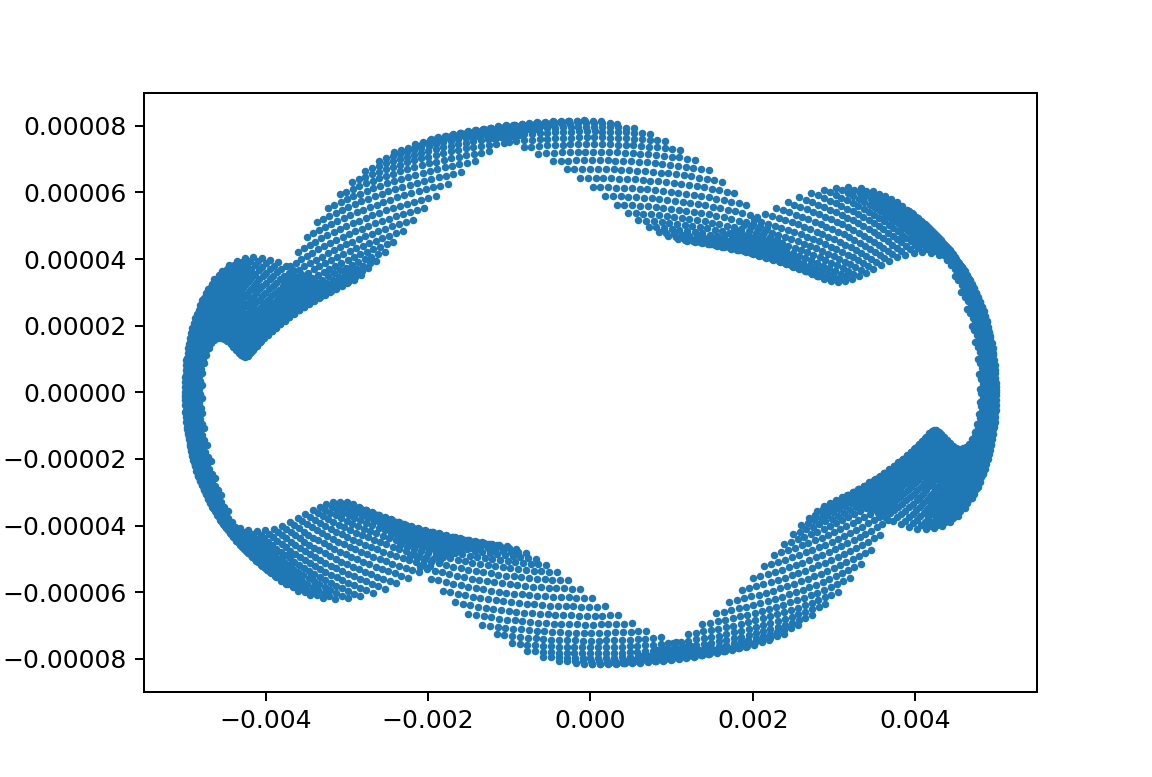
xp1_L150000L24750m11000m21030y010.005
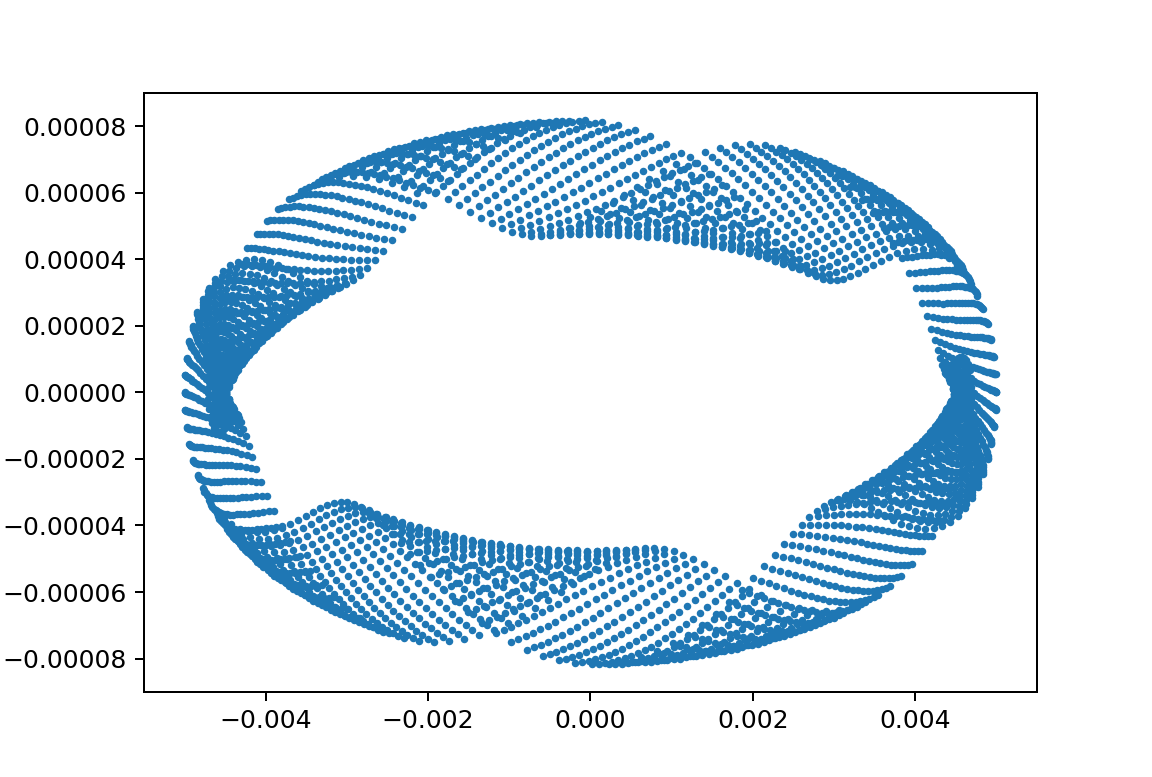
xp1_L150000L24750m11000m21035y010.005
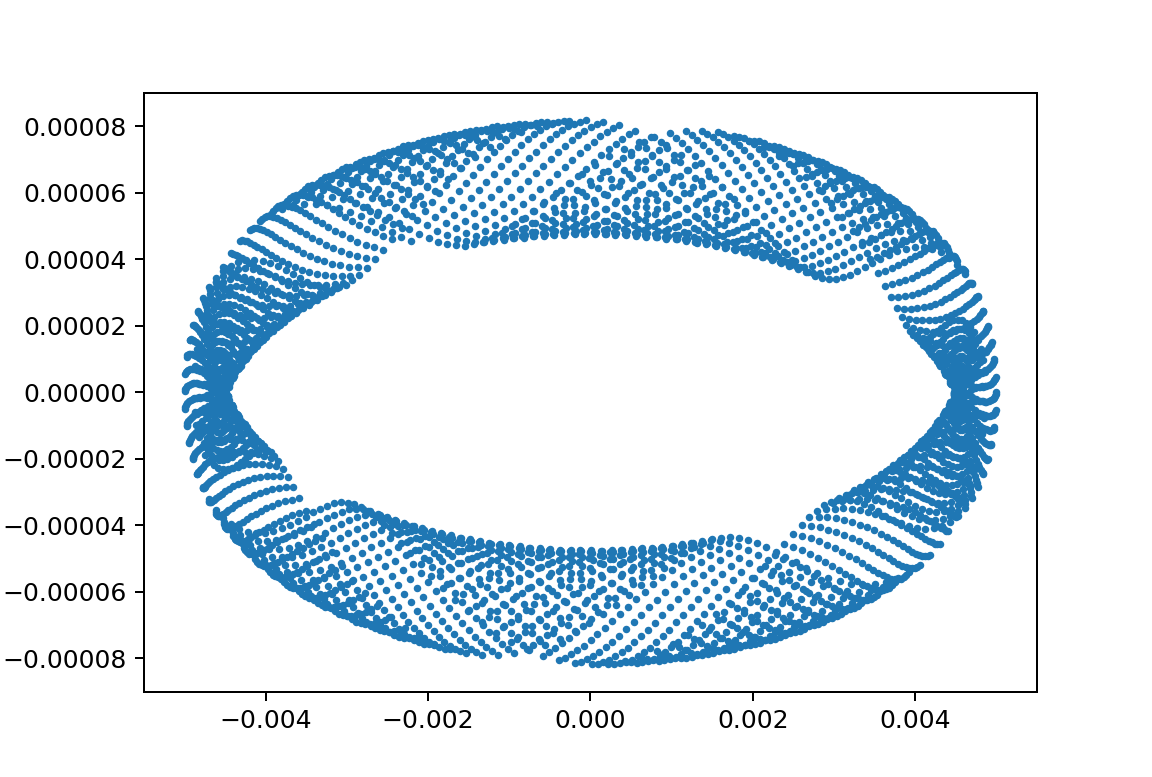
xp1_L150000L24750m11000m21050y010.005
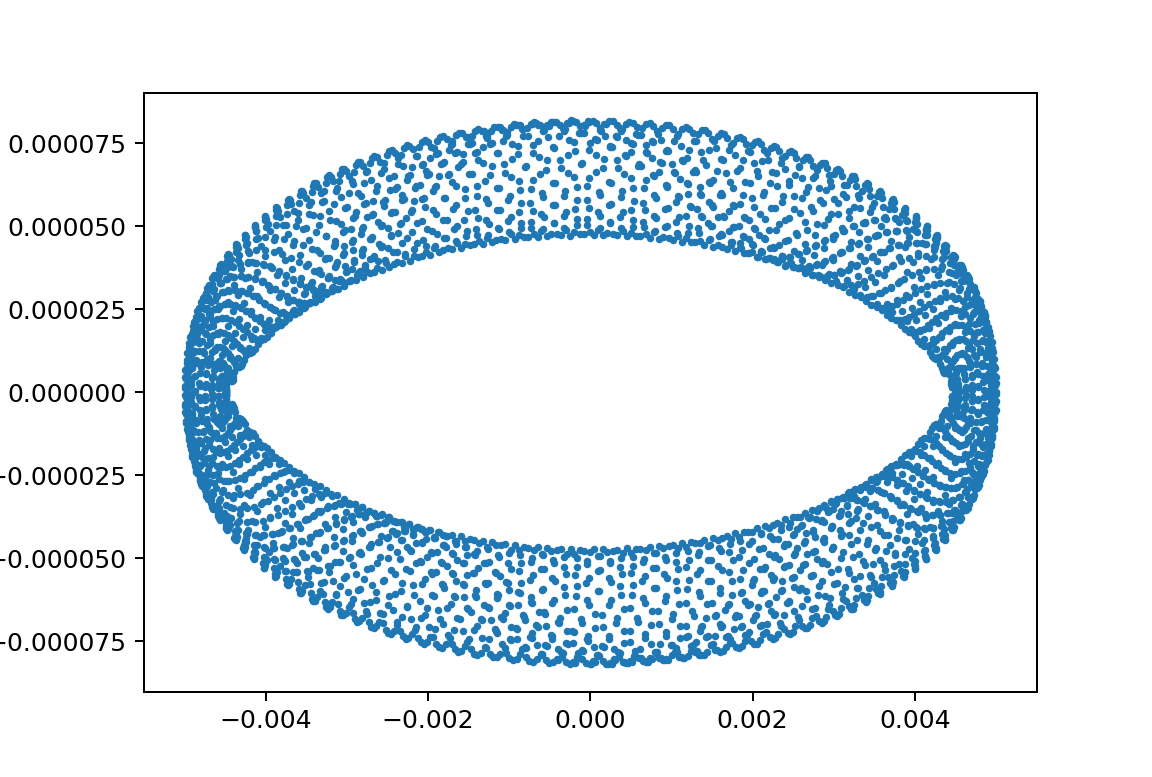
もう一つの例
xp1_L150000L249998m110000m210000y010.08
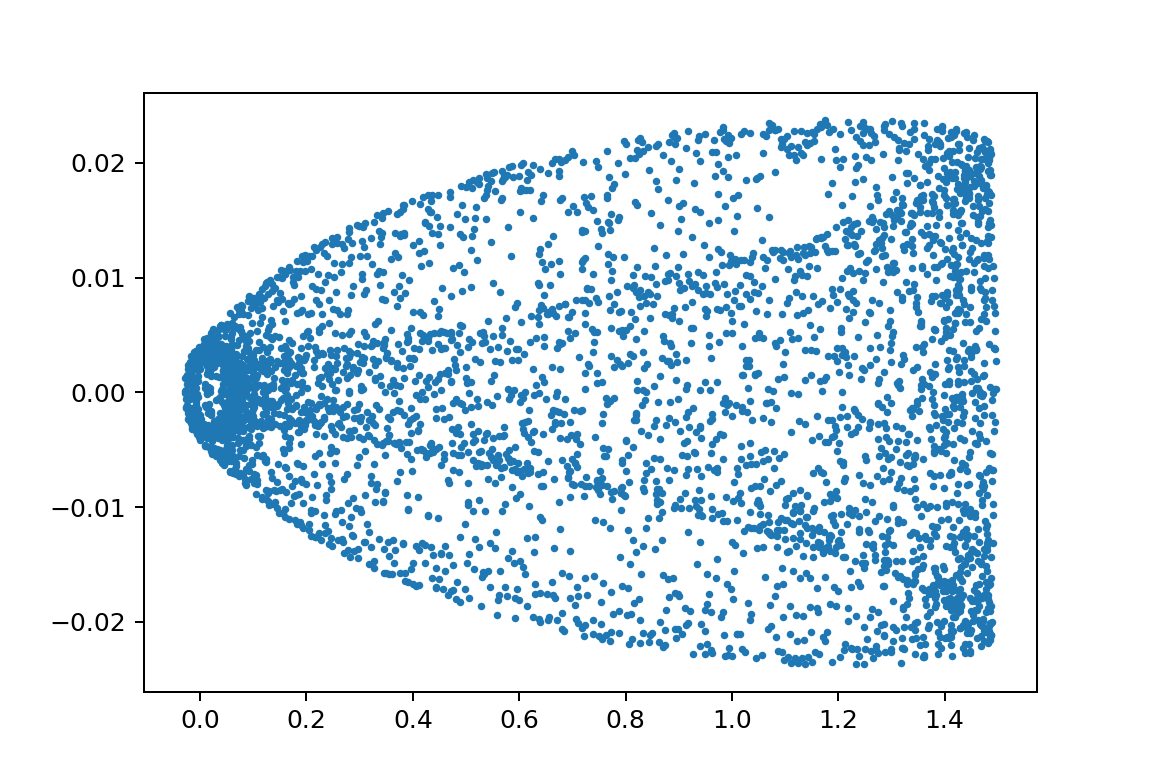
xp1_L150000L249999m110000m210000y010.08
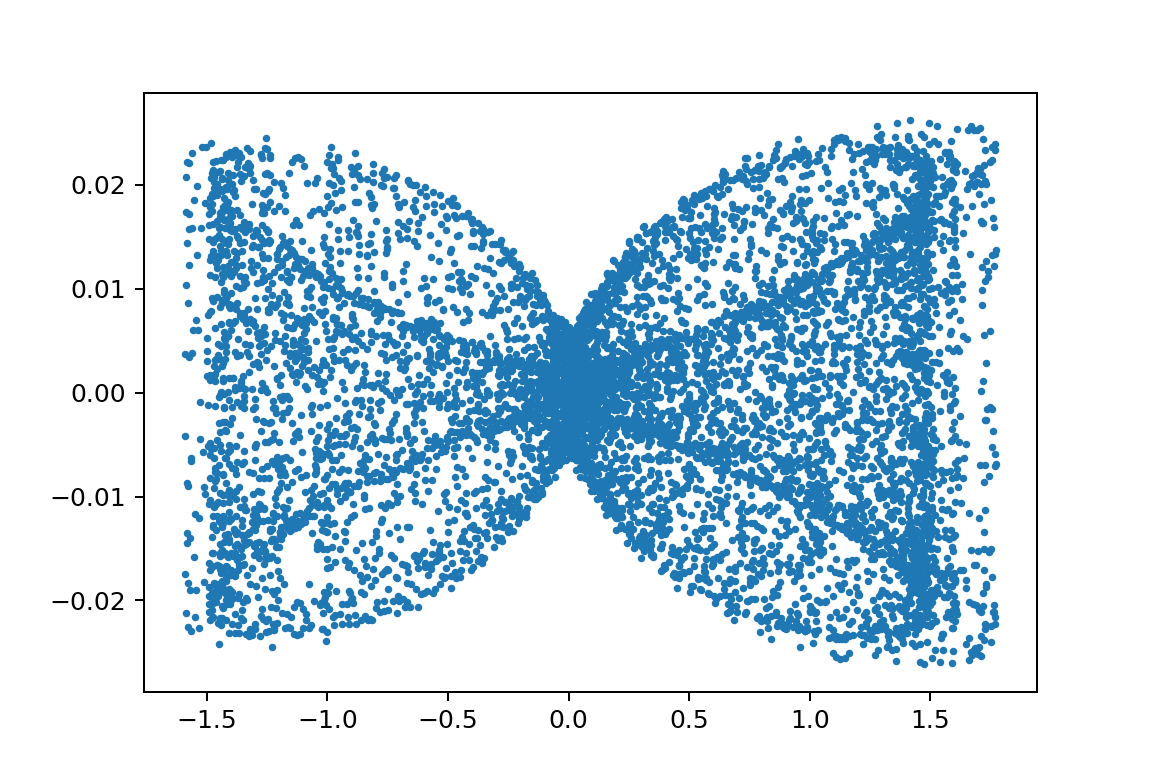
xp1_L150000L249999.5m110000m210000y010.08
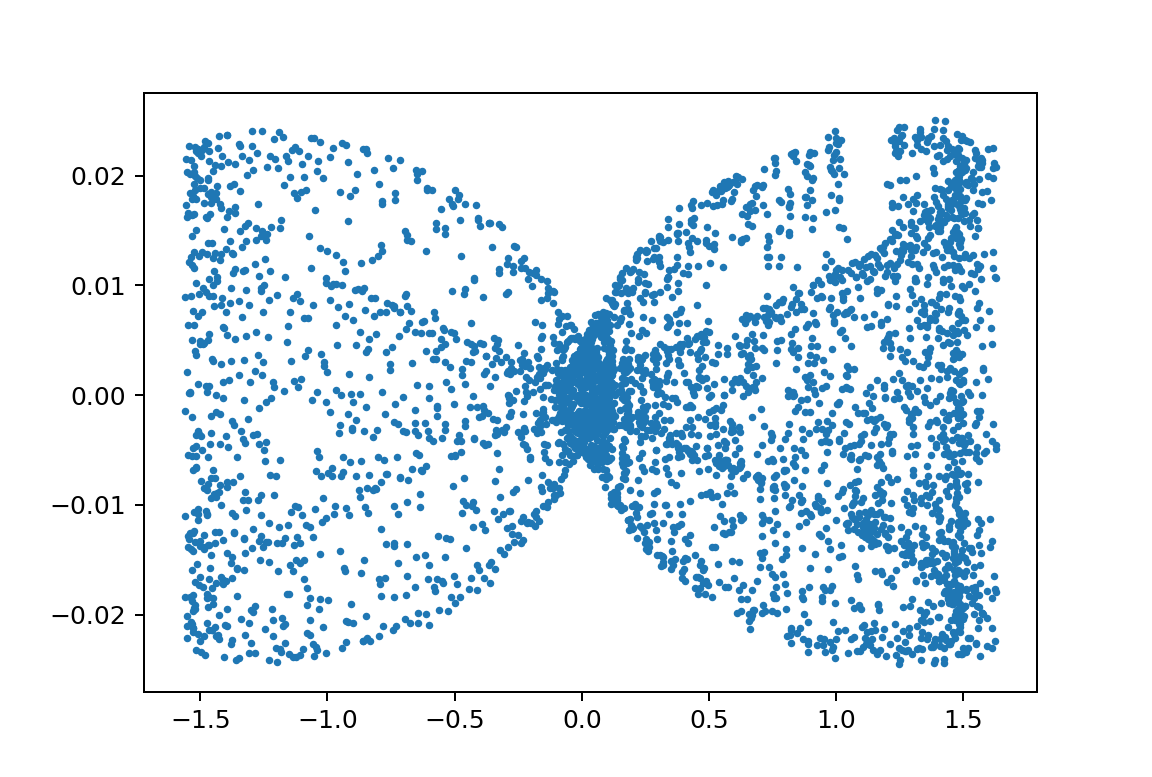
xp1_L150000L249999.9m110000m210000y010.08
振幅が小さければリボン
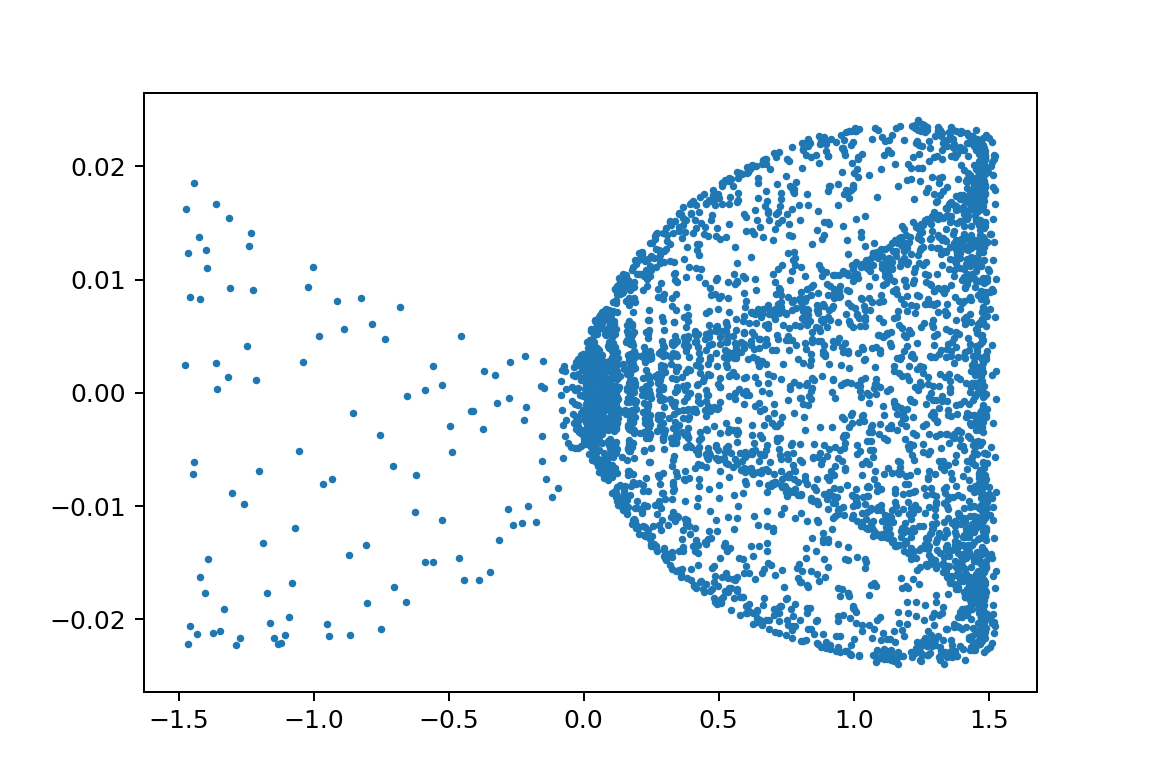
xp1_L150000L249999m110000m210000y010.01
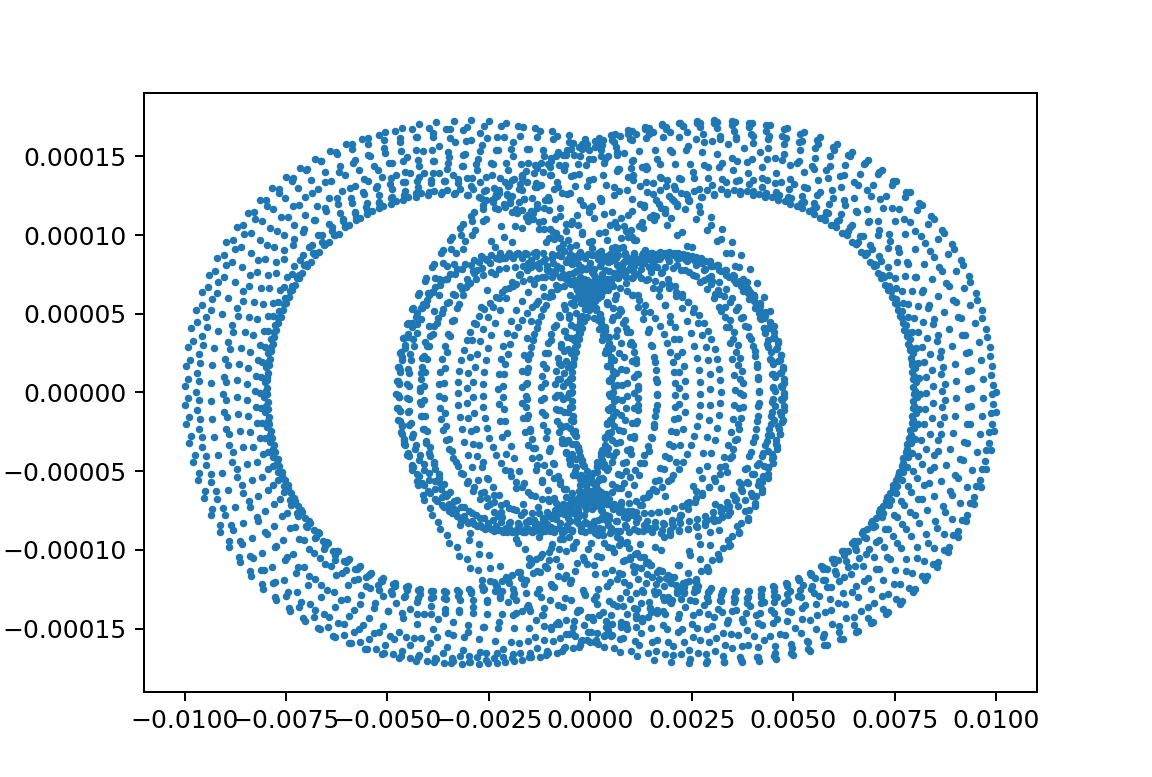
m_2が小さくなると横釣り鐘型
xp1_L150000L249999m110000m21000y010.05
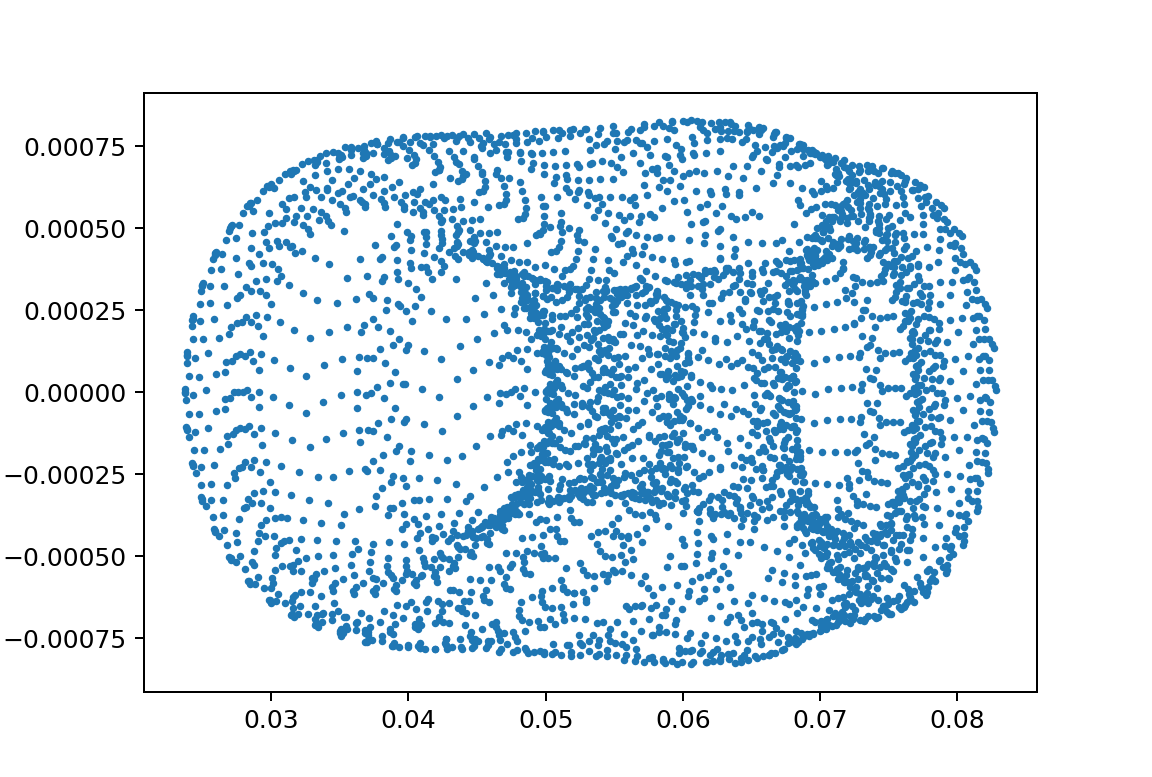
xp1_L150000L250000m110000m21000y010.08
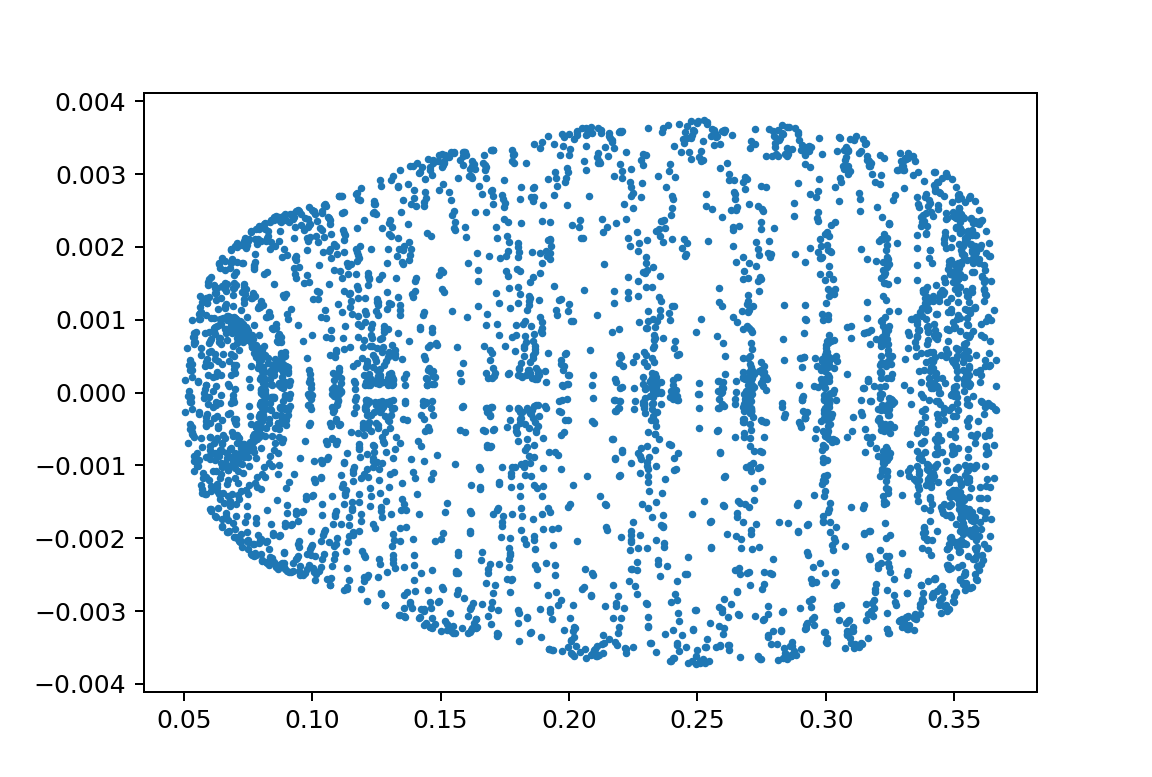
もう一つ
xp1_L150000L249900m110.0m21.75y010.05001
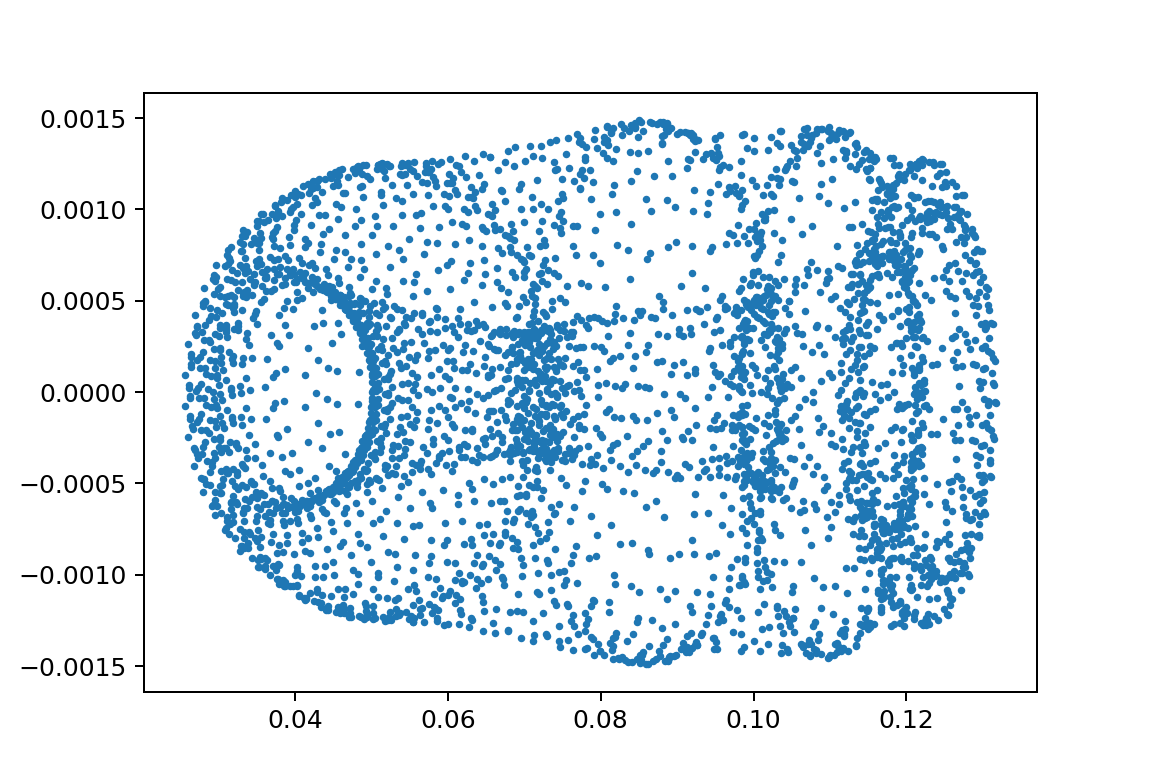
xp1_L150000L249900m110.0m21.75y010.0501
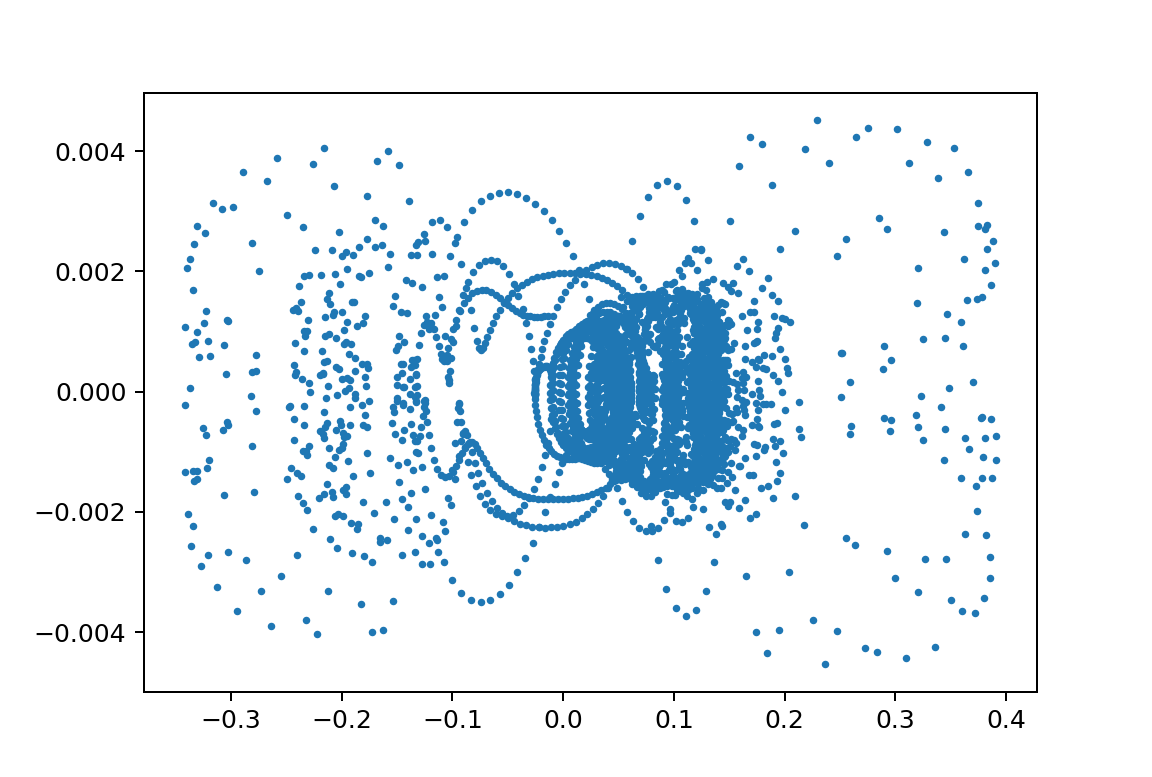
xp1_L150000L249900m110.0m21.75y010.0502
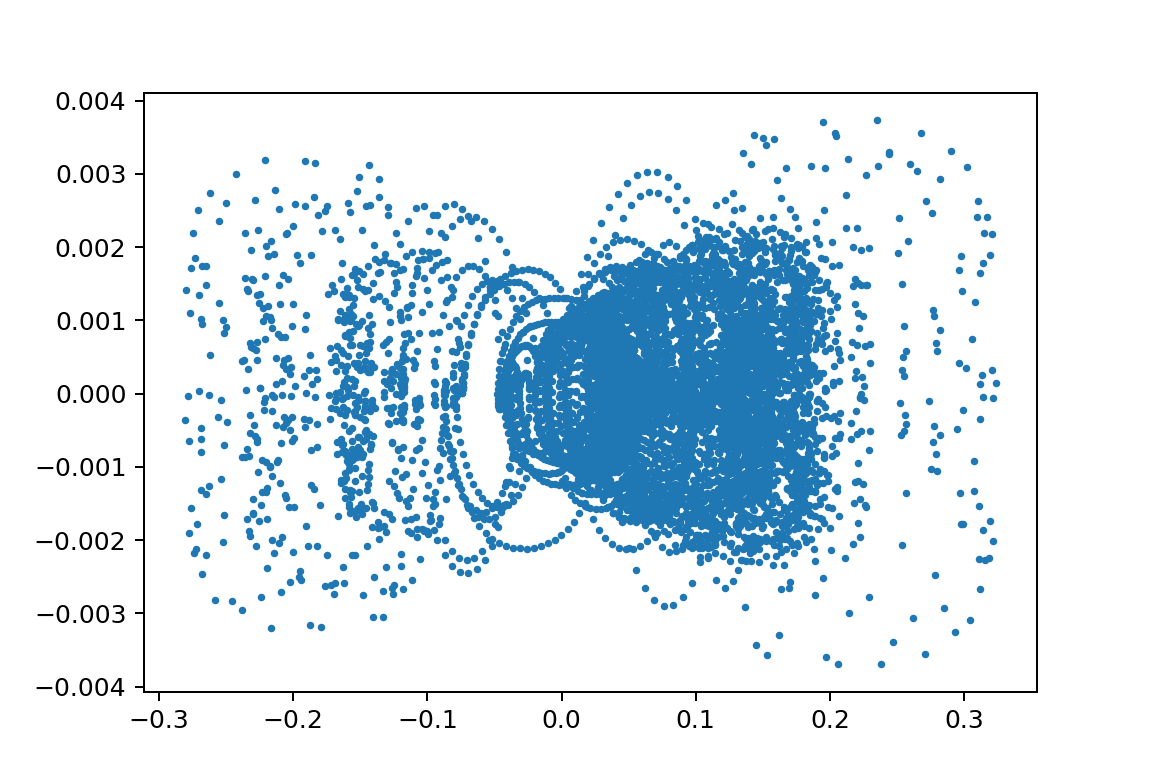
xp1_L150000L249900m110.0m21.75y010.0503
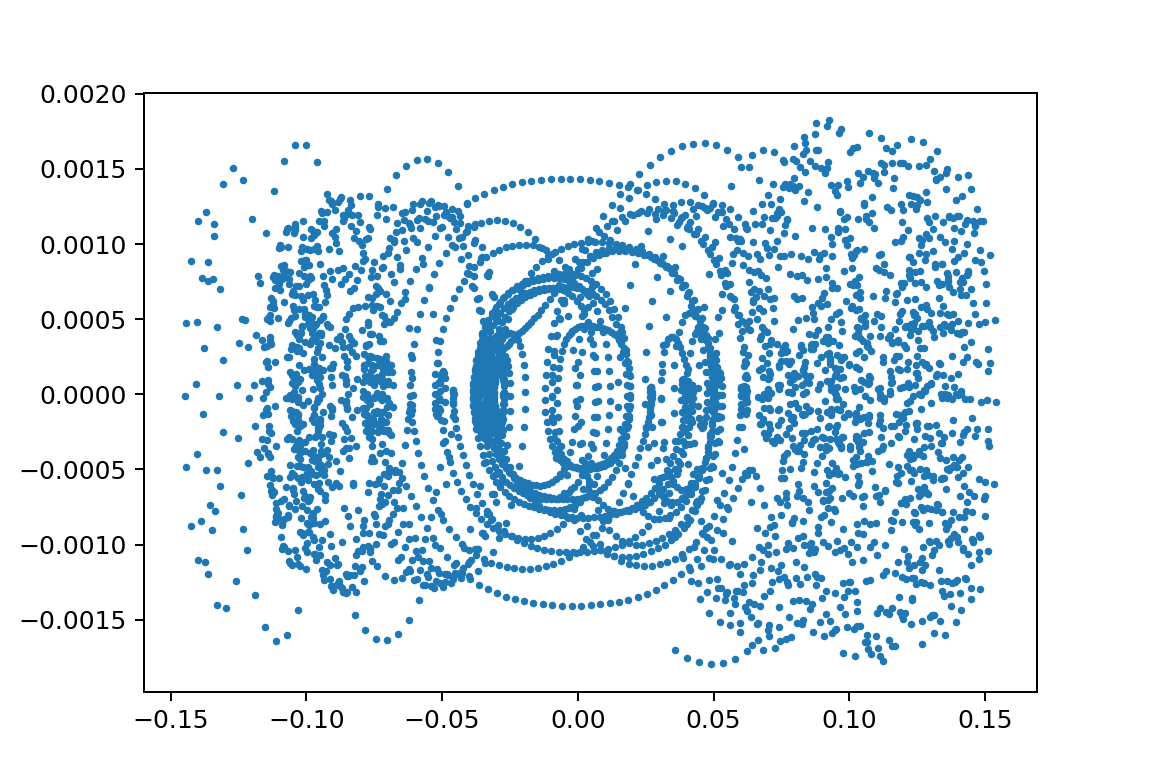
xp1_L150000L249900m110.0m21.75y010.0504
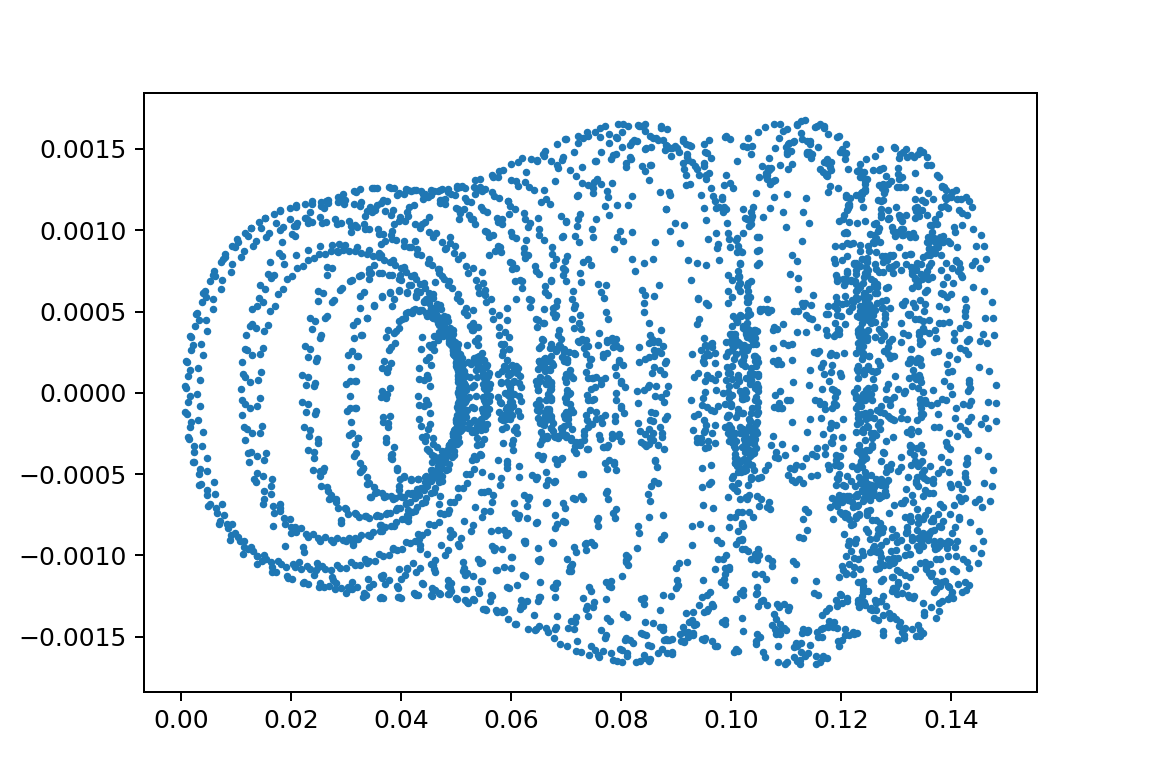
xp1_L150000L249900m110.0m21.75y010.051
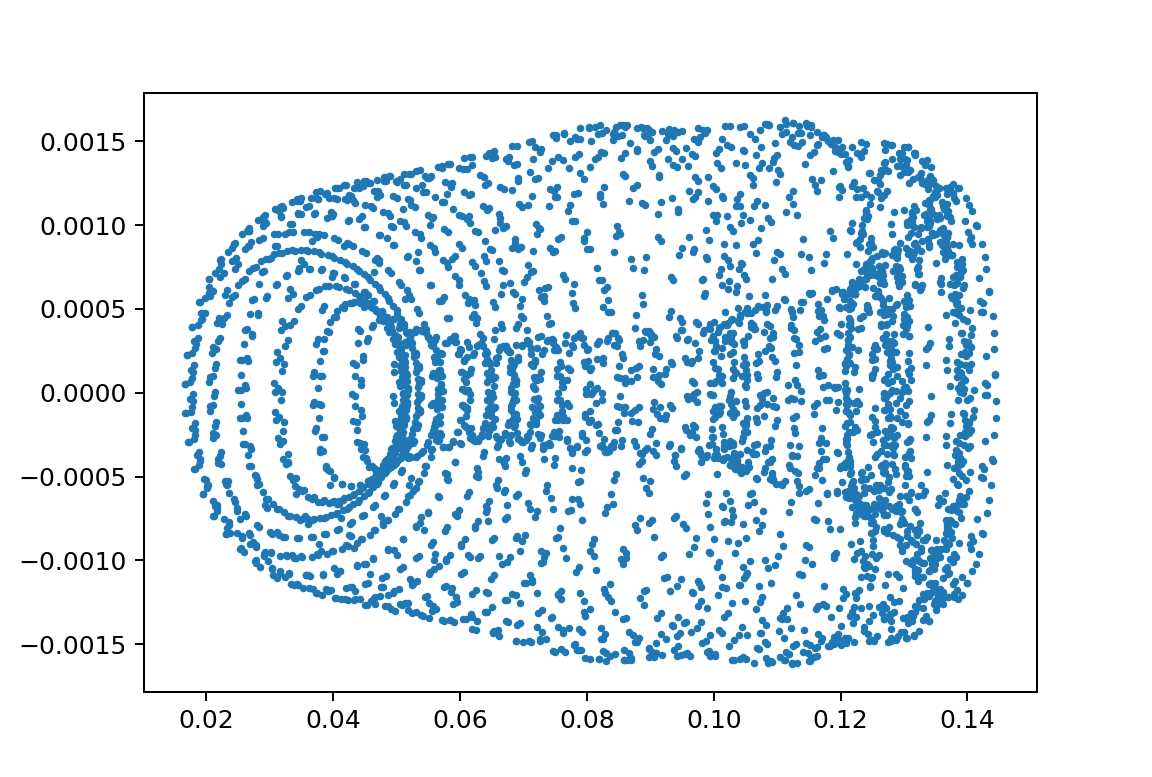
そして
xp2_L0.992M0.019600000000000003omegaJ0.14893617021276595y010.4
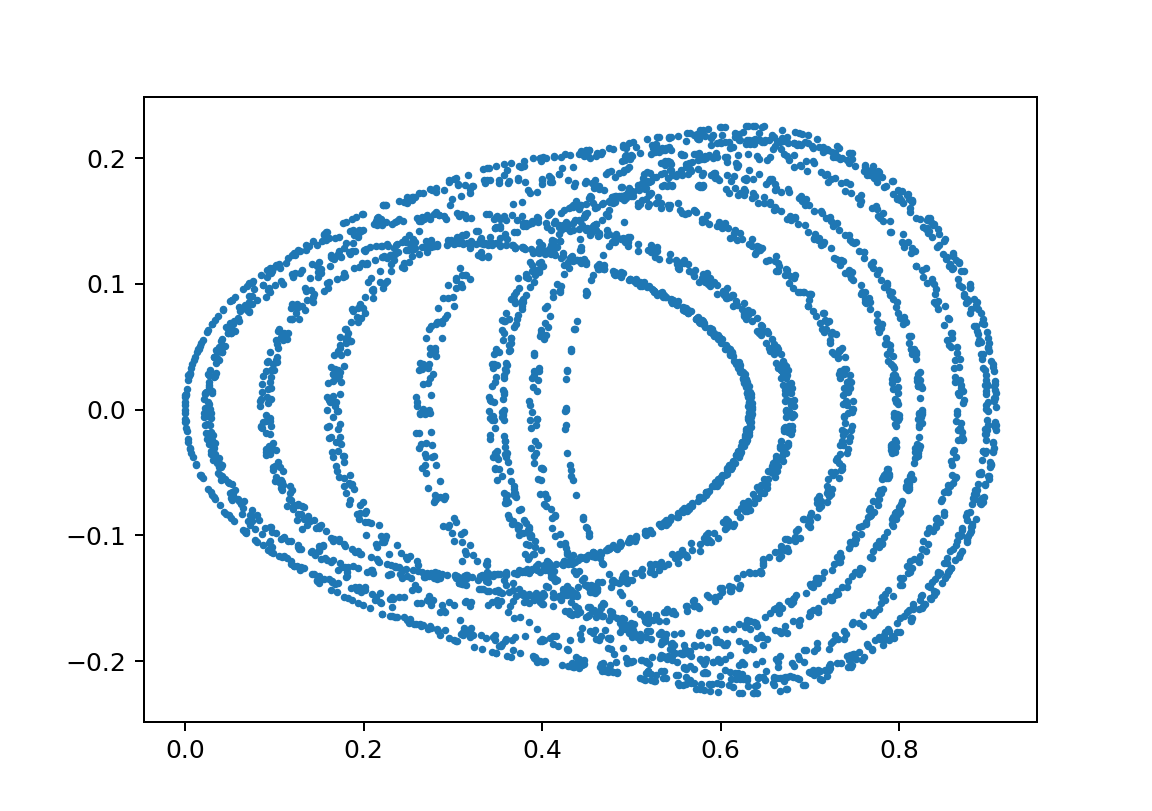
xp2_L0.99M0.019600000000000003omegaJ0.14893617021276595y010.40001
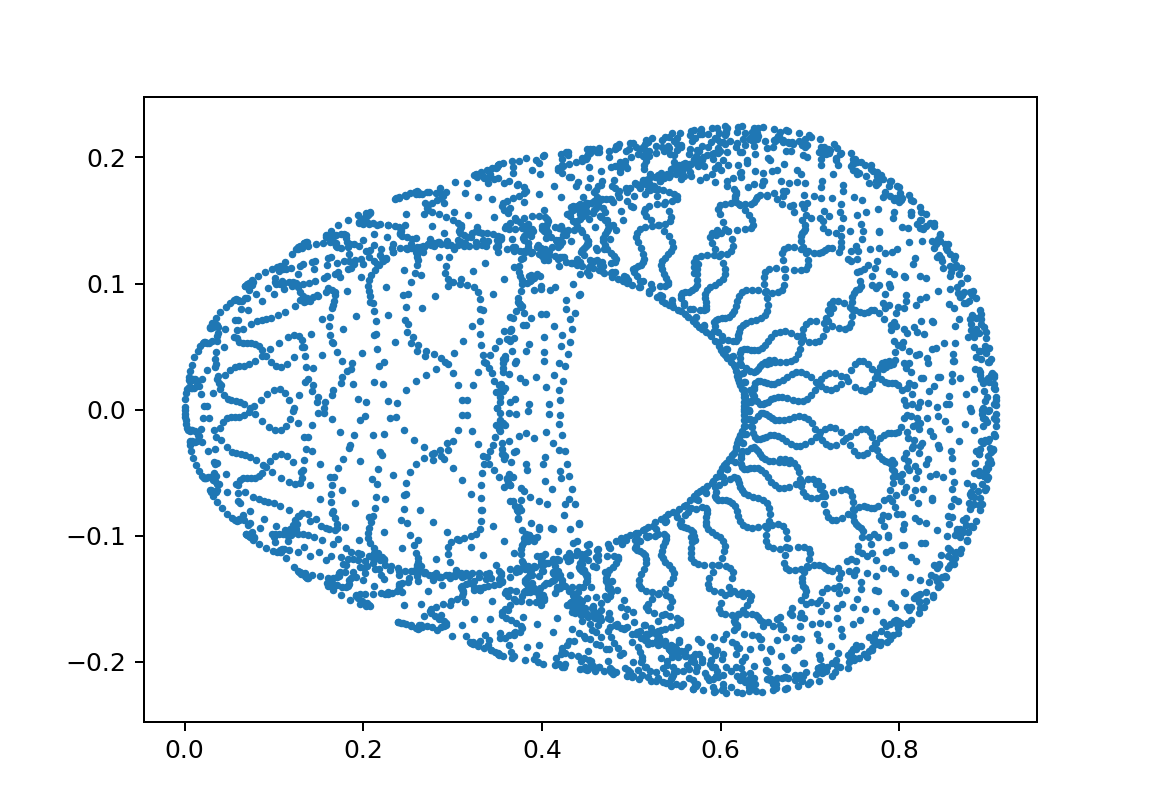
xp2_L0.99M0.019600000000000003omegaJ0.14893617021276595y010.400001
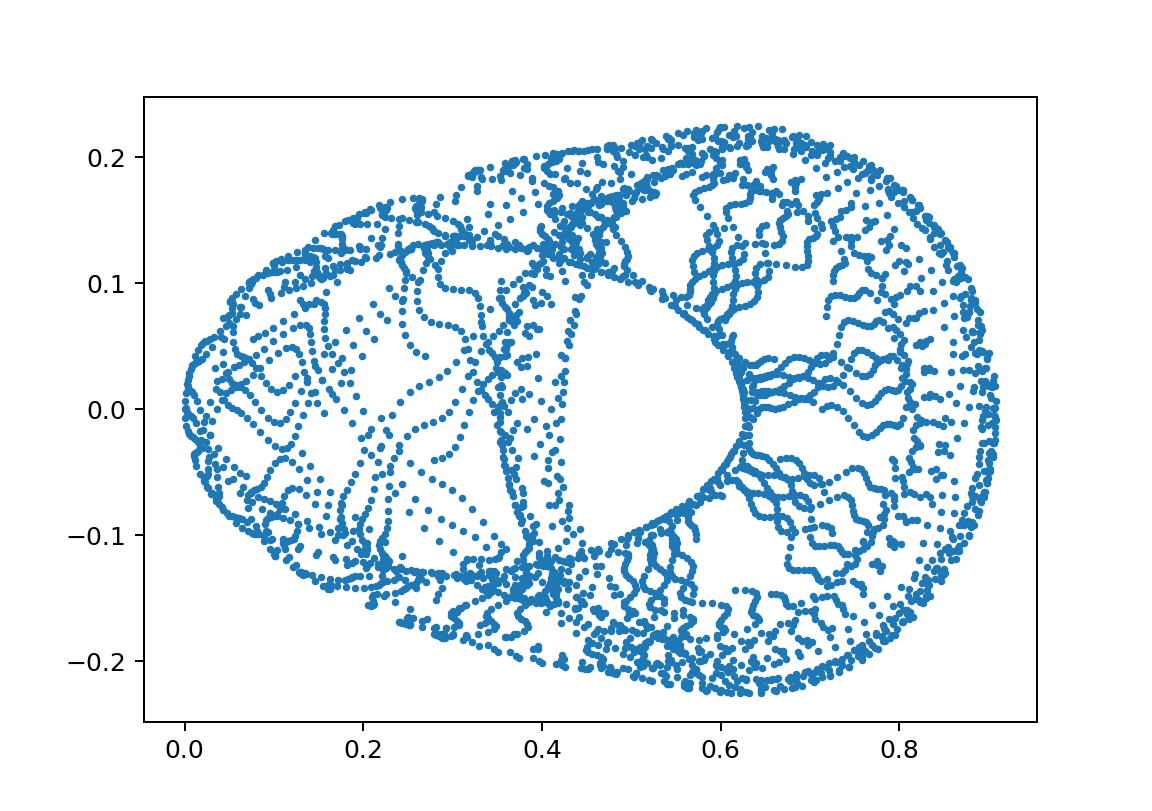
xp2_L0.99M0.019600000000000003omegaJ0.14893617021276595y010.400005
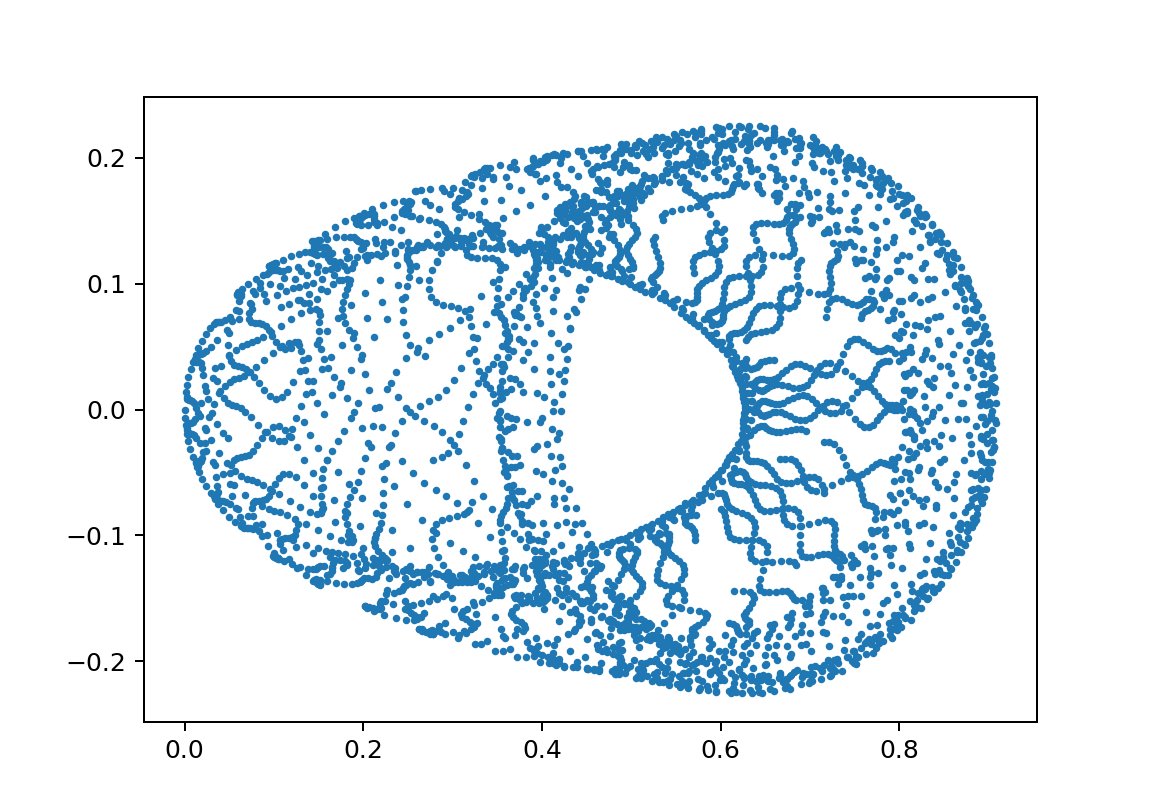
xp2_L0.988M0.019600000000000003omegaJ0.14893617021276595y010.4
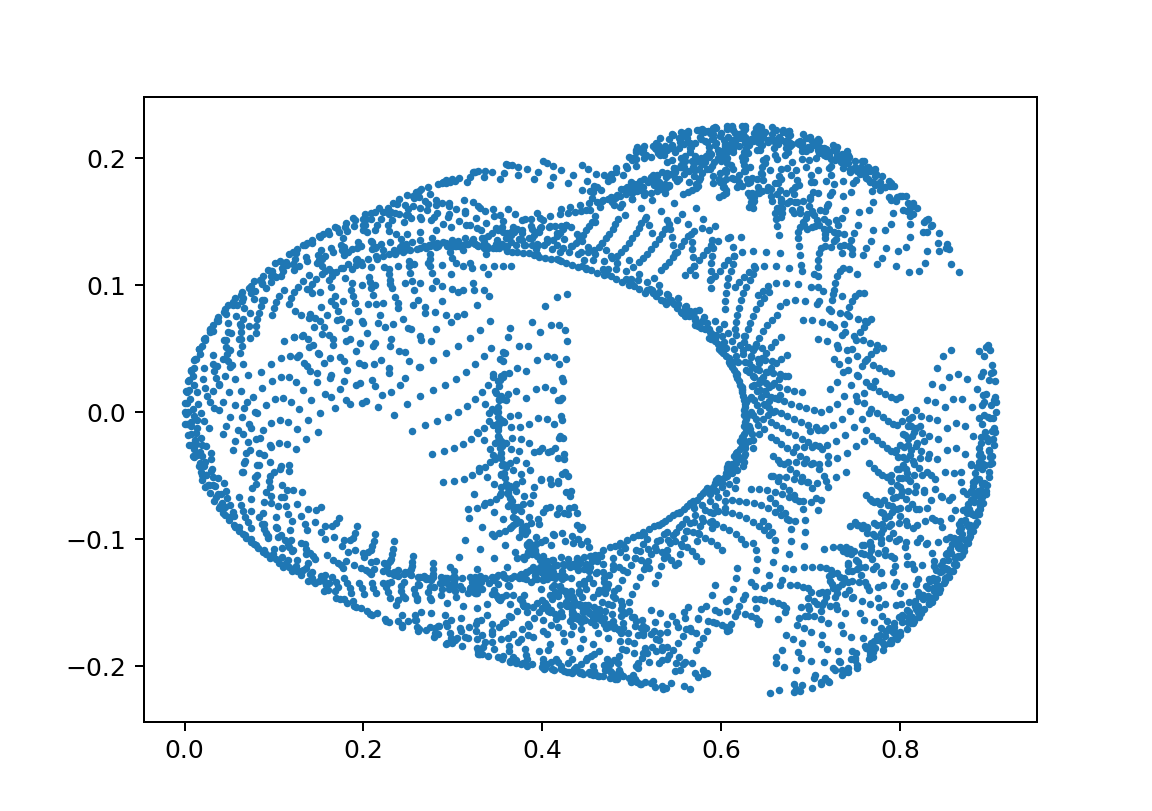
まとめ
・単振り子連結の二重振り子の微分方程式の数値解析でカオスを見た
・カオスアートはある程度コントロール可能である
・カオス領域では、環境鋭敏性があるので実は剛体振り子として扱わないといけない
・棒連結二重振り子はより剛体振り子として振舞うことが予想される
・まずは通常の質点としての棒連結振り子の振舞を見る予定