今回は単振り子連結二重振り子のシミュレーションをやってみた。
参考に挙げたようにそれなりに情報があっていまさら感もあるが、やはりなんとなくすっきりしないので、もう少し深堀しようと思う。
※アトラクターの例示はあっても位相空間での振舞がなんとなく見せ切れていないという焦燥
【参考】
①Processingで二重振り子(Double Pendulum)の軌跡を描く
②二重振り子@Wikipedia
③my physics lab logo Double Pendulum
④二重振り子@カオス&非線形力学入門
やったこと
(1)やはり二重振り子の紋章
(2)関数のコード
(3)運動方程式の一考察
(1)やはり二重振り子の紋章
今回のモデルは、参考①の微分方程式の解が中心です。この方程式の出典は参考③にありますが、最後のところの導出が必要で、ウワンはこれは導出していませんのであしからず。
※参考④の方が見通しがよく、おまけで記載しましたが棒連結の話と合わせて次回の記事で今回の解を検証する予定です
ということで、今回は以下のモデルを用いて、計算した二重振り子の紋章の結果を示します。
\theta_1'' = \frac{-g(2m_1 + m_2){\sin \theta_1} - m_2g{\sin (\theta_1 - 2\theta_2) -2{\sin (\theta_1 - \theta_2)}}m_2(\theta_2'^2L_2+\theta_1'^2L_1{\cos(\theta_1 - \theta_2))}}{L_1(2m_1+m_2-m_2{\cos(2\theta_1 - 2\theta_2))}}
\theta_2'' = \frac{2{\sin (\theta_1 - \theta_2)(\theta_1'^2L_1(m_1+m_2)+g(m_1+m_2){\cos \theta_1}}+\theta_2'^2L_2m_2{\cos(\theta_1 - \theta_2))}}{L_2(2m_1+m_2-m_2{\cos(2\theta_1 - 2\theta_2))}}
今回もとても魅力的な紋章(位相空間での振舞)が得れました。
いろいろな紋章
xp1;L11L21m1100m21y010.01
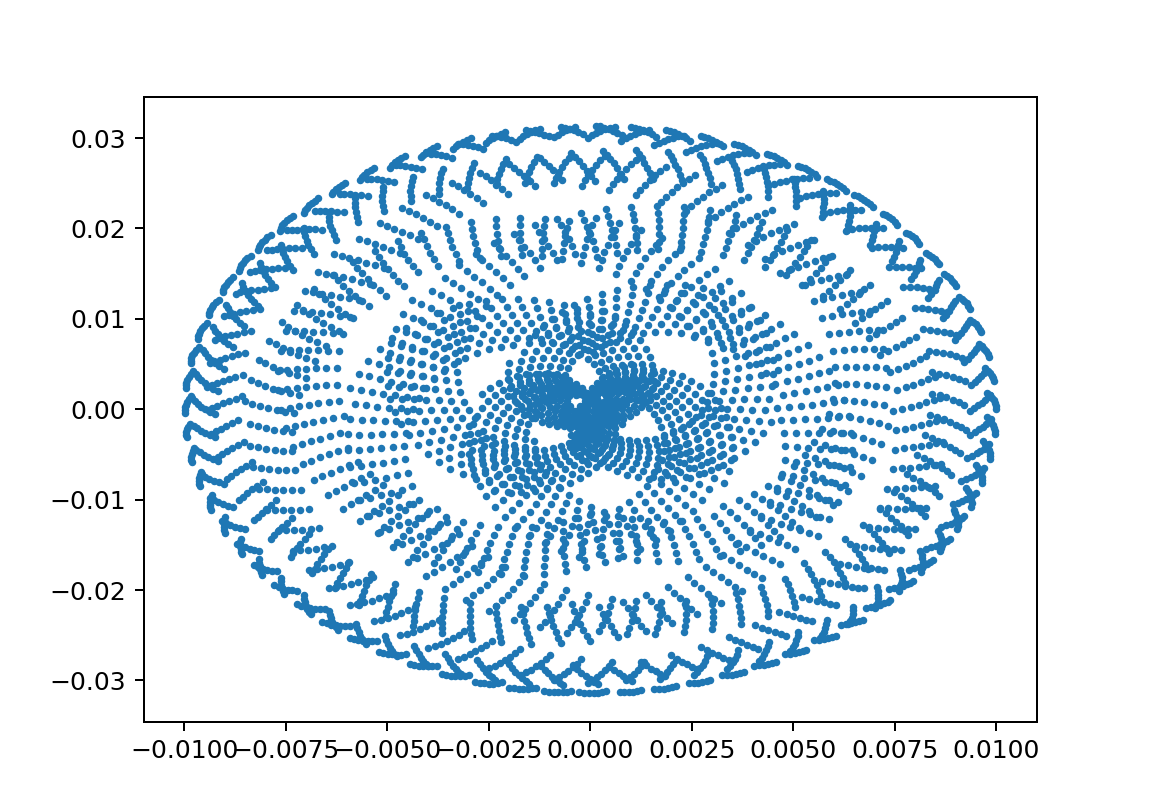
xp1;L11L21m1100m21y010.001
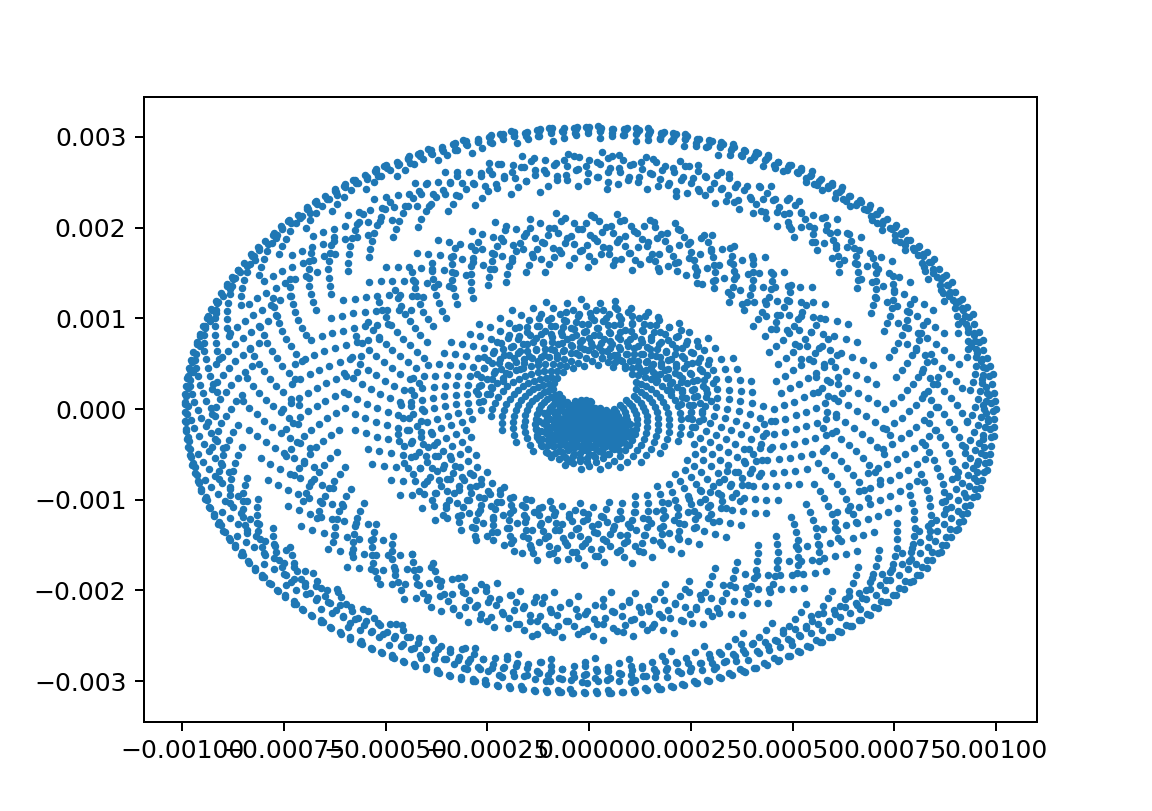
xp1L11L21m110m21y010.5
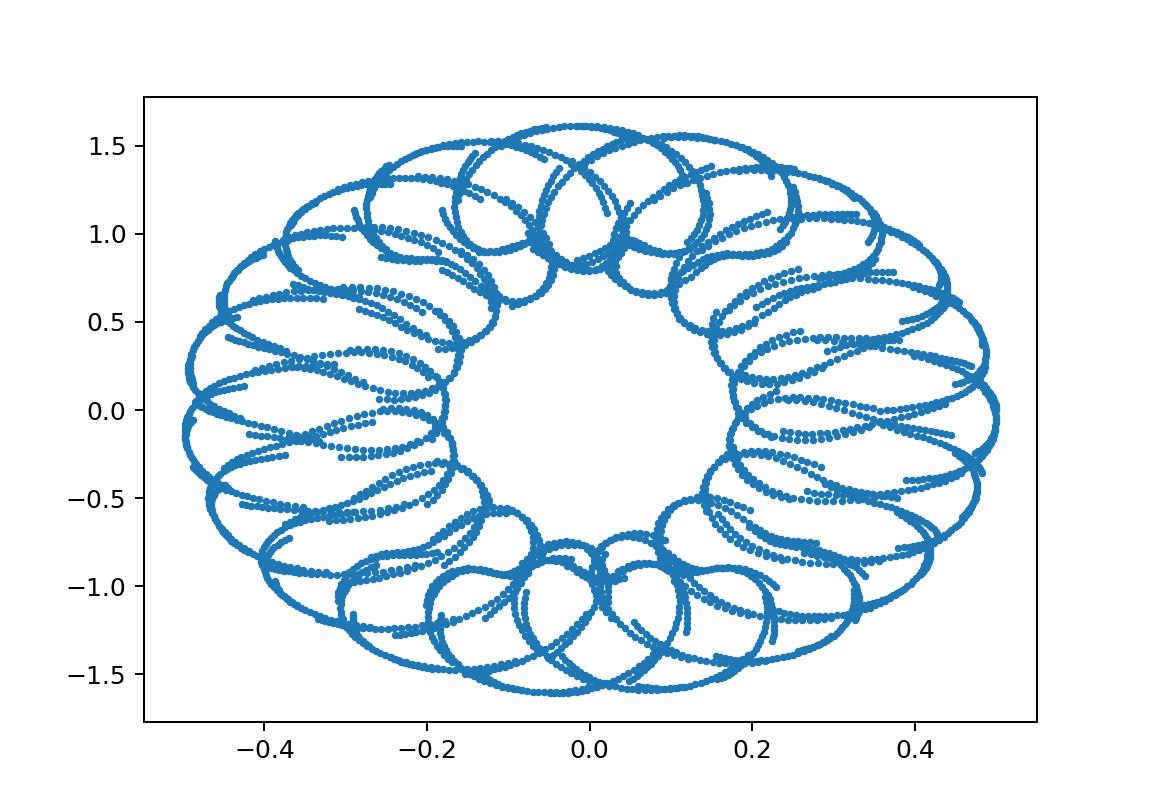
xp1L11L21m1100m21y010.1
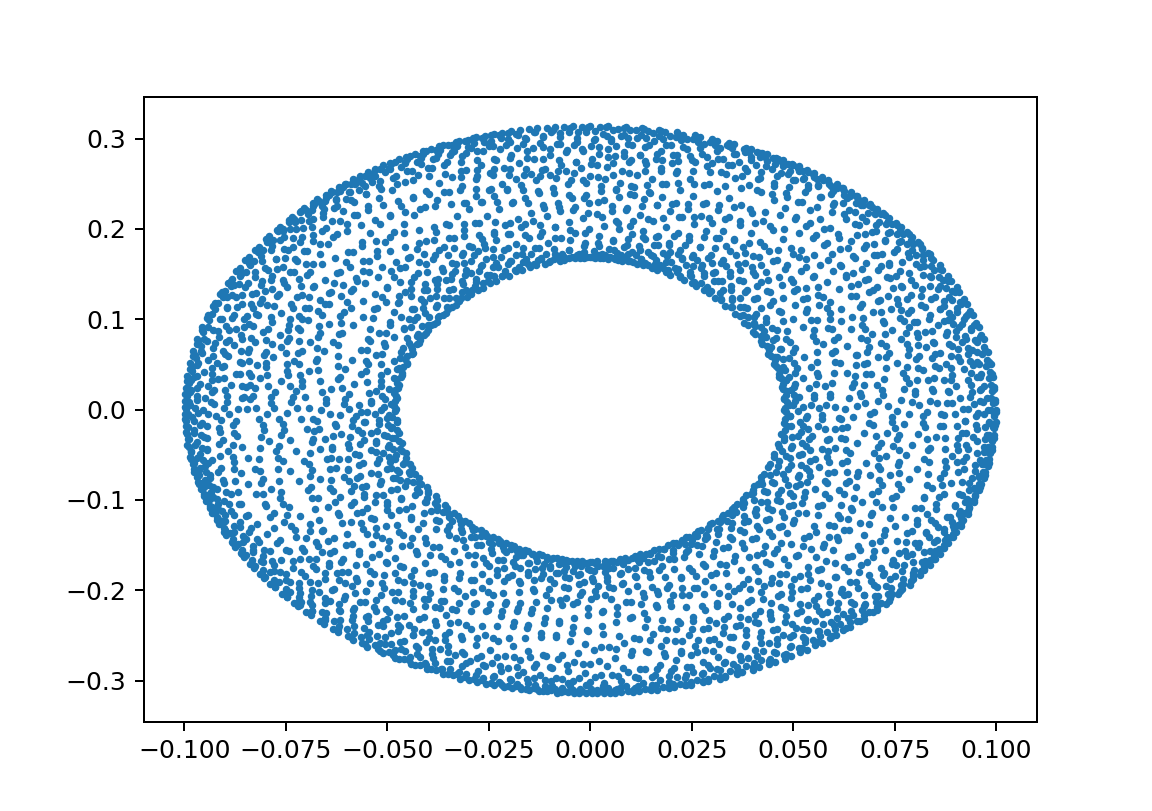
xp1L110L25m11m21y010.5
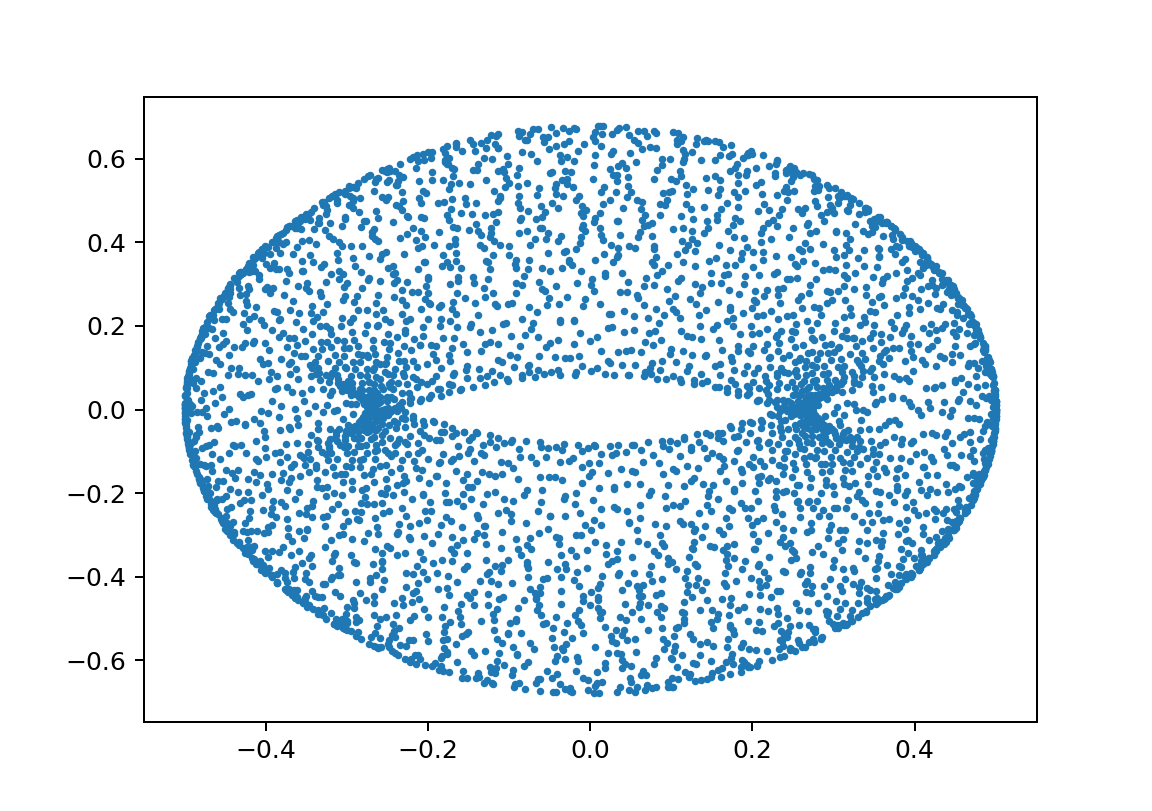
xp1L11L21m11m21y010.5
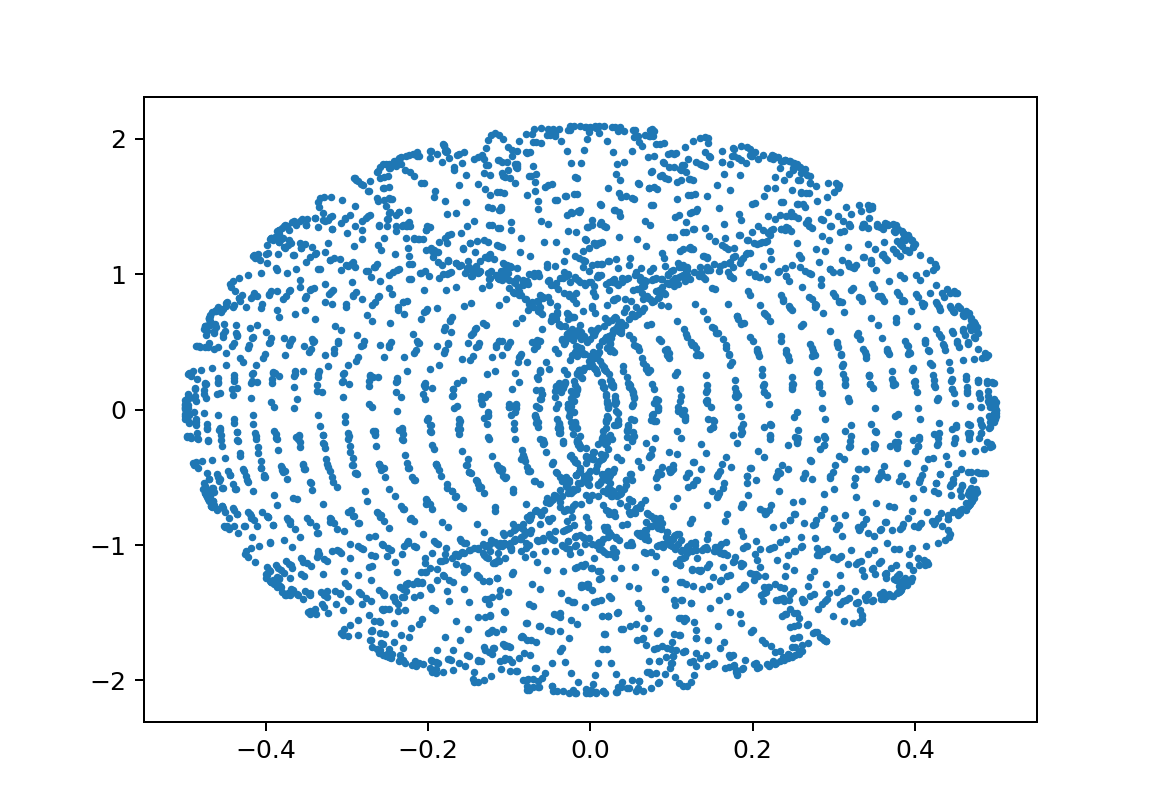
xp1L110000L220000m110m2100y010.5
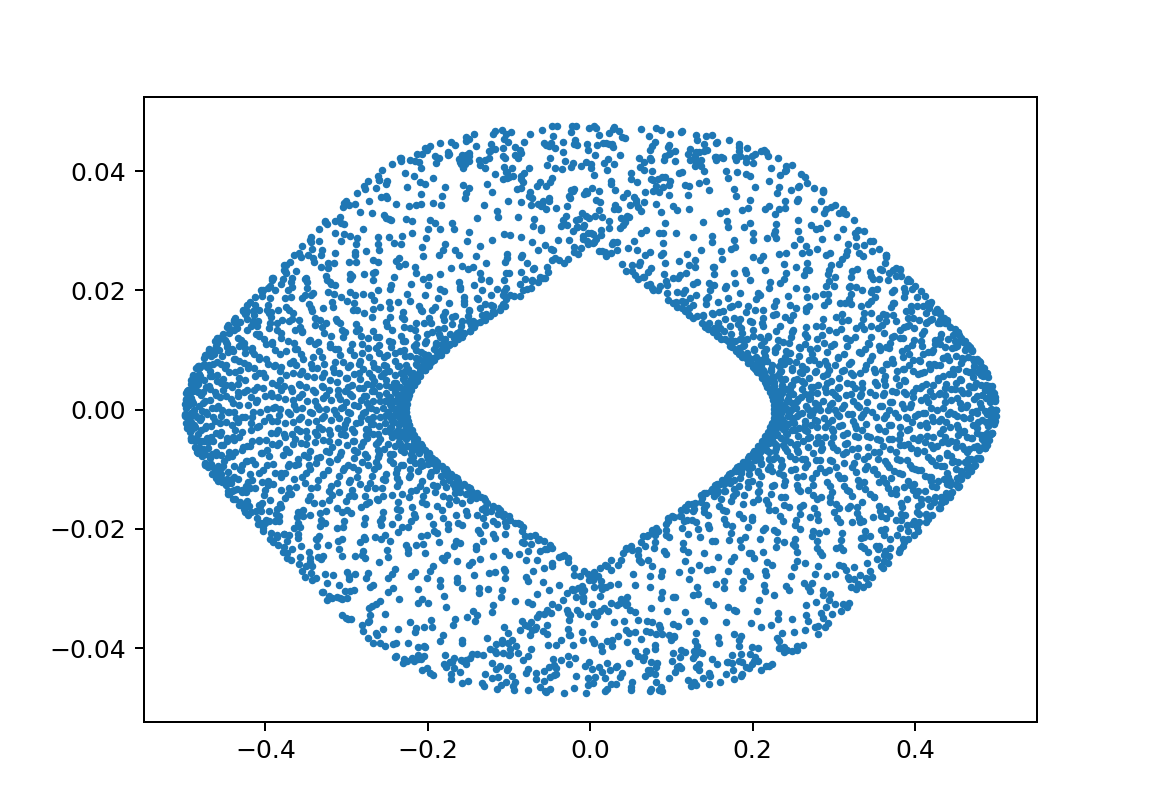
xp1;L1500000L250000m11000m21000y010.5
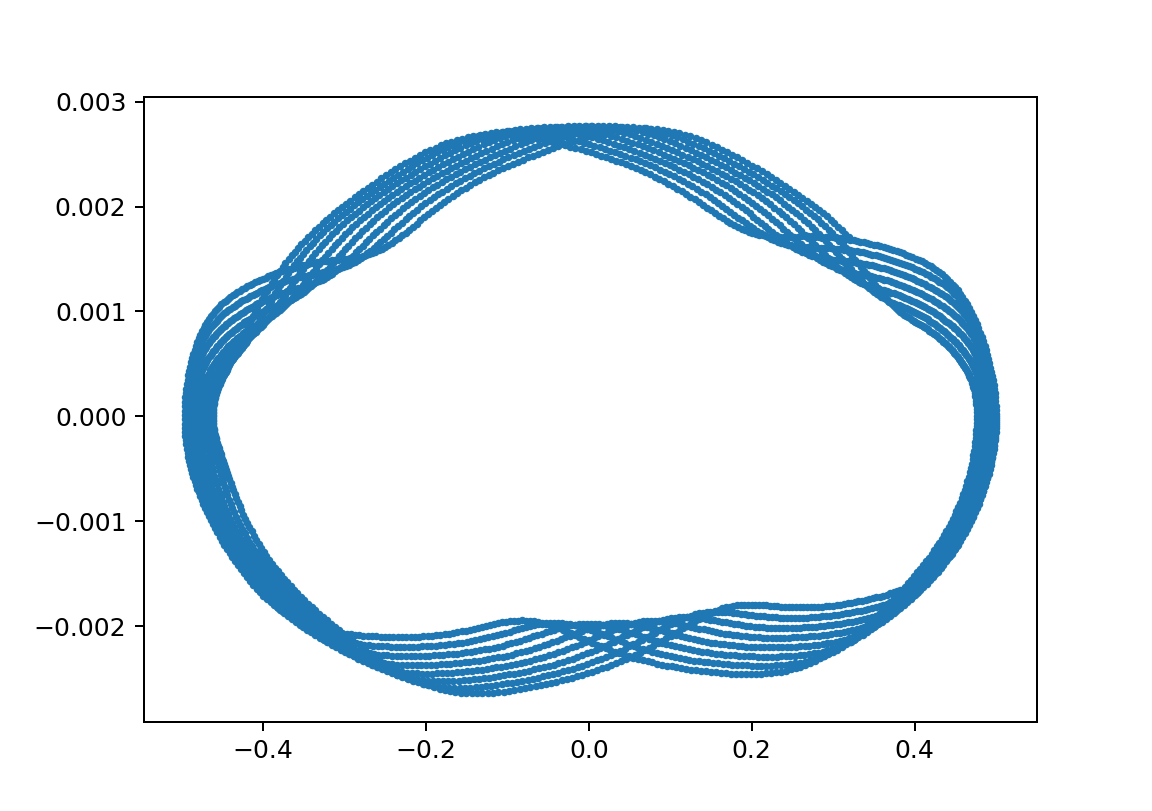
xp2;L11L21m11m21y010.5
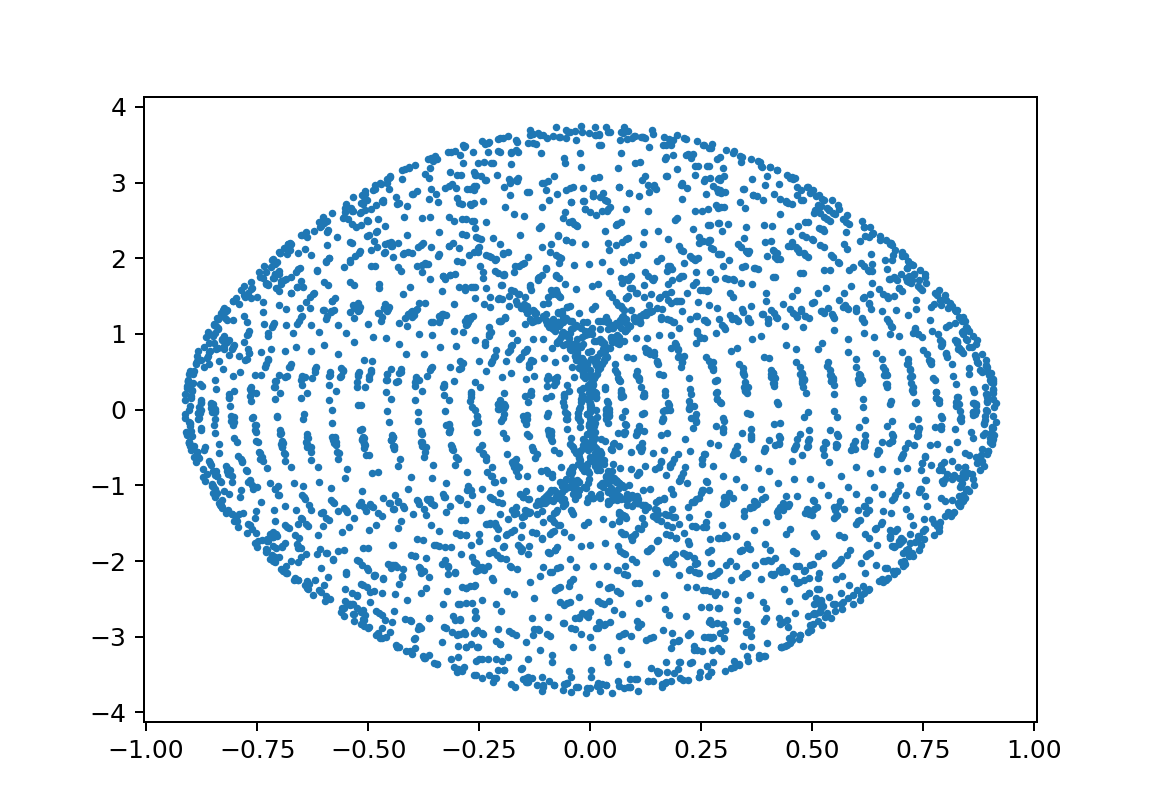
xp1;L11000000L2500000m11000m21000y010.5
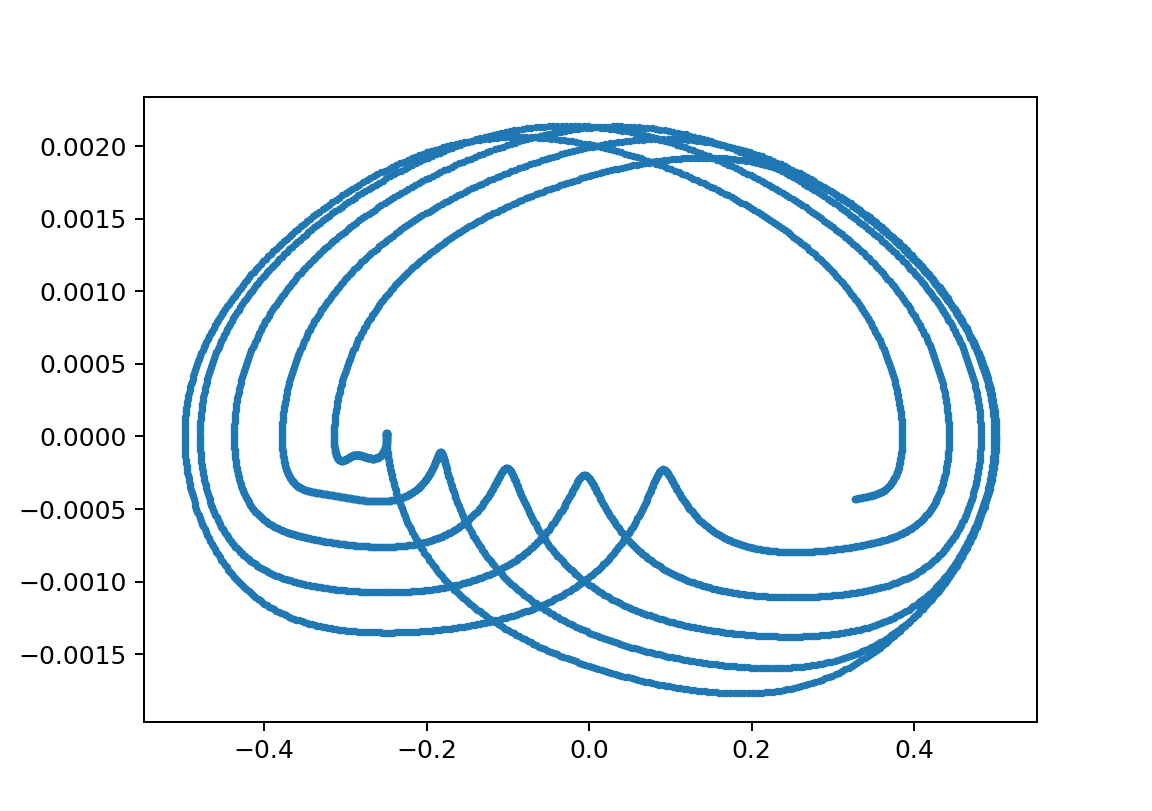
初期値鋭敏性
xp1の鋭敏性
xp1_L150000L247000m110000m21750y011.0
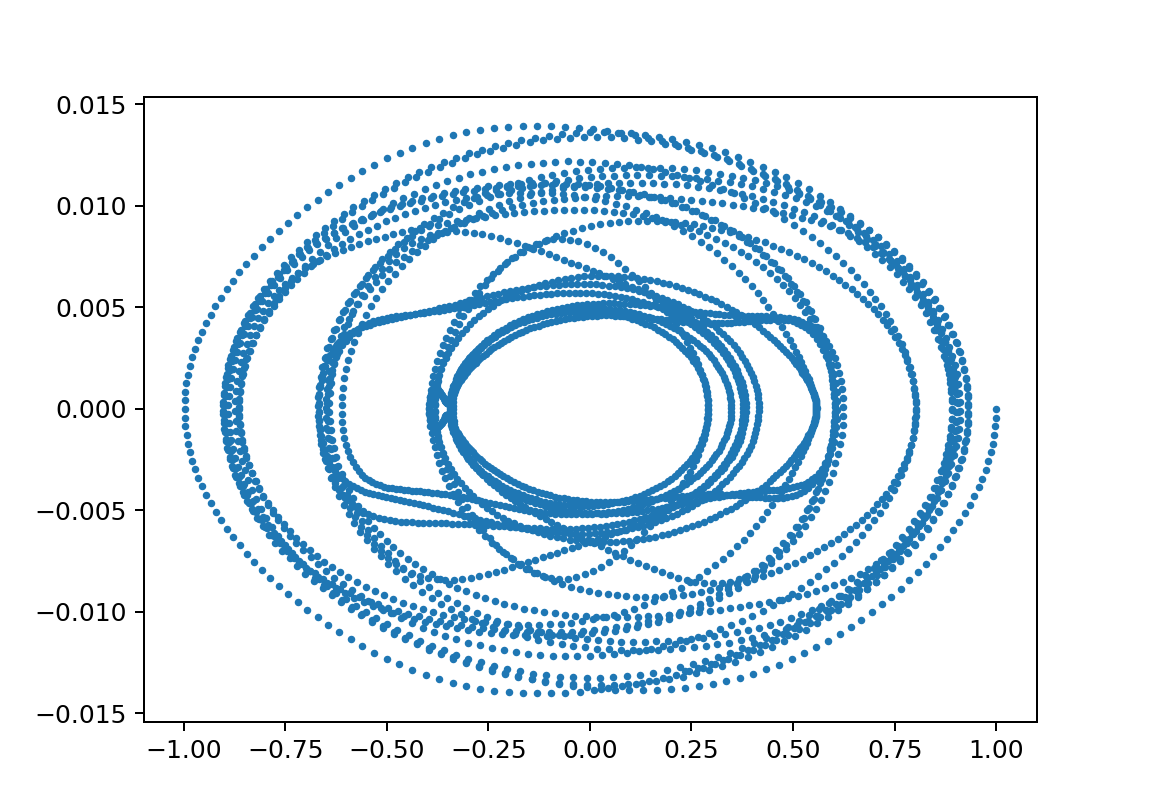
xp1_L150000L247000m110000m21750y011.001
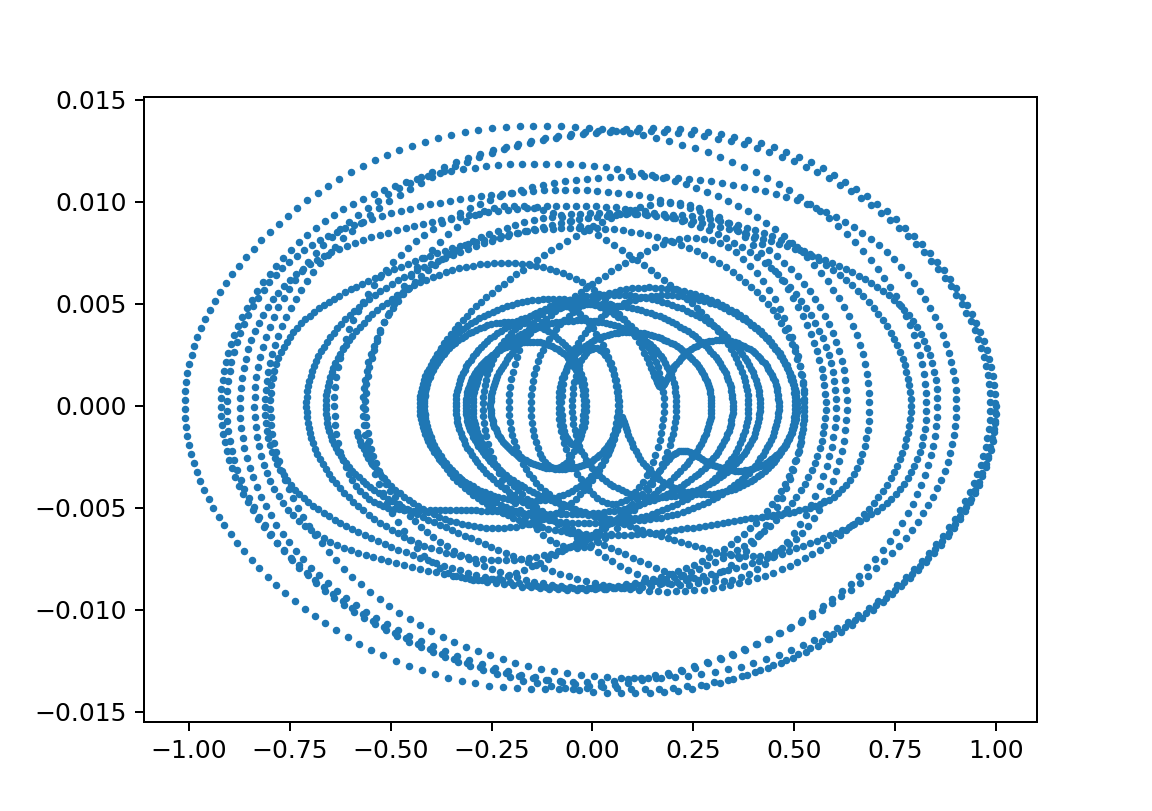
xp1_L150000L247000m110000m21750y011.002
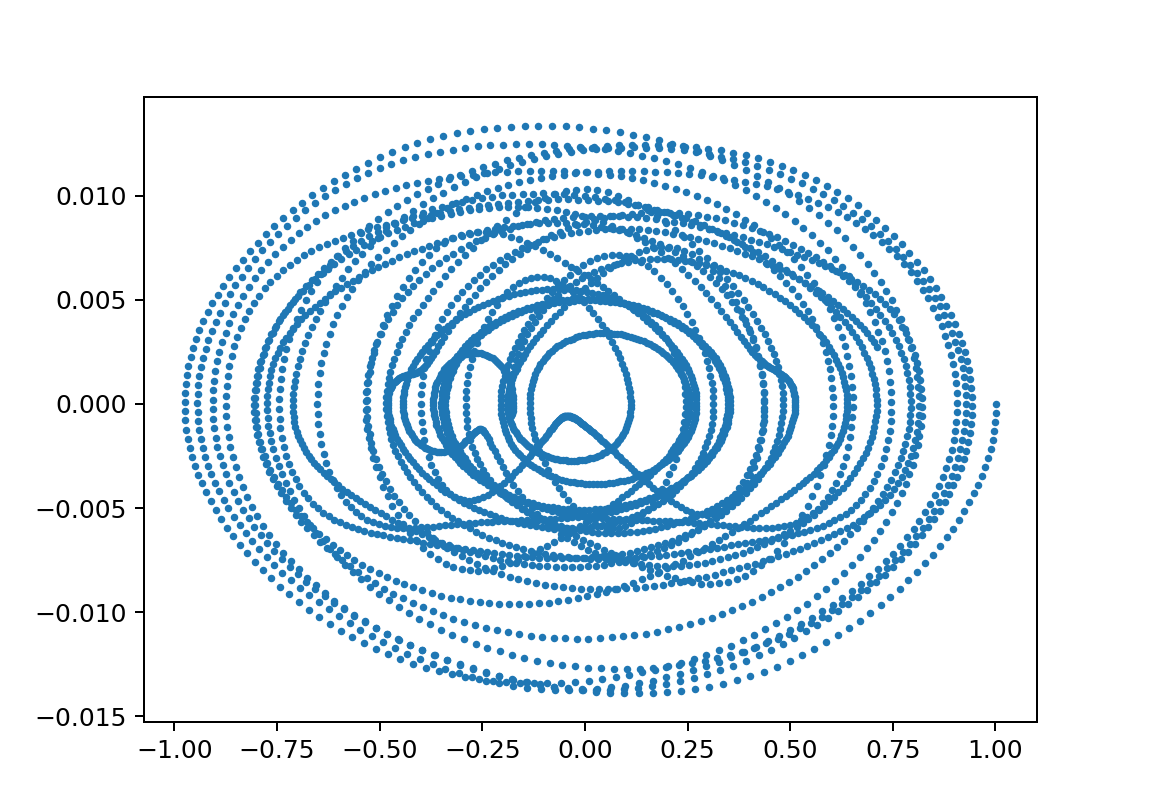
xp1_L150000L247000m110000m21750y011.003
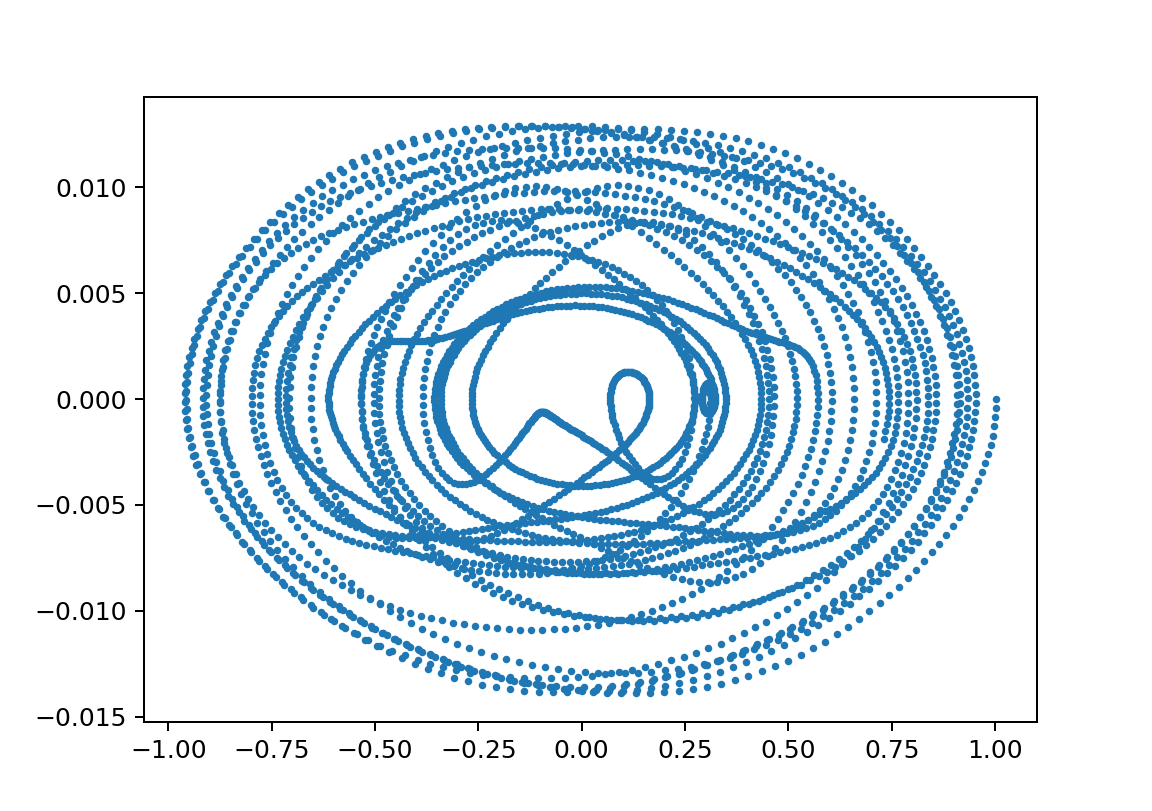
xp2の鋭敏性;L1;5000L2;4700m1;10000m2;1750
xp2_L15000L24700m110000m21750y011.0
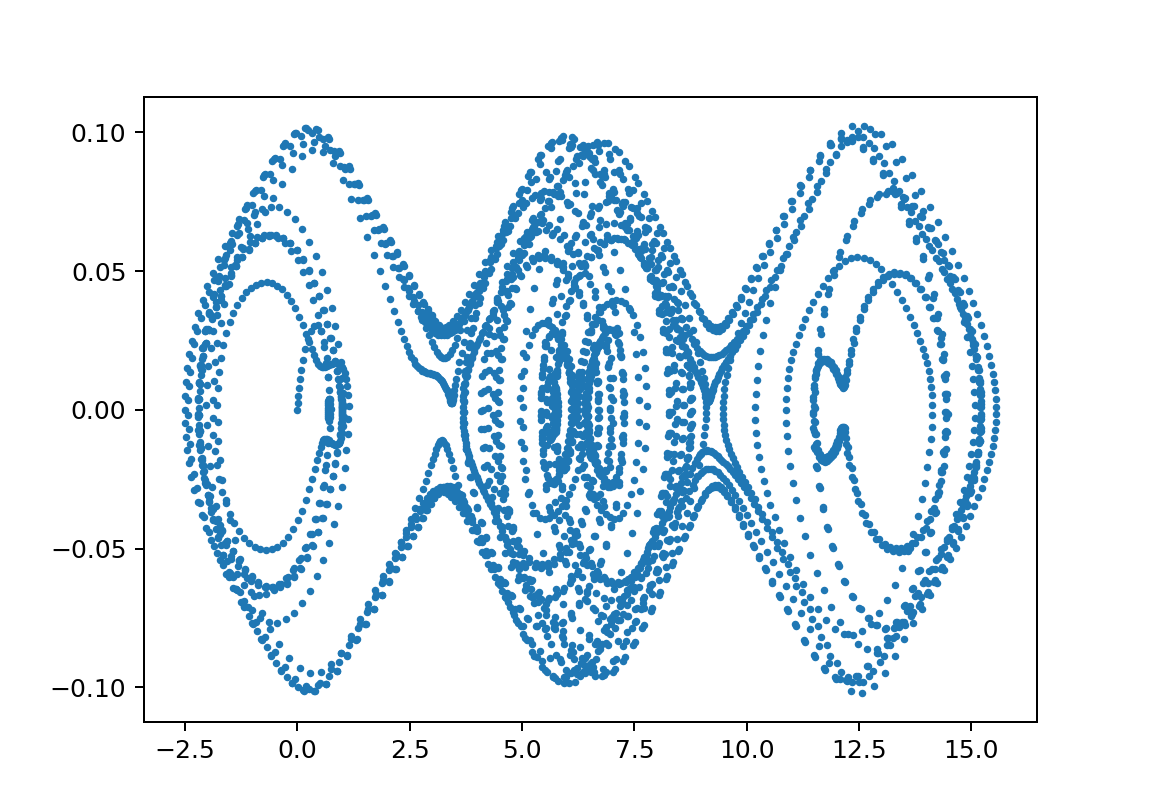
xp2_L15000L24700m110000m21750y011.001
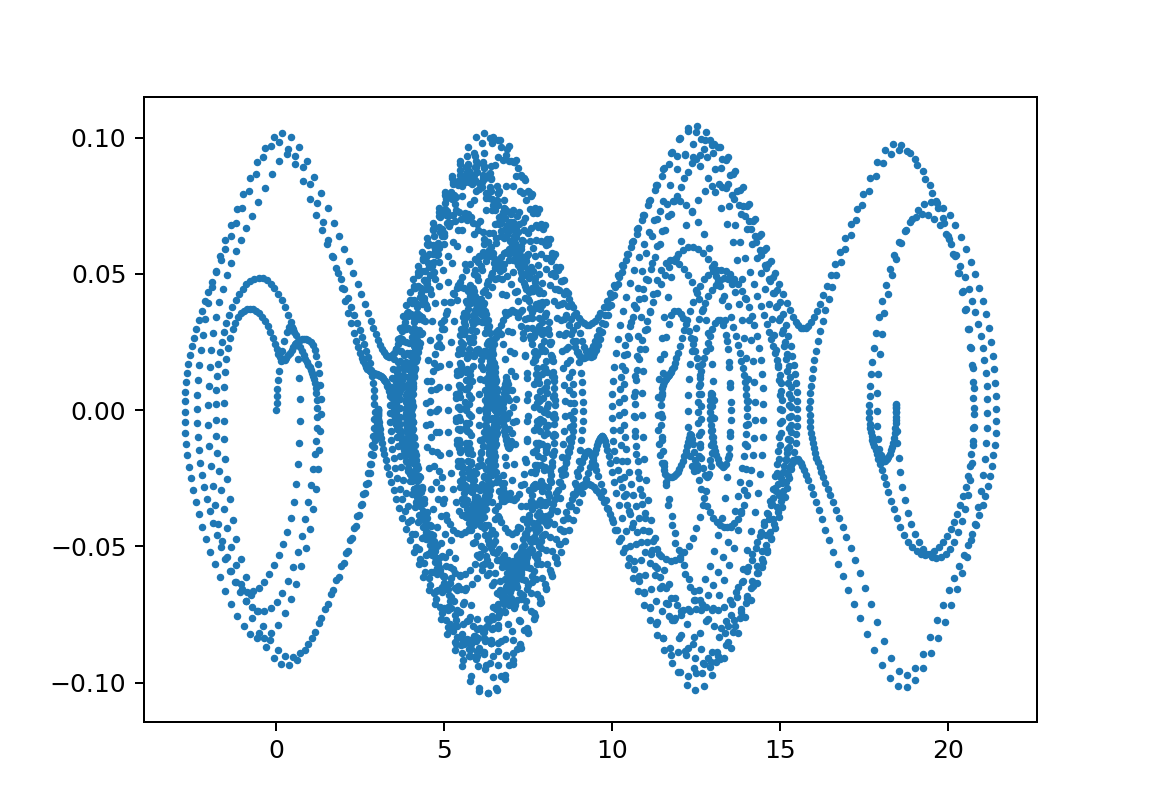
xp2_L15000L24700m110000m21750y011.002
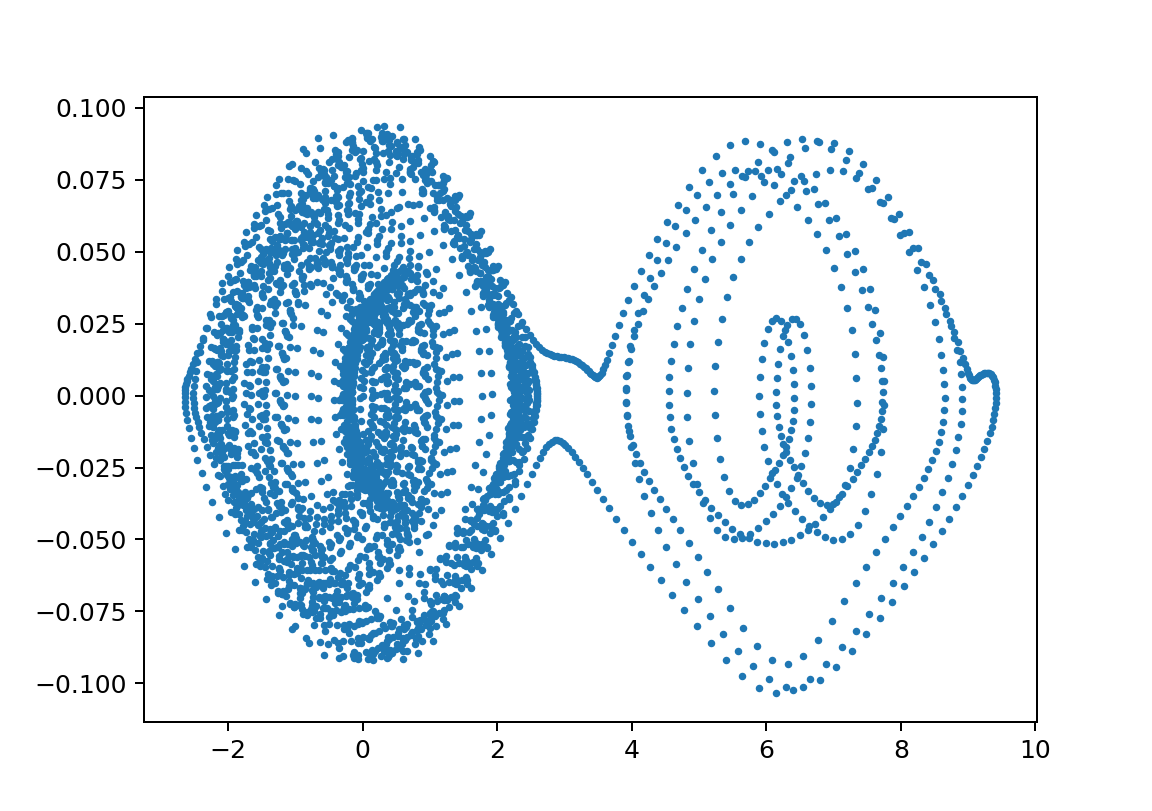
xp2_L15000L24700m110000m21750y011.003
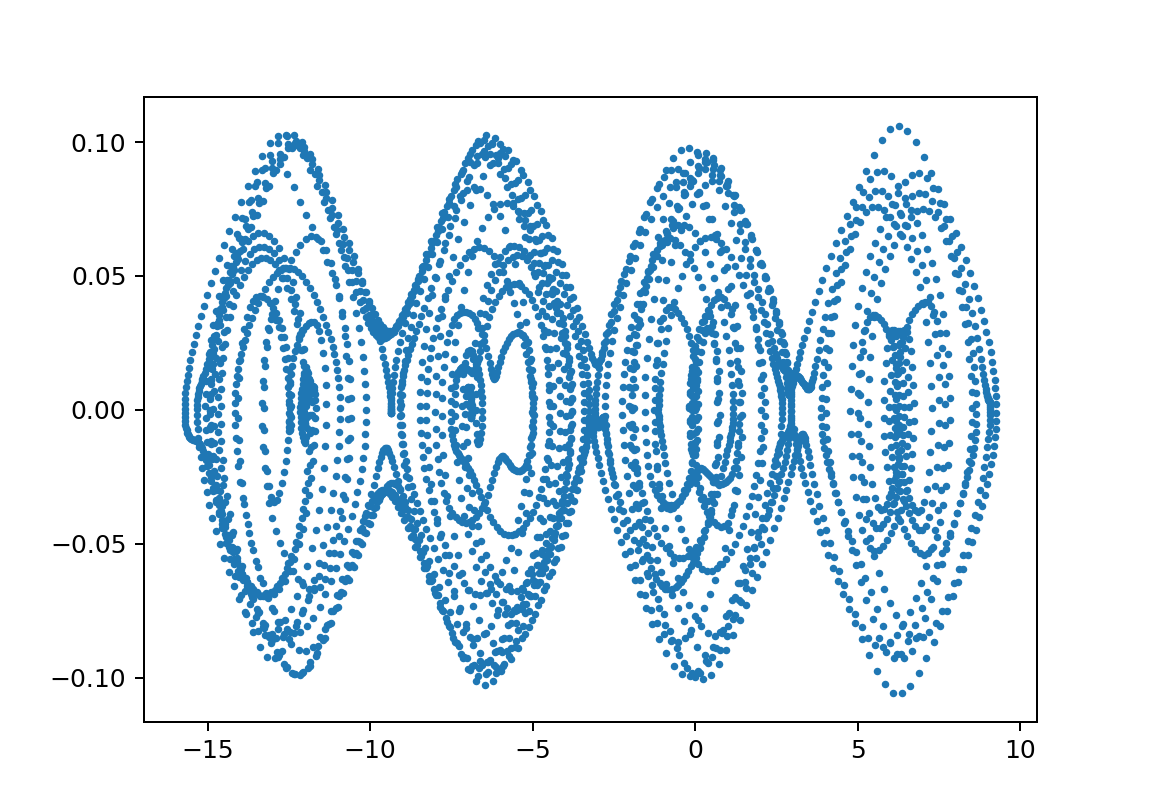
xp2の鋭敏性;L1;500L2;450m1;10000m2;1750
xp2_L1500L2450m110000m21750y011.0
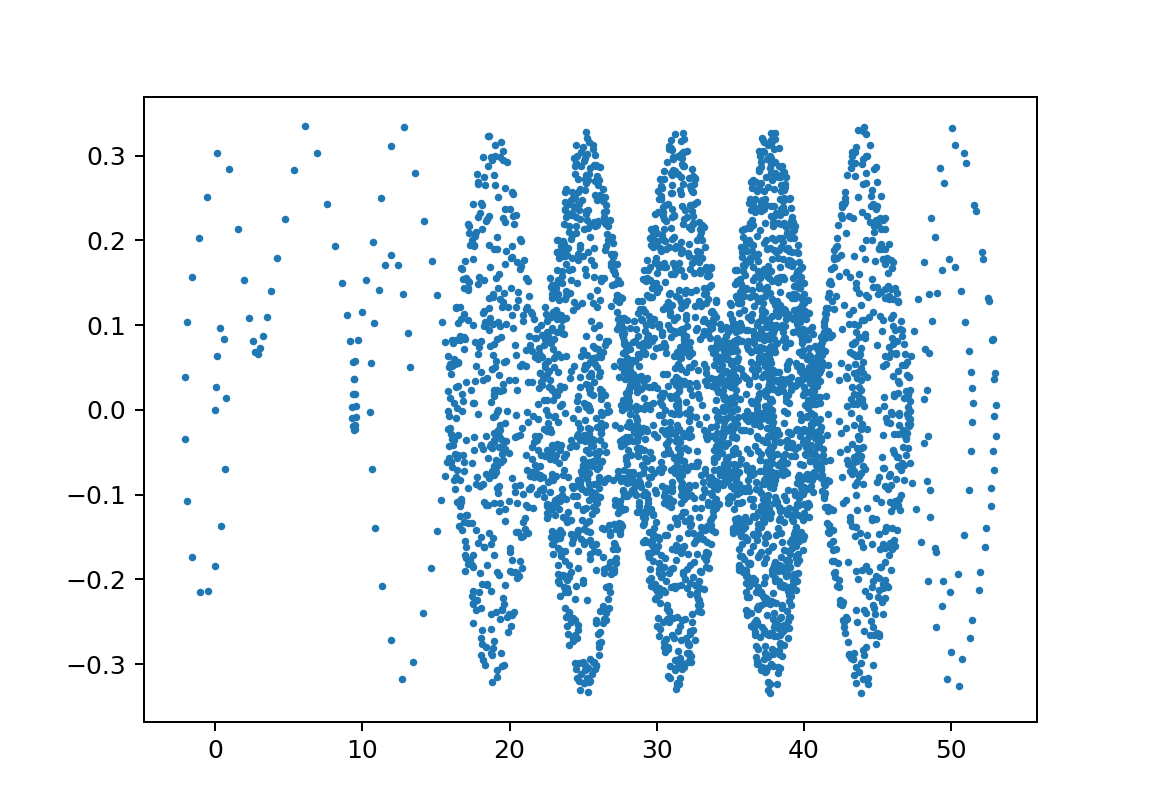
xp2_L1500L2450m110000m21750y011.001
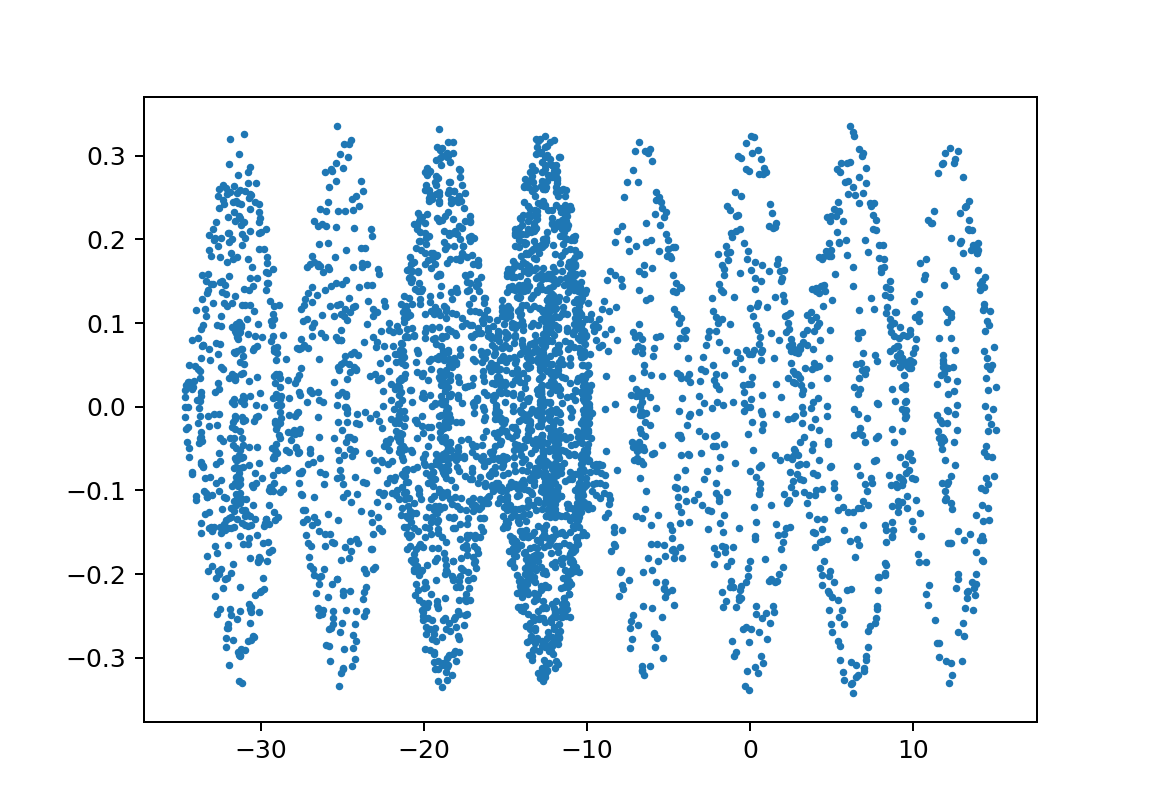
xp2_L1500L2450m110000m21750y011.002
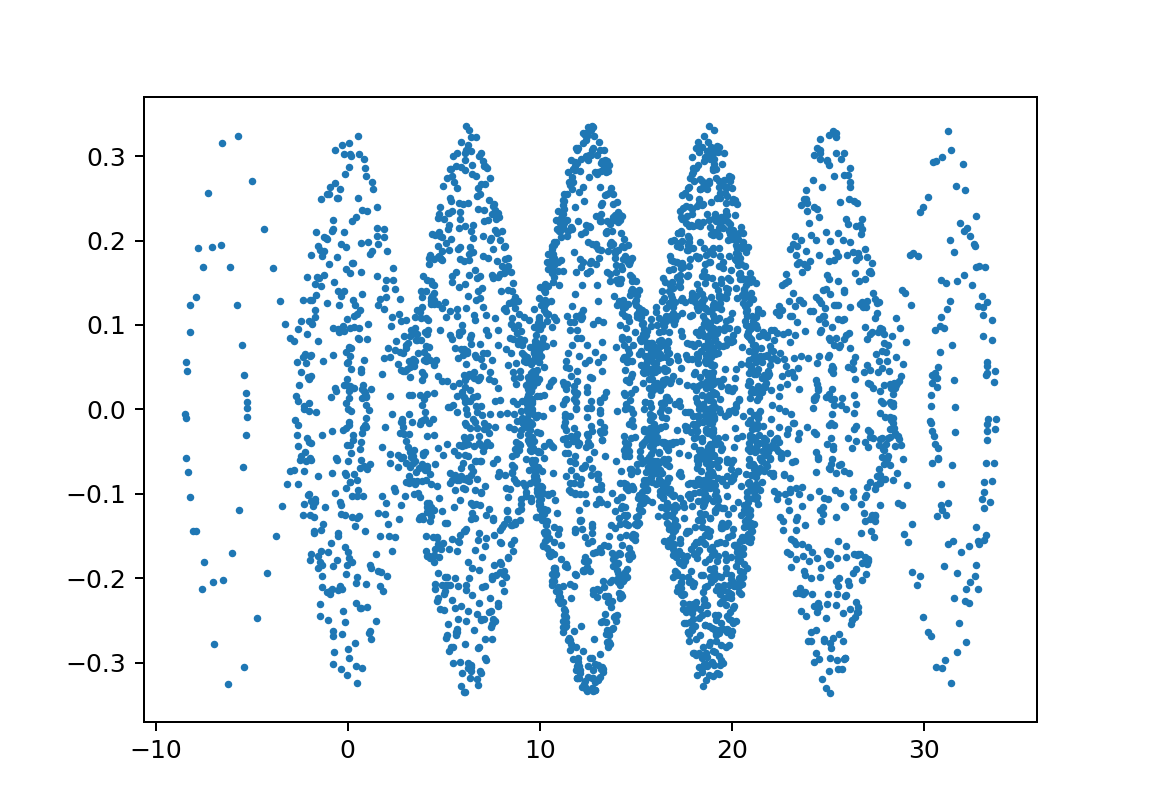
xp2_L1500L2450m110000m21750y011.003
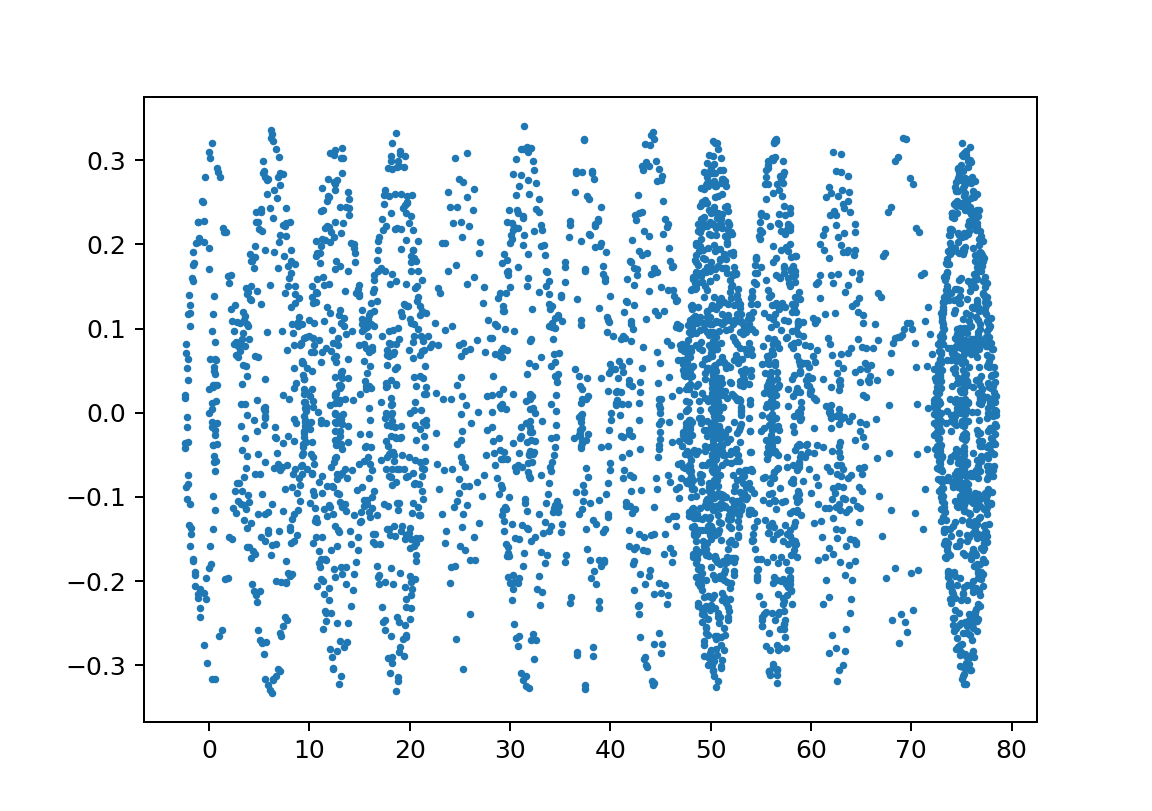
xp2_L1500L2450m110000m21750y011.004
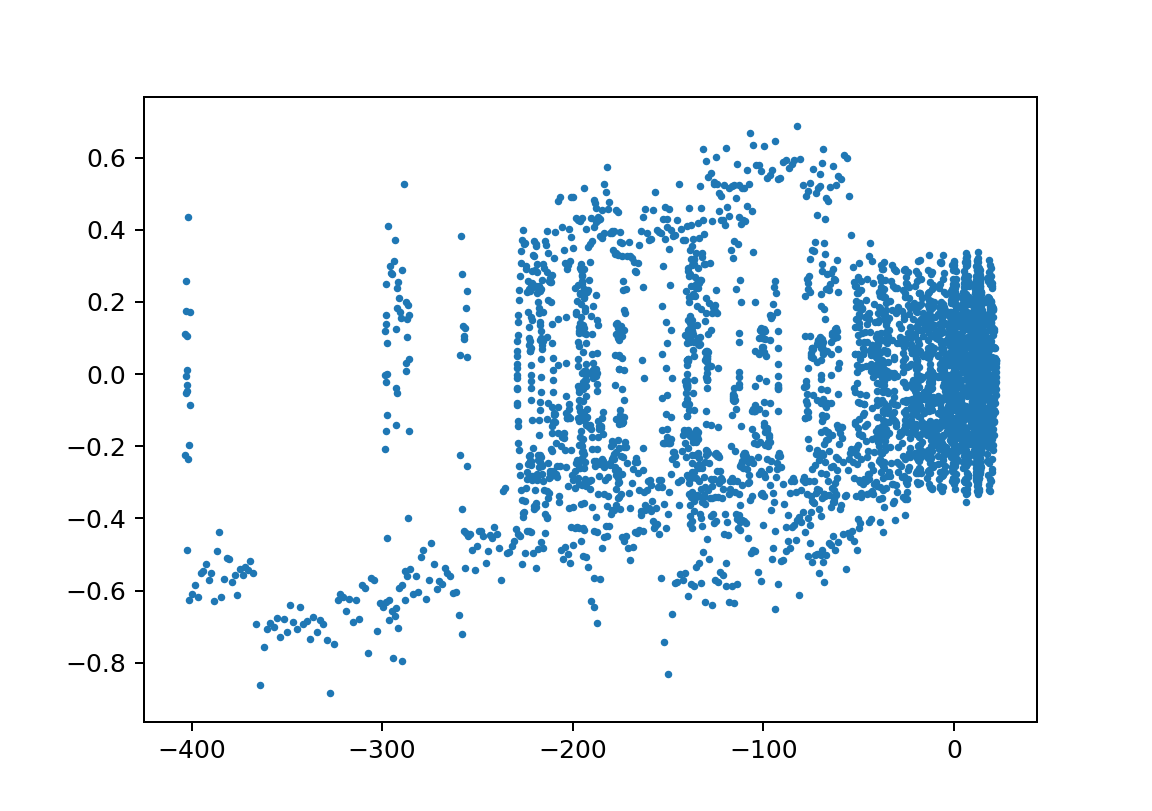
この領域のΘvstの絵はセットで示すと以下のようなものである。
※周期が長い方が見やすいのでそういうのを選んでいますが、基本は似たような絵になっています。
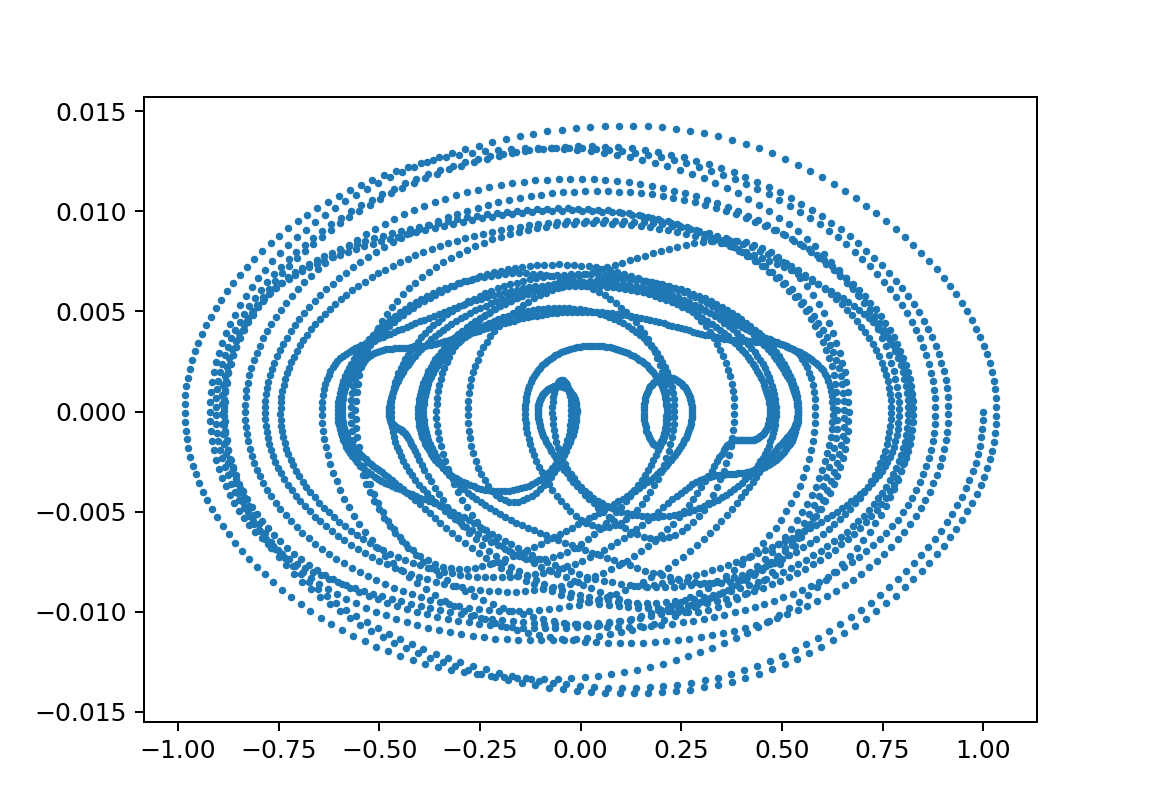
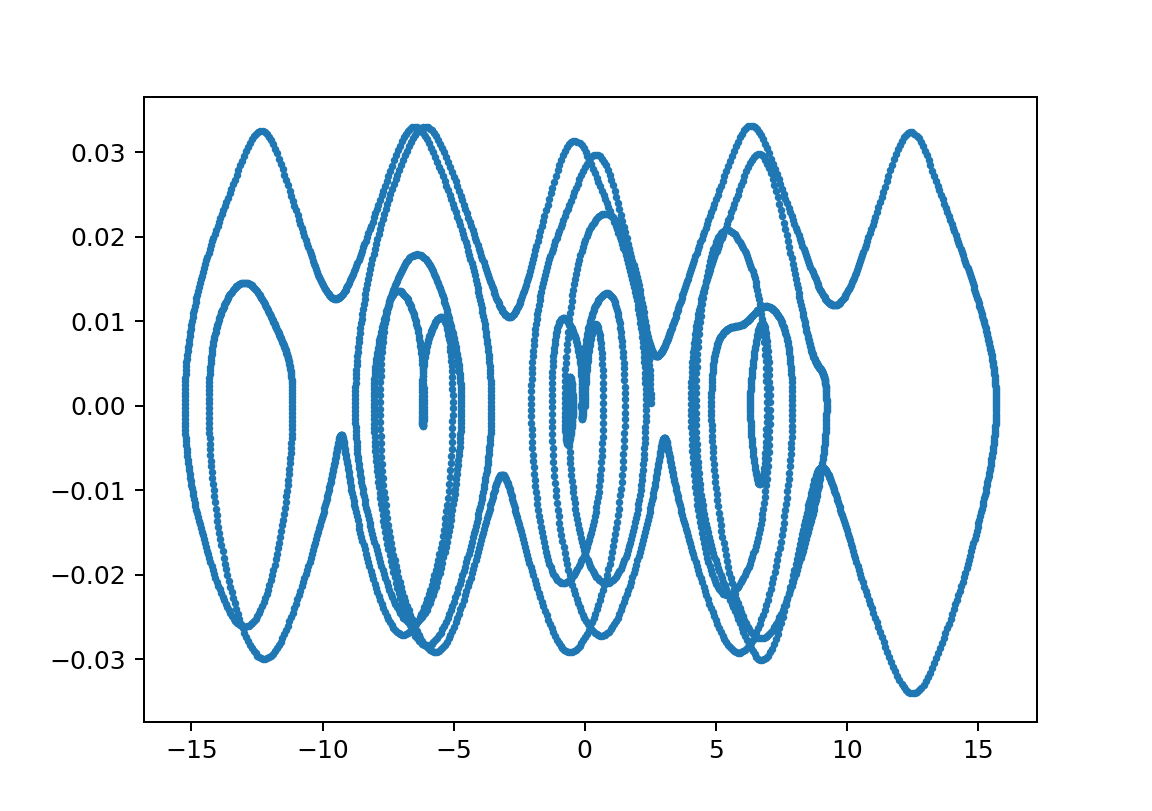
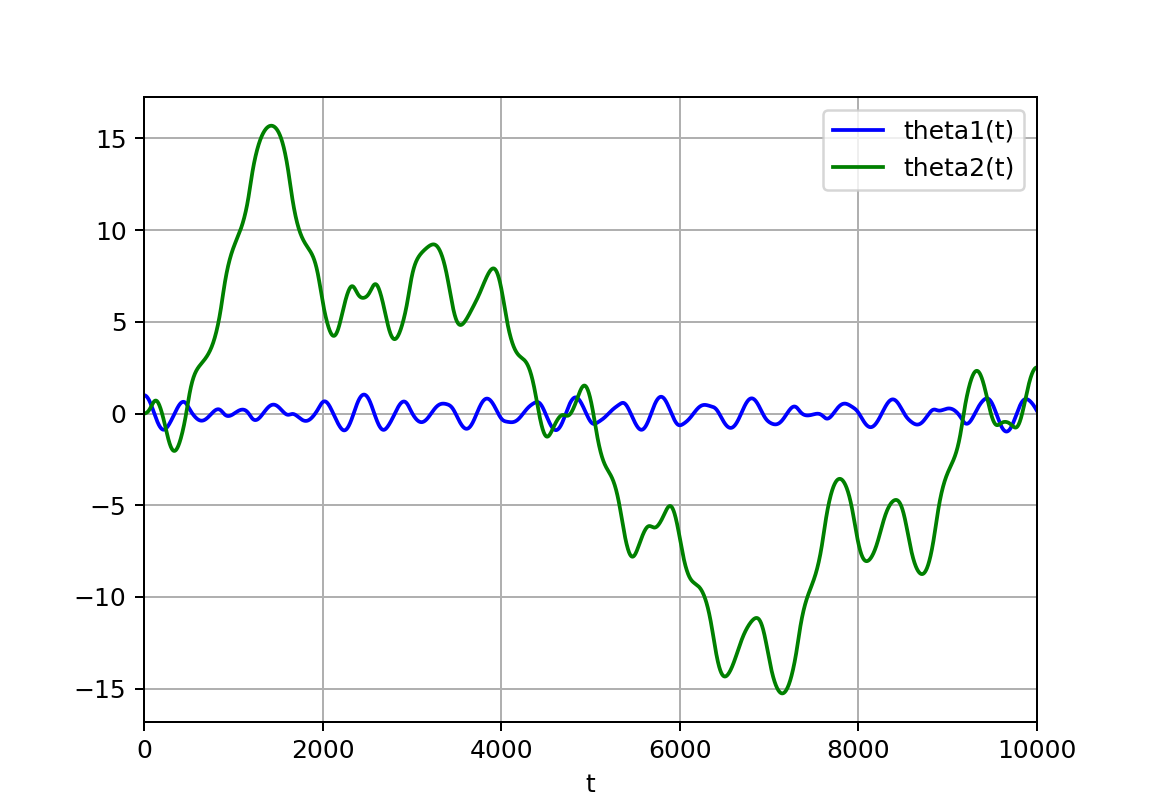
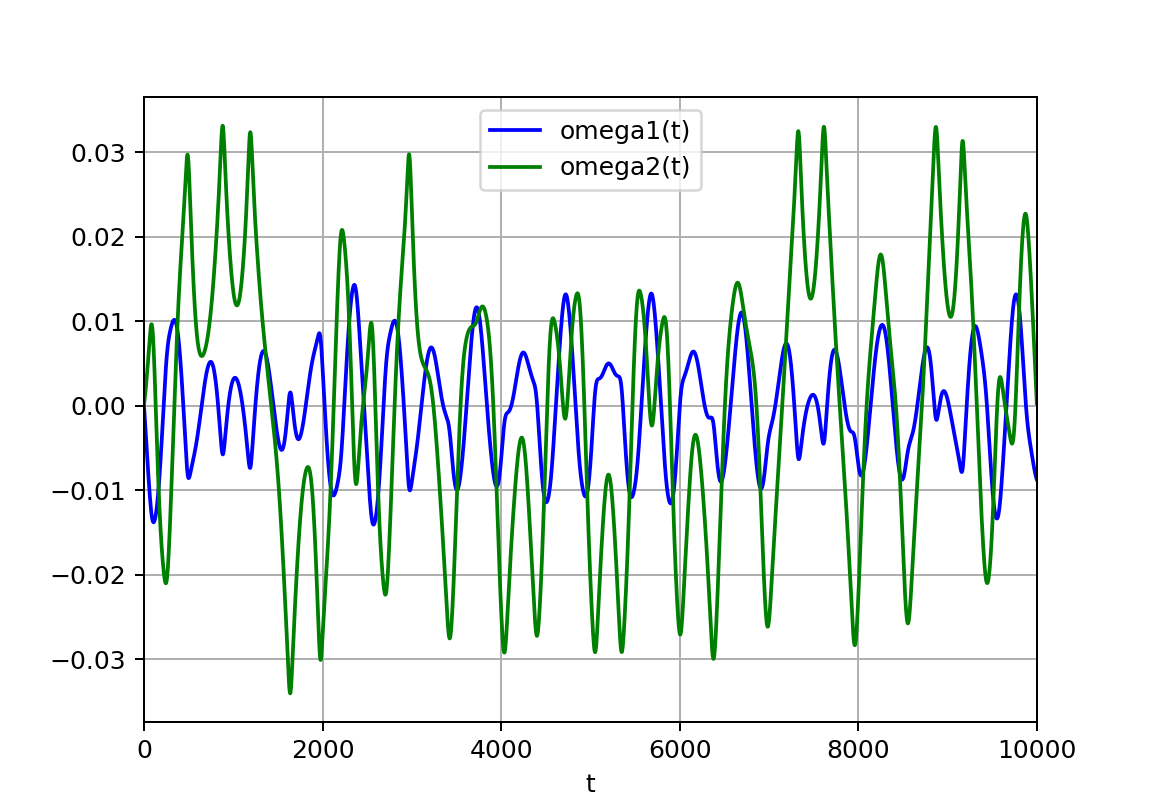
以下、xp2のL2鋭敏性;初期値だけでなく振り子の長さや重さなどに鋭敏に依存する
xp2_L1500L2497m110000m21750y010.9999
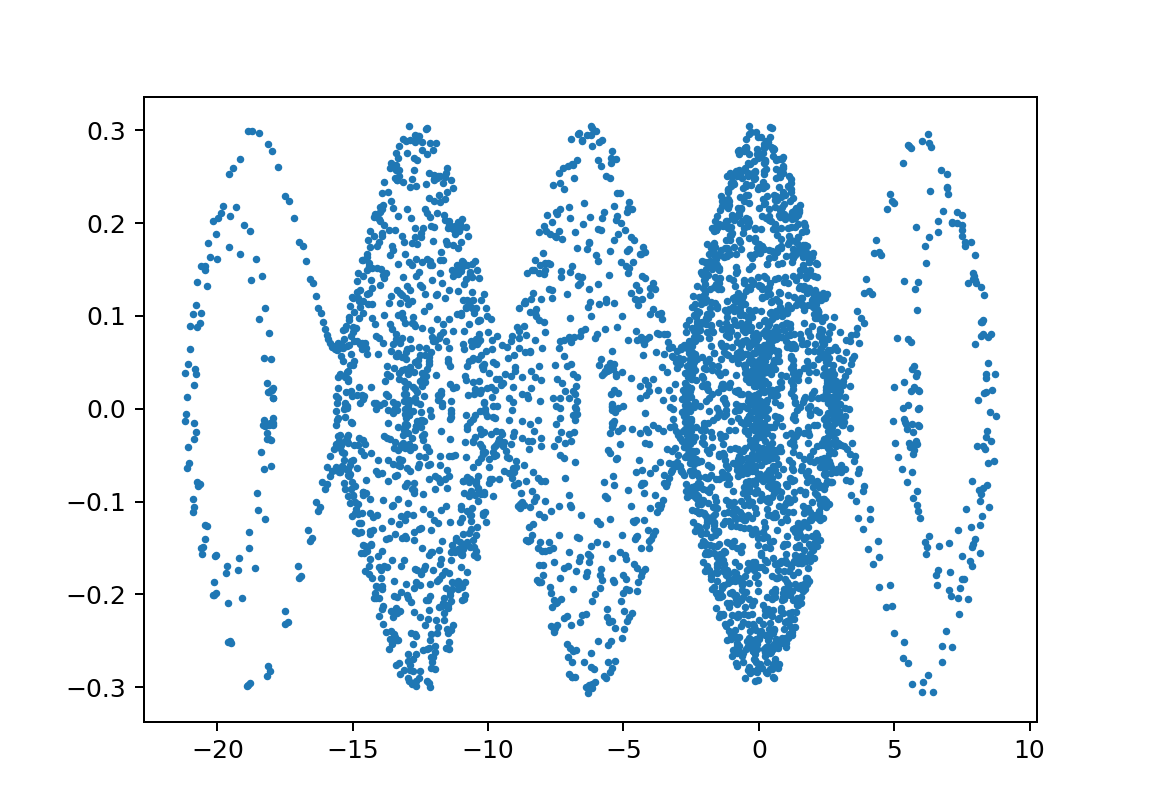
xp2_L1500L2497.01m110000m21750y010.9999
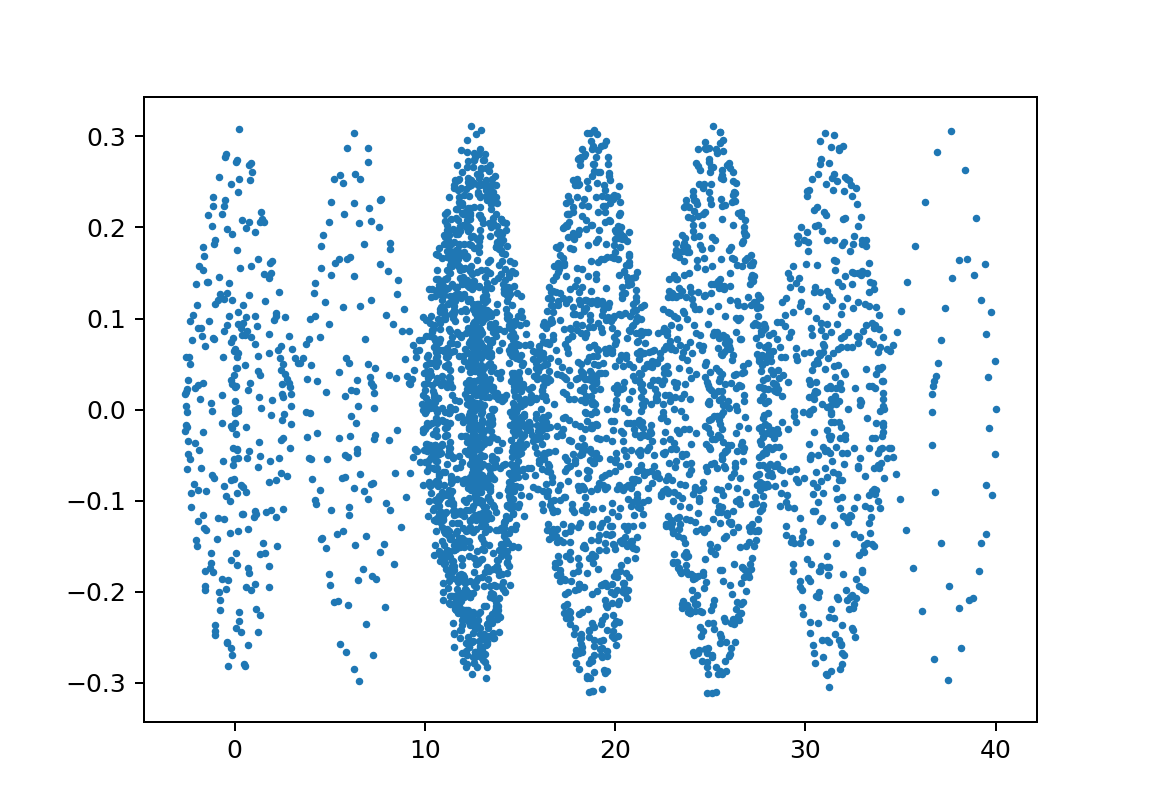
xp2_L1500L2497.1m110000m21750y010.9999
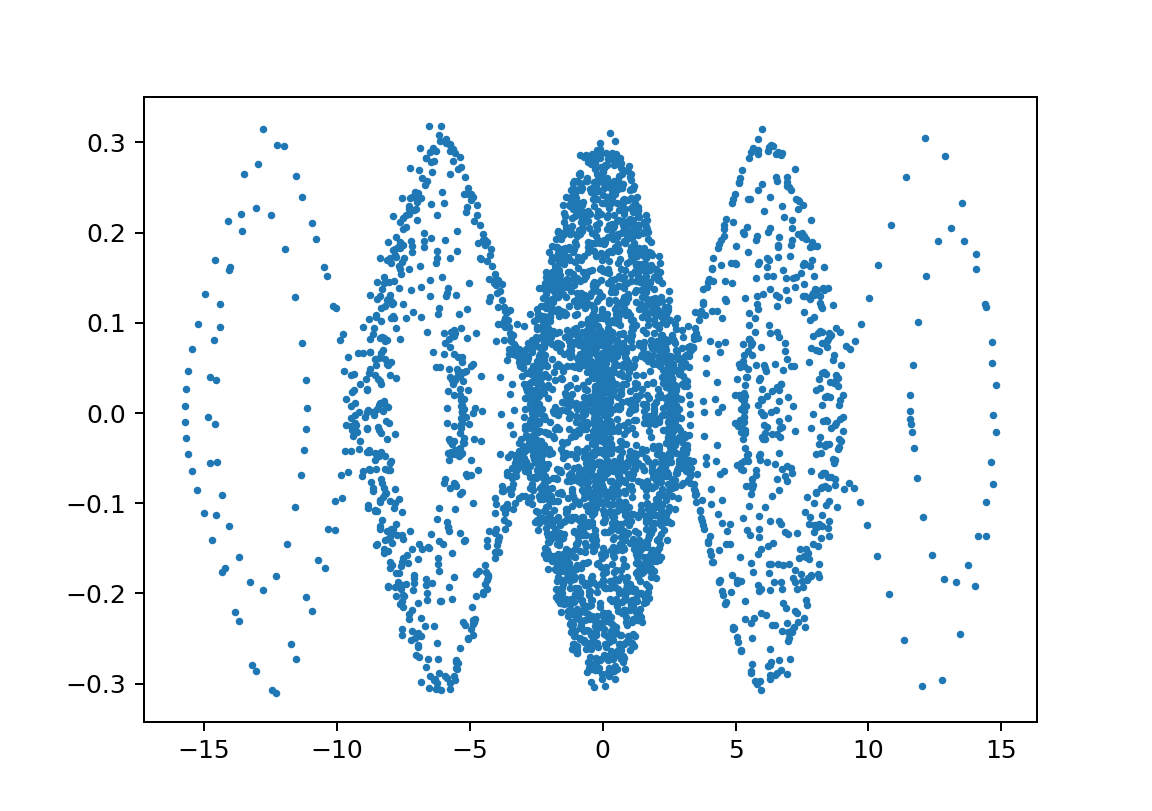
xp2_L1500L2497.5m110000m21750y010.9999
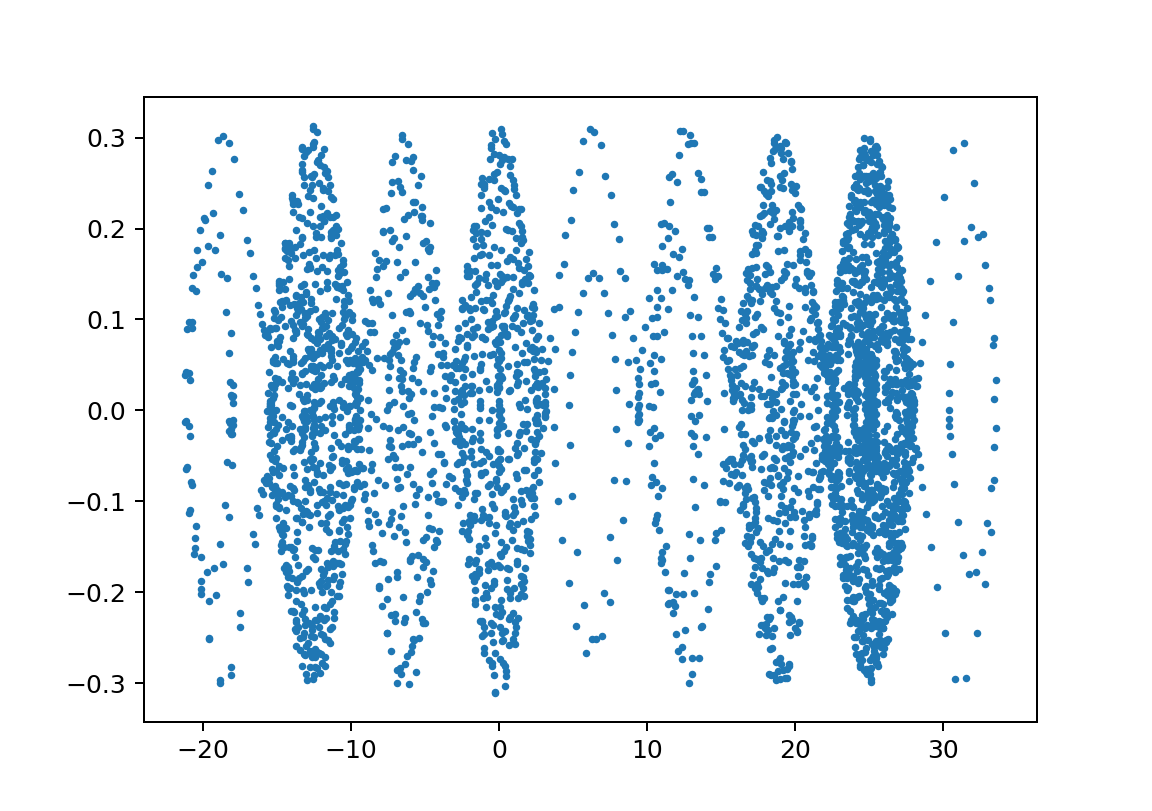
以下安定領域っぽいところでの初期値鋭敏性
。。やはりこれくらいだとカオスではないと云えそう
xp2_L1500000L250000m11000m21000y010.5
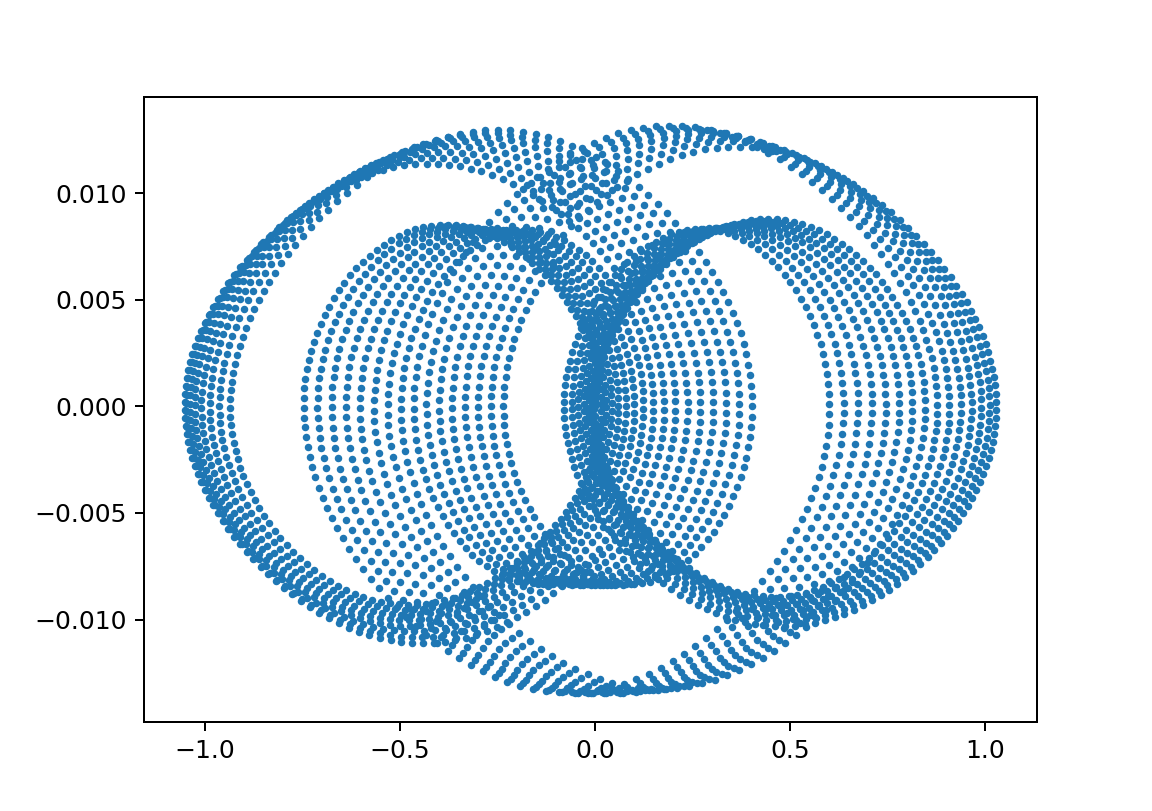
xp2_L1500000L250000m11000m21000y010.5001
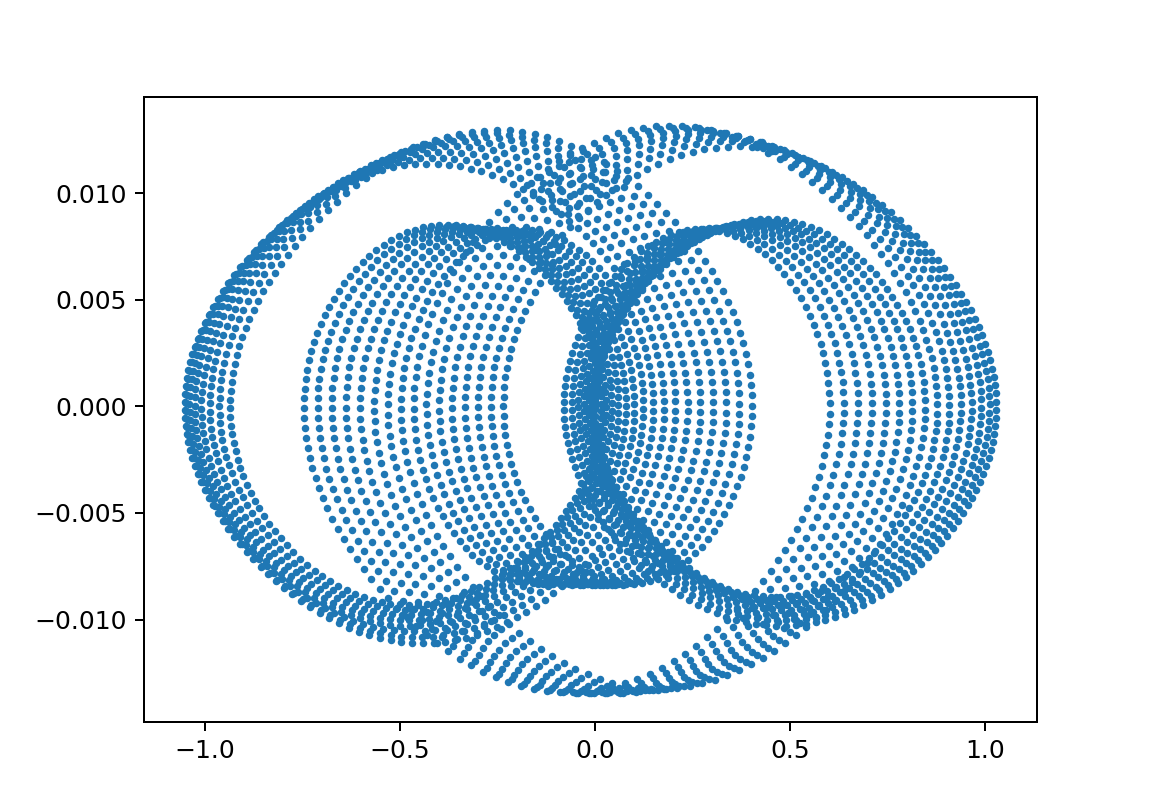
xp2_L1500000L250000m11000m21000y010.51
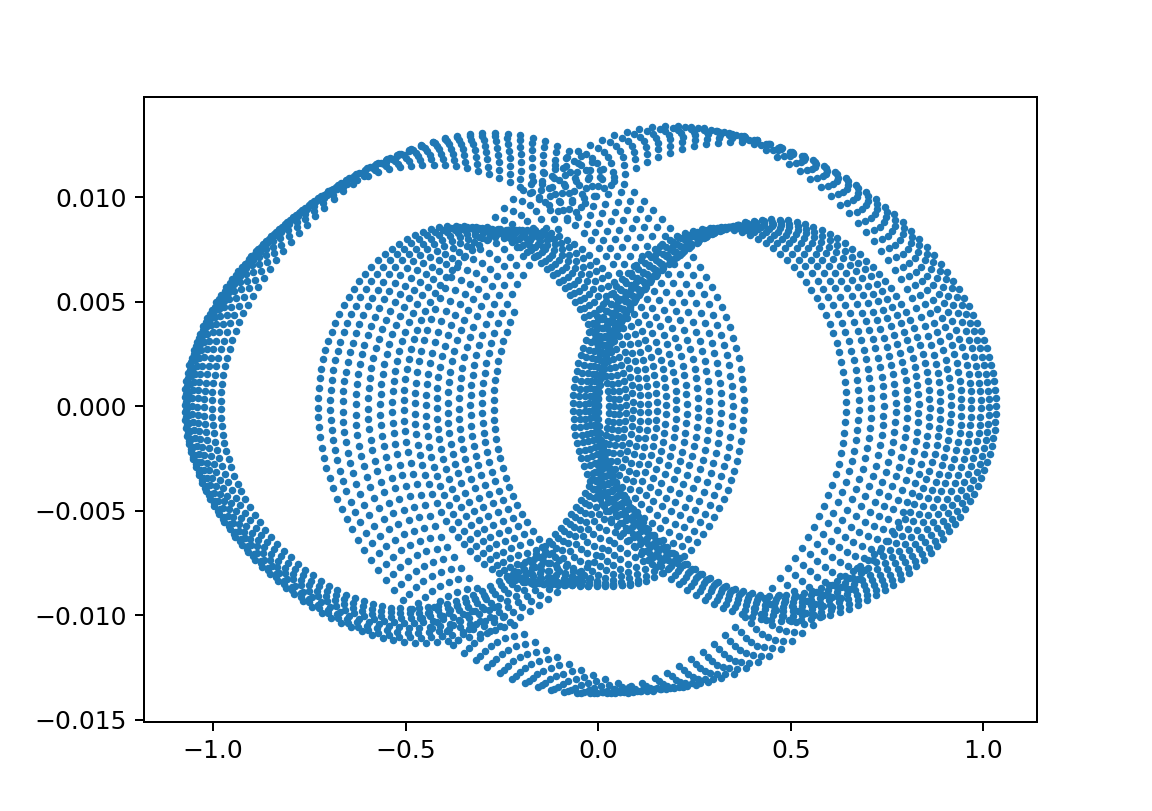
(2)関数のコード
コードはGithubにおきました。
主要な関数とodeintする部分は以下のとおり
def dualPendulum(y, t, L1, L2,g,m1,m2):
theta1, omega1,theta2, omega2 = y
dydt = [omega1,
(-g*(2*m1+m2)*np.sin(theta1)-m2*g*np.sin(theta1-theta2)-2*np.sin(theta1-theta2)*m2* (omega2*omega2*L2+omega1*omega1*L1*np.cos(theta1-theta2))) / (L1*(2*m1+m2-m2*np.cos(2*(theta1-theta2)))),
omega2,
(2*np.sin(theta1-theta2)*(omega1*omega1*L1*(m1+m2)+g* (m1+m2)*np.cos(theta1)+omega2*omega2*L2*m2*np.cos(theta1-theta2))) / (L2*(2*m1+m2 - m2*np.cos(2*(theta1-theta2))))]
return dydt
L1=500
L2=497.01
g=9.8
m1=10000
m2=1750
y01=0.99990
y0 = [y01, 0.0,0, 0.0]
t = np.linspace(0, 10000, 4001)
sol = odeint(dualPendulum, y0, t, args=(L1, L2,g,m1,m2))
x1, p1,x2,p2 = sol.T[0], sol.T[1], sol.T[2], sol.T[3]
ここは入力ミスがなければ動くと思います。
※リンク先のコードはとりあえず動くことを確認のために簡単な振り子の解法をつけています
(3)運動方程式の一考察
運動方程式について
参考の②③④を参考に記載する。
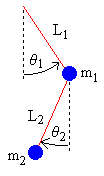
①それぞれの振子の腕の先端に質点が存在するモデルの運動方程式⇒単振り子を連結したモデル@上図のような場合
(m_1+m_2)L_1\theta_1'' + m_2L_2\theta_2''\cos(\theta_1 - \theta_2) + m_2L_2\theta_2'^2\sin (\theta_1 - \theta_2) + (m_1+m_2)g\sin\theta_1=0
L_1\theta_1''\cos(\theta_1 - \theta_2) + L_2\theta_2'' - L_1\theta_1'^2\sin (\theta_1 - \theta_2) + g\sin\theta_2=0
※第二式はwikipediaのものから式全体をL_2で除している
②それぞれの振子の腕の中間に質点が存在するモデル(物理振り子を連結したモデル)の運動方程式⇒均質な棒を二本連結した場合
(m_1+4m_2)L_1\theta_1'' + 2m_2L_2\theta_2''\cos(\theta_1 - \theta_2) + 2m_2L_2\theta_2'^2\sin (\theta_1 - \theta_2) + (m_1+2m_2)g\sin\theta_1=0
2L_1\theta_1''\cos(\theta_1 - \theta_2) + L_2\theta_2'' -
2L_1\theta_1'^2\sin (\theta_1 - \theta_2) + g\sin\theta_2=0
※wikipediaのものを第一項と二項を順番を変えた
ここで大切なことは、①②どちらのモデルも「係数を置き換えると同じ運動方程式である。」ということである。
つまり、第一式は以下の置き換えで読み替えることができる。
m_2 ⇒ 2m_2 (1)
第一項のみ
m_2 ⇒ 4m_2
一方、第二式は、
L_1 ⇒ 2L_1 (2)
の読み替えで同じ方程式となる。
運動方程式全体としては、上記の(1)(2)の読み替えをやって、さらに第一式第一項のm_1の係数を1/2すればよいことが分かる。
まとめ
・単振り子連結の二重振り子の数値解をやってみた
・二重振り子のカオスな振舞を観察した
・棒連結の二重振り子について運動方程式の類似性を見た
・次回は棒連結の二重振り子の解を解いて、実際にUnityで動かしてみる予定
おまけ
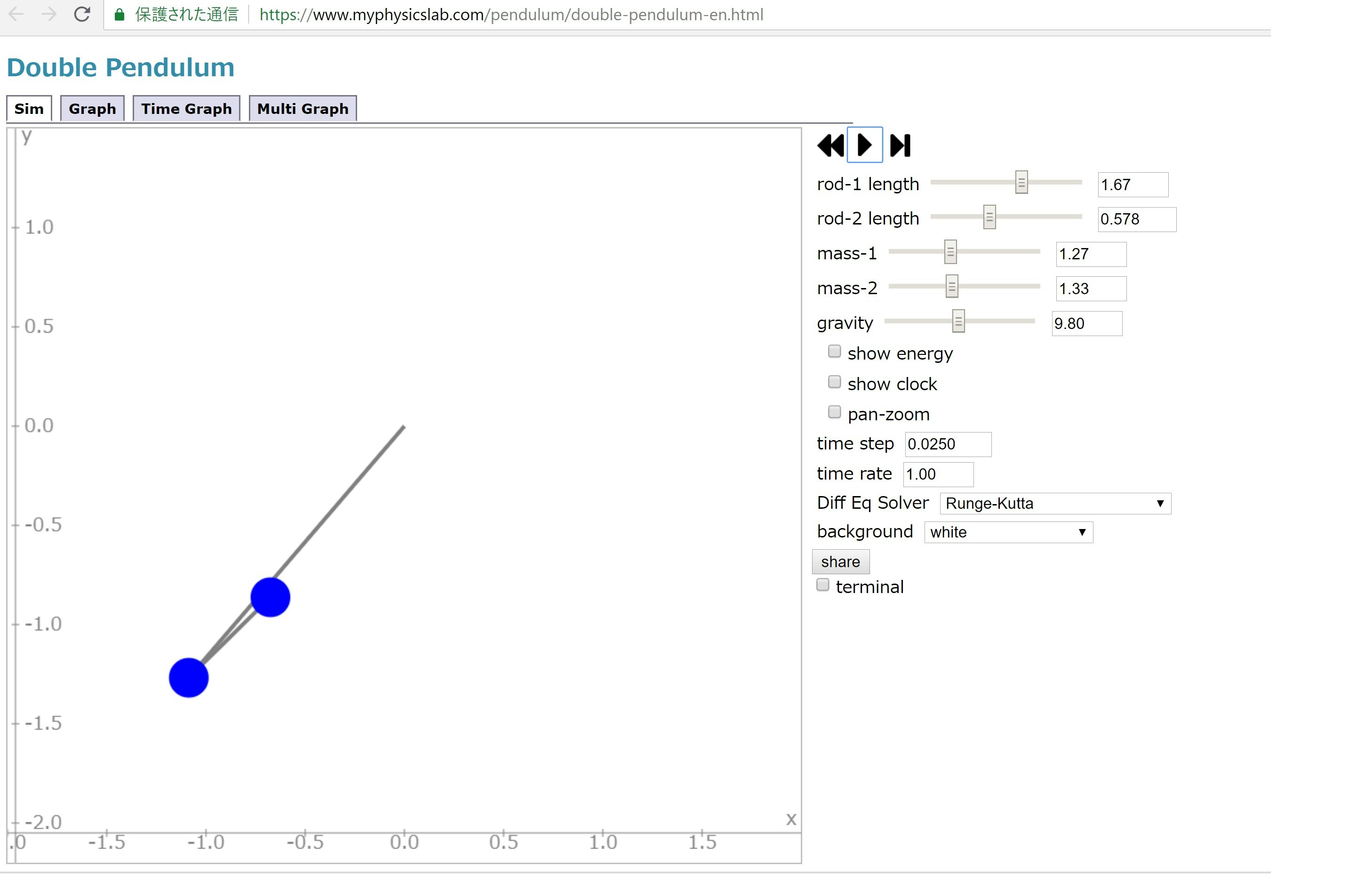
シミュレーションについて
今回のおもりのある場合の単振り子の二重振り子は以下のサイトでシミュレートできる。
使い方は、
①停止した状態で振り子のおもりをドラッグするとつまめるので適当な位置に置く
②右のパラメータを適当に設定して、▶を押すと動く
③上段のタグを選ぶとグラフなどを描画しながら動く様子が見られる