世の中は、「感染数は多いけど、重症者は少ないので大丈夫」というご意見が多い。
まあ、実際感染者は若者中心で高齢者の感染は少ないようだ。
とはいえ、重症化は感染から遅れてやってくるのでどのように増えてくるのかをグラフを描いて確認してみようと思う。
方法は、このところやっているのとほぼ同様な方法で以下のとおりです。
①厚労省からデータ入手
②重症数をデータ化(5月7日までは未公表)
③感染数と重症数を同じグラフ上にプロット
結果は、以下のとおり得られました。
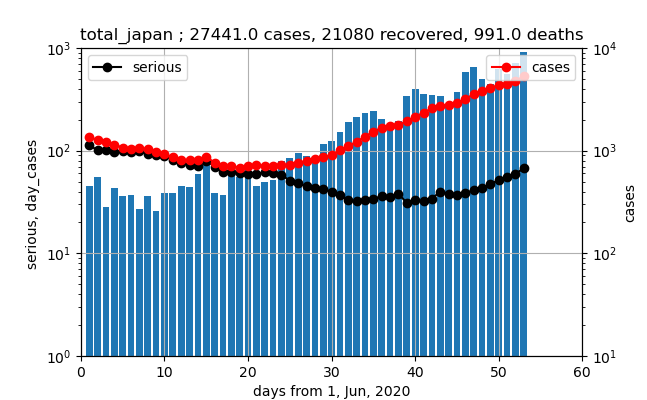
全国
以下のとおり、対数プロットで見ると、
①現存感染数(赤いプロット)と現存重症数(黒いプロット)は約18日遅れで、しかも800:30程度の比で同じようなグラフである
②新規感染数(青のバーグラフ)と現存感染数は同じような推移で、比は約1000:6000である
①から、重症化率=約4%
②から、入院日数=約6日程度(実際の入院日数とは異なります)
また、本来は第一波の余波の影響を無視した分析なので、正しくやろうとすれば第一波分のデータを差し引くなどの処理が必要ですが、今回は無視することとします。
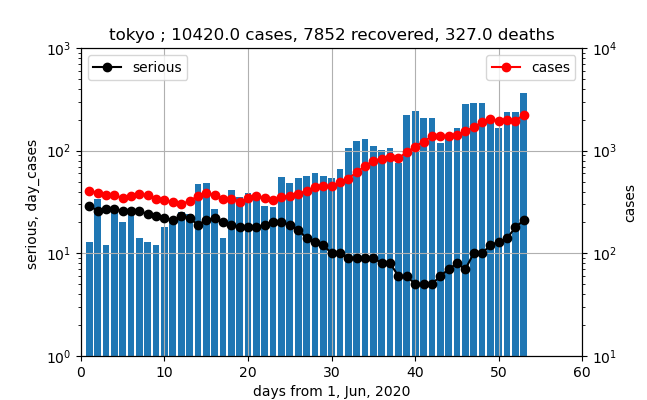
東京
東京のデータも赤いプロット、黒いプロット、そして青いバーグラフが類似しています。ただし、重症数が6月24日辺りから大幅減(直線の傾きが変わったので退院基準などの変更だと思います)となり、7月10日辺りから急激に増加しているのが分かります。東京の場合は、傾きが現存感染数や新規感染数の傾きより大きいので、重症化率が増加しているように見えます。
また、東京アラート解除が6月11日なので、6月24日の約二週間前になります。
ということはありますが、ここでも重症化は18日程度遅れでほぼ似たような曲線を描くことが分かります。重症化率=1-2%程度です。
入院日数=約7日程度です。
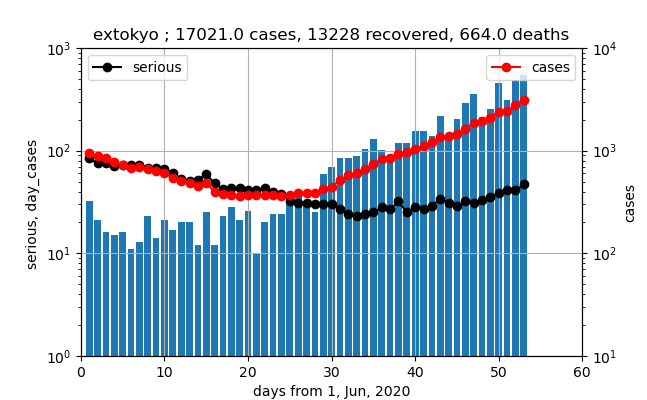
東京以外
このデータでは、重症数の立ち上がりはだらだらしていて、傾きが現存感染数の直線より小さいです。つまり、第一波の余波が大きく、そのため傾きが小さくなっているか、実際に重症化率が下がっているかまだ不明です。これから立ち上がって平行な直線に乗ってくると思われます。
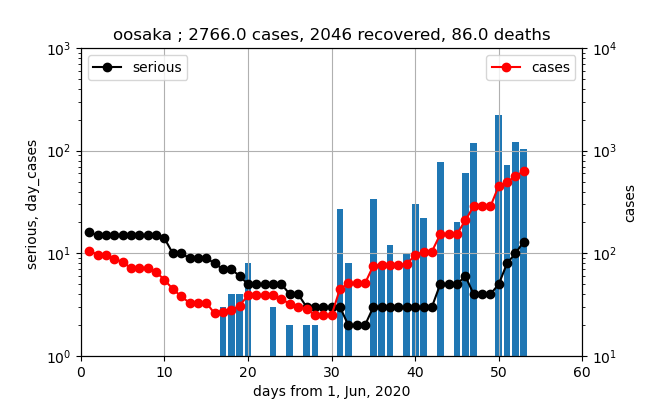
大阪(厚労省データは荒れているが)
このデータは誤差が大きそうです。しかし、それでも上記の3つのグラフと比較すると、以下の議論に記載したような一定の傾向が見えます。
議論
ここでは、医療崩壊について、考察しておこうと思います。
主にグラフの傾きがこれからの傾向を示してくれます。
東京は、現在現存感染数は2000人で、重症数21人です。
傾きから、30日程度で10倍に増加すると懸念されます。つまり、20000人、特に重症数200人です。ECMOなどの設備と人の準備状況はどうなんだろうと心配になります。何の対策もしなければ、60日後は200000人、2000人です。なんの対策もしていなければ、医療崩壊してしまいそうです。
一方、大阪のグラフの特徴は傾きが大きいというところにあります。
上記の大阪以外のグラフでは、10倍/30日でしたが、ここでは10倍/20日程度の傾きを持っています。医療崩壊を起こさないために、あと20日後に今の10倍になるということを考えて早めの施策が必要です。
現存感染数と重症数を重ねて表示する
一応、ずれを示したので、以下グラフを平行移動して重ねてみた。
重症数データのプロットを縦軸10倍とデータそのものを2倍し、横軸を19日ずらしてみると以下のように重なった。
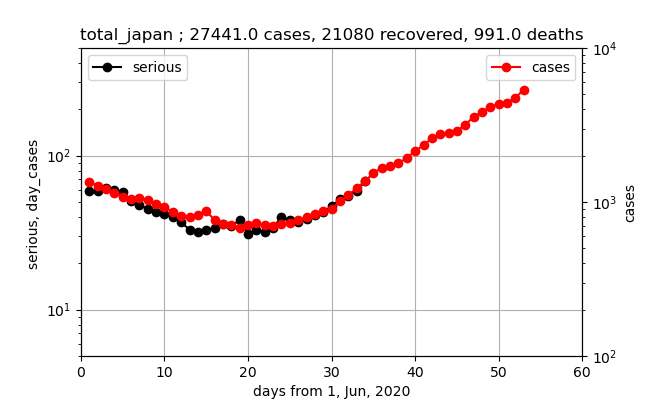
つまり、今後全国は以下のように赤いプロットに乗って、重症数が増加しそうである。
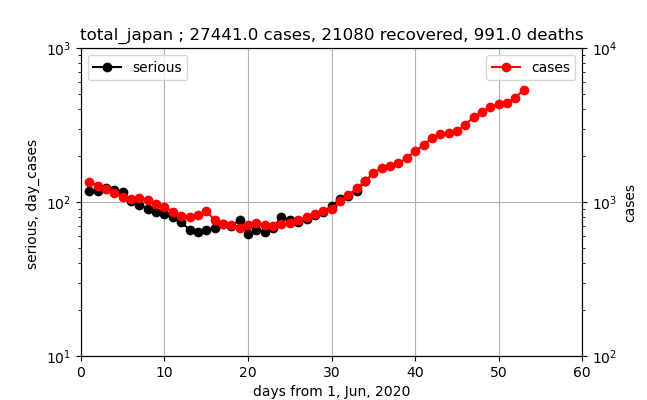
東京は以下のとおり、重ならないが、これは重症数が大きく減少し、徐々に増加しているためであり、今後赤い線に乗ってきそうである。
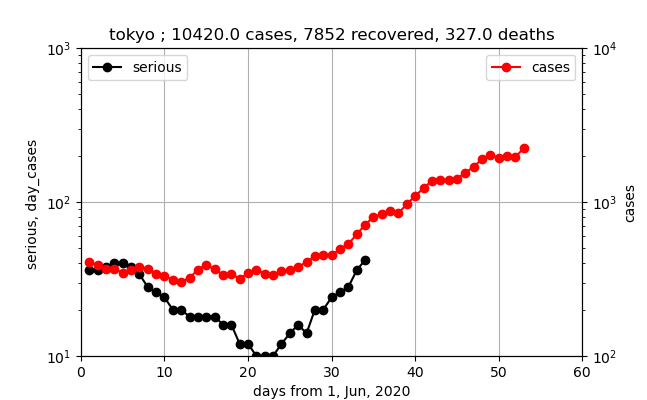
東京以外は以下のとおり、だいたい乗っているが、少し大きめであり、第一波が影響していそうであるし、東京の寄与と合わせて全国として乗っているのでその程度の誤差なのであろう。
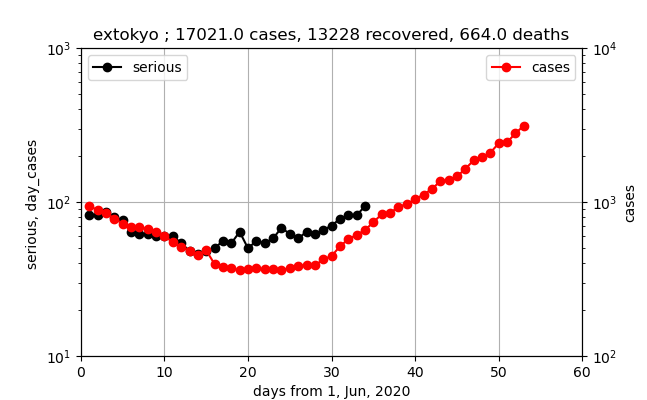
同じスケールで大阪も見ると以下のとおりであまり一致しませんが、データが荒れているので様子を見ようと思います。
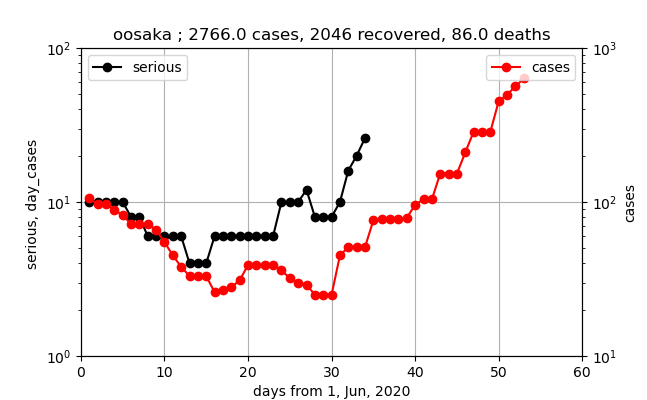
こうしてみると、重症数は、たぶん定義もまちまちであり、統一的な数値を求めるのは難しそうである。
それでも、全体として重症化率は一定値となるか、弱毒化の指標として減少するかを見ていくことは有意義であると思う。
今、このスケールでグラフが重なったことから、上述の目の子換算と異なりますが、グラフから求められる(現存感染数当たりの)重症化率は以下のとおりです。
重症化率=1/20=約5%
程度であると推定できる。
上記は、データを2倍して一桁ずらしたが、単に重ねるには、以下のように縦軸の表示範囲をずらしても重なるので、示しておく。
※生データを2倍するとはなにごとだと怒られそうなので。。。
まとめ
・感染数と重症化の関係を対数グラフを描いて見た
・**重症化率は、約5%**であった
・重症数は現存感染数グラフの変化と相関して、現存感染数の19日遅れのグラフに(重症化率倍すると)乗る事が分かった
・全国と東京、東京以外、そして大阪と重症数の変化の特徴が異なる部分もあり、医療崩壊の状況を見極めるためにも、今後もウォッチする必要があると考える
・国内のデータは、発生も少なく、全体に日々データの精度がいまいちであり、他国の例も含めて検証したいと思う
おまけ(コード)
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
data = pd.read_csv('data/covid19/test_confirmed.csv',encoding="cp932")
data_r = pd.read_csv('data/covid19/test_recovered.csv',encoding="cp932")
data_d = pd.read_csv('data/covid19/test_deaths.csv',encoding="cp932")
data_s = pd.read_csv('data/covid19/test_serious.csv',encoding="cp932")
confirmed = [0] * (len(data.columns) - 1)
day_confirmed = [0] * (len(data.columns) - 1)
confirmed_r = [0] * (len(data_r.columns) - 1)
day_confirmed_r = [0] * (len(data.columns) - 1)
confirmed_d = [0] * (len(data_d.columns) - 1)
diff_confirmed = [0] * (len(data.columns) - 1)
confirmed_s = [0] * (len(data.columns) - 1)
days_from_1_Jun_20 = np.arange(0, len(data.columns) - 1, 1)
beta_ = [0] * (len(data_r.columns) - 1)
gamma_ = [0] * (len(data_d.columns) - 1)
daystamp = "531"
city,city0 = "東京以外","extokyo"
skd=1 #2 #1 #4 #3 #2 #slopes average factor
# データを加工する
t_cases = 0
t_recover = 0
t_deaths = 0
for i in range(0, len(data_r), 1):
if (data_r.iloc[i][0] == city): #for country/region
print(str(data_r.iloc[i][0]))
for day in range(1, len(data.columns), 1):
confirmed_r[day - 1] += data_r.iloc[i][day]
if day < 1+skd:
day_confirmed_r[day-1] += data_r.iloc[i][day]
else:
day_confirmed_r[day-1] += (data_r.iloc[i][day] - data_r.iloc[i][day-skd])/(skd)
t_recover += data_r.iloc[i][day]
for i in range(0, len(data_d), 1):
if (data_d.iloc[i][0] == city): #for country/region
print(str(data_d.iloc[i][0]) )
for day in range(1, len(data.columns), 1):
confirmed_d[day - 1] += float(data_d.iloc[i][day]) #fro drawings
t_deaths += float(data_d.iloc[i][day])
for i in range(0, len(data), 1):
if (data.iloc[i][0] == city): #for country/region
print(str(data.iloc[i][0]))
for day in range(1, len(data.columns), 1):
confirmed[day - 1] += data.iloc[i][day] - confirmed_r[day - 1] -confirmed_d[day-1]
if day == 1:
day_confirmed[day-1] += data.iloc[i][day]
else:
day_confirmed[day-1] += data.iloc[i][day] - data.iloc[i][day-1]
for i in range(0, len(data_d), 1):
if (data_d.iloc[i][0] == city): #for country/region
print(str(data_d.iloc[i][0]) )
for day in range(1, len(data.columns), 1):
confirmed_s[day - 1] += float(data_s.iloc[i][day])*2 #ここで重症数を2倍している
def EMA(x, n):
a= 2/(n+1)
return pd.Series(x).ewm(alpha=a).mean()
day_confirmed[0]=0
df_c = pd.DataFrame(day_confirmed)
df_c.to_csv('data/day_comfirmed_{}.csv'.format(city0))
m=15
dc_m = EMA(day_confirmed,m) #EMA(day_confirmed,m) #df_c.rolling(m).mean()
dc_m.to_csv('data/day_comfirmed_EMAmean{}_{}.csv'.format(m,city0))
dc_m_l=dc_m.values.tolist()
tl_confirmed = 0
for i in range(skd, len(confirmed), 1):
if confirmed[i] > 0:
gamma_[i]=float(day_confirmed_r[i])/float(confirmed[i])
else:
continue
tl_confirmed = confirmed[len(confirmed)-1] + confirmed_r[len(confirmed)-1] + confirmed_d[len(confirmed)-1]
t_cases = tl_confirmed
# matplotlib描画
fig, ax1 = plt.subplots(1,1,figsize=(1.6180 * 4, 4*1))
ax3 = ax1.twinx()
lns1=ax3.plot(days_from_1_Jun_20[1:], confirmed[1:], "o-", color="red",label = "cases")
lns4=ax1.plot(days_from_1_Jun_20[1:35], confirmed_s[20:55], "o-", color="black",label = "serious") #ここで横軸を19日ずらしている
lns_ax1 = lns4
labs_ax1 = [l.get_label() for l in lns_ax1]
ax1.legend(lns_ax1, labs_ax1, loc=2)
ax3.legend(loc=1)
ax1.set_title(city0 +" ; {} cases, {} recovered, {} deaths".format(t_cases,t_recover,t_deaths))
ax1.set_xlabel("days from 1, Jun, 2020")
ax1.set_ylabel("serious, day_cases ")
ax3.set_ylabel("cases")
ax3.set_xlim(0,60)
ax1.set_xlim(0,60)
ax3.set_ylim(10,1000)
ax1.set_ylim(1,100) #1500
ax3.set_yscale('log')
ax1.set_yscale('log')
ax1.grid()
plt.pause(1)
plt.savefig('./fig/original_data_{}_{}_new.png'.format(city,daystamp))
plt.close()