【将棋AI】「将棋AIで学ぶディープラーニング」を読む♪～【神の一手】を目指す

第廿八夜は、やはり方策ネットワークだけで強い将棋AIを作りたいということで、[前回の方法を踏まえて](https://qiita.com/MuAuan/items/1ce5d3a375f6c93e544d)挑戦してみました。その結果、LesserKaiには圧勝できる将棋AIが出来たのでまとめておこうと思う。 ###やったこと （０）そもそも一致率について （１）最近の方策・価値ネットワークを方策ネットワークにして学習 （２）強さを見る ###（０）そもそも一致率について 将棋AIの学習を始めてこの方、どうも一致率が低いよな～と思っている。 ということで、一致率どの程度なのか調べてみると、参考のような記事が見つかる。 以前も書いたが山岡さんのFloodgateの対戦データとの一致率は方策が43.7％価値が70.6％とのことで、これでレーティング３１００のGPSfishと同程度ということである。 一方、プロは優秀なソフトとの一致率がどの程度かというと、参考②のような記事がある。この記事は女流棋士が急激に成長しているという記事ですが、そこでソフトとの一致率を評価として使っているのが目を見張ります。そして、以下の数字が出されています。 以下参考②からの引用です。

・豊島棋聖：54.0％(15036/27842)
・永瀬七段：52.3%（8954/17106）
・豊島棋聖対局相手：51.6％(14348/27761)
・永瀬七段対局相手：51.4％(8704/16923)
・里見女流四冠：50.3％(4171/8290)
・里見女流四冠対局相手：50.2％(4163/8290)

以下が女流棋士の成長を表している一致率です。

・里見女流四冠（2014-）：50.3％(4171/8290)
・里見女流四冠対局相手(2014-)：50.2％(4163/8290)
・里見女流四冠（-2014）：48.8％(3318/6795)
・里見女流四冠対局相手（-2014）：45.7％(3111/8290)

これらの数字は、どうやら「解析は最新のQhapaq(レーティングサイト基準でレート4300超)で行っています。」らしいです。もちろん、これらの数字と今回のFloodgateの棋譜からの学習で得られたTestデータとの一致率と単純に比較はできません。しかし、同様な種類のものだということは言えると思います。
そういう意味では、DeepLearningでの一致率の目標も、この５０％超えということになりそうです。
※実際は、レーティングの高いソフト間の一致率がどの程度かはこの評価の適用できる範囲の信用性をどの程度とみるかの目安になると思いますが、それは出来ればいつかやりたいと思います
【参考】
① 将棋AIの進捗 その25(自己対局による強化学習の経過)
②将棋ソフトから見る昨今の女流棋士の急激な成長@コンピュータ将棋 Qhapaq
###（１）最近の方策・価値ネットワークを方策ネットワークにして学習
まず、最近の方策・価値ネットワークでは、学習は以下のように方策ネットワークが０．４５をこえるものが出てきた。
※こちらの記事は別に書こうと思う

network	loss	policy_accuracy	value_accuracy	note
Quad22_1617	2.951929	0.43959206	0.679099	epoch=10、22層※1
Try24_1617	3.076979	0.44028142	0.69179535	epoch=5、24層※1
Try30_1617	2.78209	0.45002618	0.6764027	epoch=12、34層※1
Policy	1.7603214	0.42603874	－	epoch=26、13層
Try30_1617	1.69182	0.44690228	－	epoch=6、34層
Try30_1617	1.65441	0.4464856	－	epoch=7、34層
※1；$Loss=1.6Loss_{policy}+0.4Loss_{value}$としている

このTry30_1617のネットワークを利用して以下のような方策ネットワークを作成して学習させてみた。結果は上記の表の最下段の通りです。

from chainer import Chain
import chainer.functions as F
import chainer.links as L
from pydlshogi.common import *

ch = 192

class Block(Chain):
    def __init__(self):
        super(Block, self).__init__()
        with self.init_scope():
            self.conv1 = L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
            self.conv2 = L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
            self.conv3 = L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)

    def __call__(self, x):
        h1 = F.relu(self.conv1(x))
        h2 = F.relu(self.conv2(h1))
        h3 = self.conv3(h2)
        return F.relu(x+h3) #x+h2

class PolicyNetwork(Chain):
    def __init__(self, blocks = 10):
        super(PolicyNetwork, self).__init__()
        self.blocks = blocks
        with self.init_scope():
            self.l1=L.Convolution2D(in_channels = 104, out_channels = ch, ksize = 3, pad = 1)
            self.l2=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
            for i in range(1, 10):
                self.add_link('b{}'.format(i), Block())
            # policy network
            self.policy=L.Convolution2D(in_channels = ch, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1, nobias = True)
            self.policy_bias=L.Bias(shape=(9*9*MOVE_DIRECTION_LABEL_NUM))

    def __call__(self, x):
        h = F.relu(self.l1(x))
        h = F.relu(self.l2(h))
        for i in range(1, 10):
            h = self['b{}'.format(i)](h)
        # policy network
        h_policy = self.policy(h)
        u_policy = self.policy_bias(F.reshape(h_policy, (-1, 9*9*MOVE_DIRECTION_LABEL_NUM)))
        return u_policy

###（２）強さを見る
以前は強いと思っていたPolicyに圧勝しました。
※ここではepoch=7のパラメータを使っています

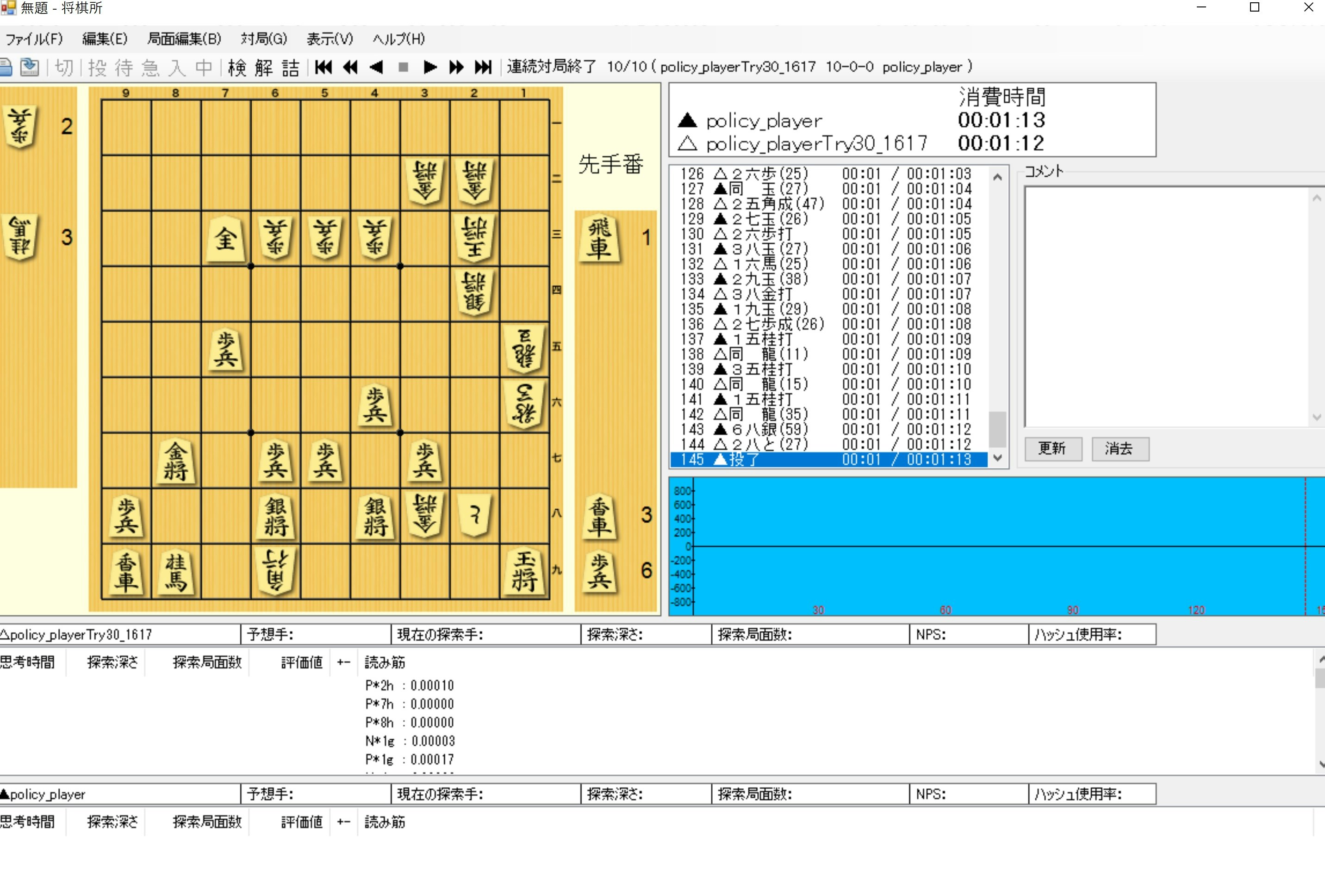
そして、方策ネットワークには強敵なLesserKaiにも圧勝
※LesserKaiは探索局面数１００，０００を超えることもあるので、指すのは早いが十分読んでいます。

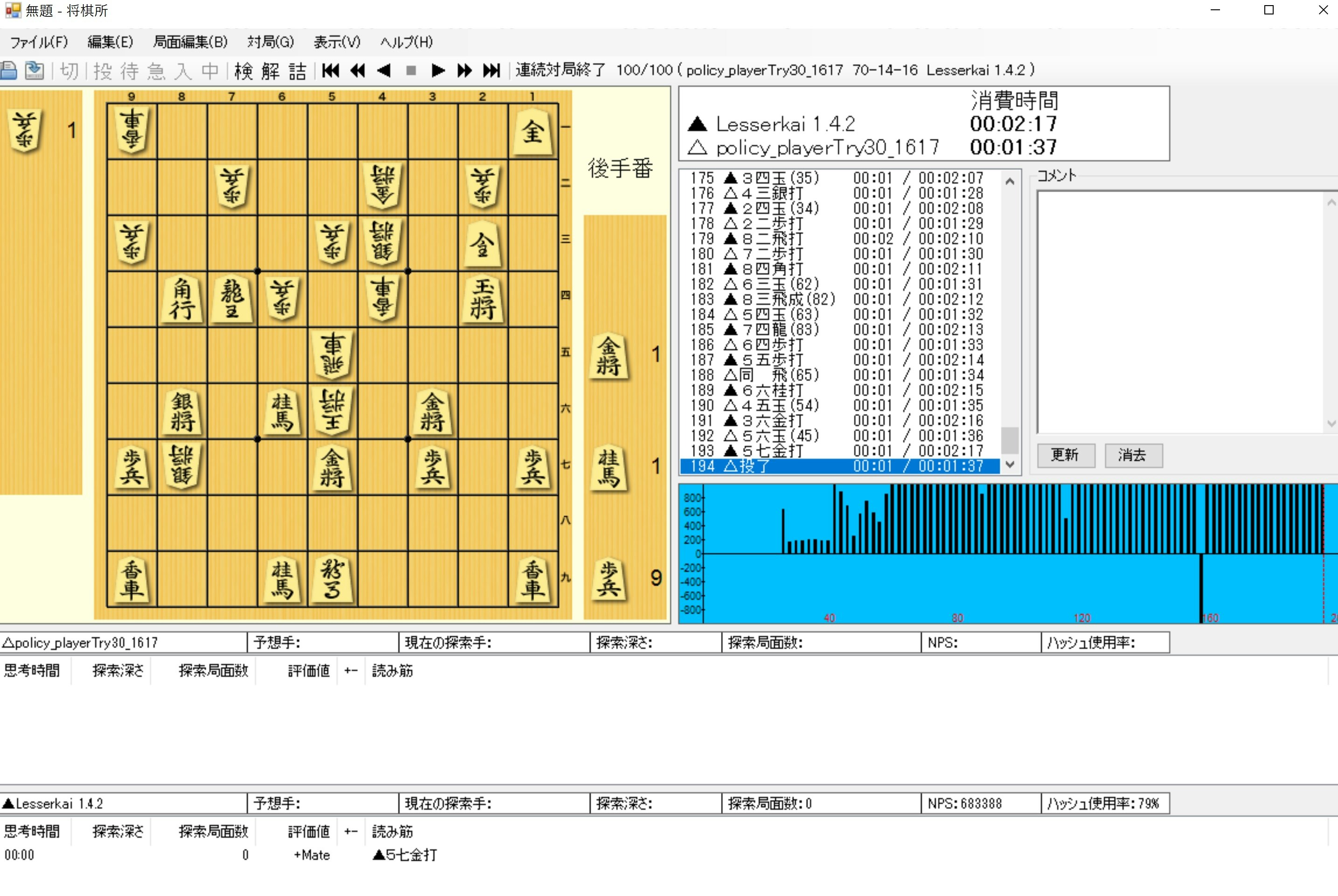
そして、Gikou2D1にも対戦してみました。

ということで、レーティングはLesserKai（７１８）とGikou2D1（１５１２）の間ということで、だいたい１０００（９３０－１０３０）位です。
ということで、この程度の一致率ではまだまだだとわかります。

それにしても、サクサク打ってLesserKaiに勝利するのは気持ちいいものです。

ところで、MCTSベースの将棋AIと方策ネットワークのみで次の指し手を指す将棋AIでは本質的に異なるものです。前者はあくまで従来のモンテカルロ木探索をサポートして指し手を決めているのに対して後者は次の一手をその盤面から一意に決定する将棋AIだからです。そして、盤面から一意に最善手があるのかどうかは実は自明な話では無いと思います。だから、本質的にドメイン知識というか相手の棋力や盤面のその後の発展に依存する因子があるのだ（そもそも将棋には大逆転の要素がある）とすると、この一意に次の一手を打つのは限界があるのだろうと思います。そのあたりが見えてくると面白いと思います。

###まとめ
・一致率のだいたいの目安を見た
・方策ネットワークのみでレーティング１０００程度になった

・方策ネットワークの一致率は現在４４．６％であるが、目標は５０％辺りのようだ