第廿四夜も、レーティングのおはなしです。
どうも、ウワンも誤解していましたが、レーティングはその集団で独自に決まるもので、特に標準的なものでないということのようです。
基本的なレーディングの考え方は以下のWikipediaのイロレーティングによるようです。そして手合いごとの勝敗に基づいたレーティングの上昇・下降はいろいろな計算式が派生しているようです。ここでは基本に立ち戻ってイロレーティングを使って早見表を作成し、現状のソフトレーティングを見積もってみたいと思います。
※今回のお話はウワンの妄想に基づいて展開しています。利用する際は自己責任でご利用、引用してください。
【参考】
⓪[イロレーティング＠Wikipedia](https://ja.wikipedia.org/wiki/%E3%82%A4%E3%83%AD%E3%83%AC%E3%83%BC%E3%83%86%E3%82%A3%E3%83%B3%E3%82%B0)
①[早見表](http://kishibetsu.com/hayami.html)
②[思考深度制限した技巧２の２４R](http://www.uuunuuun.com/single-post/2018/07/31/%E6%80%9D%E8%80%83%E6%B7%B1%E5%BA%A6%E5%88%B6%E9%99%90%E3%81%97%E3%81%9F%E6%8A%80%E5%B7%A7%EF%BC%92%E3%81%AE%E6%A3%8B%E5%8A%9B)
[コンピュータ将棋 まとめサイト](https://www.qhapaq.org/shogi/)
###やったこと
（１）イロレーティングから早見表を導出する
（２）プロとその他の上昇・下降公式の考え方
（３）対戦によるソフトレーティングを予測する
###（１）イロレーティングから早見表を導出する
イロレーティングでは、次の3点を基本とする。
・ゲームの結果は一方の勝ち、一方の負けのみとし、引き分けは考慮しない（0.5勝0.5敗と扱うものとする）。
・200点のレート差がある対局者間では、レートの高い側が約76パーセントの確率で勝利する。
・平均的な対局者のレートを1500とする。
3人の対局者 {\displaystyle A,B,C} について {\displaystyle A} が {\displaystyle B} に勝利する確率を {\displaystyle E_{AB}} 、
{\displaystyle B}が {\displaystyle A}に勝利する確率を {\displaystyle E_{BA}} などと定める。
対局者間の勝率について次のような仮定を置く。
{\displaystyle {\frac {E_{AC}}{E_{CA}}}={\frac {E_{AB}E_{BC}}{E_{BA}E_{CB}}}} {\displaystyle {\frac {E_{AC}}{E_{CA}}}={\frac {E_{AB}E_{BC}}{E_{BA}E_{CB}}}}
2人の対局者 {\displaystyle A} 、 {\displaystyle B} の現在のレートを {\displaystyle R_{A}} および {\displaystyle R_{B}} としたとき、
それぞれが勝利する確率 {\displaystyle E_{A}}、 {\displaystyle E_{B}} は以下の式で算出される。
{\displaystyle E_{A}={\frac {1}{1+10^{(R_{B}-R_{A})/400}}}}
{\displaystyle E_{B}={\frac {1}{1+10^{(R_{A}-R_{B})/400}}}}
上記の二つの式は一般化するとレート差を
\Delta R (=R_{A}-R_{B})
とすると、レート差がある場合の勝率は、以下のように書ける。ここで上位者ならばレート差は正であり、下位者であれば負の値となる。
{\displaystyle E_{\Delta R}={\frac {1}{1+10^{-\Delta R/400}}}}
これを実際に計算してみると以下の通り早見表が作成できる。
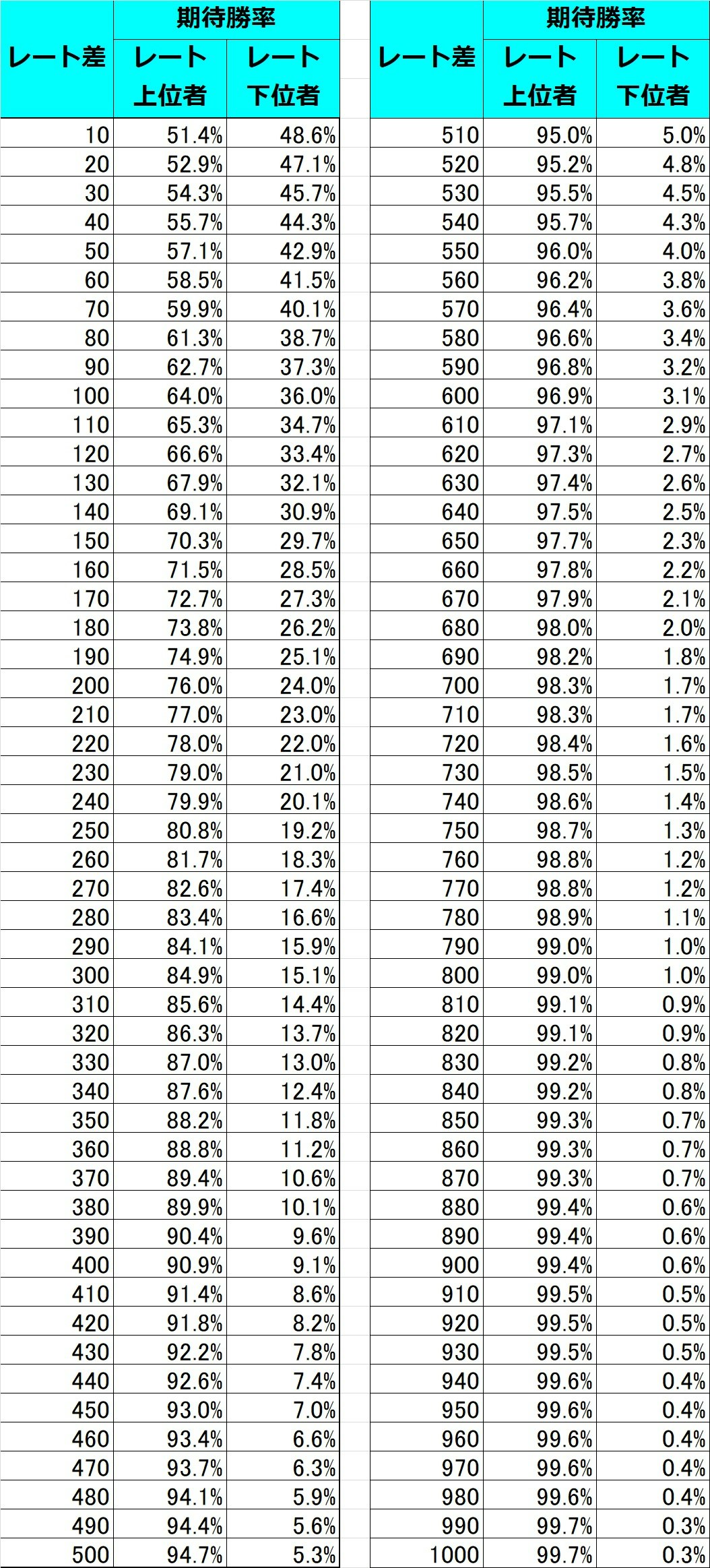
そして、この関数を横軸をレート差として負から正に動かしたときの期待勝率をグラフ化すると以下のとおりとなる。
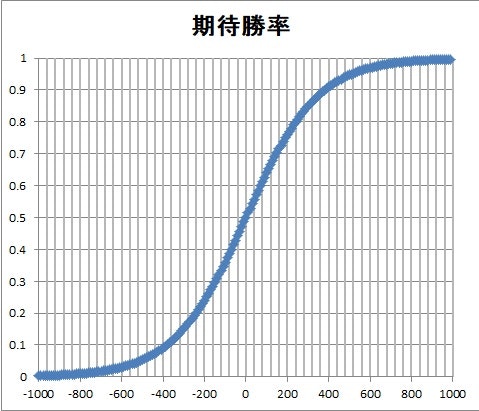
このグラフから自分から見て、勝負になるのはだいたい±200位のレート差であり、
・200点のレート差がある対局者間では、レートの高い側が約76パーセントの確率で勝利する。
が満たされている。
さらにこの関数形は以前山岡さんのところで議論されていた、評価値と勝率の関係と同じ、シグモイド関数である。
E_{a}={\frac {1}{1+e ^{{-a/600}}}}
ここで$a$は評価値（相手に対する正負の相対値）、$E_{a}$は勝率
【参考】
・将棋でディープラーニングする その22(評価値と勝率の関係)
以前は（ウワンはここを抑えてはいないが）elmoの評価関数に依存して規格化係数は６００や７５０辺りの数字であった。今回は定義として$４００/ln10\fallingdotseq 174$が使われている。しかし、本質的にレーティング（すなわち評価値）の差を勝率に変換するという意味においては全く同等であると考察される。
ただし、底を変換してシグモイド関数として表すと以下のとおり係数は大きく異なる。
{\displaystyle E_{\Delta R}={\frac {1}{1+e ^{{‐\Delta R/174}}}}}
※今後この辺りを突き詰めれば本来リーズナブル（自然）なレーティングの定義を導入できるのかもしれない
###（２）プロとその他の上昇・下降公式の考え方
Wikipediaの上記参考サイトにも記載がある。
実際に何局か対局した結果、 {\displaystyle A} の勝ち数が {\displaystyle S_{A}} であった場合、 {\displaystyle A} のレートを以下のように補正し、
新たなレート {\displaystyle R_{A}^{\prime }} とする（ {\displaystyle E_{A}} は各対局の勝利する確率を足し合わせる）。
{\displaystyle R_{A}^{\prime }=R_{A}+K(S_{A}-E_{A})}
ここで、 Kは定数値であり、プロレベルでは16、通常は32をとることが多い。
上式は変形すると以下の形になる
E_{A}= S_{A}-\frac{1}{K}({R_{A}}^{\prime }-R_{A})
なんとなく、前出の勝率のシグモイド関数から近似的に得られたようにも見える。
※残念ながら、ウワンにはこの係数の謎は理解不能であった。きちんと理解するためには多数回シミュレートしてしっかり理解するのがよいと思うが次回以降に持ち越す
###（３）対戦によるソフトレーティングを予測する
昨夜に比べて、イロレーティングという理論として理解が深まったので、昨夜の結果に基づいて再度ResnetS40のレーティングを求めてみる。
結果は、
Gikou2 D1 1512 +17/-9
に対して、４勝６敗なので、－４０～ー１００位で昨夜と変わらない。
###まとめ
・イロレーティングから早見表を作成した
・イロレーティングの定義は評価値から勝率を算出するロジックと類似している
・対戦前はレーティングが、そして対戦中は評価値が期待勝率を与える
・対戦後の新しいレーティングの評価式の導出が不明である