第十四夜は、そもそも強いとか弱いとかってどうやって判定するのということについて、本書には記載ないけど、山岡さんのブログから引用しつつ解説しようと思う。
【参考】
①[仮説検定でプログラムが有意に強くなったか検証する](http://tadaoyamaoka.hatenablog.com/entry/2017/06/14/203529)
②[25-2. 二項分布を用いた検定@BellCurve](https://bellcurve.jp/statistics/course/9490.html)
###解説したいこと
（１）１３Layerの将棋AIはLesserKaiより強い
（２）二項分布を用いた検定と将棋AIの強さ
###（１）１３Layerの将棋AIはLesserKaiより強い
昨夜のところで、１３Layerの将棋AIが強くなってきて、LesserKaiに８：２で勝ったので、LesserKaiよりは強くなったと記載した。
しかし、ほんとなの？？と聞かれるとたぶんというしかない。そこで、ちゃんと統計的に強くなったと云いたいので今夜はここを記載するために、５０回ほど対戦させて結果が統計的にどうなのかを記載しようと思う。
まず、結果は以下のとおりであった。
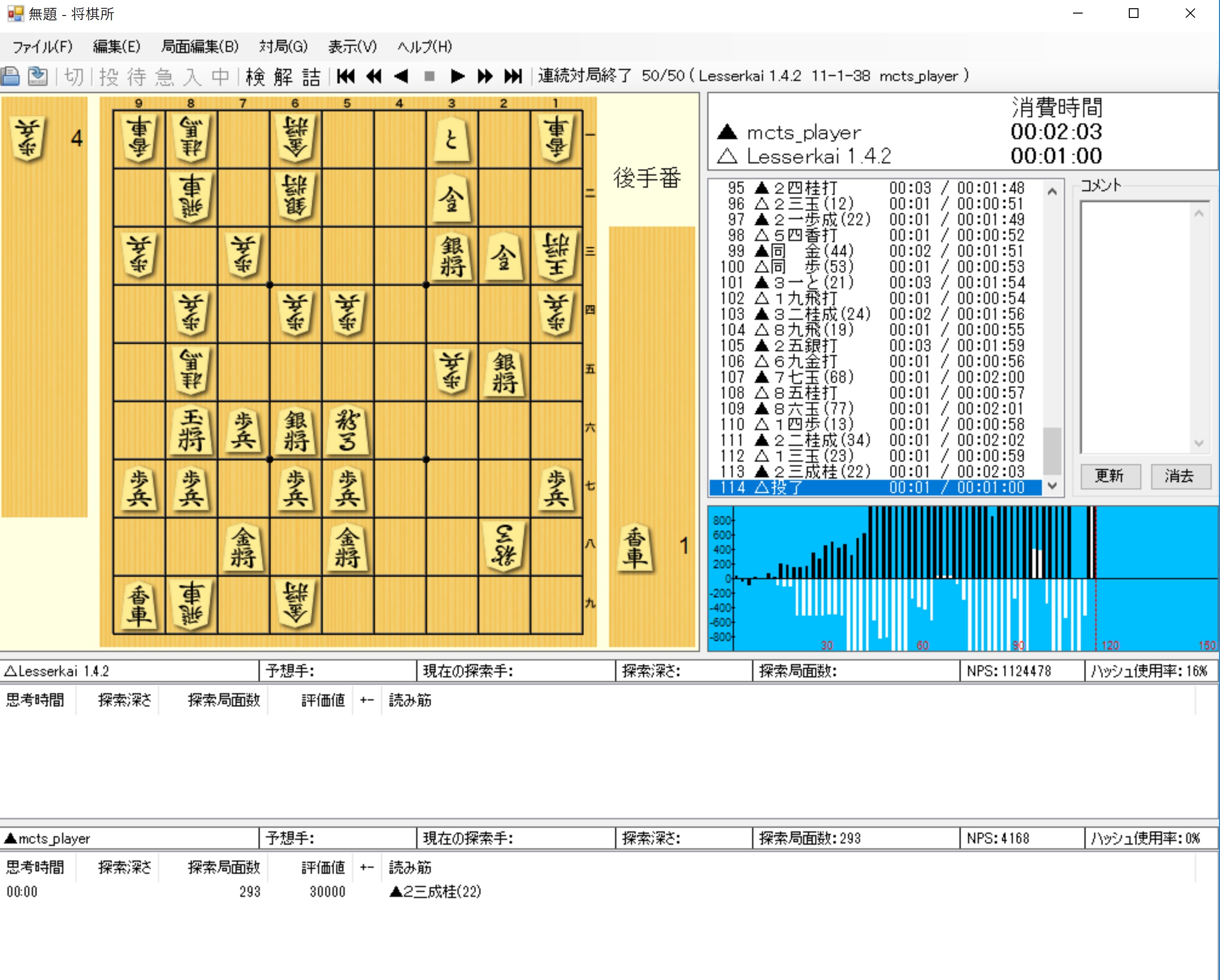
つまり、５０回対戦して、３８－１－１１で勝利した。この数字はほんとに強いといえるのかをチェックしようと思う。
###（２）二項分布を用いた検定と将棋AIの強さ
参考①で山岡さんが式まで示しているので、それを使ってやればいいのだけど、どうもウワンはもともとどこからこの式が来たか気になるので、参考②から引用をしたいと思います。
参考②によれば、
「例題：
あるサイコロを12,000回投げたときに1が2,200回出ました。このサイコロはどの目も等しく出る歪みのないサイコロといえるでしょうか。」
に対して、
「サイコロを投げて1が出るか、出ないかという試行は2種類の結果しか得られないので、サイコロをn回投げたときにx回1が出る確率f(x)は二項分布に従います。」
ということで、こういう風に二者択一の場合は二項分布に従い、二項分布による検定を行えばよいことが分かります。
将棋の場合も勝つか負けるかの二択なので、やはり二項分布に従います。
検定は以下の手順で実施します。
「対局結果から強いかの検定には以下の式で計算する。」＠山岡さん
１．仮説を立てる
帰無仮説；H_0 ：P=P_0(=0.5)
つまり、勝率は０．５である。
サイコロは、
「このサイコロを12,000回振ったときに1が出るのは2,000回（=12,000/6）である」
対立仮説；H_1：P>P_0
勝率は０．５より大きい
サイコロは
「このサイコロを12,000回投げたときに1が出るのは2,000回ではない」
２．有意水準を設定する
α＝０．０５とします。
３．適切な検定統計量を決める
というわけで、今回は以下のような二項分布の検定統計量になります。
二項分布の場合、Xを確率変数とすると「期待値np、分散np(1-p)」であり、統計量を以下のように規格化すると、その分布は標準正規統計に従う分布になる。
z=\frac{X-np}{\sqrt{np(1-p)}}
この式を変形すると
z=\frac{X/n-p}{\sqrt{p(1-p)/n}}
つまり、このzは標準正規分布（平均０、分散１の正規分布）に従う。
ここで、
r=X/n;勝率
n;試行回数(対戦回数)
p;成功確率（将棋；勝率＝P_0、サイコロ；１が出る確率）
４．棄却ルールを決める
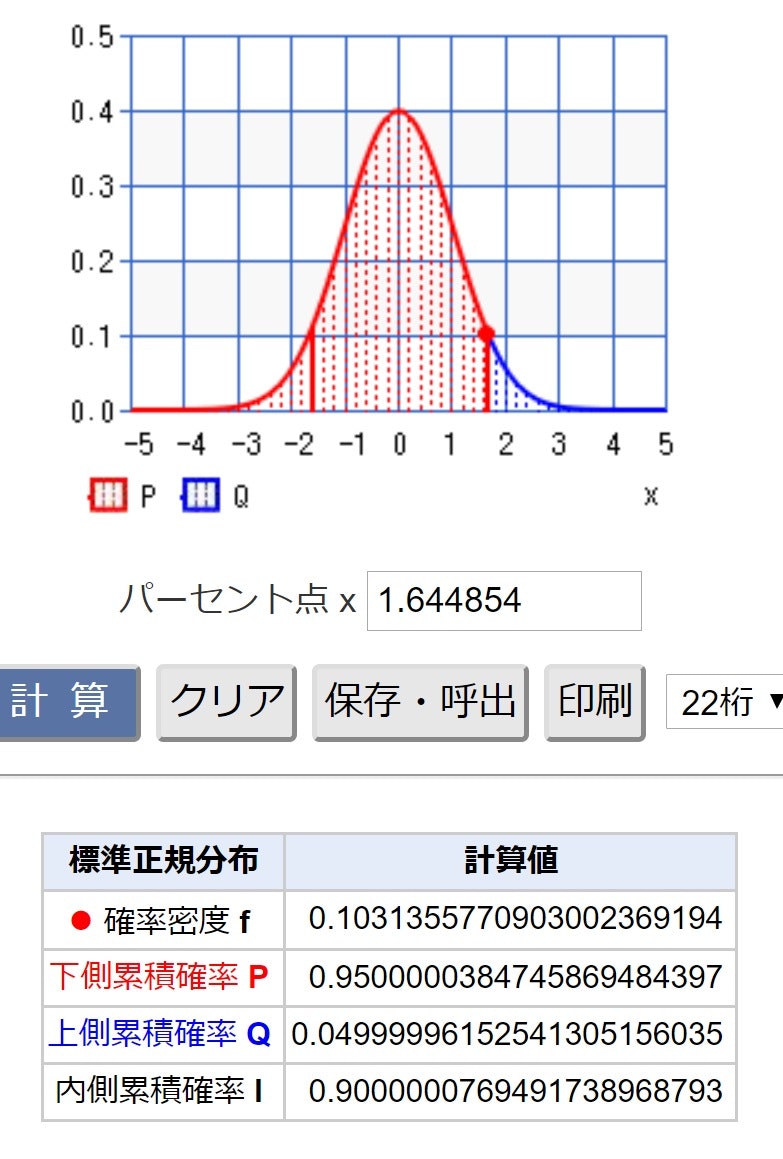
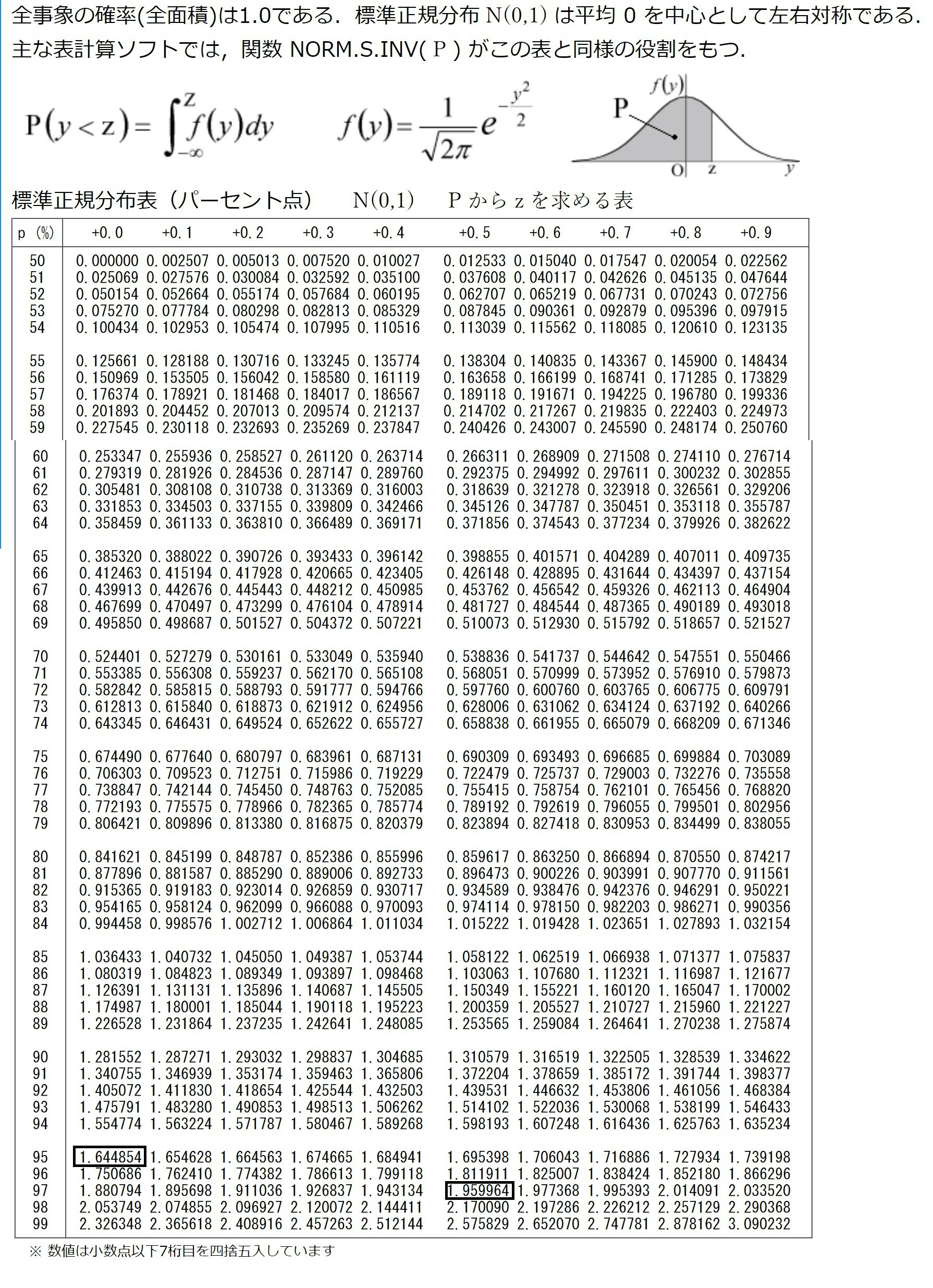
将棋；統計数値表（おまけ）からZ_0.05の値を読み取ると「1.644854」
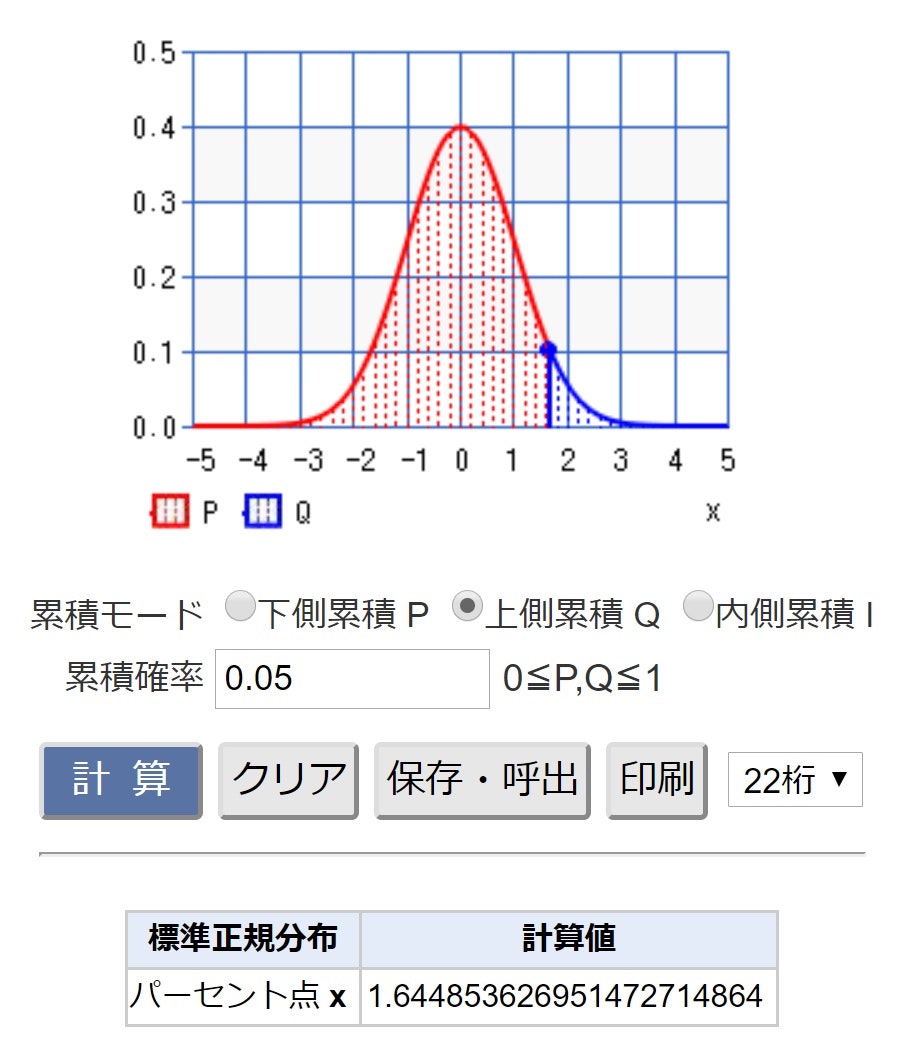
サイコロ；両側検定で、統計数値表（おまけ）からZ_0.025の値を読み取ると「1.96」
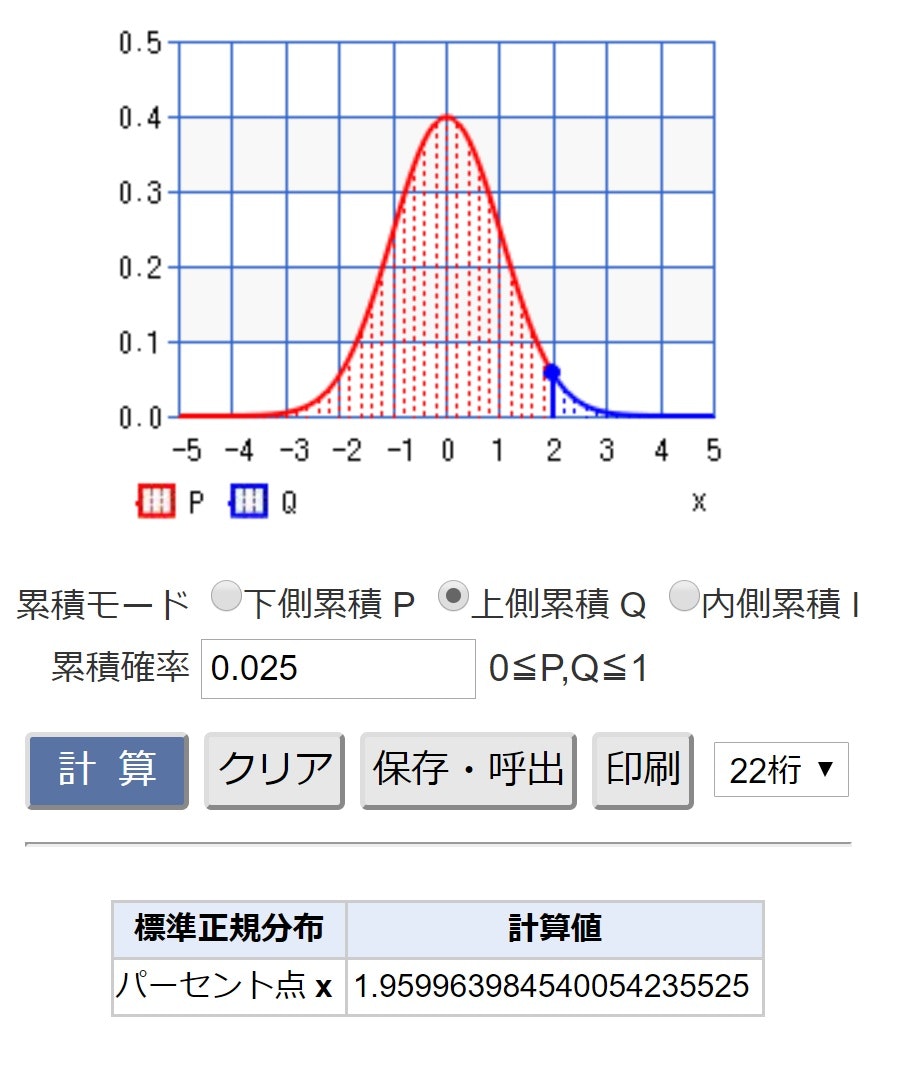
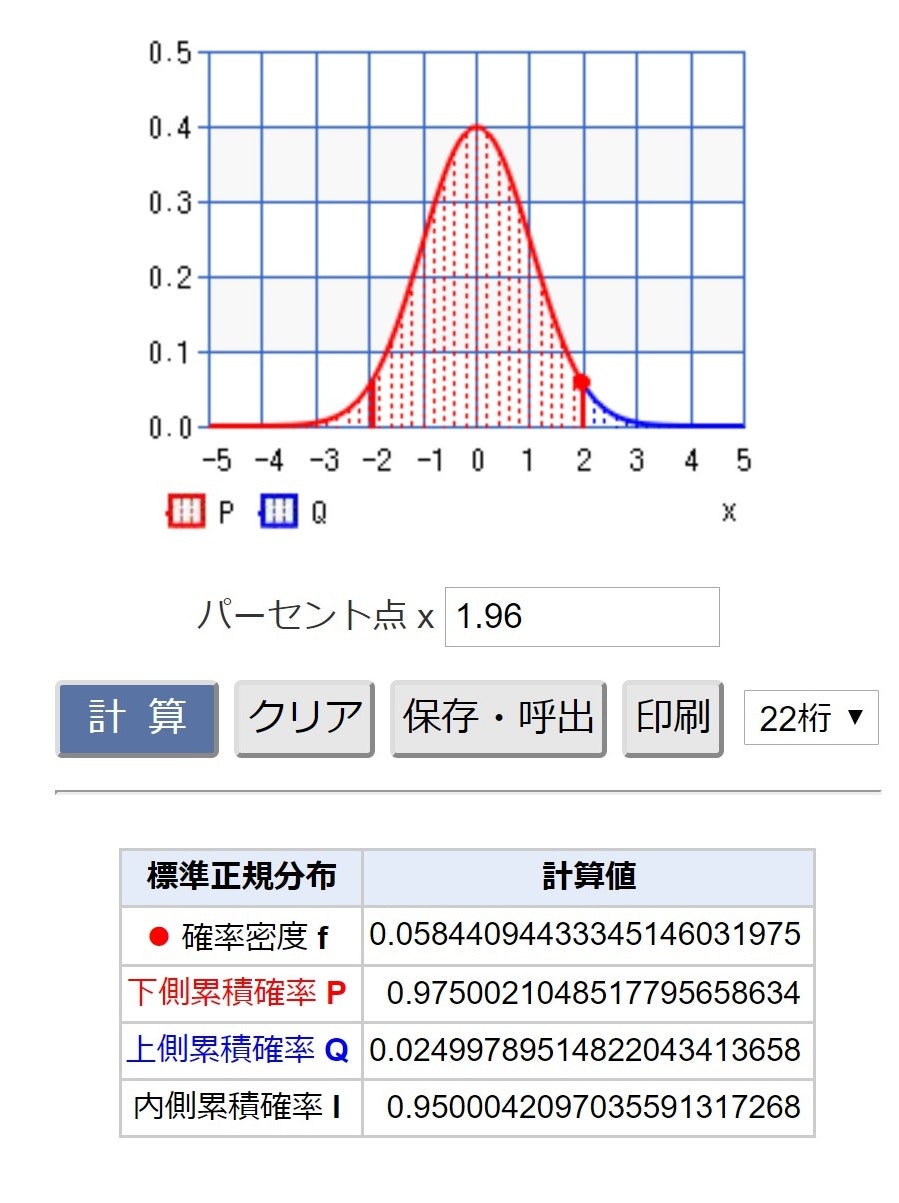
【参考】以下の参考サイトで計算しました
・標準正規分布@CASIO
・標準正規分布（パーセント点）
５．検定統計量を元に結論を出す
将棋；X=38回、n=50回（正確には４９とすべきだが）、p=0.5
z=\frac{38/50-0.5}{\sqrt{0.5(1-0.5)/50}}=\frac{0.26}{0.07071}\fallingdotseq 3.68
このｚは、上図のｘに対応する量なので、上図でz=3.68を見ると、もともとの仮説した値のはるか上なので、仮説棄却域にあり、優位に強いと云える。
サイコロ；X=2200,n=12,000,p=1/6
z=\frac{2200-2000}{\sqrt{2000(1-1/6)}}\fallingdotseq 4.899
こちらも同じで4.899はやはりはるか上なので仮説棄却域にあり、ばらつきがないとは言えないので、1／6の確率で出るとは言えないという結論が得られる。
###まとめ
・５０回対戦してやはりLesserKaiを打倒した
・二項分布を標準正規分布に規格化して、有意水準を設定し、帰無仮説を棄却し、有意に強いことを示した
###おまけ
標準正規分布表
