今回は、対数プロットすることにより各国の感染ピークの時期を予測することとする。
やったこと
・ちょっと理論
・各国の予測
・コード解説
・追加の理論
・各国の予測II
・ちょっと理論
前回、以下の式を導出した。
I = I_0\exp(\gamma (\frac{\beta}{\gamma} \frac{S}{N} - 1)t)\\
この両辺を対数取ると、
\ln I = \ln I_0+\gamma (\frac{\beta}{\gamma} \frac{S}{N} - 1)t\\
が得られる。すなわち、縦軸に$\ln I$横軸に時間$t$を取ったグラフを描くと、傾きが
\gamma (\frac{\beta}{\gamma} \frac{S}{N} - 1)\\
の直線が描ける。ここで、この傾きは$S$に依存しており時間と共に減少する未感染者数である。
そして、この傾きは前回導入した実効再生産数$R$を使うと以下のように書き換えられる。
\gamma (R - 1)\\
R = R_0 \frac{S}{N}\\
R_0 = \frac{\beta}{\gamma}\\
したがって、この傾きはR=1で0になり、すなわち再生産数=0となり、これ以上感染者が増えないので感染ピークとなる。
今回は、この理論を根拠に各国のデータを$\log I\ vs\ t$でプロットし、それぞれの国の感染ピークの時期を見たいと思う。
また、あわよくば立ち上がりの傾きから、$S\fallingdotseq N$であり、$\gamma (R_0 -1)$が得られる。
これを初期値にして得られたグラフをフィッティングすると、$\gamma$,$\beta$,$R_0$が求められそうである。
・各国の予測
・Korea, South, Diamond Princess, Italyの状況
Italyが入っているのが不信に思われるかもしれませんが、結果は以下のとおりです。
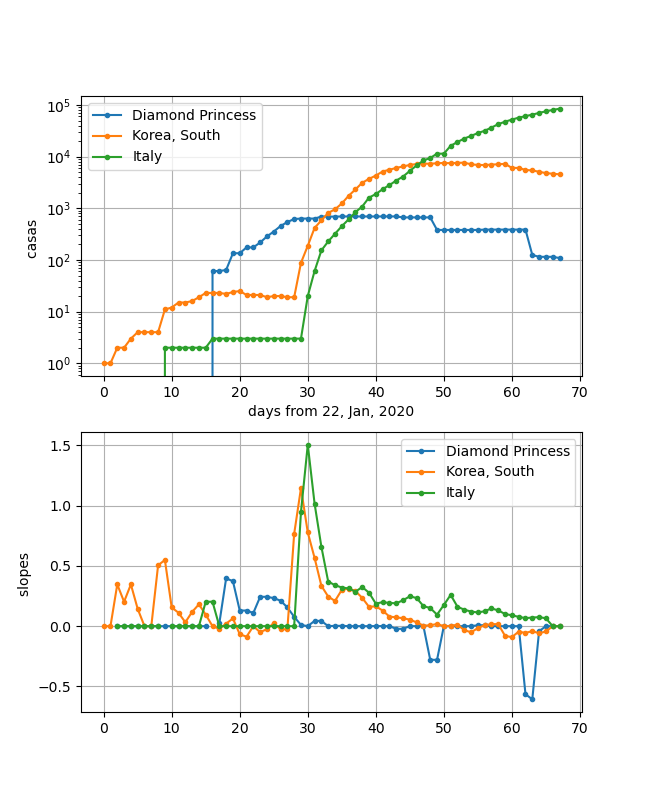
この3つの国を並べてみると、割と様になっているのが分かります。
すなわち、適当にx,y軸を平行移動すると重なりそうです。つまり、傾きが同一な領域があることが分かります。
どのグラフも、ほぼ10日で10倍になる区間が見えます。
そうです、DPが最初に感染数曲線が飽和し、次に韓国、そしてこれからイタリアがまさしく飽和しそうな状況です。下のグラフは傾きをプロットしています。すなわち、0になると飽和したことを表します。
ということで、このグラフからも上記のことが分かります。
イタリアに関して言及すると、いろいろ言われてきましたがあと10日程度でピークに達すると思われます。
・ヨーロッパ各国の状況
イタリア以外の、Spain,Germany,Switzerland,United Kingdom, Netherlandsについて、同一のグラフで表示します。
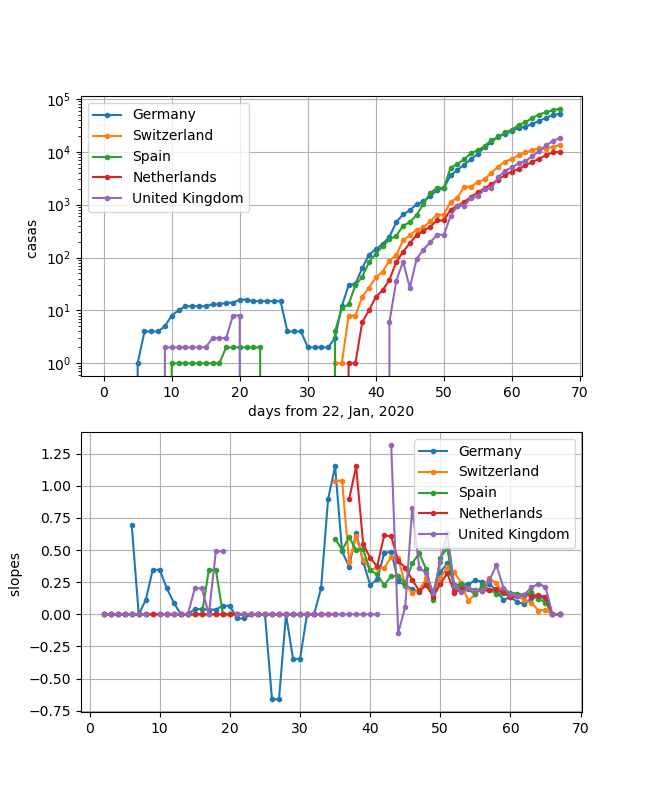
重ねて書いてみると、イギリスが少し遅れていますが、その他はよく似ている曲線を描いています。
縦軸はそれぞれの事情に依存して(人口など)異なりますが、ほぼ同様な傾きの変化をしています。
そして、傾きの図を見ると2週間程度内にはまとめて飽和してきそうです。
・ちょっと残念な国
Japan, Iran, Bahrainの3つの国もある意味曲線が酷似しています。
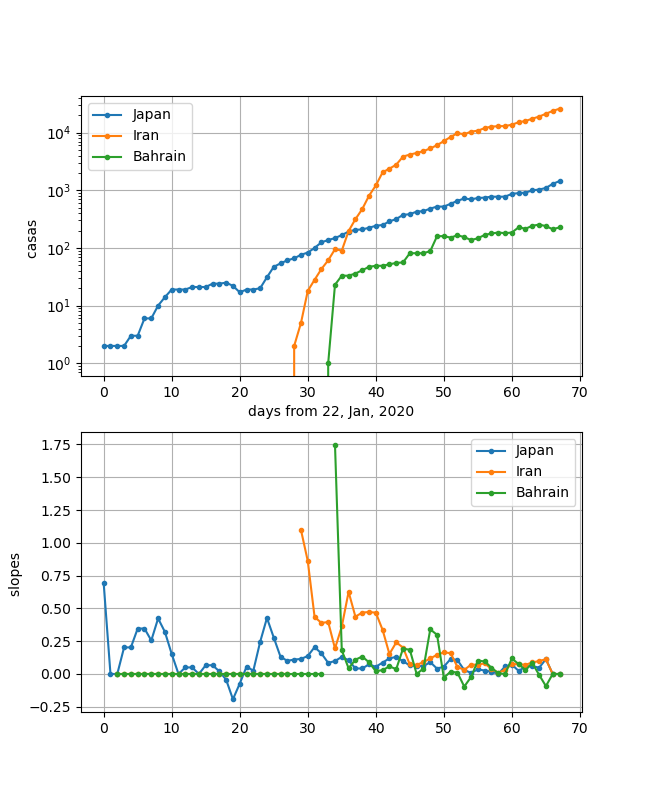
立ち上がりの状況が異なるので、y軸が全く違うので医療体制の状況は異なると思います。
しかし、一旦立ち上がってしまったあとの傾きが割と似ており、しかもこの何日間でほぼ飽和しているにも関わらず、イランと日本は再度スーと増加してしまっています。バーレーンも傾きが負になっているのですが、再度正に戻ってしまっています。
これら3国の勾配は、安定してからの勾配として10倍/30日程度のいつでも飽和しそうな緩い勾配になっています。
これらの国はまだまだ感染が継続しており、緊張を持って社会全体で封じ込めて行く必要があります。
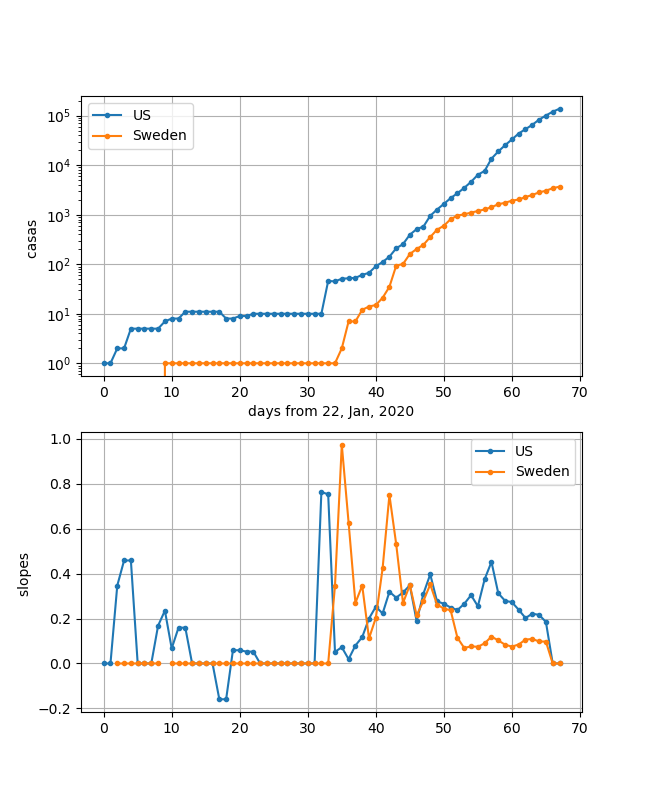
・噂のアメリカの状況
一目瞭然ですが、立ち上がりは似ています。しかし、スウェーデンは途中から傾きが小さくなっています。しかし、下の傾きのグラフを見るとこのところほぼx軸に平行になっていて、0に向かっているようには見えません。つまり、近日中に飽和はしないように見えます。
ただしアメリカは、58日から65日のデータがそろってきていて、傾きが0に向かって急激に近づいているようにも見えます。これを伸ばすとあと10日程度で感染ピークになる可能性もあることが分かります。
なお、両国の最大勾配は25倍/20日程度で先ほどの勾配より大きいのが分かります。
・コード解説
利用するLibとデータ読み込みは前回と同一です。
死亡数データも処理していますが、以下では使わないので削除しています。
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import pandas as pd
# pandasでCSVデータ読む。
data = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv')
data_r = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv')
以下、データ加工関数で、処理した感染数データと勾配データを返します。
def data_city(city):
#データを加工する
t_cases = 0
t_recover = 0
t_deaths = 0
for i in range(0, len(data_r), 1):
if (data_r.iloc[i][1] == city): #for country/region
#if (data_r.iloc[i][0] == city): #for province:/state
print(str(data_r.iloc[i][0]) + " of " + data_r.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed_r[day - 4] += data_r.iloc[i][day]
t_recover += data_r.iloc[i][day]
for i in range(0, len(data), 1):
if (data.iloc[i][1] == city): #for country/region
#if (data.iloc[i][0] == city): #for province:/state
print(str(data.iloc[i][0]) + " of " + data.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed[day - 4] += data.iloc[i][day] - confirmed_r[day - 4]
diff_confirmed[day - 4] += confirmed[day-4] / confirmed_r[day - 4]
tl_confirmed = 0
dlog_confirmed = [0] * (len(data.columns) - 4)
dlog_confirmed[0]=np.log(confirmed[0])
dlog_confirmed[1]=np.log(confirmed[1])-np.log(confirmed[0])
for i in range(2, len(confirmed)-2, 1):
if confirmed[i] > 0:
dlog_confirmed[i]=(np.log(confirmed[i+1])-np.log(confirmed[i-1]))/2
else:
continue
tl_confirmed = confirmed[len(confirmed)-1] + confirmed_r[len(confirmed)-1] + confirmed_d[len(confirmed)-1]
t_cases = tl_confirmed
return confirmed, dlog_confirmed
複数の国を同一図上にプロットするために以下のようにしています。
city_listに描きたい国を入れます。
上記のデータ処理関数で感染数データとその片対数の傾きを取得します。
これを描画します。
そのためにfig, (ax1,ax2) = ...の定義をfor文外で定義しました。
最後にまとめて、表示します。
colorはあえて定義せず、自動で選んでもらっています。
city_list={ "Spain","Germany","Switzerland","United Kingdom", "Netherlands" }
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(1.6180 * 4, 4*2))
for city in city_list:
confirmed = [0] * (len(data.columns) - 4)
confirmed_r = [0] * (len(data_r.columns) - 4)
confirmed_d = [0] * (len(data_d.columns) - 4)
diff_confirmed = [0] * (len(data.columns) - 4)
days_from_22_Jan_20 = np.arange(0, len(data.columns) - 4, 1)
days_from_22_Jan_20_ = np.arange(0, len(data.columns) - 4, 1)
recovered_rate = [0] * (len(data_r.columns) - 4)
deaths_rate = [0] * (len(data_d.columns) - 4)
confirmed, dlog_confirmed = data_city(city)
#matplotlib描画
lns1=ax1.semilogy(days_from_22_Jan_20, confirmed, ".-", label = str(city))
lns4=ax2.plot(days_from_22_Jan_20_, dlog_confirmed, ".-",label = str(city))
ax1.set_xlabel("days from 22, Jan, 2020")
ax1.set_ylabel("casas ")
ax2.set_ylabel("slopes ")
ax1.legend(loc=0)
ax2.legend(loc=0)
ax1.grid()
ax2.grid()
plt.pause(1)
plt.savefig('./fig/logmulti_{}_.png'.format(city))
plt.close()
・追加の理論
実は、治癒数曲線の推移は回復に遅れはあるが、感染数曲線と類似しているだろうという想像ができる。
ということで、以下その話を眉唾だがやってみた。
まず、SIRモデルの第三方程式に$I$を代入すると以下のとおりとなる。
※再生産数のRと回復数のRが被るのでここでは回復数を小文字にした
\frac{dr}{dt} = \gamma I_0\exp(\gamma (R - 1)t) \\
従って、両辺の対数を取ると
\ln (\frac{dr}{dt}) = \ln \gamma + \ln I_0 + \gamma (R - 1)t \\
となる。すなわち、回復率の時間微分(傾き)は上式と傾きが同じ曲線になることが期待でき、y切片が$\ln \gamma$だけ異なるものが得られる。
しかし、これだと誤差も大きく扱い難そうなので、ちょっと変更します。
すなわち、(解析的には正しくないが)Rがコンスタントとして積分すると以下の式を得る。
r = \frac{I_0}{(R-1)}\exp(\gamma (R - 1)t) + r_0\\
したがって、両辺対数取ると
\ln r = \ln I_0 -\ln (R-1) + \gamma (R - 1)t +\ln r_0
と書ける。ということで上記の$\ln I$の式と比較するとほぼ平行でy切片が$-ln (R-1)+\ln r_0$異なる曲線が得られることが期待できる。
・各国の予測II
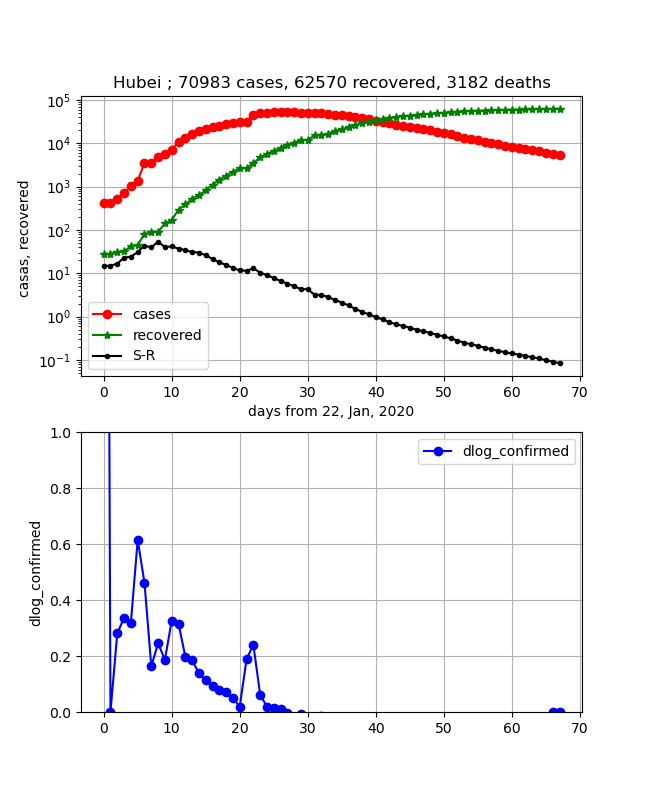
・武漢の状況
以下のように綺麗な曲線が得られました。予想どおり感染数曲線と治癒数曲線は平行に始まり感染数ピークを過ぎたところで交差します。
それに合わせて、二つの曲線の差分($\log (A/B)=\log A-\log B$)は直線的に$10^0$を通過します。
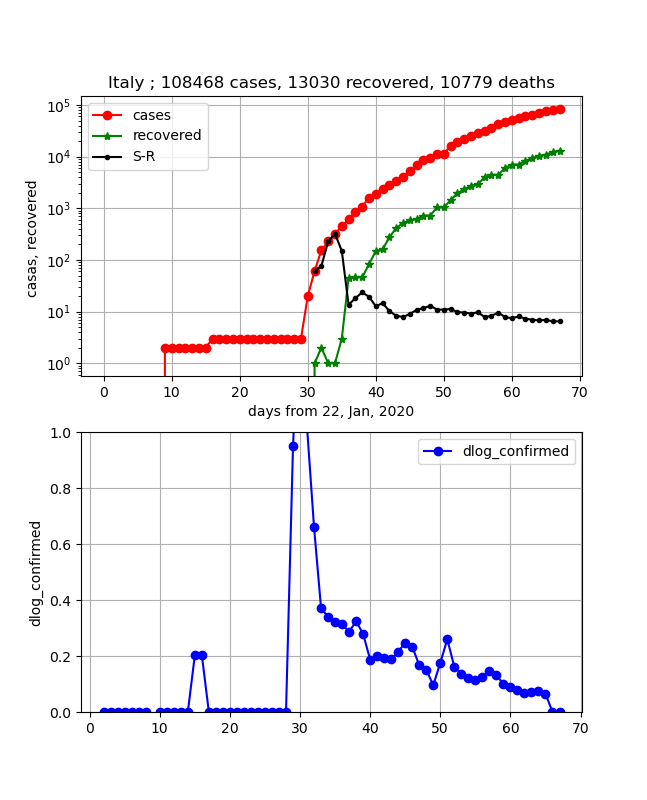
・イタリアの状況
両曲線が平行になっており、上では10日程度で感染数ピークになりそうという結論を出しましたが、そのあと、なかなか交差しないように見えます。
このあと、きっと近づいてきて交差するものと考察されますが、治癒数データが怪しいかもしれません。
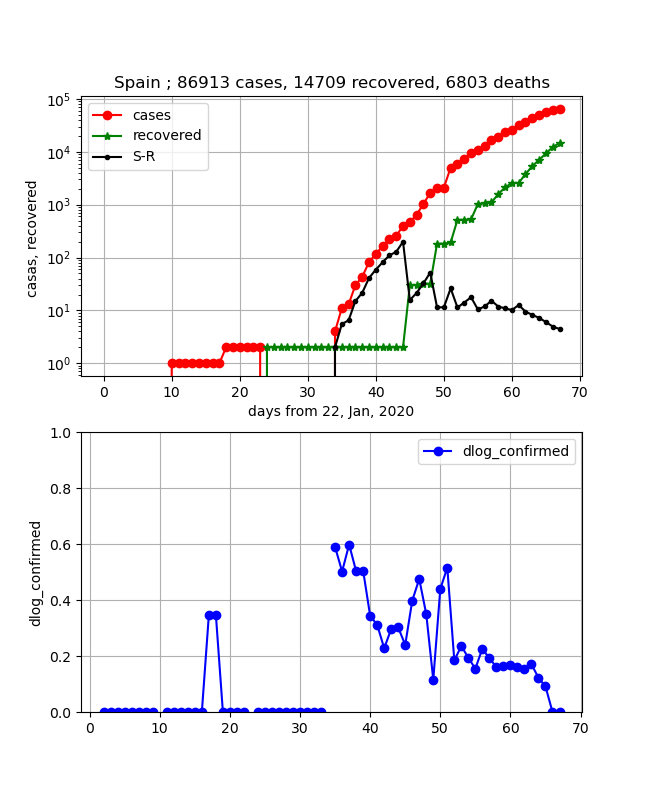
・ヨーロッパを代表してスペインの状況
着実に両曲線が近づきつつあり、感染数ピークのあと交差し終息が見えてくる状況です。
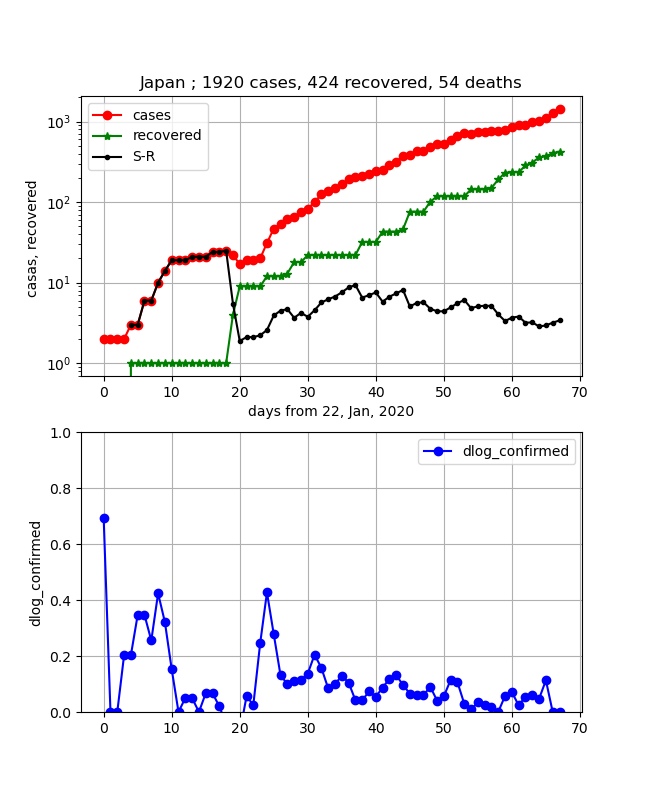
・日本の状況
日本はだんだん二つの曲線が近づいて来て、差は0に向かっていましたが、このところの感染数増加で差が広がってしまいました。ということで上記と同様、感染拡大は継続しているので抑え込みが必要という結論になります。
まとめ
・各国の感染数データを対数プロットして分類し、それぞれの感染数ピークの時期を予測した
・感染数と治癒数データを同時にプロットすることにより、終息時期を予測した
・日々変わる状況を追尾したいと思う
・追加部分の理論が怪しいのでもう少し整理し、パラメータ決定につなげようと思う