【Unity】カオスな連成振り子～リアルなモデルで薔薇が描けた♬

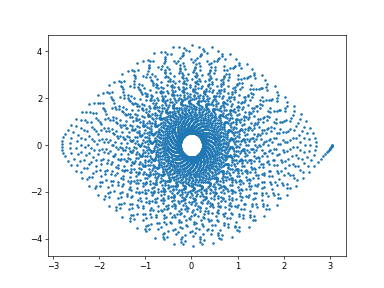
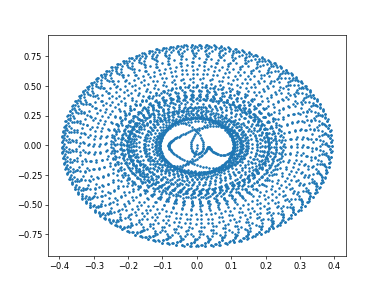
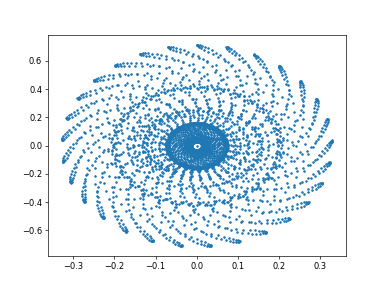
前回は天使が出てきたが、今回はバラが描けた。。。

やったこと

（１）バラが描けた～アートとして。。鑑賞♪
（２）モデルとコード
（３）OculusGoで見る

（１）バラが描けた～アートとして。。鑑賞

（２）モデルとコード

連成振り子の一番簡単なモデルは以下の参考のようにひもなどで連結したものである。
・連成振り子による非線形な振る舞いとカオス

m_1l_1\frac{dω_1}{dt} = -m_1g\sin(\theta_1) - k\theta_{21}{}

m_2l_2\frac{dω_2}{dt} = -m_2g\sin(\theta_2) + k\theta_{21}{}

この連立微分方程式をodeintするとパラメータによって上記のような絵が描ける。
コード例の主要な部分は以下のとおり

def dualPendulum(y, t, b, c):
    theta1, omega1,theta2, omega2 = y
    #theta21=theta2-theta1
    dydt = [omega1, -b*omega1 - c*np.sin(theta1)-0.06*(theta2-theta1),omega2, -b*omega2 - c*np.sin(theta2)+0.06*(theta2-theta1)]
    return dydt

b = 0.001  
c = 5.0
y0 = [np.pi - 0.1, 0.0,0, 0.0]
t = np.linspace(0, 10000, 4001)
sol = odeint(dualPendulum, y0, t, args=(b, c))
x1, p1,x2,p2 = sol.T[0], sol.T[1], sol.T[2], sol.T[3]

（３）OculusGoで見る

今回のポイントは、比較的簡単な相互作用であり、Unityでも同じような相互作用をすると想定できるので、同じような条件で降らせるとひょっとするとカオスが見られるかもしれない。。。

上記の描画を見ていると、比較的初期のころエネルギーをもらう側の振幅が小さいときにカオス的な振動が見られることが分かりました。
たとえば、以下のような振動の様子が観察されます。

この振幅が小さい部分を拡大すると以下のような振動になっています。
※パラメータは少し異なりますが。。
そして、この振幅の小さい側の振動は以前のカオスな振動の様子とよく似ていることが分かります。

ということでやってみました。
結果は、以下のような動画が得られました。

【OculusGo】リアルな連成振り子でカオスな運動をキャッチした♪
<img src="http://img.youtube.com/vi/zEHLSyKcrAg/0.jpg"

※画像をクリックするとYouTube動画につながります

一応、上記動画では、止まっていた振り子が引きずられように触れ始めまた静止して動き始めるときが一番カオス的な振動に見えます。。。ってちょっと無理してますが、。。

まとめ

・簡単な連成振り子でカオスな振舞をすることを微分方程式で見た
・位相空間の運動がまるで薔薇のような描画など多彩な描画ができた
・OculusGoでカオスな運動をVRできたと思う

・まだまだクリアな状況までの観察ができていない
・Flaskで計算した結果を渡すのも試みたが、初期動作が安定せず失敗したので実現したい