今回、この技法が注目されて以下のようなケースで使われるということで調べてやってみました。
1.画像データであらあらなデータしかないときに補間してくれる
2.そもそも行列式の解が欲しいのに、行列が一部抜けがあって補間が必要
3.画像がノイズがのっていて、どうにかしてノイズの評価と除去をやりたい
。。。参考のように観測値が少なくとも束縛条件で補間に寄与するというとやはりそうなのかなぁ~
って、先日の暗視カメラの画像処理に使えるのでは??
という軽い気持ちでやってみました。
一応、結論書きますと、ほんとに単調でほんとにスパースな画像では効果あるという評価です。
一晩寝て改めて、再評価すると以下の結果は、「カラー画像においても精度よくノイズ・リダクションできている」ですね。
1.画像が隙間だらけな場合(下のSplit Bregman法参考①で使っている画像拝借させていただきました)
ボケもなく、綺麗に修復されている。(おおもとの画像と比べると色相はずれている)
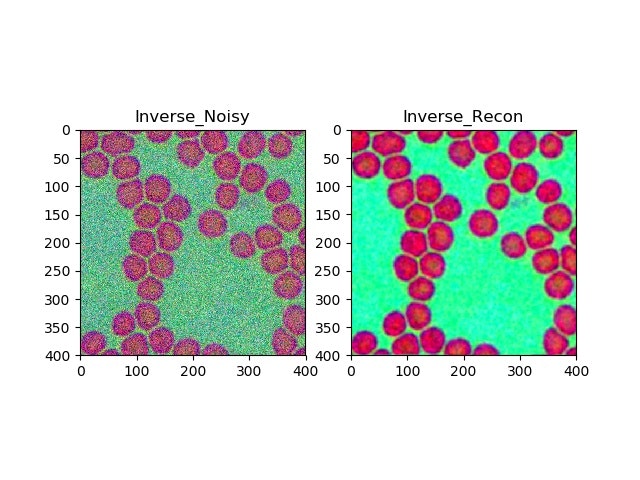
2.通常の画素値変動が密な画像(前回の花の絵)
若干ボケているけど、元画像(ノイズがのっている画像)のノイズが除去された。
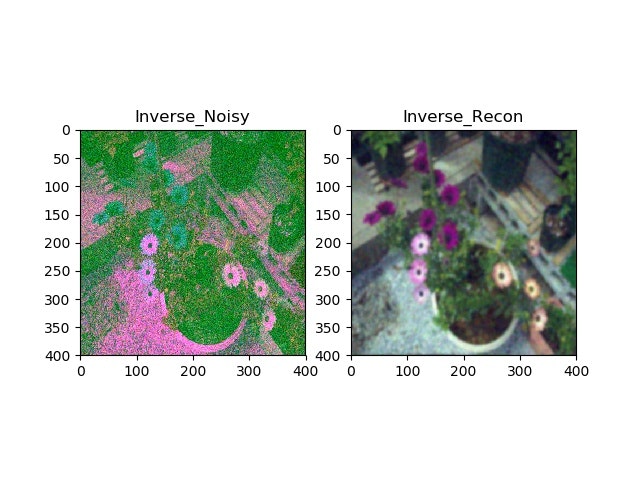
【参考】
・sparse modeling スパースモデリング
やったこと
・ラグランジュ未定係数法
・L1正則化による画像修復;スパース画像の修復
・Split Bregman法による画像修復
・カラー画像への適用
・結果の評価
・ラグランジュ未定係数法
これ基本です。
というか参考のとおりです。
【参考】
・ラグランジュの未定乗数法を実例で理解する
・ラグランジュの未定乗数法
ウワンは、以下の説明が分かりやすいです。
極値を求めたい式$f(x,y,z)$に対して、束縛条件$g(x,y,z)$がある場合、両者を満たすためには、新たな評価関数$F(x,y,z,\lambda)$を導入し、
F(x,y,z,λ)=f(x,y,z)−λg(x,y,z)
を作ります。ここで$\lambda$は適当な係数です。
この評価関数F(x,y,z,λ)に対して極値では少なくとも以下の式が同時に成り立つはずです。
つまり、この評価関数は変数空間$(x,y,z,\lambda)$において、どの方向においても極値になっていることが必要です。
\frac{∂F(x,y,z,λ)}{∂x}=0 \\
\frac{∂F(x,y,z,λ)}{∂y}=0 \\
\frac{∂F(x,y,z,λ)}{∂z}=0 \\
\frac{∂F(x,y,z,λ)}{∂λ}=0
そして、独立な束縛条件がある場合は、新たに$\lambda_1 g_1(x,y,z)$を導入し、$F(x,y,z,\lambda,\lambda_1)$を定義して同様な方程式群を解けばよいことになります。
参考①の最後の例題は,台形の4つの角度を多数回測定して、求めるというものです。
1.台形の内角の和=360度
2.対角の和=180度
という二つの束縛条件があるので、上式をまじめに計算すると、測定結果から各角度a,b,c,dを求めるのに以下のような連立方程式が成り立ちます。
\begin{eqnarray}
\left[
\begin{array}{cccccc}
10 & 0 & 0& 0 & -1& -1 \\
0 & 10 & 0& 0 & -1& -1 \\
0 & 0 & 10& 0 & -1& 0 \\
0 & 0 & 0& 10 & -1& 0 \\
1 & 1 & 1& 1 & 0& 0 \\
1 & 1 & 0& 0 & 0& 0 \\
\end{array}
\right]
\pmatrix{ a \\ b \\ c \\ d \\ \lambda_1 \\ \lambda_2 } = \pmatrix{ 2 \sum_{i=1}^{5}{a_i} \\ 2 \sum_{i=1}^{5}{b_i} \\ 2 \sum_{i=1}^{5}{c_i} \\ 2 \sum_{i=1}^{5}{d_i} \\ 360 \\ 180 }
\end{eqnarray}
以下のコードで解きました。つまり、scipyのライブラリを使っちゃいました。。
import numpy as np
import scipy.linalg as linalg
# initialize the matrix
A = np.array([[10.01, 0, 0, 0,-1.0001,-1.000001],
[0, 10.001, 0, 0,-1.0001,-1.000001],
[0, 0, 10.001, 0,-1.0001,0],
[0, 0, 0, 10.001,-1.0001,0],
[1.0001, 1.001, 1.0001, 1.00001,0,0],
[1.0001, 1.001, 0, 0,0,0]])
b = np.array([1399.74,400.54, 800.24, 1000.22, 360,180])
LU = linalg.lu_factor(A)
x = linalg.lu_solve(LU, b)
print(x)
ちなみに、あとで出てくるGauss_Seidel法やJacobi法ではSingular-Matrixのエラーが出て、解けませんでした。
【参考】
・Python NumPy サンプルコード: ヤコビ法
・Python NumPy サンプルコード: ガウス・ザイデル法
・L1正則化による画像修復;スパース画像の修復
これも参考のとおりです。参考を見ればそのままで行けると思いますが、コードが少し難しかったので分かったことを解説しておきます。※L1正則化がピンとこない場合はWikipediaを見るとわかると思います
【参考】
・正則化@wikipedia
・スパースモデリングに基づく画像の再構成 Part1. L1ノルム最小化に基づく画像再構成の実装
今回の評価関数は以下のとおりです。この関数をミニマムにする要素を求めます。ここで第一項は入力画像と出力画像が同じになるように働く二乗誤差です。第二項はいわゆるL1正則化項で、出力画像の要素をなるべく0になるように働きます。これが上記の未定係数法と同様で束縛条件に対応します。つまり、そのほかにも束縛条件がある場合は、未定係数をつけて条件として加えることができます。
F=\frac{1}{2}|I_{input}-I_{output}|^2 + \lambda|I_{output}|
GrayScaleの場合は、A=255として以下のような条件として書けます。
F=\frac{1}{2}|I_{input}-I_{output}|^2 + \lambda|I_{output}ーA|
画像の場合、上記の評価関数は以下のように記載できます。
F=\frac{1}{2}\sum_i(x_i-b_i)^2 + \lambda\sum_ix_i \\
\ =\frac{1}{2}\sum_i(a_i-b_i)^2 + \lambda\sum_ia_i \\
\ =\frac{1}{2}\sum_i(a_i-|b_i|+\lambda)^2 + 2\lambda|b_i|-\lambda^2
を最小化するには第一項が最小になればよい
a_i=max(|b_i|-\lambda,0)
ということで、コードの主要な部分は以下のとおりです。
LAMBDA = 30 ## 正則化パラメータ
THRE = 200 #np.round(np.mean(I)) #200 ## だいたい画素値200 くらいが background
print('THRE=',THRE)
B = I - THRE
t = np.sign(B)*B - LAMBDA
I_reconst = t*np.sign(B) + THRE #t*(t>0)*np.sign(B)
コードはもう一段工夫されていて、Iからバックグラウンドの値を引いてからイテレーションしています。なお、ここで(t>0)はTrueを返してるだけでした。
結果画像は以下のとおりになりました。

λを変更したときは以下のような画像が得られます。

一応、途中でノイズを載せていますが、適当なλを選べば消せているのが分かります。
しかし、この手法ではあまり精度は出せそうにありません。
・Split Bregman法による画像修復
【参考】
・①最適化方法: Split Bregman
・②A Review of the Split Bregman Method for L1 Regularized Problems
以下の評価関数を使います。
F=|d_x|+|d_y|+\frac{\lambda}{2}|u-I| \\
s.t. d_x=\nabla_xu,\ d_y=\nabla_yu
such thatの項は、いわゆる束縛条件として上式に追加します。
二乗で入れているので、より強い制限(L2正則化)として効いてくると思います。(参考は制約条件を少し弱め。。これは元々代入するのに比較してと読めます)ということで、未定係数$\lambda$, $\mu$として以下の評価関数Fを最小にするuを求めます。ちなみにこの式は、微係数0と入力画像に一致、そして上記の微分がd_x,d_yなどと一致することを要求します。
F=|d_x|+|d_y|+\frac{\lambda}{2}|u-I|+ \frac{\mu}{2}(|\nabla_xu-d_x|^2 +|\nabla_yu-d_y|^2)
そして、Bregman Iterationというのを導入して、以下のような漸化式に変形します。(※ここは参考②にあるけどきちんとは把握できていません)
※たぶん、$u^{k+1}=u^k+\nabla_xu^k+\nabla_yu^k$で、$b_x^k=\nabla_xu^k$,$b_y^k=\nabla_yu^k$
u^{k+1}=|d_x|+|d_y|+\frac{\lambda}{2}|u^k-I|+ \frac{\mu}{2}(|\nabla_xu^k-d_x-b_x^k|^2 +|\nabla_yu^k-d_y-b_y^k|^2)
上記の参考②では以下の画像が出ていました。まんま引用させていただきます。
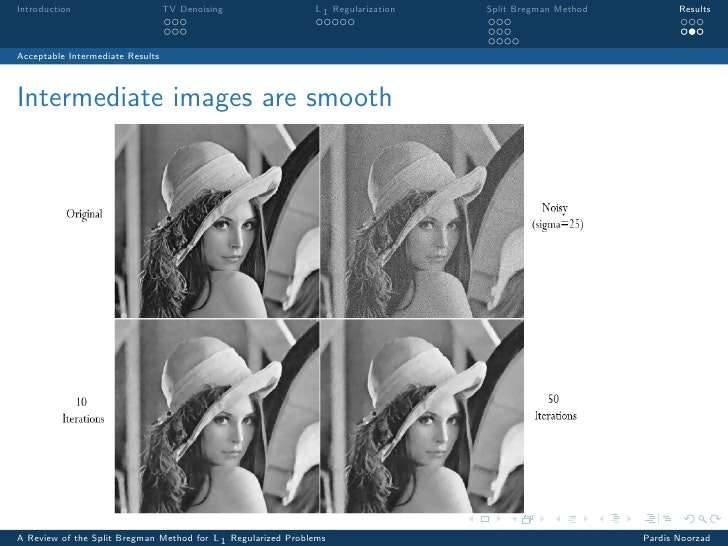
また、この参考①の記事では以下のような結果が掲載されています。

このGray画像では同様な絵が以下のおまけのコード(主要部分)で得られました。
※このコードは入力画像が別な箇所にあるので注意です。また、その画像はh=wでないとGauss_Saidel関数でエラーがでました。
・カラー画像への適用
一応、参考記事は白黒のガウシアンノイズの修復までやっていますが、やはり普通のカラー画像に適用したいということで、三色に分割してそれぞれを分離して修復して戻すということでカラーを実施しました。
その結果は以下のとおりです。
※例によってカラー空間は全てやってみましたが、まあ一様にほぼ同様な結果でした

結果は、いい感じにノイズは消えています。ただし、途中Normalizeしてしまっているので、カラーバランスが崩れてOriginalの色には帰りません。対応する画像を列に並べています。
※たぶん、Originalの画像に戻すことはできますが今回はやっていません
ところが、花の絵だと以下のような絵になっています。残念ながら、ノイズは消えますが、元画像よりは画像が劣化してぼやけています。
以下は、rgbのままノイズリダクションしています。

以下は、一度YCrCb空間に変換してからノイズリダクションして、再度元へ戻しています。やはり、画素の数値を変換してしまっているので、ぼけだけでなく色相も変化してしまいました。

結果の評価
1.画像が隙間だらけな場合
元画像(ノイズがのっている画像)
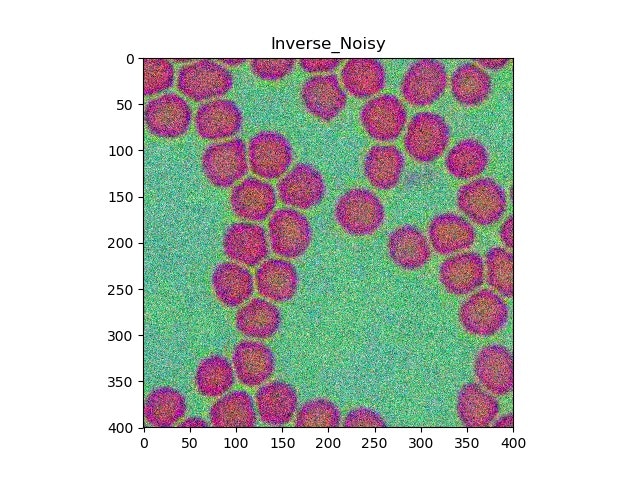
修復画像(ノイズが除去されている)
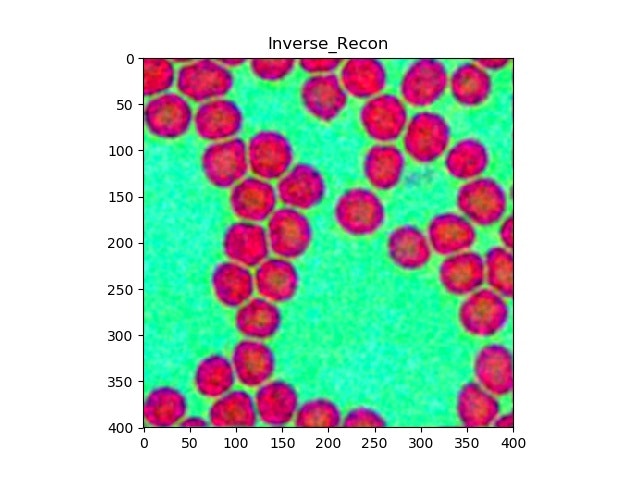
2.通常の画素値変動が密な画像(前回の花の絵);YUV空間に変換して実施
元画像(ノイズがのっている画像)
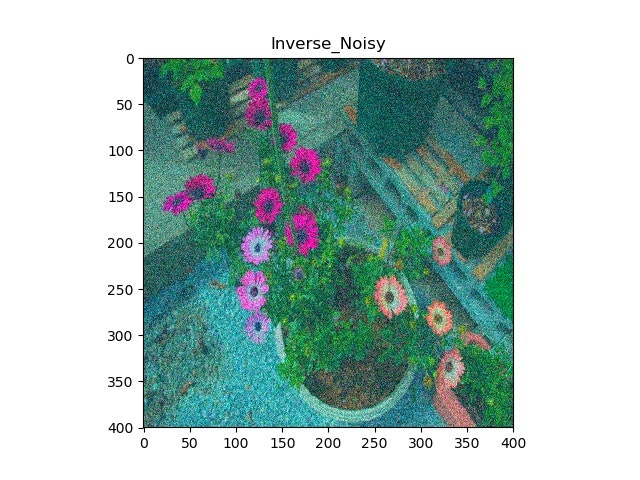
修復画像(少しボケているけど、色相もずれているが、ノイズは除去されている)
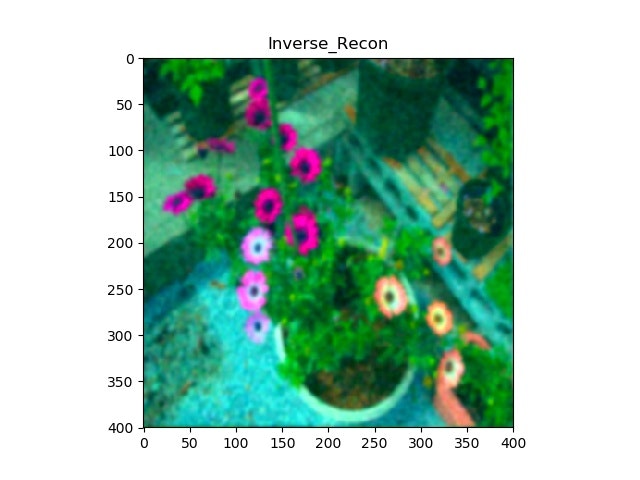
3.通常の画素値変動が密な画像(前回の花の絵);rgb空間のまま実施すると色相はずれていない
元画像(ノイズがのっている画像)
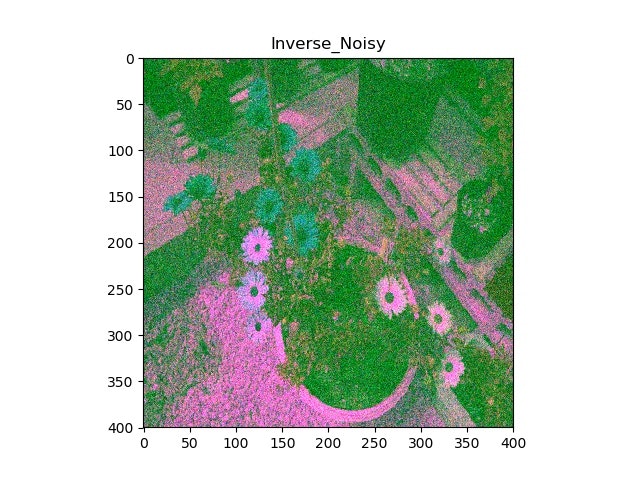
修復画像(少しボケているけど、ノイズが除去されており、色相のずれは目立たない)

評価
つまり、Gauss-Seidelにとっては、おおもと画像は知らず、ただ入力になっているノイズ画像をたよりに修復しているので、この結果(ノイズ除去)はスパース画像はもちろんだが、通常のカラー画像でもすごい精度なのだと再認識した。また、色相の変化は空間変換の画素値の規格化及び描画時にnp.clipで範囲指定していることが原因であり、ここは精緻にコードを直せば改善の余地はあると考えている。
ここは、今後の改善として残すこととする。
まとめ
・Sparse-Modelingでカラー画像のノイズ・リダクションを実施した
・ノイズ・リダクションはスパース画像はもちろんだが、通常画像も一定の精度でできた
・おおもとの画像に比較すると、ぼけが発生、空間を変換して実施したものでは色相のずれも目立つ
・ヒストグラム等により最適化を実施してカラー画像の鮮明化および星座写真等のダーク減算に挑戦しようと思う
・Split-Bregman以外の方法も開発されているらしいので、もう少し発展させようと思う
・単純に抜けのある画像のDLでの修復をやろうと思う
おまけ
"""
uk+1=minimize_u |dx|+|dy|+\frac{λ}{2}|u−I|^2+\frac{μ}{2}(|∇_xu−dx−b^k_x|^2+|∇_yu−dy−b^k_y|^2)
"""
import numpy as np
import cv2
import matplotlib.pyplot as plt
import random
def add_noise(I_t):
mu = np.mean(I_t)
sigma = np.std(I_t)
dB = 3
I_noise = 10**(-dB/20)*np.reshape([random.gauss(mu, sigma) for i in range(np.size(I_t))], np.shape(I_t))
print(np.max(I_noise), np.min(I_noise))
I = I_t + I_noise
max_I = np.max(I)
min_I = np.min(I)
I = (I - min_I)/(max_I - min_I)
return I
"""
u_{k+1}=minimize_u |d_x|+|d_y|+\frac{λ}{2}|u−I|^2+\frac{μ}{2}(|∇_xu−dx−b^k_x|^2+|∇_yu−dy−b^k_y|^2)
"""
def Gauss_Saidel(u, d_x, d_y, b_x, b_y, f, MU, LAMBDA,X_N,Y_N):
U = np.hstack([u[:,1:X_N], np.reshape(u[-1,:],[Y_N,1] )]) + np.hstack([np.reshape(u[0,:],[Y_N,1]), u[:,0:Y_N-1]]) \
+ np.vstack([u[1:X_N,:], np.reshape(u[:,-1],[1,X_N] )]) + np.vstack([np.reshape(u[:,0],[1,X_N] ), u[0:X_N-1,:]])
D = np.vstack([np.reshape(d_x[:,0],[1,X_N] ), d_x[0:Y_N-1,:]]) - d_x \
+ np.hstack([np.reshape(d_y[0,:],[Y_N,1] ), d_y[:,0:X_N-1]]) - d_y
B = -np.vstack([np.reshape(b_x[:,0],[1,X_N] ), b_x[0:Y_N-1,:]]) + b_x \
- np.hstack([np.reshape(b_y[0,:],[Y_N,1] ), b_y[:,0:X_N-1]]) + b_y
G = LAMBDA/(MU + 4*LAMBDA)*(U+D+B) + MU/(MU + 4*LAMBDA)*f
return G
def shrink(x,y):
t = np.abs(x) - y
S = np.sign(x)*(t > 0) * t
return S
def cycle_Gauss_Seidel(f,X_N,Y_N):
CYCLE = 10000 #1000 #300 #200 #100
MU = 0.05 #5 #5.0*10**(-2)
LAMBDA = 0.01 #0.1 #1 #1.0*10**(-2)
TOL = 1e-2 #3 #-1 #-5 #5.0*10**(-1)
X_N,Y_N=X_N,Y_N
## Initialization
u = f
d_x = np.zeros([X_N,Y_N])
d_y = np.zeros([X_N,Y_N])
b_x = np.zeros([X_N,Y_N])
b_y = np.zeros([X_N,Y_N])
for cyc in range(CYCLE):
u_n = Gauss_Saidel(u,d_x,d_y, b_x ,b_y,f, MU,LAMBDA,X_N,Y_N)
Err = np.max(np.abs(u_n[2:X_N-2,2:Y_N-2] - u[2:X_N-2,2:Y_N-2]))
if np.mod(cyc,200)==0:
print([cyc,Err])
if Err < TOL:
break
else:
u = u_n
nablax_u = np.vstack([u[1:X_N,:], np.reshape(u[:,-1],[1,X_N] )]) - u
nablay_u = np.hstack([u[:,1:X_N], np.reshape(u[-1,:],[Y_N,1] )]) - u
d_x = shrink(nablax_u + b_x, 1/LAMBDA)
d_y = shrink(nablay_u + b_y, 1/LAMBDA)
b_x = b_x + (nablax_u - d_x)
b_y = b_y + (nablay_u - d_y)
return u
def plot_fig(img='img_load',fig_name='default'):
plt.imshow(img)
plt.title(fig_name)
plt.savefig('Original_'+str(fig_name)+'.jpg')
plt.pause(1)
plt.close()
def main():
img_rows, img_cols = 400,400
img_path = "s7.jpg" #"s7.jpg" #"Blood2.jpg"
img_load = cv2.imread(img_path)
img_load = cv2.resize(img_load, (img_rows, img_cols), interpolation=cv2.INTER_CUBIC)
img_load = img_load[:,:,::-1]
plot_fig(img_load,'input')
img_load_o=img_load
r_o, g_o, b_o = cv2.split(img_load_o)
r_no=(r_o-np.min(r_o)) /(np.max(r_o)-np.min(r_o))
g_no=(g_o-np.min(g_o)) /(np.max(g_o)-np.min(g_o))
b_no=(b_o-np.min(b_o)) /(np.max(b_o)-np.min(b_o))
rgb_str= img_path+'YCrCb_2' #'YCrCb_5' #'rgb_5' #'rgb_2' #'LAB' #'YUV' #'HSV' #'YCR_CB' #'rgb'
img_load = cv2.cvtColor(img_load, cv2.COLOR_BGR2YCrCb)
#img_load = cv2.cvtColor(img_load, cv2.COLOR_BGR2HSV)
#img_load = cv2.cvtColor(img_load, cv2.COLOR_BGR2YUV)
#img_load = cv2.cvtColor(img_load, cv2.COLOR_BGR2LAB)
r, g, b = cv2.split(img_load) #cv2.cvtColor(img_load, cv2.COLOR_RGB2GRAY)
r_nco=(r-np.min(r)) /(np.max(r)-np.min(r))
g_nco=(g-np.min(g)) /(np.max(g)-np.min(g))
b_nco=(b-np.min(b)) /(np.max(b)-np.min(b))
plt.figure()
plt.subplot(321)
plt.axis("off")
plt.imshow(img_load_o)
plt.title("Original")
img_load_on = cv2.merge((r_no,g_no,b_no))
plt.subplot(322)
plt.axis("off")
plt.imshow(img_load_on)
plt.title("Original_norm")
plt.subplot(323)
plt.axis("off")
plt.imshow(img_load)
plt.title("Converted")
img_load_ic = cv2.merge((r_nco,g_nco,b_nco))
plt.subplot(324)
plt.axis("off")
plt.imshow(img_load_ic)
plt.title("Convd_norm")
img_load_c = cv2.cvtColor(img_load, cv2.COLOR_YCrCb2BGR)
#img_load_c = cv2.cvtColor(img_load, cv2.COLOR_LAB2BGR)
#img_load_c = cv2.cvtColor(img_load, cv2.COLOR_YUV2BGR)
#img_load_c = cv2.cvtColor(img_load, cv2.COLOR_HSV2BGR)
plt.subplot(325)
plt.axis("off")
#plt.imshow(img_load_c)
plt.title("Inversed")
img_load_ic = np.array(img_load_ic, dtype=np.float32) #np.float32) #np.uint8)
img_load_ic = cv2.cvtColor(np.clip(img_load_ic, 0, 1), cv2.COLOR_YCrCb2BGR)
#img_load_ic = cv2.cvtColor(img_load_ic, cv2.COLOR_LAB2BGR)
#img_load_ic = cv2.cvtColor(img_load_ic, cv2.COLOR_YUV2BGR)
#img_load_ic = cv2.cvtColor(img_load_ic, cv2.COLOR_HSV2BGR)
plt.subplot(326)
plt.axis("off")
plt.imshow(np.clip(img_load_ic, 0, 1))
plt.title("Inverse_norm")
plt.savefig('Original_Converted_normalized_'+rgb_str+'_.jpg')
plt.pause(1)
plt.close()
list=(r,g,b)
s=0
rgb=[]
rgbs=[]
for I_t in list:
plot_fig(I_t,'Original'+rgb_str+str(s))
f = add_noise(I_t) #I_t #add_noise(I_t)
plot_fig(f,'Noise_'+rgb_str+'_'+str(s))
[X_N,Y_N] = np.shape(f)
print(X_N,Y_N)
u = cycle_Gauss_Seidel(f,X_N,Y_N)
#u=f
## plot figure
plt.figure()
plt.subplot(1,3,1)
plt.axis("off")
plt.imshow(I_t)
plt.title("Original")
plt.subplot(1,3,2)
plt.axis("off")
plt.imshow(f)
plt.title("Noisy")
plt.subplot(1,3,3)
plt.axis("off")
plt.imshow(u)
#x1, y1 = [0,X_N], [X_N,Y_N] #[50,50]
#plt.plot(x1, y1)
plt.title('Reconstructed')
plt.savefig('Reconstructed_'+rgb_str+'_'+str(s)+'.jpg')
plt.close()
plt.figure()
plt.subplot(2,1,1)
plt.plot(f[50,:])
plt.subplot(2,1,2)
plt.plot(u[50,:])
plt.savefig('Tracing_'+rgb_str+'_'+str(s)+'.jpg')
plt.pause(1)
plt.close()
if s==0:
r=(u-np.min(u)) /(np.max(u)-np.min(u)) #/255
f_0=f
elif s==1:
g=(u-np.min(u)) /(np.max(u)-np.min(u)) #/255
f_1=f
else:
b=(u-np.min(u)) /(np.max(u)-np.min(u)) #/255
f_2=f
s+=1
#plt.close()
rgbs = cv2.merge((r,g,b))
plt.imshow(rgbs)
plt.savefig('Reconstructed_total_'+rgb_str+'.jpg')
plt.pause(1)
plt.close()
plt.figure()
plt.subplot(341)
plt.axis("off")
plt.imshow(img_load_o)
plt.title("Original")
plt.subplot(342)
plt.axis("off")
plt.imshow(img_load)
plt.title("Converted")
img_load_ic = cv2.merge((r_nco,g_nco,b_nco))
plt.subplot(343)
plt.axis("off")
plt.imshow(img_load_ic)
plt.title("Convd_norm")
rgb_o=cv2.merge((r_no,g_no,b_no))
plt.subplot(344)
plt.axis("off")
plt.imshow(rgb_o)
plt.title("Normalized")
fs = cv2.merge((f_0,f_1,f_2))
plt.subplot(347)
plt.axis("off")
plt.imshow(f)
plt.title("Noisy_norm")
fs = np.array(fs, dtype=np.float32) #np.uint8)
f_inv = cv2.cvtColor(np.clip(fs, 0, 1), cv2.COLOR_YCrCb2BGR)
#f_inv = cv2.cvtColor(np.clip(fs, 0, 1), cv2.COLOR_LAB2BGR)
#f_inv = cv2.cvtColor(np.clip(fs, 0, 1), cv2.COLOR_YUV2BGR)
#f_inv = cv2.cvtColor(np.clip(fs, 0, 1), cv2.COLOR_HSV2BGR)
plt.subplot(348)
plt.axis("off")
plt.imshow(np.clip(f_inv, 0, 1))
plt.title("Inverse_Noisy")
plt.subplot(3,4,11)
plt.axis("off")
plt.imshow(rgbs)
plt.title('Reconstructed')
rgbs = np.array(rgbs, dtype=np.float32) #np.uint8)
rgbs = cv2.cvtColor(np.clip(rgbs, 0, 1), cv2.COLOR_YCrCb2BGR)
#rgbs = cv2.cvtColor(np.clip(rgbs, 0, 1), cv2.COLOR_LAB2BGR)
#rgbs = cv2.cvtColor(np.clip(rgbs, 0, 1), cv2.COLOR_YUV2BGR)
#rgbs = cv2.cvtColor(np.clip(rgbs, 0, 1), cv2.COLOR_HSV2BGR)
plt.subplot(3,4,12)
plt.axis("off")
plt.imshow(np.clip(rgbs, 0, 1))
plt.title("Inverse_Recon")
plt.savefig('Original_Noisy_Reconstructed_'+rgb_str+'_.jpg')
plt.pause(1)
plt.close()
if __name__ == "__main__":
main()
def Gauss_Saidel(u, d_x, d_y, b_x, b_y, f, MU, LAMBDA):
U = np.hstack([u[:,1:X_N], np.reshape(u[-1,:],[Y_N,1] )]) + np.hstack([np.reshape(u[0,:],[Y_N,1]), u[:,0:Y_N-1]]) \
+ np.vstack([u[1:X_N,:], np.reshape(u[:,-1],[1,X_N] )]) + np.vstack([np.reshape(u[:,0],[1,X_N] ), u[0:X_N-1,:]])
D = np.vstack([np.reshape(d_x[:,0],[1,X_N] ), d_x[0:Y_N-1,:]]) - d_x \
+ np.hstack([np.reshape(d_y[0,:],[Y_N,1] ), d_y[:,0:X_N-1]]) - d_y
B = -np.vstack([np.reshape(b_x[:,0],[1,X_N] ), b_x[0:Y_N-1,:]]) + b_x \
- np.hstack([np.reshape(b_y[0,:],[Y_N,1] ), b_y[:,0:X_N-1]]) + b_y
G = LAMBDA/(MU + 4*LAMBDA)*(U+D+B) + MU/(MU + 4*LAMBDA)*f
return G
def shrink(x,y):
t = np.abs(x) - y
S = np.sign(x)*(t > 0) * t
return S
def main():
CYCLE = 100
MU = 5.0*10**(-2)
LAMBDA = 1.0*10**(-2)
TOL = 5.0*10**(-1)
## Initialization
u = f
d_x = np.zeros([X_N,Y_N])
d_y = np.zeros([X_N,Y_N])
b_x = np.zeros([X_N,Y_N])
b_y = np.zeros([X_N,Y_N])
for cyc in range(CYCLE):
u_n = Gauss_Saidel(u,d_x,d_y, b_x ,b_y,f, MU,LAMBDA)
Err = np.max(np.abs(u_n[2:X_N-2,2:Y_N-2] - u[2:X_N-2,2:Y_N-2]))
if np.mod(cyc,10)==0:
print([cyc,Err])
if Err < TOL:
break
else:
u = u_n
nablax_u = np.vstack([u[1:X_N,:], np.reshape(u[:,-1],[1,X_N] )]) - u
nablay_u = np.hstack([u[:,1:X_N], np.reshape(u[-1,:],[Y_N,1] )]) - u
d_x = shrink(nablax_u + b_x, 1/LAMBDA)
d_y = shrink(nablay_u + b_y, 1/LAMBDA)
b_x = b_x + (nablax_u - d_x)
b_y = b_y + (nablay_u - d_y)