前回のSEIRモデルでは、得られたパラメータのうち、$lp \fallingdotseq 1e^{-23}$などの値が得られた。こういうときは、桁落ちやそもそも微分方程式が機能していない可能性もあるので、注意せよ。
ということで、今回はこの部分を変更して、一番簡単なモデルでフィッティングしようと思う。
やったこと
・ちょっと理論
・コード解説
・日本の終息
・各国の終息
・ちょっと議論
・ちょっと理論
SIRモデルは以下のシンプルな時間発展方程式である。
{\begin{align}
\frac{dS}{dt} &= -\beta \frac{SI}{N} \\
\frac{dI}{dt} &= \beta \frac{SI}{N} -\gamma I \\
\frac{dR}{dt} &= \gamma I \\
\end{align}
}
第一方程式は未感染者の減少は、感染者数と未感染者数に比例し、全体の対象人数に反比例するということで、その係数βが感染率であり、その割合で未感染者が減少する。
β/Nとして、一人当たりの感染率と考えることもできる。
第二方程式は、感染者の増加の式である。増加は未感染者からの流入と治癒者との差分である。
第三方程式は、感染者のうち、一定割合が治癒するという式であり、この係数γが除去率と呼ばれる治癒率である。
【参考】
・この感染は拡大か収束か:再生産数 R の物理的意味と決定
ここで、第二式は以下のように式変形できる。
\frac{dI}{dt} = \gamma (\frac{\beta}{\gamma} \frac{S}{N} - 1)I\\
すなわち、$S/N$がコンスタントと考えると、形式的に以下のような解が得られる。
※十分微小な時間内での時間発展ではと考えてもよい
I = I_0\exp(\gamma (\frac{\beta}{\gamma} \frac{S}{N} - 1)t)\\
感染立ち上がりにおいては、$S_0\fallingdotseq N$であり、その場合以下のような解が得られる
{\begin{align}
I &= I_0\exp(\gamma (R_0 - 1)t)\\
ここで\\
R_0 &= \frac{\beta}{\gamma}
\end{align}
}
ここで、$I$の式は$R_0<1$の場合は感染者数は指数的に減少し、逆に$R_0>1$の場合は指数関数的に増加する。
したがって、この**$R_0$は基本再生産数**と呼ばれ、感染伝播が起こるかどうかを判断する目安となる。
さらに、上記の参考では、
R = R_0\frac{S}{N}
を実効再生産数と定義している。
この$R$は感染が進むと$\frac{S}{N}$が小さくなると小さくなる。すなわち上記の形式解を見れば分かるように、$R_0>1$のとき拡大初期においてもまだまだ$R>1$であり感染が拡大するが、いずれ$\frac{S}{N}$が小さくなり、$R<1$が実現すると終息が始まることを示す指標となる。
一方、$\frac{dI}{dt}=0$の左辺=0から感染ピークであり、このときの未感染者数を$S_p$とおくと、
{\begin{align}
R_0 &= \frac{\beta}{\gamma}\\
& = \frac{N}{S_p} \\
\end{align}
}
が成り立ち、このとき
{\begin{align}
R &= R_0\frac{S_p}{N}\\
&= 1
\end{align}
}
が成り立つことが分かる。すなわち、感染ピークで実効再生産数R=1であり、これ以降感染伝播は終息に向かう。
今回はこの実効再生産数もプロットすることにより終息予測を見てみようと思う。
・コード解説
コード全体は以下に置いた。
・collective_particles/fitting_SIR_COVID2.py
利用Libは以下のとおり、前回と同様です。
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import pandas as pd
COVID-19のサイトから予めデータをダウンロードしています。
# pandasでCSVデータ読む。
data = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv')
data_r = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv')
data_d = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv')
confirmed = [0] * (len(data.columns) - 4)
confirmed_r = [0] * (len(data_r.columns) - 4)
confirmed_d = [0] * (len(data_d.columns) - 4)
days_from_22_Jan_20 = np.arange(0, len(data.columns) - 4, 1)
データのレコード順が前回は正しく並んでいたが、今回は3つのデータの国や地域の順序が同じ順序ではないので、以下のようにそれぞれを取得し、かつ感染数データは現存感染数を計算するために治癒数データ取得後に取得するようにしています。
なお、if文は、それぞれ国と地方で入れ替えて使います。
また、死亡率と治癒率に必要な総治癒数と総死亡数は今回計算しないのでコメントアウトしています。
# City
city = "Japan"
# データを加工する
t_cases = 0
for i in range(0, len(data_r), 1):
if (data_r.iloc[i][1] == city): #for country/region
#if (data_r.iloc[i][0] == city): #for province:/state
print(str(data_r.iloc[i][0]) + " of " + data_r.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed_r[day - 4] += data_r.iloc[i][day]
#t_recover += data_r.iloc[i][day]
for i in range(0, len(data), 1):
if (data.iloc[i][1] == city): #for country/region
#if (data.iloc[i][0] == city): #for province:/state
print(str(data.iloc[i][0]) + " of " + data.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed[day - 4] += data.iloc[i][day] - confirmed_r[day - 4]
for i in range(0, len(data_d), 1):
if (data_d.iloc[i][1] == city): #for country/region
#if (data_d.iloc[i][0] == city): #for province:/state
print(str(data_d.iloc[i][0]) + " of " + data_d.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed_d[day - 4] += data_d.iloc[i][day] #fro drawings
#t_deaths += data_d.iloc[i][day]
今回はSIRモデルを利用します。
また、評価関数も未感染数S、感染数I、治癒数Rをすべて返値します。
# define differencial equation of sir model
def sir_eq(v,t,beta,gamma):
a = -beta*v[0]*v[1]
b = beta*v[0]*v[1] - gamma*v[1]
c = gamma*v[1]
return [a,b,c]
def estimate_i(ini_state,beta,gamma):
v=odeint(sir_eq,ini_state,t,args=(beta,gamma))
est=v[0:int(t_max/dt):int(1/dt)]
return est[:,0],est[:,1],est[:,2] #v0-S,v1-I,v2-R
目的関数は通常の分散としました。
ここでは感染数Iと治癒数Rを同時にフィッティング出来るように線形和にしました。
# define logscale likelihood function
def y(params):
est_i_0,est_i_1,est_i_2=estimate_i(ini_state,params[0],params[1])
return np.sum(f1*(est_i_1-obs_i_1)*(est_i_1-obs_i_1)+f2*(est_i_2-obs_i_2)*(est_i_2-obs_i_2))
上記で選択した国(または地方)にあった、総感染数をN0に入れます。
また、フィッティングをどの曲線についてやるかf1,f2で決定します。
N,S0,I0,R0はそれぞれの初期値ですが、これもフィッティングの具合で調整すべき定数です。
beta,gammaの初期値は、だいたいの国で同じような値ですが、一度得られた値を再度入れて回帰的に計算した方がよいようです。
※この初期値フィッティングするのもやるべきですが今回はやりません
# solve seir model
N0 = 1517
f1,f2 = 1,1 #data & data_r fitting factor
N,S0,I0,R0=int(N0*1.5),int(N0*1.5),int(10),int(0)
ini_state=[S0,I0,R0]
beta,gamma = 1.6e-6, 1e-3 #初期値はある程度近い値でないと収束しない
t_max=len(days_from_22_Jan_20) #データのある範囲でフィッティング
dt=0.01
t=np.arange(0,t_max,dt)
初期値確認含め、以下で一応表示してみます。
plt.plot(t,odeint(sir_eq,ini_state,t,args=(beta,gamma)))
plt.legend(['Susceptible','Infected','Recovered'])
obs_i_1 = confirmed
obs_i_2 = confirmed_r
plt.plot(obs_i_1,"o", color="red",label = "data_1")
plt.plot(obs_i_2,"o", color="green",label = "data_2")
plt.legend()
plt.pause(1)
plt.close()
フィッティングをします。今回もminimize@scipy使いました。
基本再生産数R0の計算をします。
変数名が上の治癒数初期値と被ったので小文字にしています。
# optimize logscale likelihood function
mnmz=minimize(y,[beta,gamma],method="nelder-mead")
print(mnmz)
# R0
# N_total = S_0+I_0+R_0
# R0 = N_total*beta_const *(1/gamma_const)
beta_const,gamma = mnmz.x[0],mnmz.x[1] #感染率、除去率(治癒率)
print(beta_const,gamma)
r0 = N*beta_const*(1/gamma)
print(r0)
以下でグラフ化します。
実効再生産数をプロットするためにax3,ax4の副軸を追加しています。
# plot reult with observed data
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(1.6180 * 4, 4*2))
ax3 = ax1.twinx()
ax4 = ax2.twinx()
lns1=ax1.plot(confirmed,"o", color="red",label = "data_I")
lns2=ax1.plot(confirmed_r,"o", color="green",label = "data_R")
est_i_0,est_i_1,est_i_2=estimate_i(ini_state,mnmz.x[0],mnmz.x[1])
lns3=ax1.plot(est_i_1, label = "estimation_I")
lns0=ax1.plot(est_i_2, label = "estimation_R")
lns_1=ax3.plot((S0-est_i_1-est_i_2)*r0/N,".", color="black", label = "effective_R0")
ax3.set_ylim(0,r0+1)
lns_ax1 = lns1+lns2 + lns3 + lns0 +lns_1
labs_ax1 = [l.get_label() for l in lns_ax1]
ax1.legend(lns_ax1, labs_ax1, loc=0)
ax1.set_ylim(0,N0)
ax1.set_title('SIR_{} f1_{:,d} f2_{:,d};N={:.0f} S0={:.0f} I0={:.0f} R0={:.0f} R={:.2f}'.format(city,f1,f2,N,S0,I0,R0,(S0-est_i_1[-1]-est_i_2[-1])*r0/N))
ax1.set_ylabel("Susceptible, Infected, recovered ")
ax3.set_ylabel("effective_R0")
以下で将来予測をグラフ化しています。
t_max=200 #len(days_from_22_Jan_20)
t=np.arange(0,t_max,dt)
lns4=ax2.plot(confirmed,"o", color="red",label = "data")
lns5=ax2.plot(confirmed_r,"o", color="green",label = "data_r")
est_i_0,est_i_1,est_i_2=estimate_i(ini_state,mnmz.x[0],mnmz.x[1])
lns6=ax2.plot(est_i_0, label = "estimation_S")
lns7=ax2.plot(est_i_1, label = "estimation_I")
lns8=ax2.plot(est_i_2, label = "estimation_R")
lns_6=ax4.plot((S0-est_i_1-est_i_2)*r0/N,".", color="black", label = "effective_R0")
lns_ax2 = lns4+lns5 + lns6 + lns7+ lns8 +lns_6
labs_ax2 = [l.get_label() for l in lns_ax2]
ax2.legend(lns_ax2, labs_ax2, loc=0)
ax4.set_ylim(0,r0+1)
ax2.set_ylim(0,S0)
ax2.set_title('SIR_{};b={:.2e} g={:.2e} r0={:.2f}'.format(city,beta_const,gamma,r0))
ax2.set_ylabel("Susceptible, Infected, recovered ")
ax4.set_ylabel("effective_R0")
ax1.grid()
ax2.grid()
plt.savefig('./fig/SIR_{}f1_{:,d}f2_{:,d};b_{:.2e}g_{:.2e}r0_{:.2f}N_{:.0f}S0_{:.0f}I0_{:.0f}R0_{:.0f}.png'.format(city,f1,f2,beta_const,gamma,r0,N,S0,I0,R0))
plt.show()
plt.close()
・日本の終息
データは2020年3月27日までのデータです。
データは以下のとおりです。
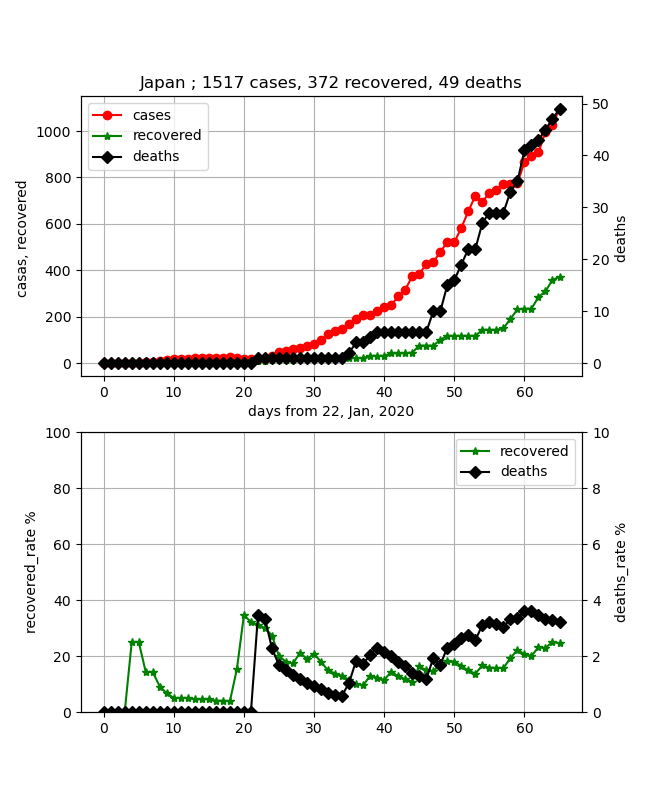
結果は以下のとおりです。
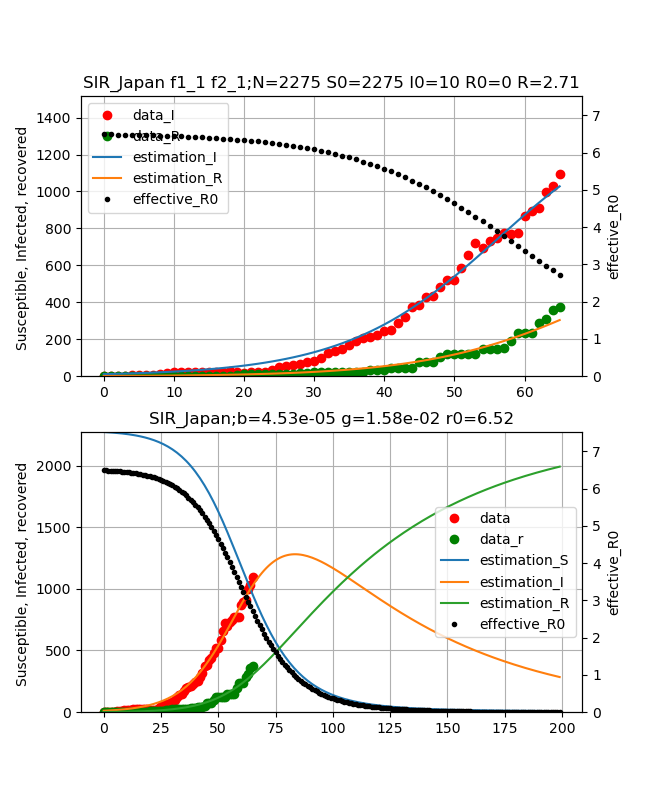
この結果はとりあえずフィッティング出来ているように見えますが、今日の報道見ていると昨日3月28日に200人感染と言っているので、それはこのグラフから上にはみ出ていて一致していません。
これについては、おまけに掲載しました。
得られた諸量は以下のとおりです。
{\begin{align}
\beta &= 4.53e^{-5}\\
\gamma &= 1.58e^{-2}\\
N &= 2275\\
R0 &= 6.52\\
R(27.3.2020) &= 2.71\\
\end{align}
}
・各国の終息
Hubei(武漢)の状況
最新(27.3.2020)のデータは以下のとおりです。
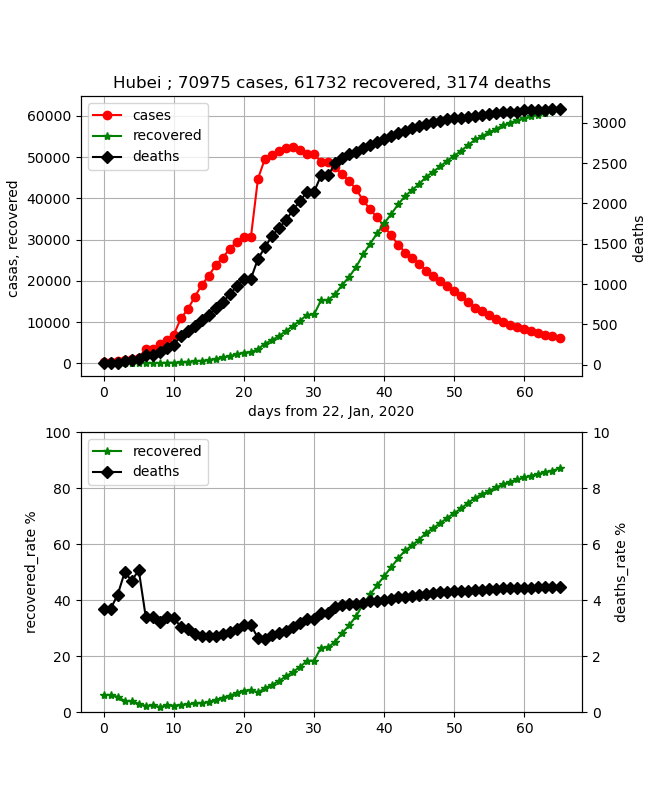
武漢のデータは感染数と治癒数の両方のデータをフィッティングしようとしても以下のとおり一致させることができません。
しかし、グラフ見てのとおり、実効再生産数R=0.01、0.08で終息したと言えます。
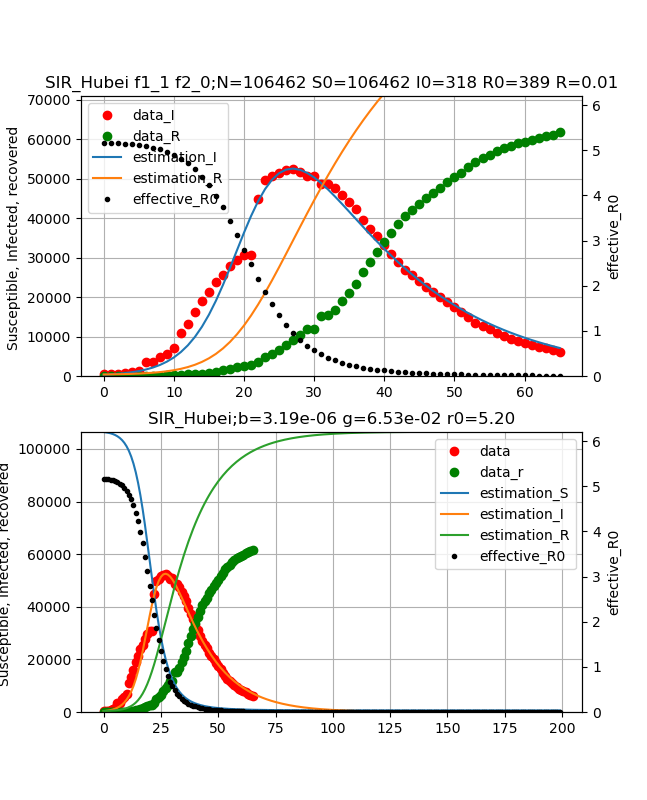
{\begin{align}
\beta &= 3.19e^{-6}\\
\gamma &= 6.53e^{-2}\\
N &= 106462\\
R0 &= 5.20\\
R(27.3.2020) &= 0.01\\
\end{align}
}
両方を同時にフィッティングしたものは以下のとおりで、感染数ピークが大幅にずれてしまっています。
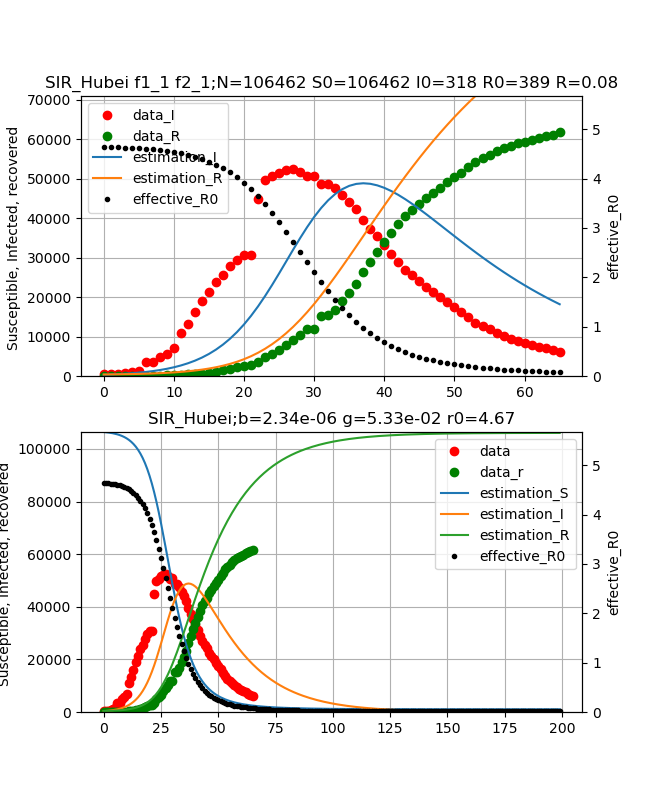
{\begin{align}
\beta &= 2.34e^{-6}\\
\gamma &= 5.33e^{-2}\\
N &= 106462\\
R0 &= 4.67\\
R(27.3.2020) &= 0.08\\
\end{align}
}
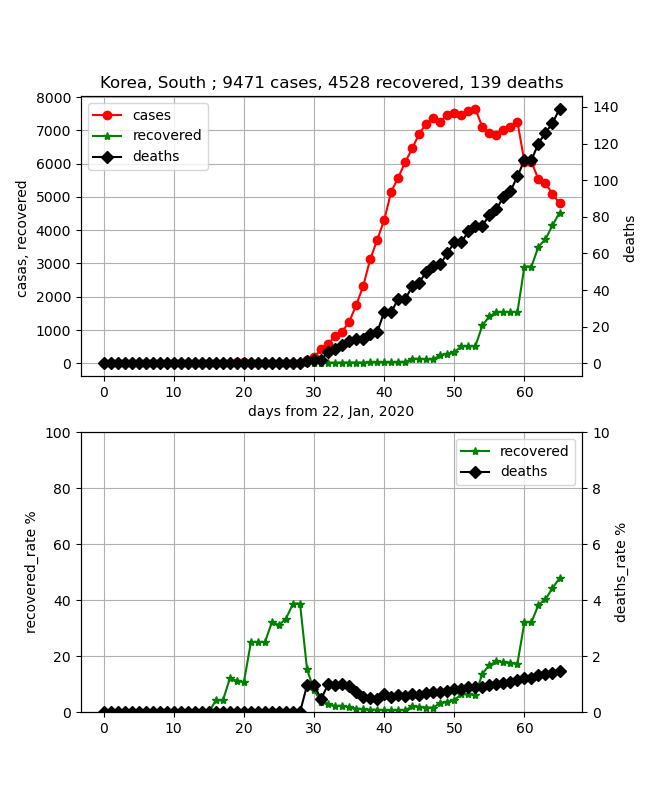
Korea, South(韓国)の状況
韓国のデータも武漢ほどひどくありませんが、ほぼ同様で感染数と治癒数の両方のデータをフィッティングしようとしても以下のとおり一致させることができません。
しかし、グラフ見てのとおり、実効再生産数R=0.13で終息しつつあります。
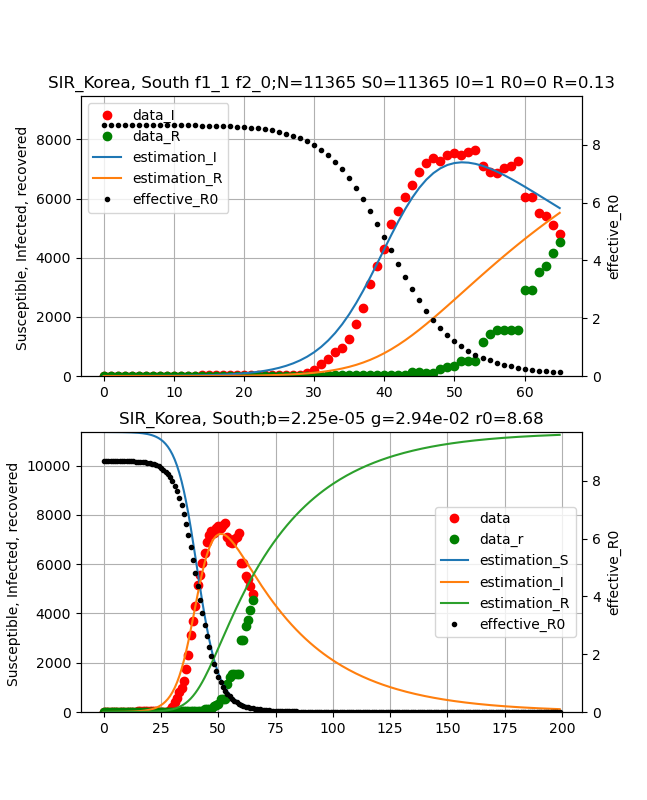
{\begin{align}
\beta &= 2.25e^{-5}\\
\gamma &= 2.94e^{-2}\\
N &= 11365\\
R0 &= 8.68\\
R(27.3.2020) &= 0.13\\
\end{align}
}
両方フィッティングしようとすると感染数データのフィッティングは甘くなり、感染ピークも右にずれてしまいます。もっときちんとフィッティングすれば合わせられるかもしれませんが、今回はこれ以上追求しません。
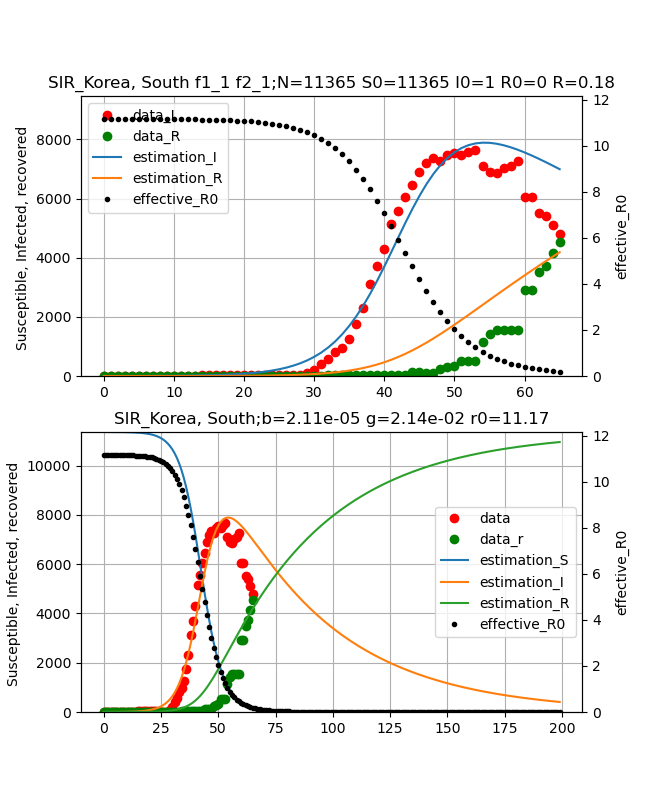
{\begin{align}
\beta &= 2.11e^{-5}\\
\gamma &= 2.14e^{-2}\\
N &= 11365\\
R0 &= 11.17\\
R(27.3.2020) &= 0.18\\
\end{align}
}
・Iran(イラン)の状況
次に終息が見込めそうな国はイランです。
最新(27.3.2020)のデータは以下のとおりです。
しかしここに来て治癒率が30%超えたところで停滞気味です。
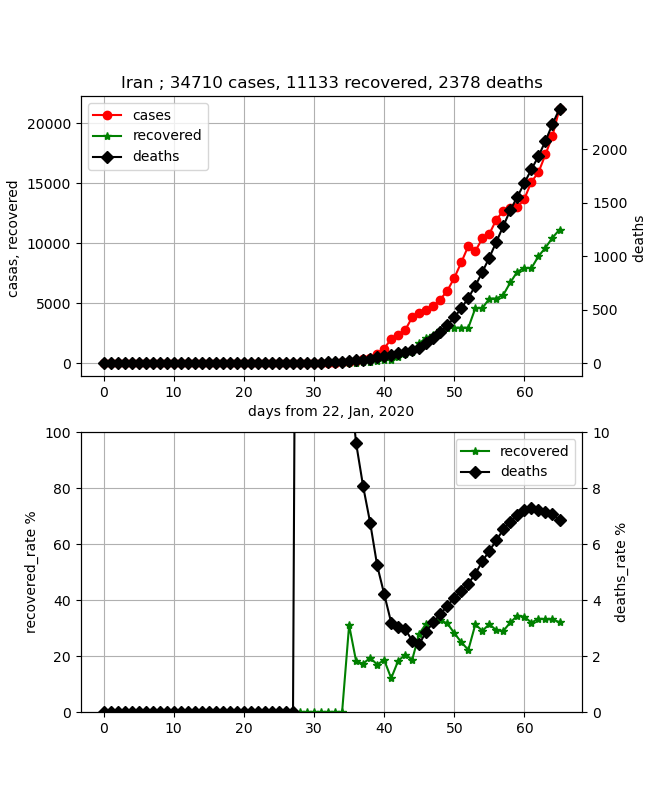
それでも、実効再生産数が1.81であり、もう少しで1になるので感染数ピークは近いと言えそうです。
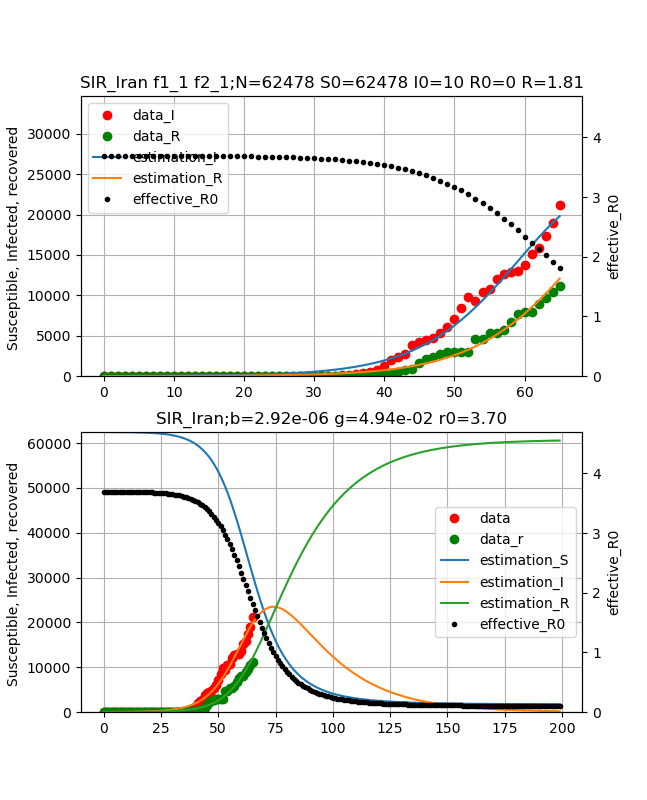
{\begin{align}
\beta &= 2.92e^{-6}\\
\gamma &= 4.94e^{-2}\\
N &= 62478\\
R0 &= 3.70\\
R(27.3.2020) &= 1.81\\
\end{align}
}
・Italy(イタリア)の状況
次に心配な国はイタリアです。
最新(27.3.2020)のデータは以下のとおりです。
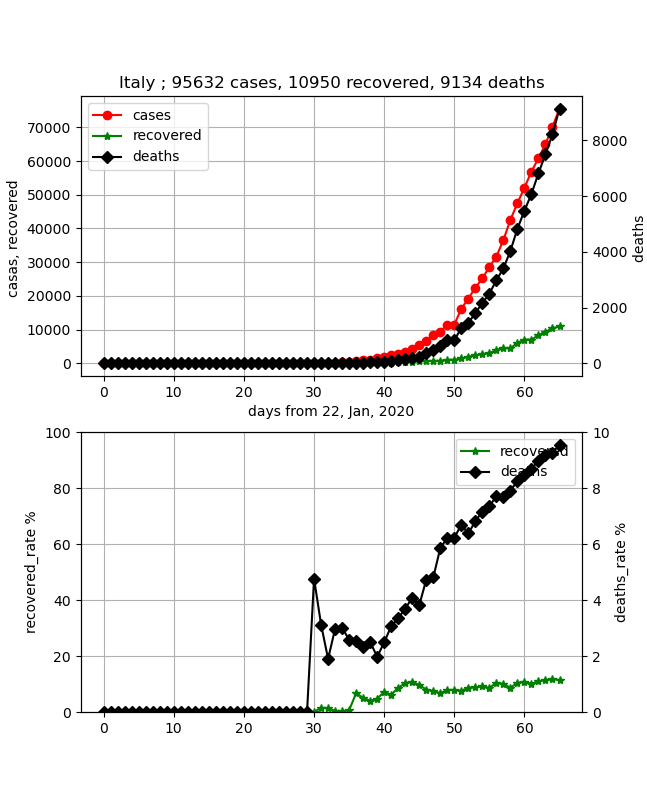
この国のデータはすごくしっかりしていて、感染数と治癒数の両曲線がぴったりフィッティング出来て気持ちいいです。結果は以下のとおりで、実効再生産数が4.07ですが急激に下がっており10日程で終息が見えそうです。
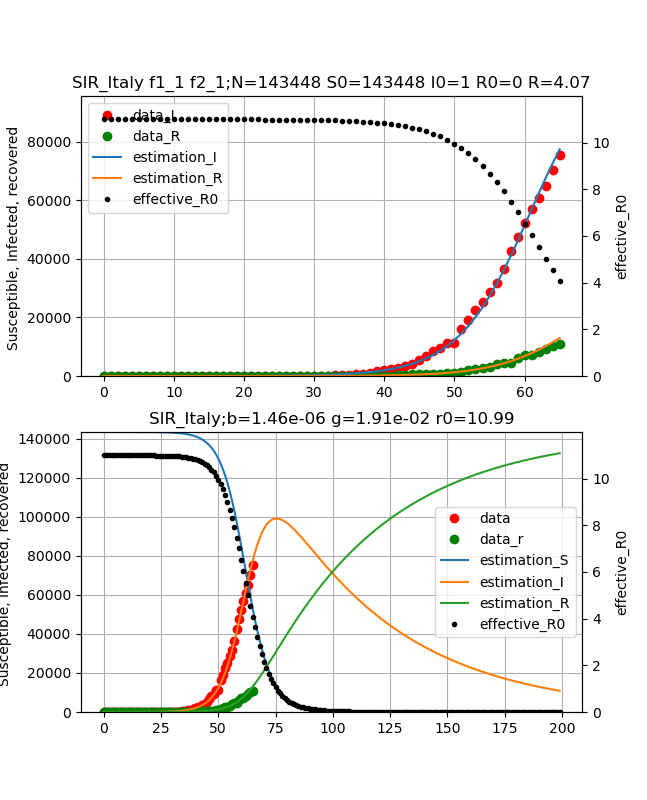
{\begin{align}
\beta &= 1.46e^{-6}\\
\gamma &= 1.91e^{-2}\\
N &= 143448\\
R0 &= 10.99\\
R(27.3.2020) &= 4.07\\
\end{align}
}
このデータを見る限りは医療崩壊はしていないし、都市封鎖の効果など管理がしっかりしている印象を受けます。(コメントはグラフ以外科学的根拠はありません。個人の印象です)
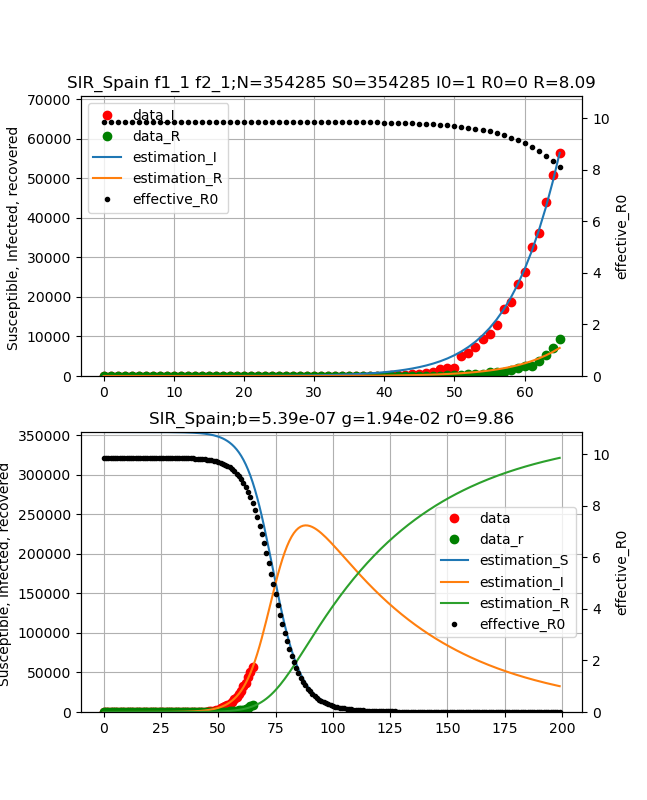
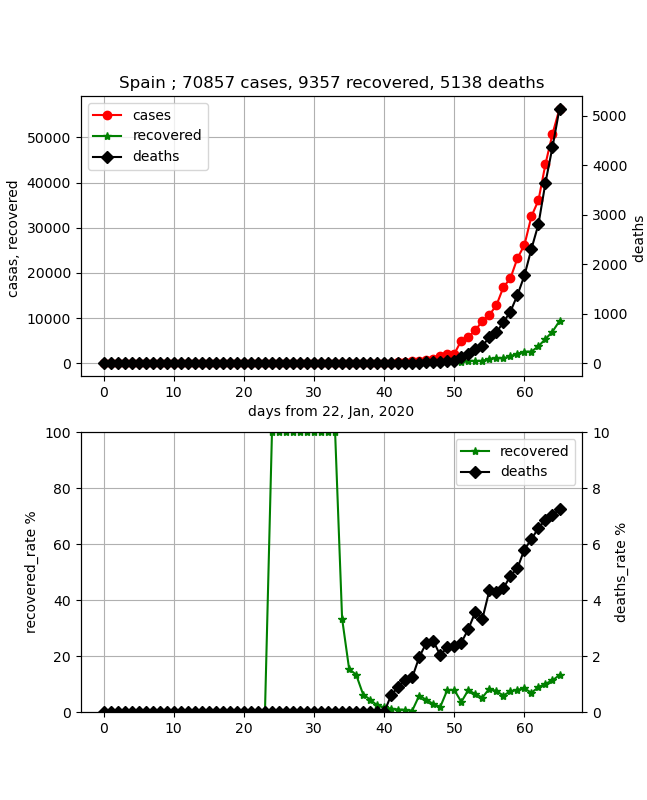
・Spain(スペイン)の状況
次に急激に死亡が増えているスペインの状況を示します。
結論書くとまだまだ初期拡大期に見えて、フィッティングは不定になっています。
※このモデルでは今は決めかねる状況
最新(27.3.2020)のデータは以下のとおりです。
以下Nの小さめの場合と大きくした場合を示します。
Nなどは不定ですが、実効再生産数はそれぞれ7.81, 8.09でまだまだですが、終息時期(感染ピーク)は80-90日(2週間から一月後)あたりにあり、ピーク値を無視すれば似たようなところにあると言えます。
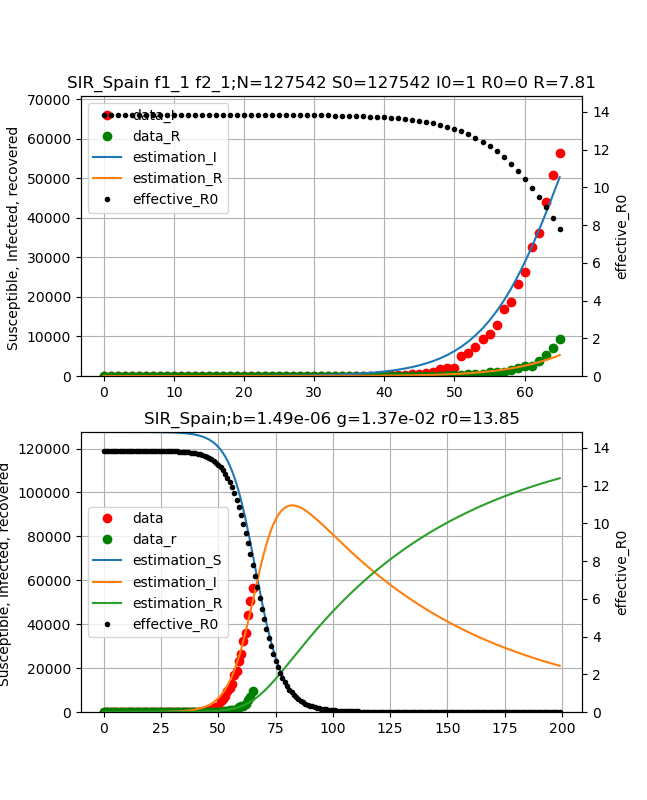
{\begin{align}
\beta &= 1.49e^{-6}\\
\gamma &= 1.37e^{-2}\\
N &= 127542\\
R0 &= 13.85\\
R(27.3.2020) &= 7.81\\
\end{align}
}
{\begin{align}
\beta &= 5.39e^{-7}\\
\gamma &= 1.94e^{-2}\\
N &= 354285\\
R0 &= 9.86\\
R(27.3.2020) &= 8.09\\
\end{align}
}
実は、ドイツ、フランス、スイスも同様ですが、フィッティングしようとしましたが急激な増加のため今回は(パラメータ不定)だったので改めて書こうと思います。
・ちょっと議論
あまり、真に受けられると困るので、ちょっと書いておきます。
このフィッティングの最大の欠点はN固定というところです。クローズドな対象者で自然発展的に感染伝播している状況はきちんとシミュレートできそうです。
しかし、世界の多くの国は完全なロックダウンを取っていないし、少なくともここまでは人の移動があり、しかもその中には感染者そのものも(割合として)多くいました。
日本は、今まさしくそういう外来感染者が増加しており、そこからさらにクラスター形成している状況もあります。
ということで、ここで書いたことはこれまでの推移のフィッティングであり、今後の状況を占うことはできません。これらの予測が当たるにはこれからも同じ状況が続くことが前提だし、外来感染者の割合を極度に管理できればという必要があります。
実際、これらの効果を考えたモデルは書けるけど、時々刻々ランダムに変化する外来感染者数を予測することが難しい以上、このモデルでは予測は不可能だと思われます。
ということで、欧米についても全体が見え始めればフィッティングも可能となるし、得られたパラメータについての議論もできると考えています。
まとめ
・COVID-19データをSIRモデルでフィッティングしてみた
・武漢は終息が近いし、韓国も終息に向かって感染ピークは越えたことが分かった
・イラン、イタリアは比較的早くあと10日程度で感染ピークが来ると期待できる
・日本は、だらだら飽和なので比較的感染ピークは遅く、外来感染者次第だがあと20日で感染ピークが来ると期待できる
・現状の状況が進めば多くの国であとひと月すると感染ピークが見え始めると考えられる
・日々監視して状況変化を見たいと思う
・得られたパラメータの評価をやりたいと思う
おまけ
今、データ見たら2020年3月28日まで反映されていたのでフィッティングしてみました。
しかし、昨日のデータは異常値となっており、感染ピークの時期はあまり変化ありません。
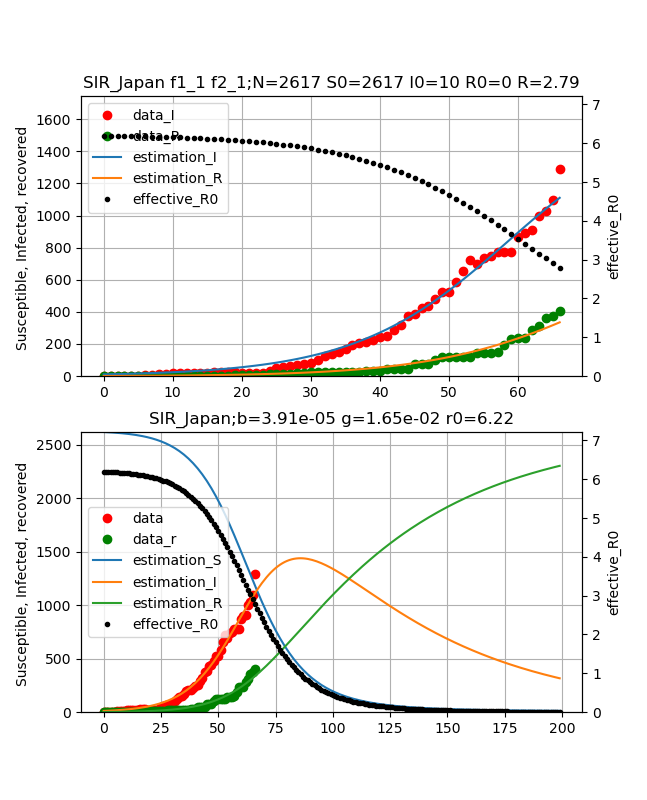
得られたパラメータは以下のとおりで、上記と比べてもあまり変化していません。
しかし、実効再生産数Rがわずかですが、上がっているので要注意です。
{\begin{align}
\beta &= 3.91e^{-5}\\
\gamma &= 1.65e^{-2}\\
N &= 2617\\
R0 &= 6.22\\
R(28.3.2020) &= 2.79\\
\end{align}
}
これからの動向を見たいと思います。