今回は、フォルマント合成をよりリアルに近づけるために、FFTした周波数と振幅を利用して、リアルタイムでフォルマント合成して発生するというのをやったみた。
時間分解まではできていないので、まだまだの感はあるが一応記事にしておく。
フォルマント合成については、以下の記事を見てください
【参考】
・【Audio入門】Sin波のフォルマント合成で音声を再現してみる♬
・【Audio入門】Sin波の合成でメロディや音声を再現・再生してみる♬
コードは以下に置いた
・AudioAutoencoder/out_fft_sound.py
コード解説
使うライブラリは以下のものです。
import numpy as np
from matplotlib import pyplot as plt
import wave
import struct
import pyaudio
from scipy.fftpack import fft, ifft
import cv2
from scipy import signal
import matplotlib
マイク入力の設定は以下のとおりです。
sec=1として、1秒測定としていますが、これは適当な数字でやってみてください。
CHUNKも同様で、適当な数字でOKです。
# パラメータ
RATE=44100
sec =1 #秒
CHUNK=RATE*sec
p=pyaudio.PyAudio()
sa= 'u' #'u' #'o' #'i' #'e' #'a'
stream=p.open(format = pyaudio.paInt16,
channels = 1,
rate = RATE,
frames_per_buffer = CHUNK,
input = True,
output = True) # inputとoutputを同時にTrueにする
fr = RATE #サンプリング周波数
fn=fr*sec
以下でフォルマント合成を実施しています。
まず、sin関数にA;振幅 f0; 振動数 fr;サンプリング周波数 t;時間配列を与えるとsin_wav;配列を戻します。
def sin_wav(A,f0,fr,t):
point = np.arange(0,fr*t)
sin_wav =A* np.sin(2*np.pi*f0*point/fr)
return sin_wav
以下で上の関数使ってサイン波生成とそれをwavfileに格納して保存している。
def create_wave(A,f0,fr,t):#A:振幅,f0:基本周波数,fr:サンプリング周波数,再生時間[s]
sin_wave=0
#print(A[0])
int_f0=int(f0[0])
for i in range(0,len(A),1):
f1=f0[i]
sw=sin_wav(A[i],f1,fr,t)
sin_wave += sw
sin_wave = [int(x * 32767.0) for x in sin_wave]
binwave = struct.pack("h" * len(sin_wave), *sin_wave)
w = wave.Wave_write('./fft_sound/'+sa+'_'+str(sec)+'Hz.wav')
p = (1, 2, fr, len(binwave), 'NONE', 'not compressed')
w.setparams(p)
w.writeframes(binwave)
w.close()
以下が上記で保存したwavfileを呼び出してsigに代入して返す関数。
※ちなみに既存のwavfileも以下のwavfileに与えてやれば対応できる
def sound_wave(fu):
int_f0=int(fu)
wavfile = './fft_sound/'+sa+'_'+str(sec)+'Hz.wav'
wr = wave.open(wavfile, "rb")
input = wr.readframes(wr.getnframes())
output = stream.write(input)
sig =[]
sig = np.frombuffer(input, dtype="int16") /32768.0
return sig
以下で、マイク音声を取得してinputに代入している。
さらに、sigに変換して生データとしてwavfileに保存している。
t = np.linspace(0,sec, fn)
input = stream.read(CHUNK)
sig =[]
sig = np.frombuffer(input, dtype="int16") /32768.0
# サイン波を-32768から32767の整数値に変換(signed 16bit pcmへ)
swav = [int(x * 32767.0) for x in sig]
# バイナリ化
binwave = struct.pack("h" * len(swav), *swav)
w = wave.Wave_write("./fft_sound/output_"+str(sec)+"_"+sa+".wav")
params = (1, 2, fr, len(binwave), 'NONE', 'not compressed')
w.setparams(params)
w.writeframes(binwave)
w.close()
以下がFFT関数である。
FFTした信号sigの周波数と振幅を取得している。
※条件は適当な数値に変更する
def FFT(sig,fn,fr):
freq =fft(sig,fn)
Pyy = np.sqrt(freq*freq.conj())/fn
f = np.arange(0,fr,fr/fn)
ld = signal.argrelmax(Pyy, order=10) #相対強度の最大な番号をorder=10で求める
ssk=0
fsk=[]
Psk=[]
maxPyy=max(np.abs(Pyy))
for i in range(len(ld[0])): #ピークの中で以下の条件に合うピークの周波数fと強度Pyyを求める
if np.abs(Pyy[ld[0][i]])>0.1*maxPyy and f[ld[0][i]]<20000 and f[ld[0][i]]>20:
fssk=f[ld[0][i]]
Pssk=np.abs(Pyy[ld[0][i]])
fsk.append(fssk)
Psk.append(Pssk)
ssk += 1
#print('{}'.format(np.round(fsk[:len(fsk)],decimals=3))) #標準出力にピーク周波数fskを小数点以下二桁まで出力する
#print('{}'.format(np.round(Psk[:len(fsk)],decimals=4))) #標準出力にピーク強度Pskを小数点以下6桁まで出力する
return freq,Pyy,fsk,Psk,f
以下が信号及びFFTの結果などを描画する関数
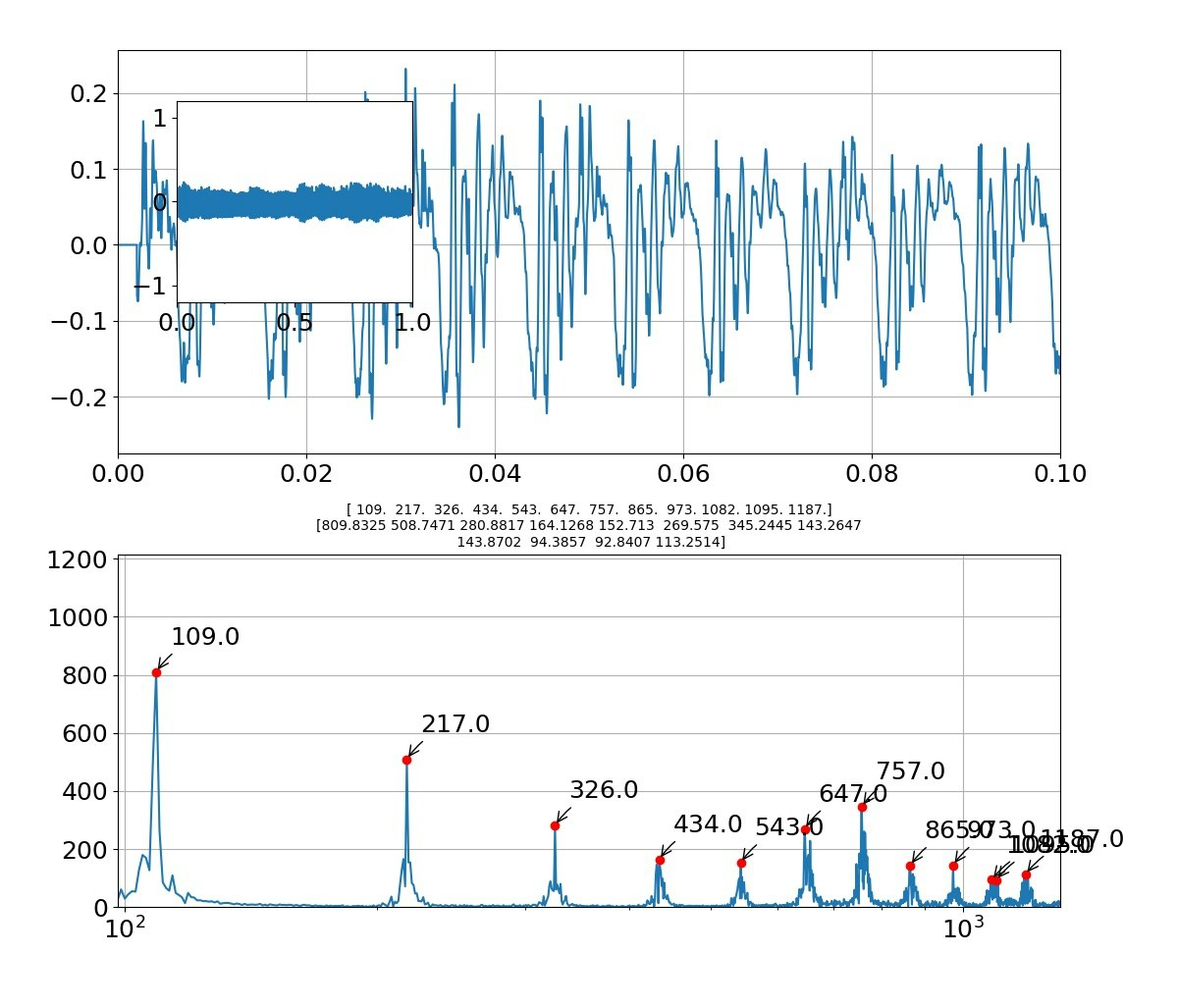
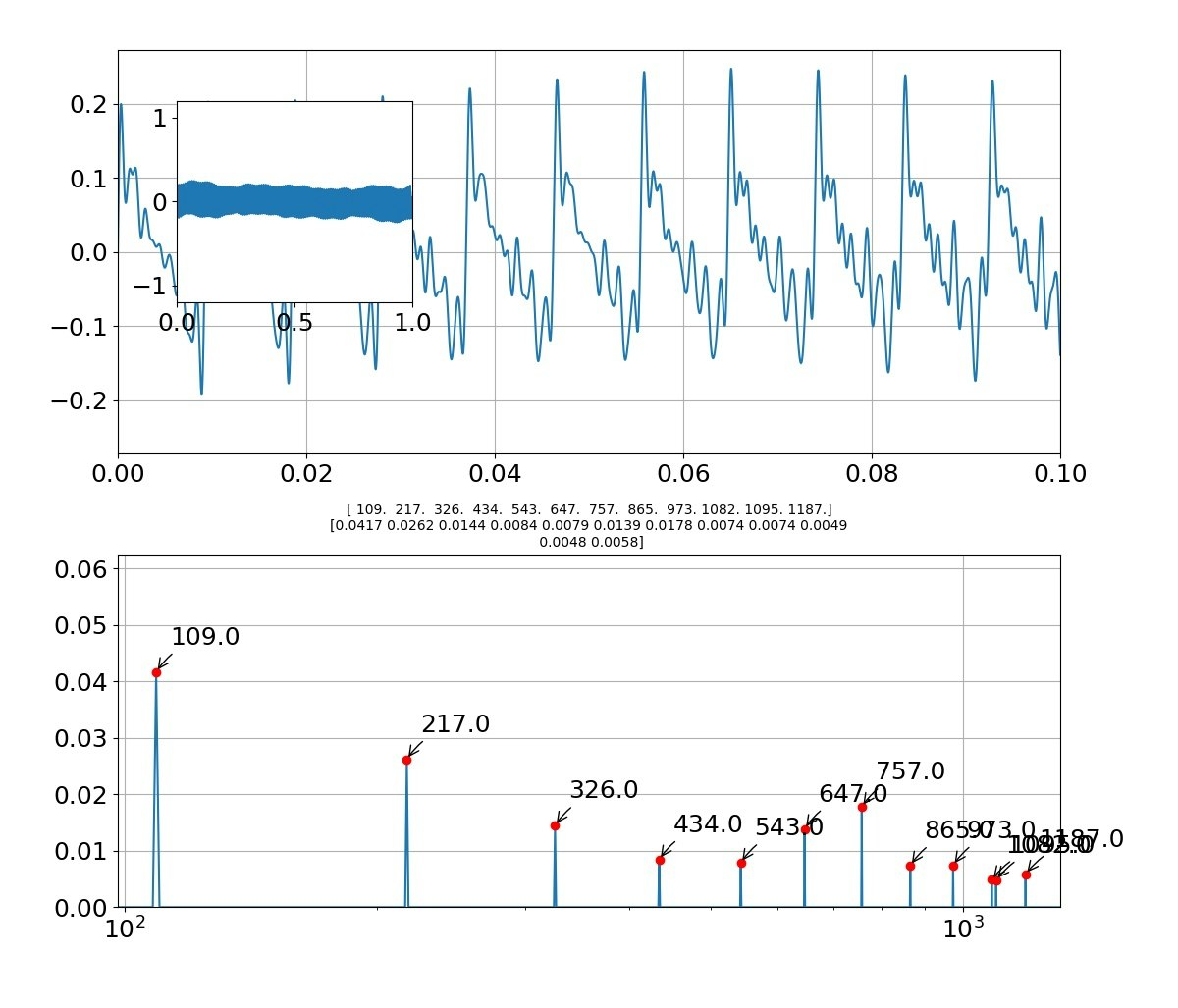
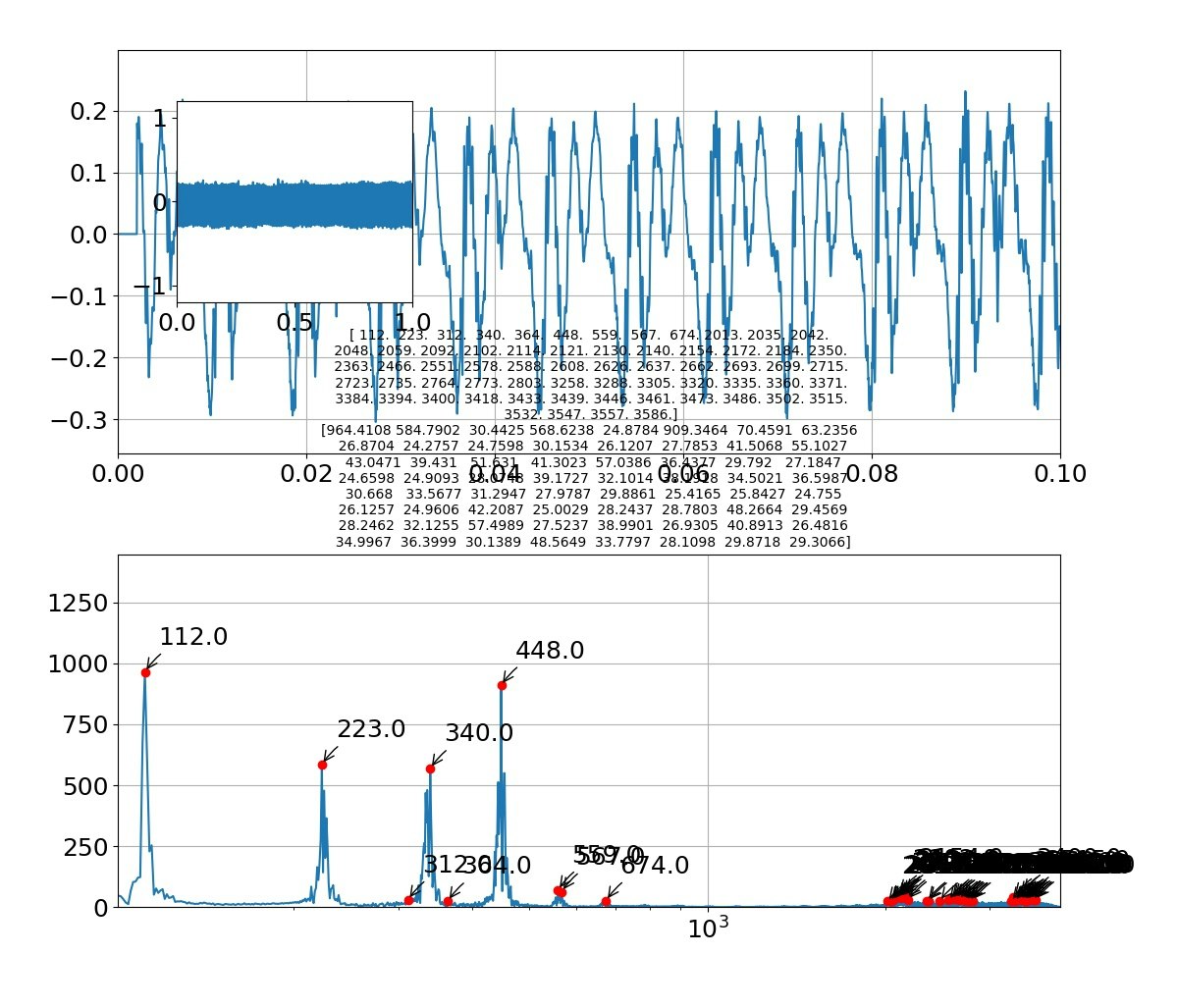
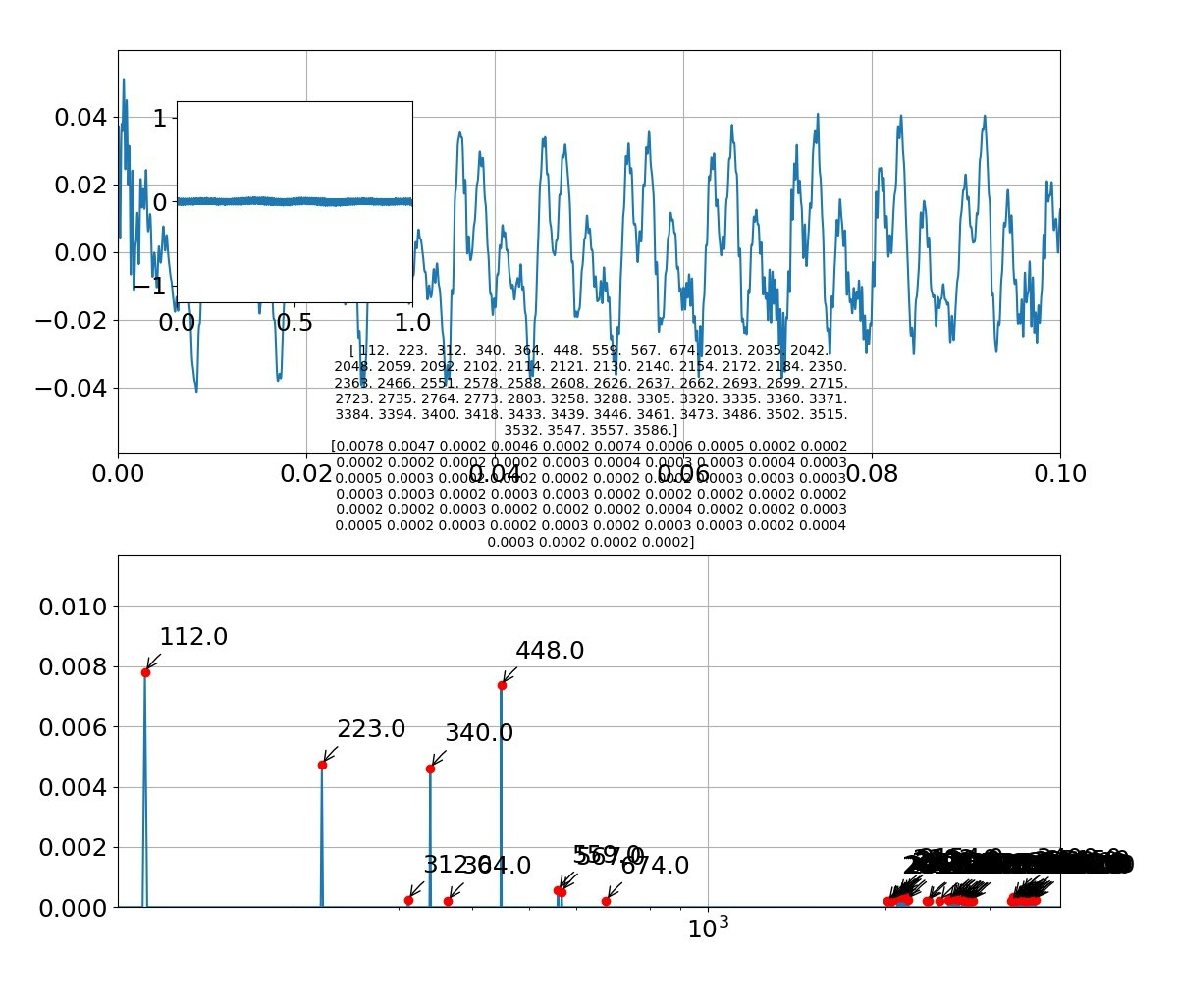
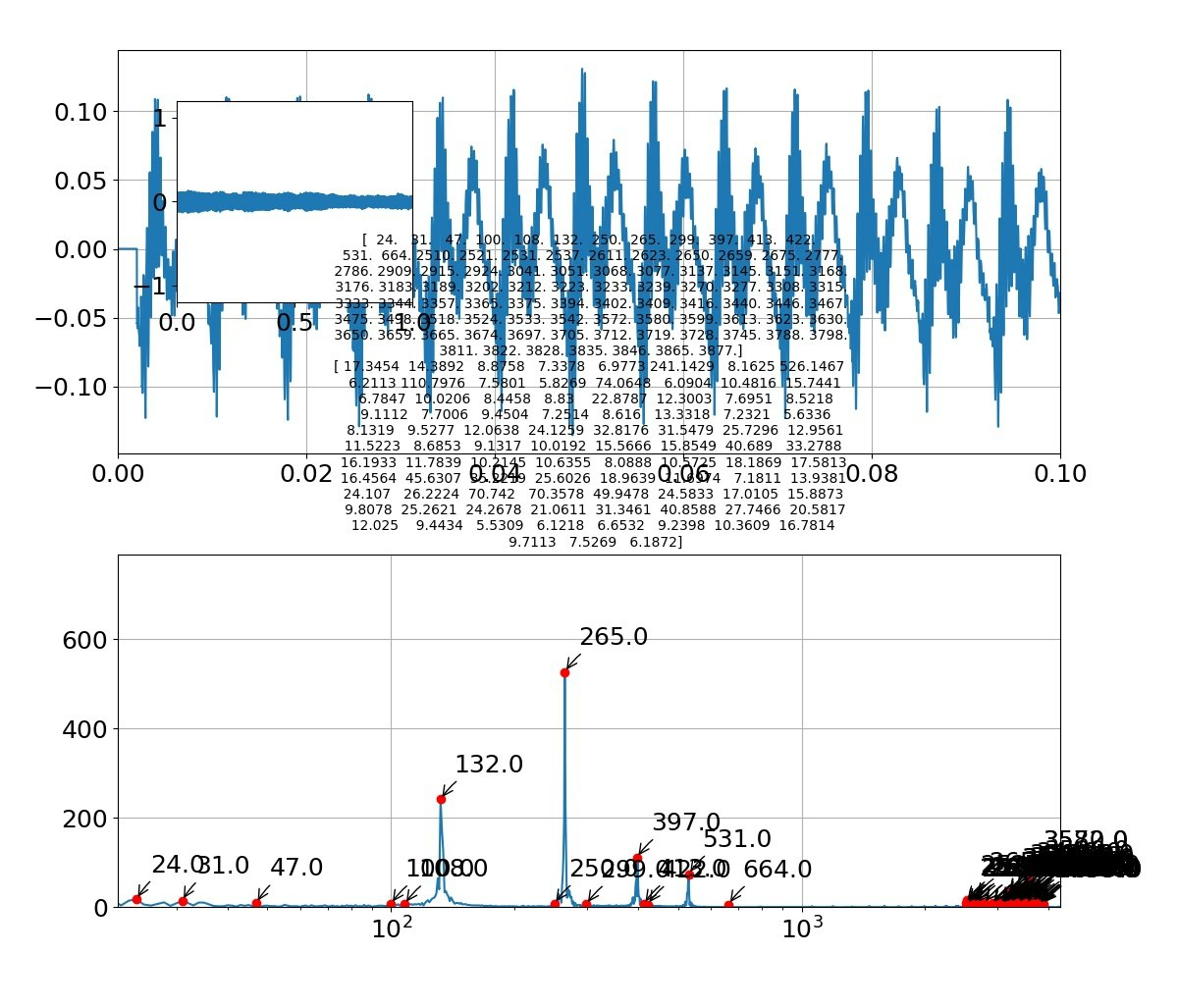
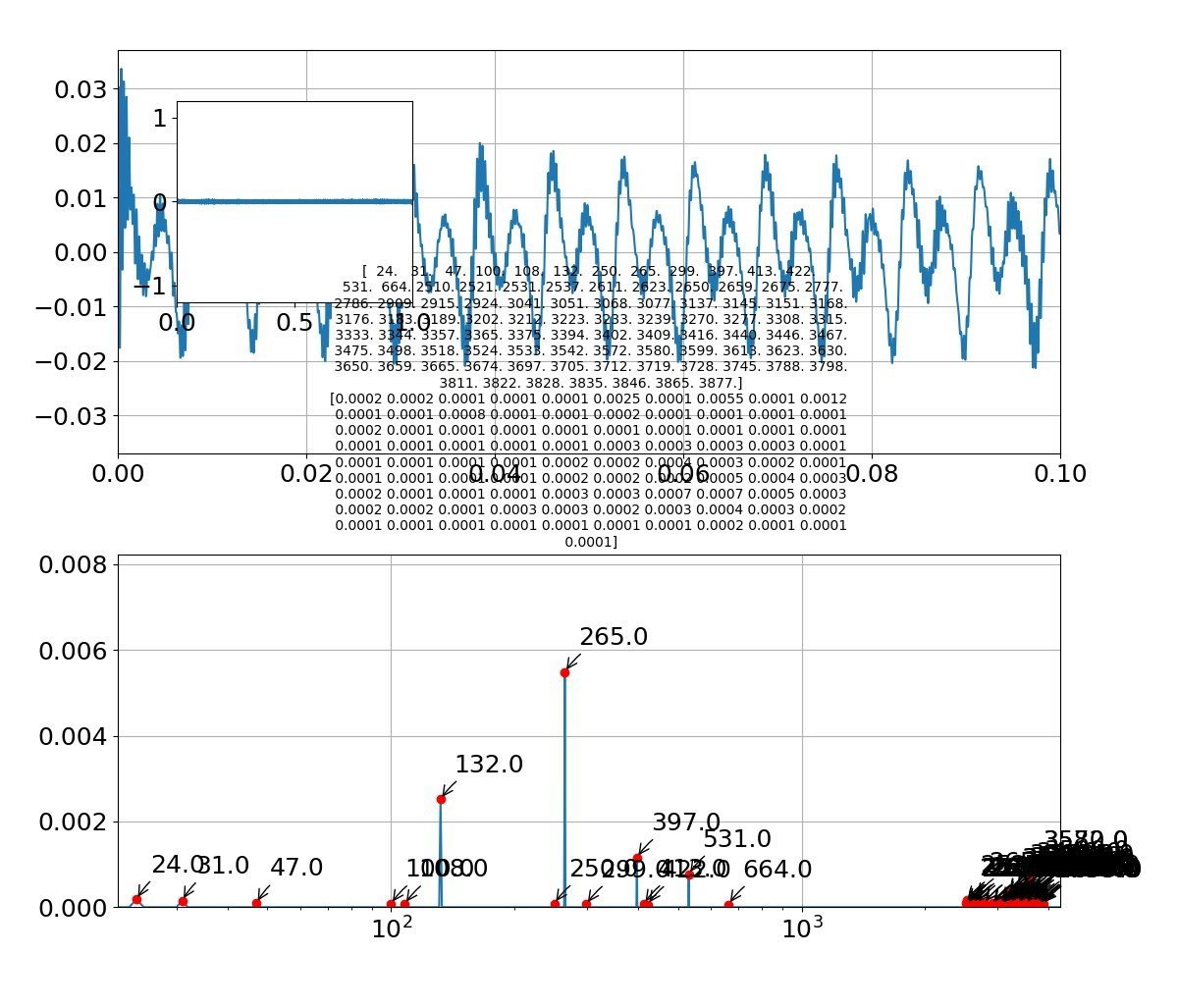
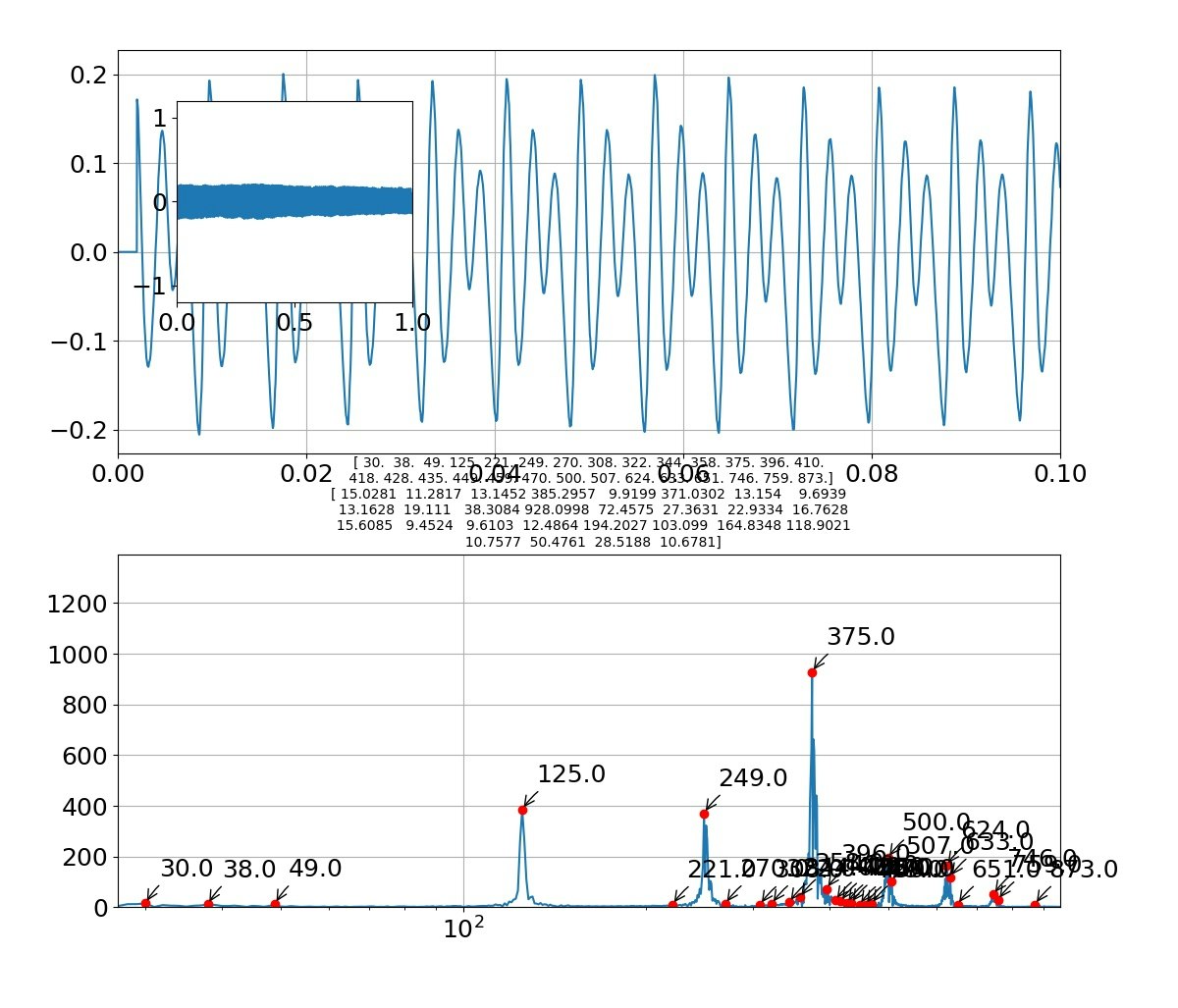
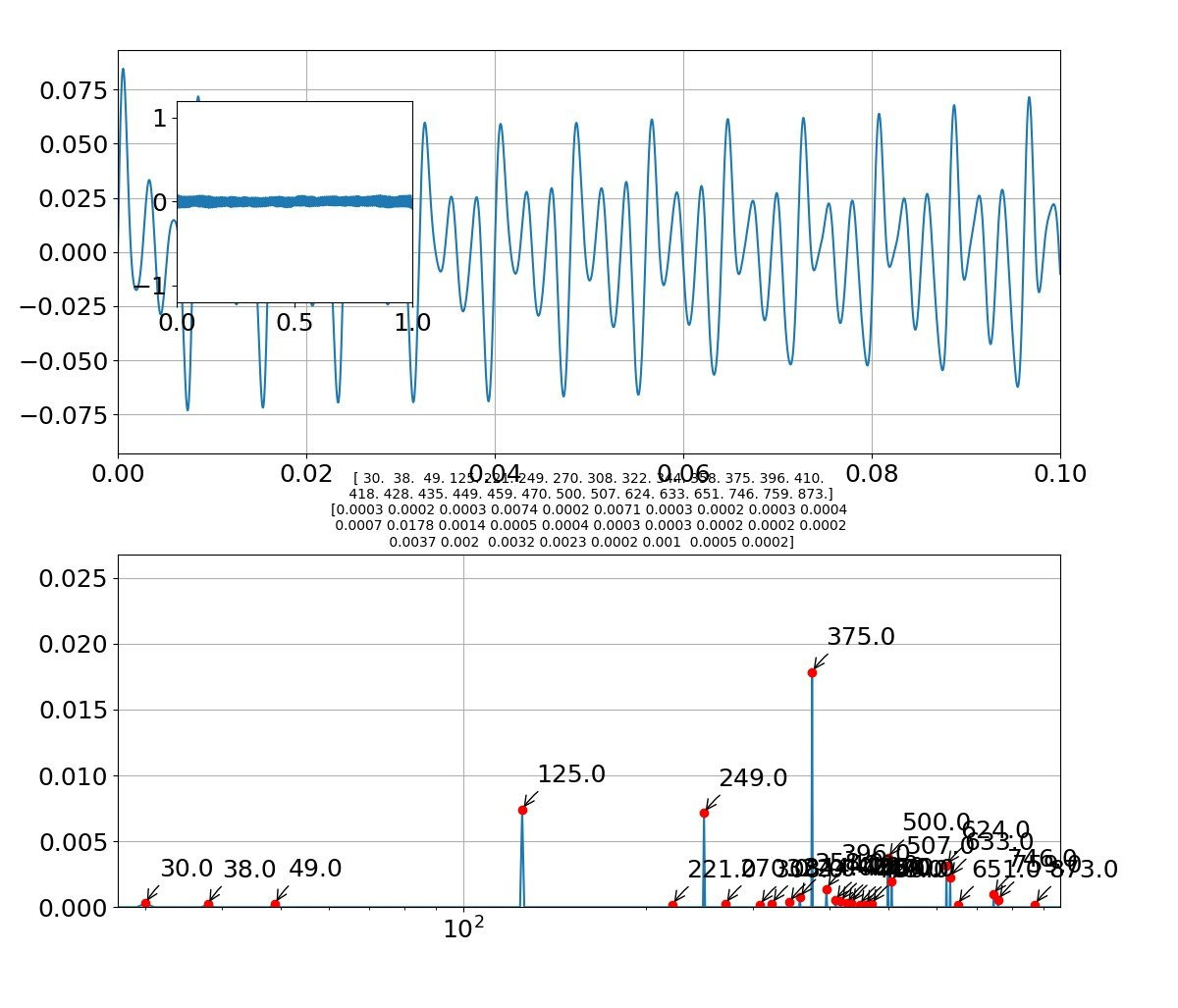
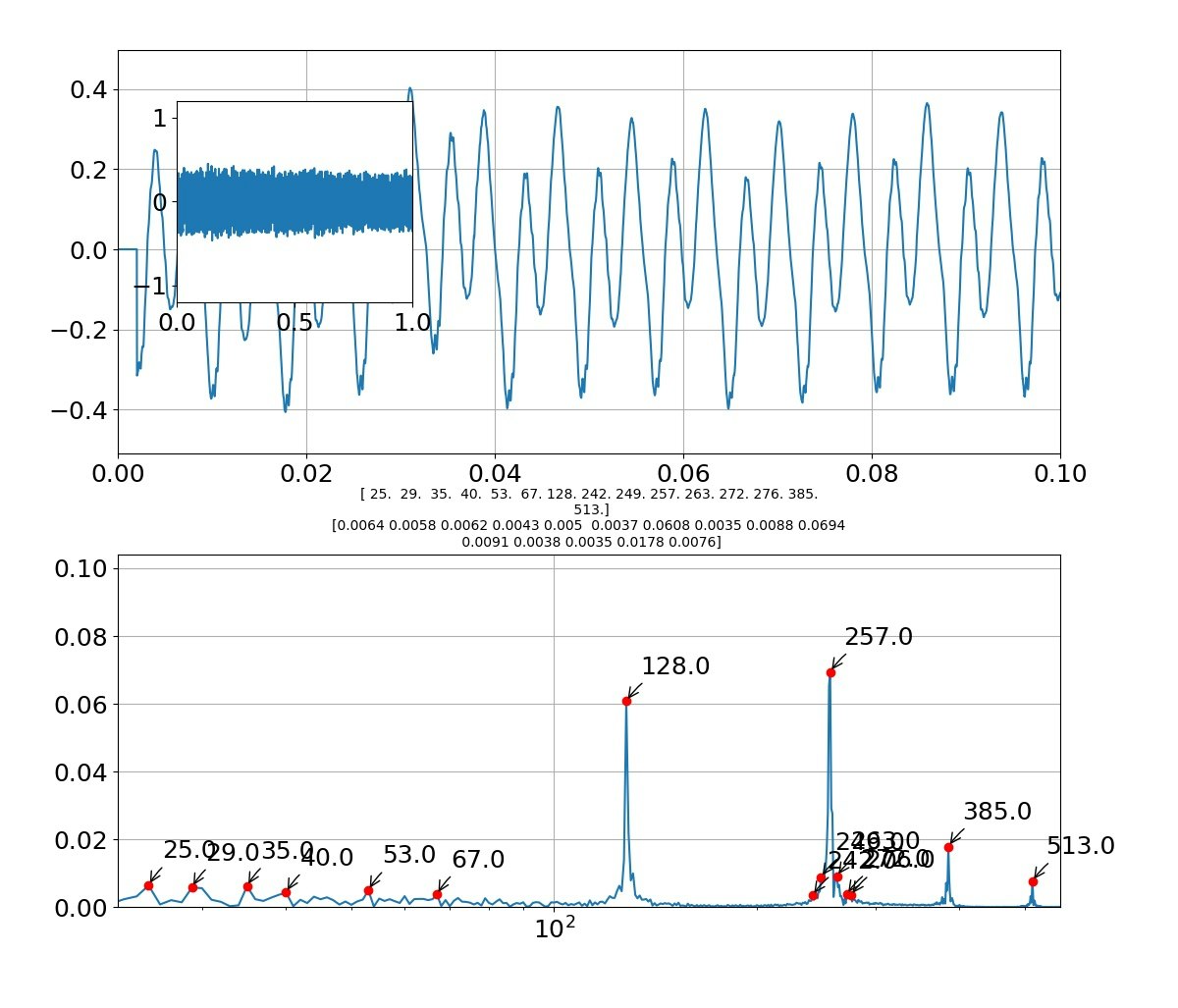
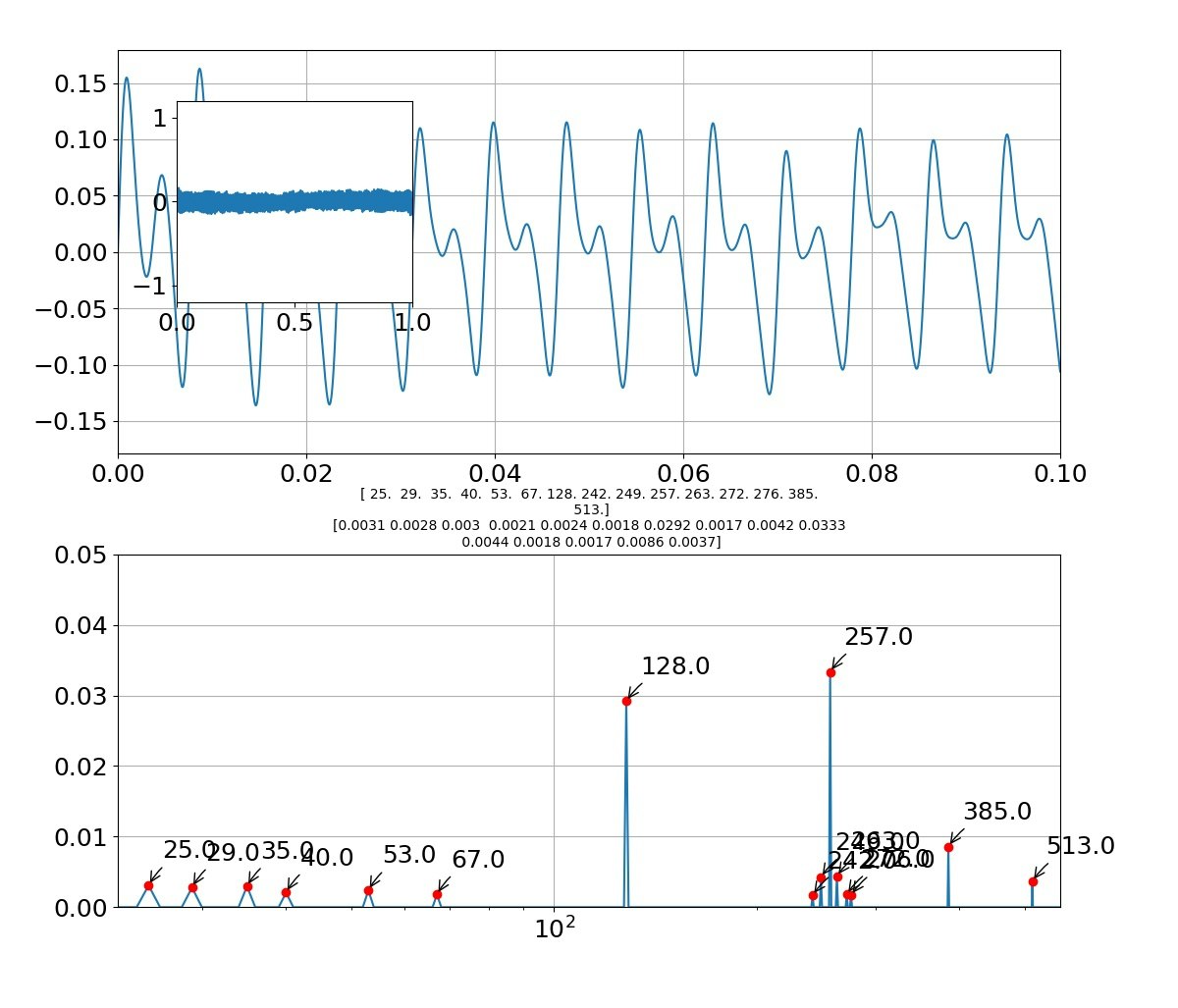
def draw_pic(freq,Pyy,fsk,Psk,f,sk,sig):
matplotlib.rcParams.update({'font.size': 18, 'font.family': 'sans', 'text.usetex': False})
fig = plt.figure(figsize=(12,12)) #(width,height)
axes1 = fig.add_axes([0.1, 0.55, 0.8, 0.4]) # main axes
axes2 = fig.add_axes([0.15, 0.7, 0.2, 0.2]) # insert axes
axes3 = fig.add_axes([0.1, 0.1, 0.8, 0.35]) # main axes
axes1.plot(t, sig)
axes1.grid(True)
axes1.set_xlim([0, 0.1])
axes2.set_ylim(-1.2,1.2)
axes2.set_xlim(0,sec)
axes2.plot(t,sig)
Pyy_abs=np.abs(Pyy)
axes3.plot(f,Pyy_abs)
axes3.axis([min(fsk)*0.9, max(fsk)*1.1, 0,max(Pyy_abs)*1.5]) #0.5, 2
axes3.grid(True)
axes3.set_xscale('log')
axes3.set_ylim(0,max(Pyy_abs)*1.5)
axes3.set_title('{}'.format(np.round(fsk[:len(fsk)], decimals=1))+'\n'+'{}'.format(np.round(Psk[:len(fsk)],decimals=4)),size=10) #グラフのタイトルにピーク周波数とピーク強度を出力する
axes3.plot(fsk[:len(fsk)],Psk[:len(fsk)],'ro') #ピーク周波数、ピーク強度の位置に〇をつける
# グラフにピークの周波数をテキストで表示
for i in range(len(fsk)):
axes3.annotate('{0:.1f}'.format(fsk[i]), #np.round(fsk[i],decimals=2) でも可 '{0:.0f}(Hz)'.format(fsk[i])
xy=(fsk[i], Psk[i]),
xytext=(10, 20),
textcoords='offset points',
arrowprops=dict(arrowstyle="->",connectionstyle="arc3,rad=.2")
)
plt.pause(1)
wavfile=str(sec)+'_'+sa+str(sk)
plt.savefig('./fft_sound/figure_'+wavfile+'.jpg')
plt.close()
#return Psk, fsk
以下が実際のメインである。
# 入力音声をFFTして描画する
freq,Pyy,fsk,Psk,f=FFT(sig,fn,fr)
draw_pic(freq,Pyy,fsk,Psk,f,1,sig)
# マイク入力をスピーカ出力
input = binwave
output = stream.write(input)
# FFTで得られた周波数Pskと振幅fsk
A=Psk/max(Psk)/len(fsk)
f=fsk
print(A)
# 上記のAとfを使ってサイン波でフォルマント合成
sigs =[]
create_wave(A, f, fr, sec)
sigs = sound_wave(f[0])
# フォルマント合成音声をFFTして描画する
freqs,Pyys,fsks,Psks,fss=FFT(sigs,fn,fr)
draw_pic(freqs,Pyys,fsks,Psks,fss,2,sigs)
while True:
#永続的にフォルマント合成音を発生する
sig =[]
create_wave(A, f, fr, sec)
sig = sound_wave(f[0])
結果
結果評価
・音はだいたい再現できたレベル。やはり、グラフの類似性見てももっとという感じが残る
・フォルマント合成については、どの母音も一応主振動に関しては、よく成り立っていると言える。
例えば「お」をよく見ると以下のような周波数になっている
[25,29,35,40,53,67,128,142,249,257,263,272,276,385,513]
となっており、振幅の大きいところが主振動と考えると、以下のように基準振動128Hzで規則性が見られる。
[128,257(+127),385(+128),513(+128)]
一方、
また、低い振動数領域も以下のとおりの規則性がある。
[25,29(+4),35(+6),40(+5),53(+13),67(+14)]
そして、例えば257の周りにサブなサテライト振動が見えるが、これは以下のように解釈できる。
[249(-8),257(基準),263(+6),272(+15)]
とみれば、主振動257の周りに第一サテライトに±8があり、第二サテライトに+15があると見える。
つまり、主振動だけでなく小さな振動要素が重ね合わさっているので厳密な意味でフォルマント合成ができるわけではなさそうである。
※あくまで、そういう原理で発生しているとみるべきである
・実は、「か」などもやってみた。しかし、「k」「a」であり、この手法ではうまく再現できなかった。ここは実は参考のような原理になっている。
ということで、今回の技術と合わせ技で五十音をリアルタイムで再現したいと思う。
【参考】
・【Scipy】FFT、STFTとwavelet変換で遊んでみた♬~音声合成アプリ
オリジナルと合成した音声は以下に置いた
合成音声
・AudioAutoencoder/wavfile/melody0.wav
オリジナル音声
・AudioAutoencoder/wavfile/melody1.wav
聞き比べるとかなり再現している。
※ダウンロードしてお聞きください
まとめ
・FFT利用のリアルタイム・フォルマント音声合成をやってみた
・基準振動についてはフォルマント合成が成り立っているが詳細部分ではサテライト振動が発現していることが分かった
・母音以外の音声については、さらに工夫が必要である
・子音について、別方法を利用して統合して50音に対してフォルマント合成を完成したい