【Audio入門】Sin波のフォルマント合成で音声を再現してみる♬

フォルマント合成が謎ですが、どうやらFFTした振幅の大きい順に並べてその周波数の波を合成する手法のようです。
【参考】
・①Android: フォルマント合成で母音を合成してみる

フォルマント合成

この手法だと、高調波の重ね合わせで音を出しているので、波形が乱れず音も一応それらしく聞こえます。
参考②に原理的な絵とフォルマントについての説明がありますが、今一つ理解ができません。
スライド１６を見ると、だいたいは円柱菅の開口端の振動みたいなものをイメージし、途中の部分で絞ったり抜けたりして制御する系を想定しているようです。
なので、基本は固有振動数ということになります。
【参考】
・②音声生成の基礎と音声学
・③開管の固有振動@気柱の振動
フォルマント合成は参考①によると以下のようなものです。
つまり、基準振動260の整数倍でフォルマント；振幅が大きい順に並べた振動の合成ということになります。
「あ」

フォルマント	周波数	振幅
１	1040	0.19
２	520	0.09
３	780	0.08
４	1300	0.08
５	260	0.07
６	1560	0.07

この整理を振動数をキーにして並べ替えると以下のようになります。

周波数	あ	い	う	え	お
f0(260)	0.07	0.19	0.19	0.19	0.08
2*f0	0.09	0.09	0.08	0.09	0.09
3*f0	0.08			0.08	0.08
4*f0	0.19		0.08	0.07	0.19
5*f0	0.08		0.08
6*f0	0.07		0.09
11*f0		0.08		0.08
12*f0		0.07
13*f0		0.08

一方、参考①が参考にしているニコニコ動画の各周波数の振幅は以下のとおりです。

周波数	あ	い	う	え	お
f0(260)	0.07	0.52	0.32	0.18	0.11
2*f0	0.09	0.03	0.11	0.14	0.14
3*f0	0.08			0.13	0.10
4*f0	0.19		0.02	0.03	0.24
5*f0	0.08		0.02
6*f0	0.07		0.13
11*f0		0.02		0.03
12*f0		0.01
13*f0		0.02

ということで、以下のコードにより、上記の振動数のサイン波を合成して母音の音声合成をします。
以下で通常のサイン波を求めます。

def sin_wav(A,f0,fs,t):
    point = np.arange(0,fs*t)
    sin_wav =A* np.sin(2*np.pi*f0*point/fs)
    return sin_wav

特定の周波数と振幅を使って、上記のサイン波の関数を呼び出して、サイン波を計算して合成します。

def create_wave(A,f0,fs,t):#A:振幅,f0:基本周波数,fs:サンプリング周波数,再生時間[s]
    sin_wave=0
    print(A[0])
    int_f0=int(f0[0])
    for i in range(0,len(A),1):
        f1=f0[i]
        sw=sin_wav(A[i],f1,fs,t)
        sin_wave += sw
    sin_wave = [int(x * 32767.0) for x in sin_wave]    
    binwave = struct.pack("h" * len(sin_wave), *sin_wave)
    w = wave.Wave_write('./aiueo/'+s+'/'+sa+'/'+str(int_f0)+'Hz.wav')
    p = (1, 2, fs, len(binwave), 'NONE', 'not compressed')
    w.setparams(p)
    w.writeframes(binwave)
    w.close()

上記で計算したwavfileを読み込んで、音声を出力します。
そして、信号sigを求めます。

def sound_wave(fu):
    int_f0=int(fu)
    wavfile = './aiueo/'+s+'/'+sa+'/'+str(int_f0)+'Hz.wav'
    wr = wave.open(wavfile, "rb")
    input = wr.readframes(wr.getnframes())
    output = stream.write(input)
    sig =[]
    sig = np.frombuffer(input, dtype="int16")  /32768.0
    return sig

上記の３の関数を使うと、以下のようにして母音を計算してかつ発生し、さらにFFT処理などができます。

A=(0.07,0.09,0.08,0.19,0.08,0.07) #a
f0=261.626
f=(f0,2*f0,3*f0,4*f0,5*f0,6*f0) #a
create_wave(A, f, fs, sec)
sig = sound_wave(f[0])
freq =fft(sig,int(fn))

※上記でfs,fnはサンプリングレートです
※今回は追求しませんが、両者を比較するとF1~F3当たりの順番はほぼ一致していますが、大きさ（比）はそれなりに異なるので、本来はもっと最適な値があるようです。
※絶対値は音の大きさなので、適当に規格化するのがいいと思います
一方、f0は何にするのがいいのか。。。これは人の声の高低に当たります。

ドレミの階調で高低な母音を合成する

そして、前回も書きましたが、いわゆる階調で変更したいと思います。
【参考】
④音階の周波数
参考④を見ると、周波数の級数的に並んでいて、以下の式で求められることが分かります。
「１オクターブには１２の音があり（ド~シ）、その１２の音は、隣り合う半音間での周波数の比率が同じです。．．．a12=a0r12=2a0からr=$^{12}\sqrt(2)$=1.059463094」
ということで、基準周波数f0を音階で変更したいときは、以下のような関数を定義することにより、システマティックに変更できます。

def B(a0=220):
    B=[]
    r= 1.059463094
    b=1
    for n in range(60):
        b *= r
        B.append(b*a0)
    return B

この関数を使うと、各母音に対して、基準周波数を変更するには以下のようにすればよくなります。
以下の関数を用意して、今の繰り返し位置skから新しい基準振動を計算します。
※６０個で元に戻るようにしています

B=B(27.5)
sk=0
def skf(sk):
    skf=sk
    skf = skf+1
    skf=skf%60
    print(skf)
    f0=B[skf]
    return f0,skf

キーを押したときに以下のようにfoや振幅Aを選択して、上記の

create_wave(A, f, fs, sec)
sig = sound_wave(f[0])

を計算してやればよいことになります。

    k = cv2.waitKey(0)
    if k == 27:         # wait for ESC key to exit
        cv2.destroyAllWindows()
        break
    elif k == ord('a'):
        cv2.imwrite('./aiueo/' +s+ '/' +sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='a'
        f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0,5*f0,6*f0)
        A=(0.07,0.09,0.08,0.19,0.08,0.07) #qiita        
    elif k == ord('z'):
        cv2.imwrite('./aiueo/'+s+'/' +sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='a'
        f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0,5*f0,6*f0) 
        A=(0.07,0.09,0.08,0.19,0.08,0.07)  #qiita        

コード全体はいかのリンクに置くとともに、おまけに載せました。
・AudioAutoencoder/make_wavUfile_function.py

結果

実際聞いた感じは、少しあの金属的な音ですが、一応「あ、え、い、お、う」と聞こえます。
ただし、それも中間的な以下のような周波数領域ではの話で、周波数が低すぎる場合も高い場合も今一つ再現性は悪い結果です。

そして、信号の波形やFFTの波形も一番いいと感じられる１３０あたりでも、以下のとおり、リアルなウワンの母音と比較すると、まだまだな結果となっています。
「あ；ウワン」

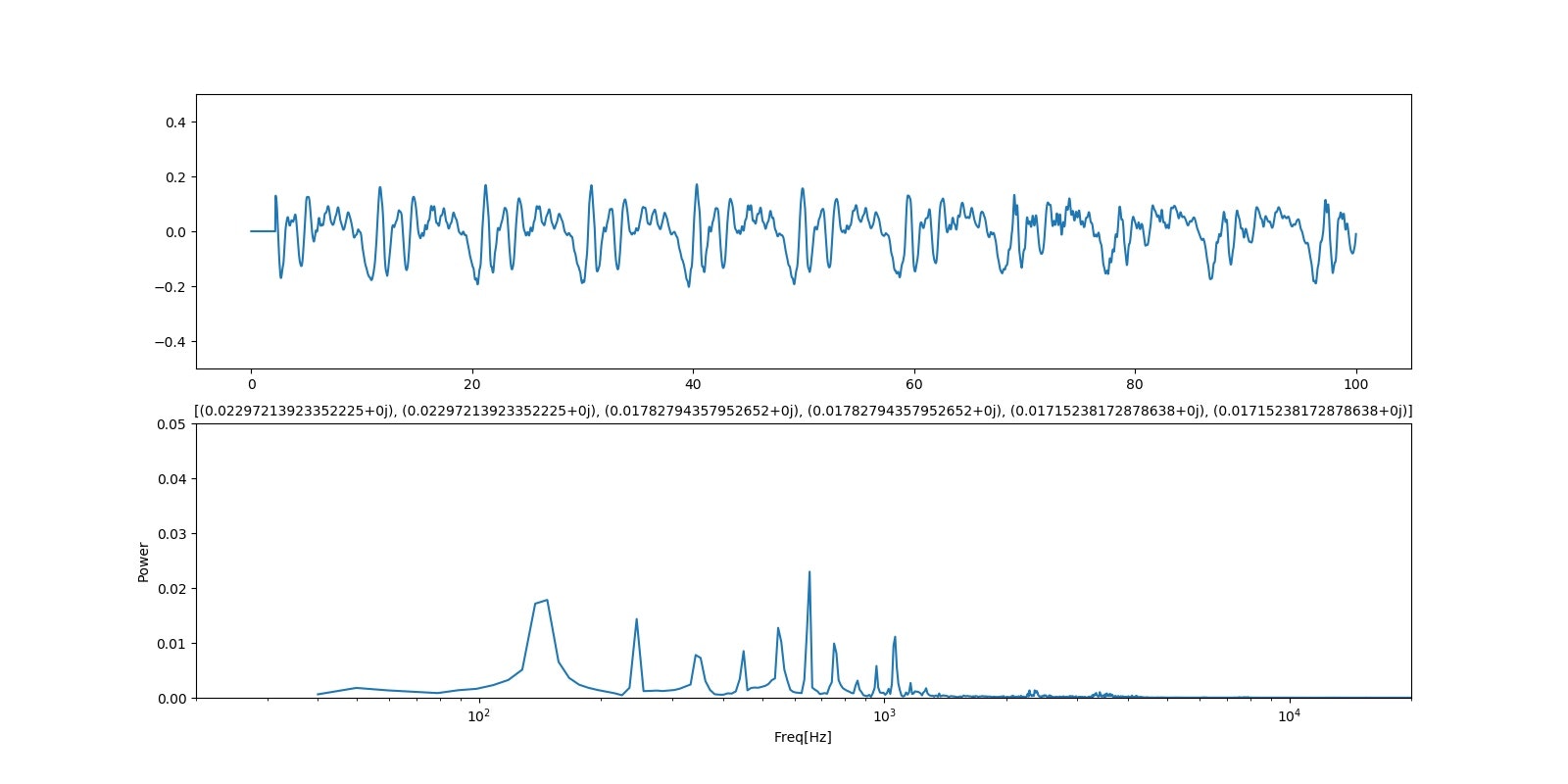
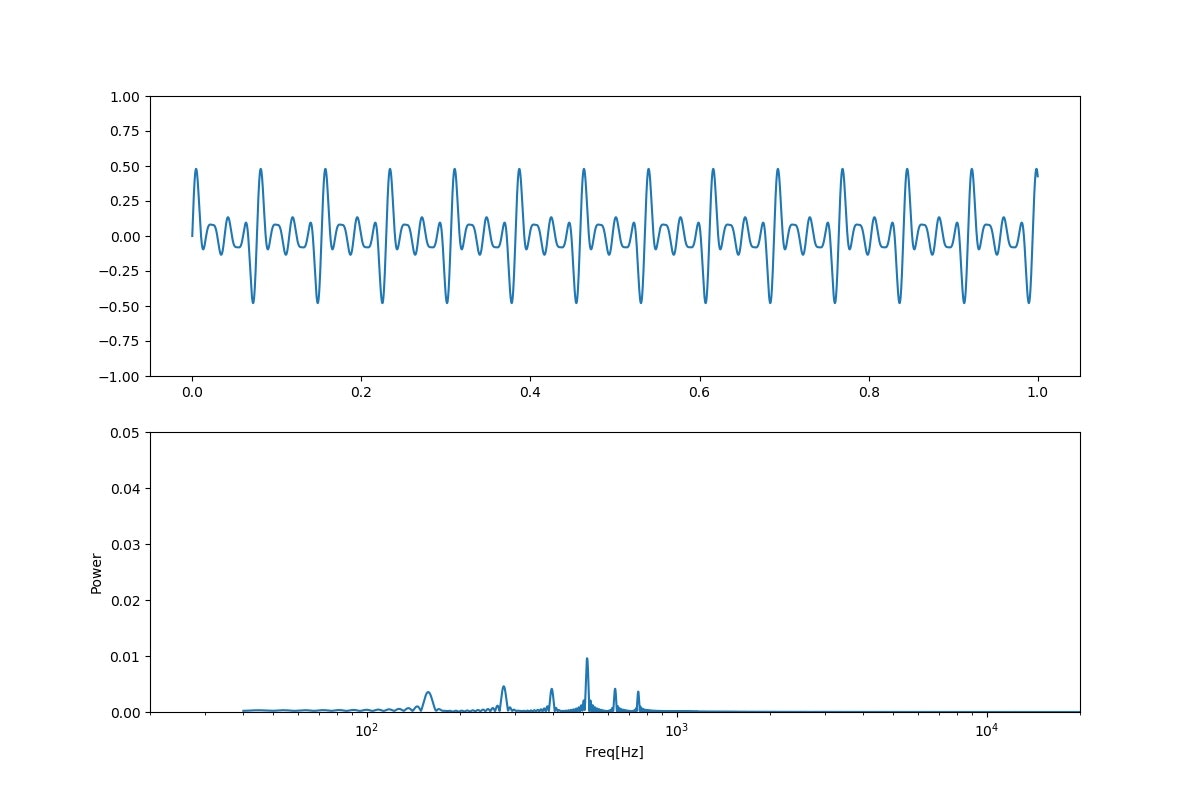
「あ；qiita、niconico」

「え；ウワン」

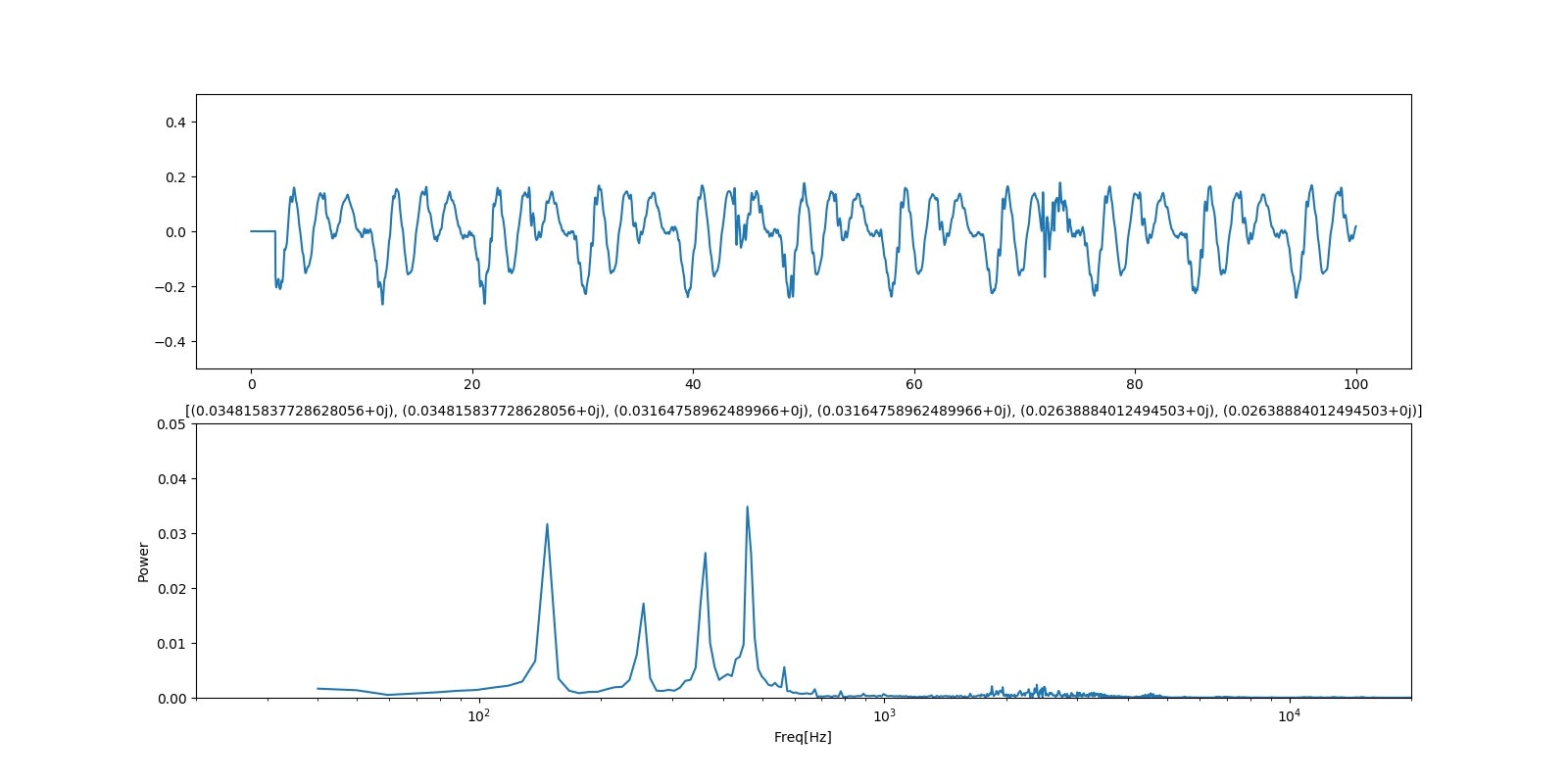
「え；qiita」

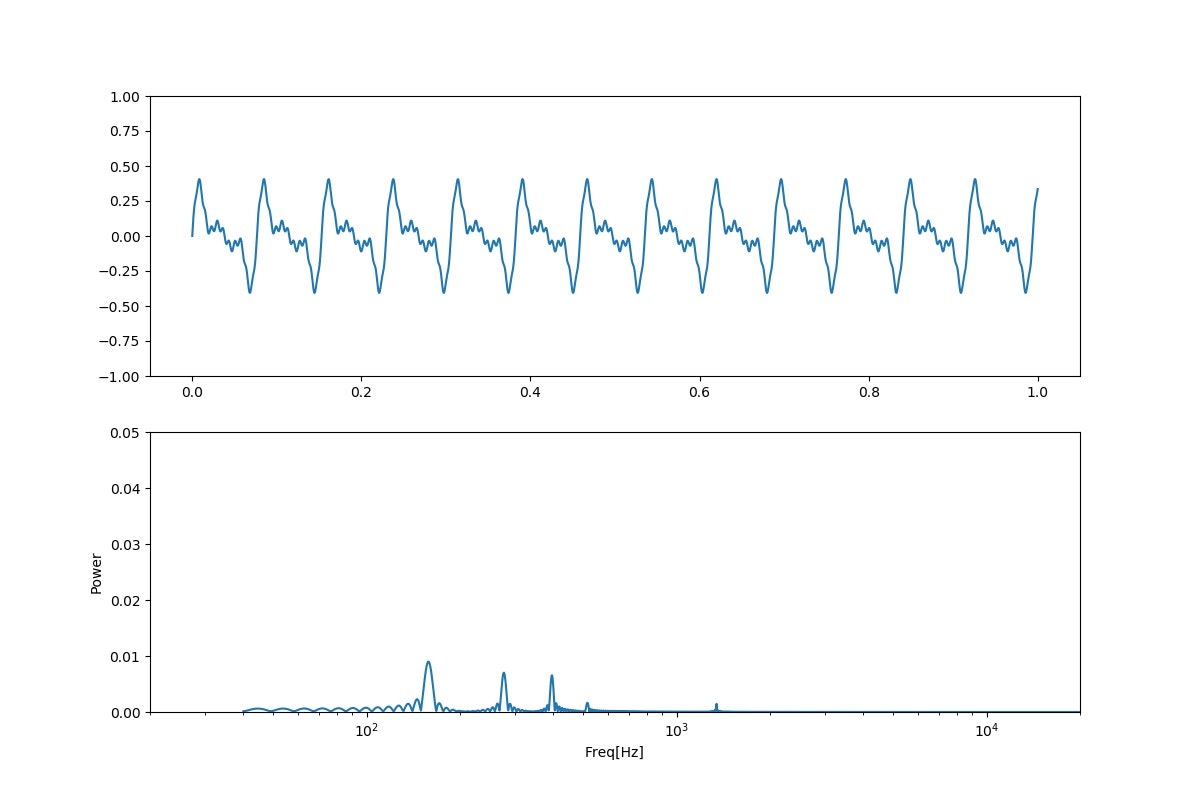
「え；niconico」

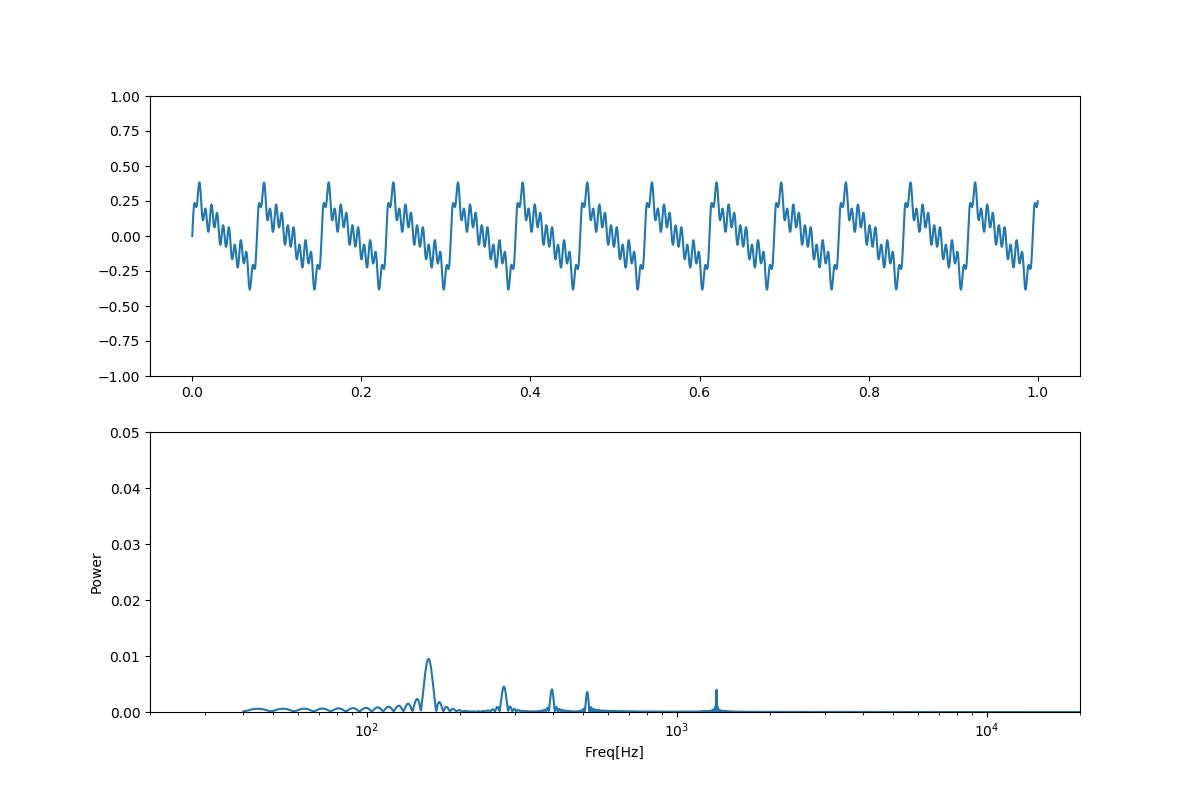
「い；ウワン」

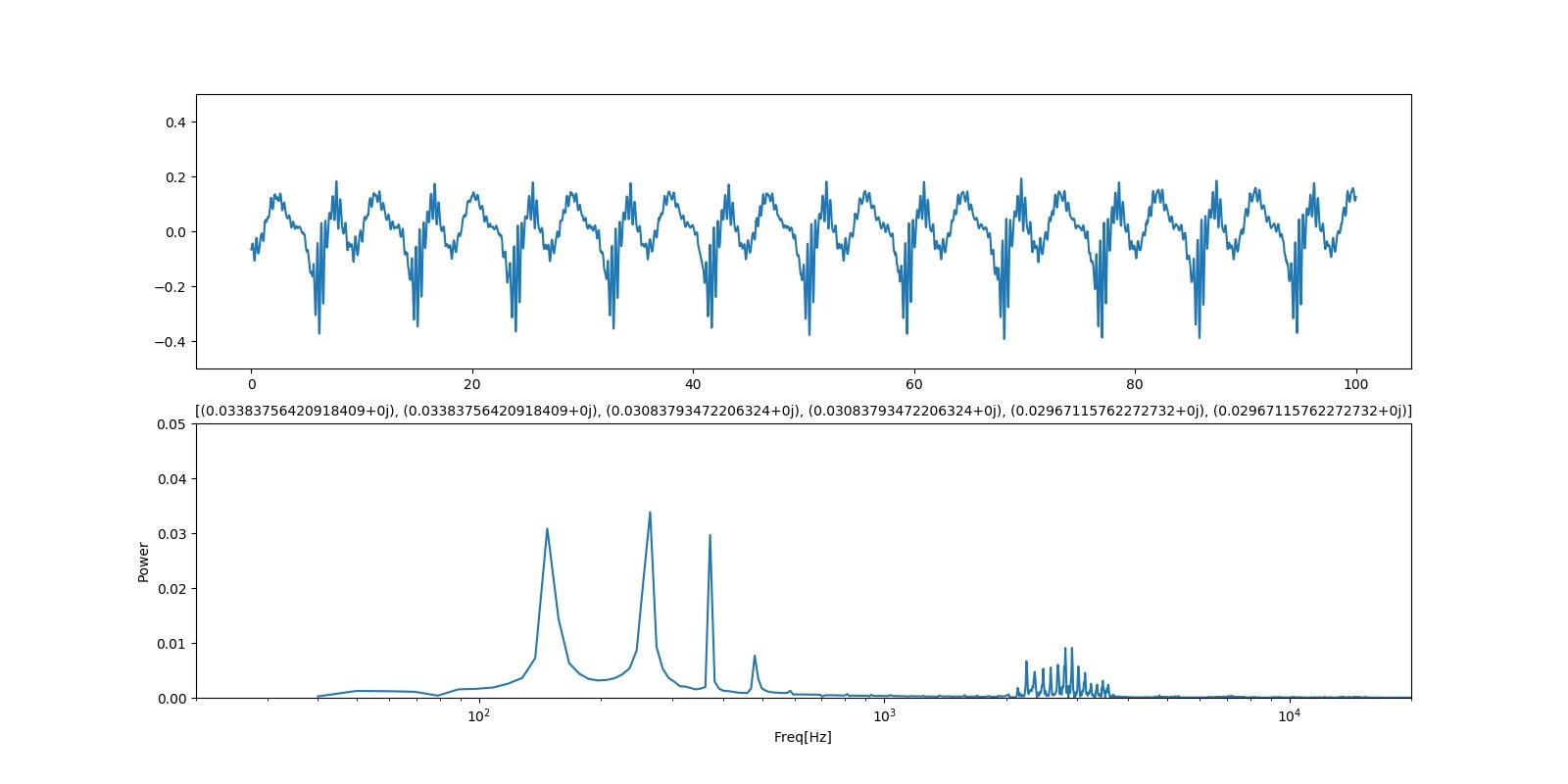
「い；qiita」

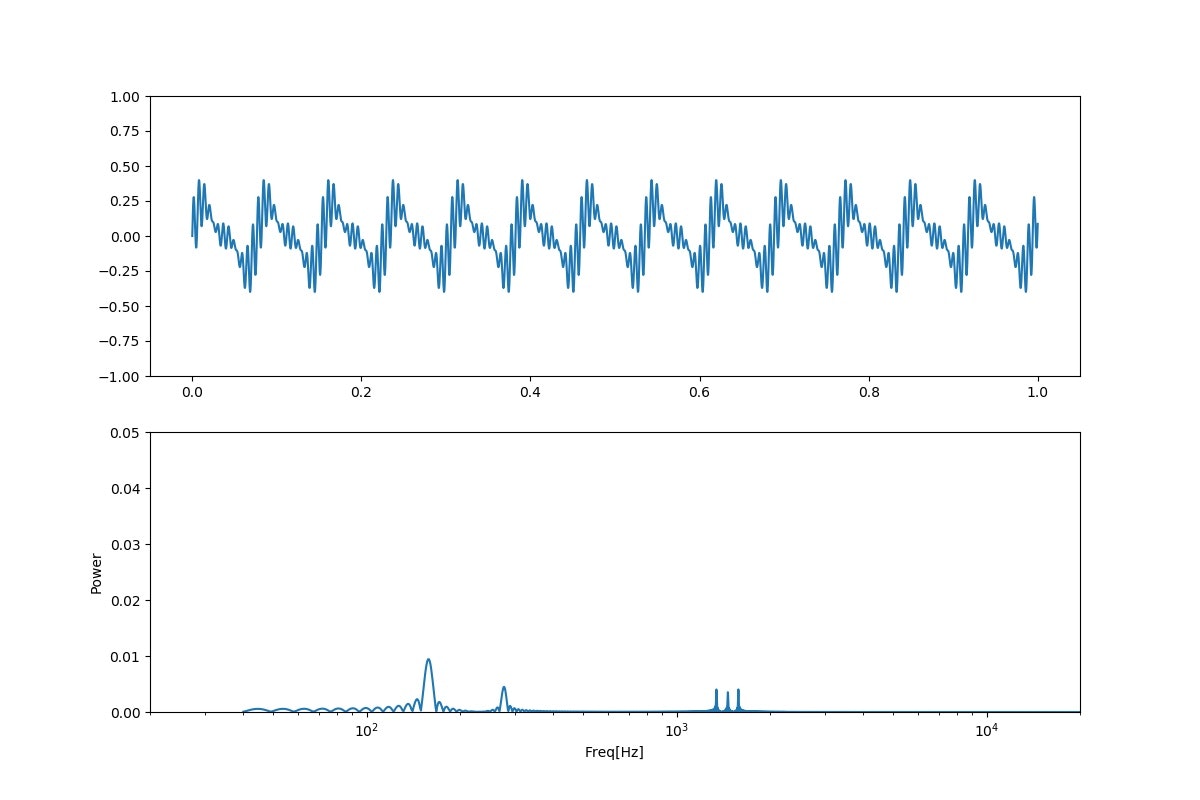
「い；niconico」

「お；ウワン」

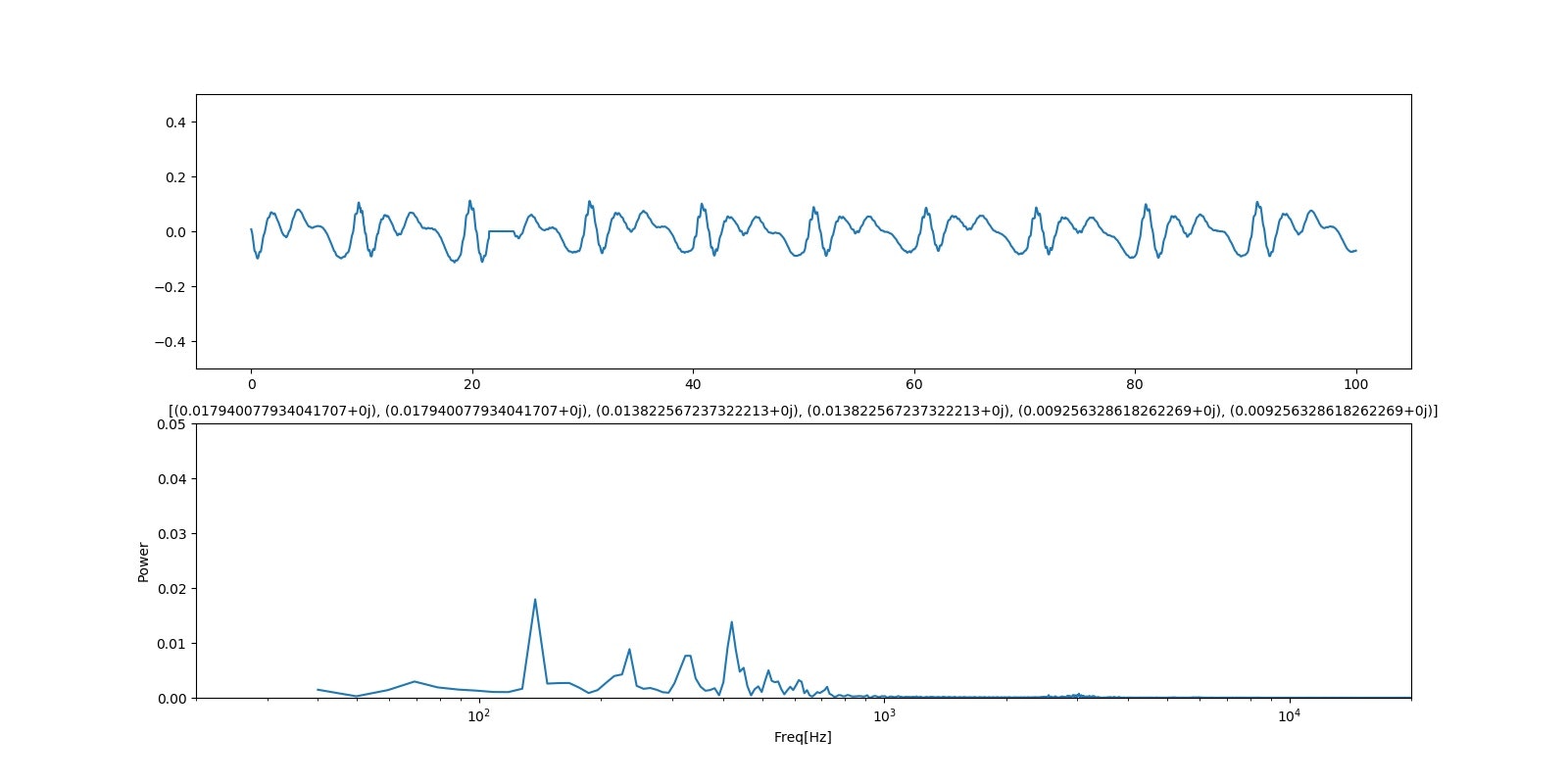
「お；qiita」

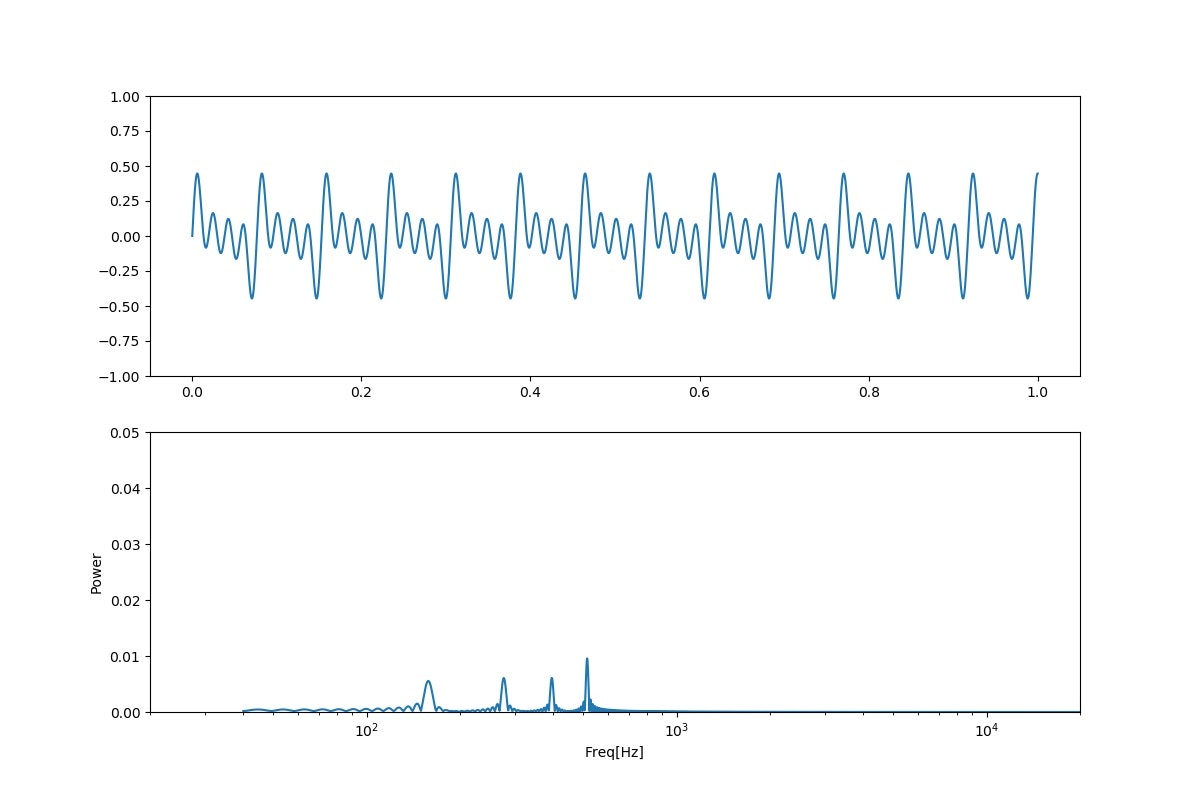
「お；niconico」

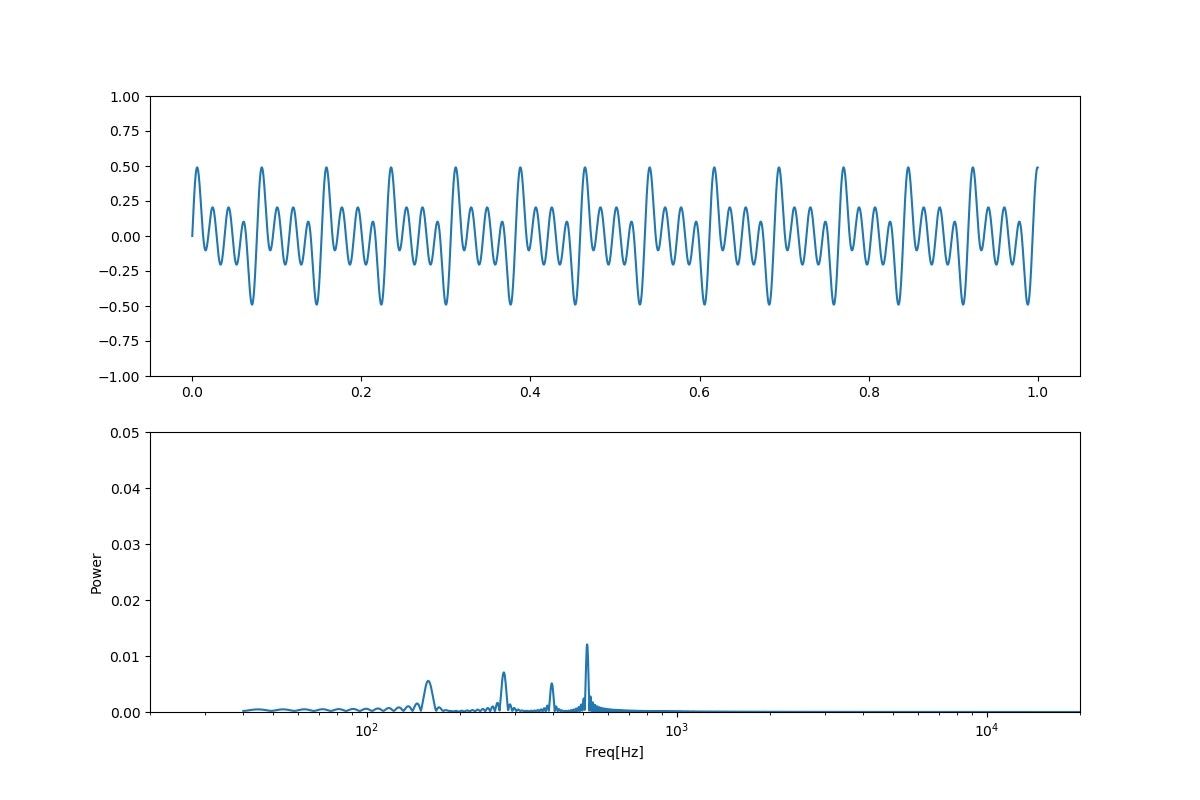
「う；ウワン」

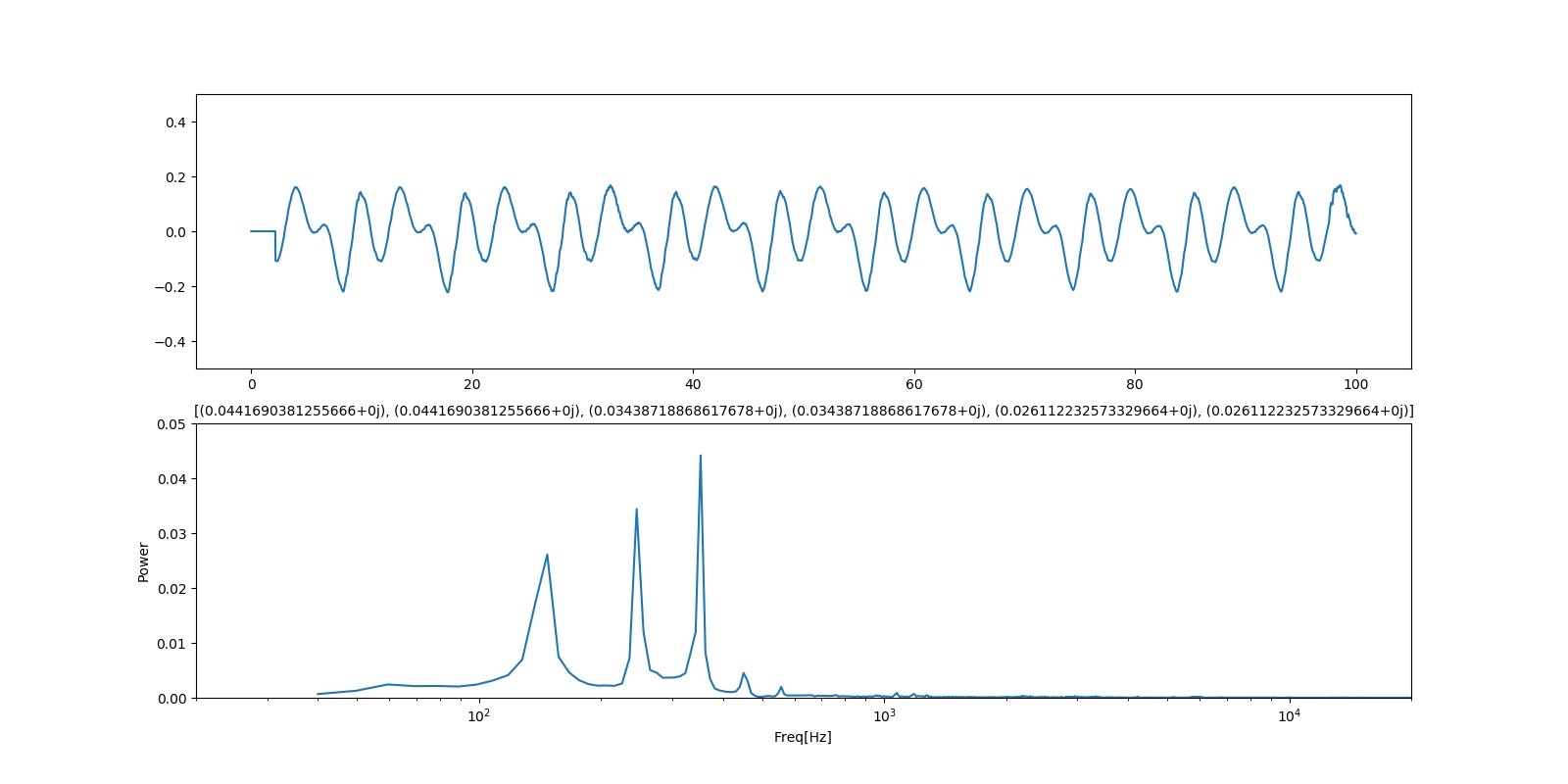
「う；qiita」

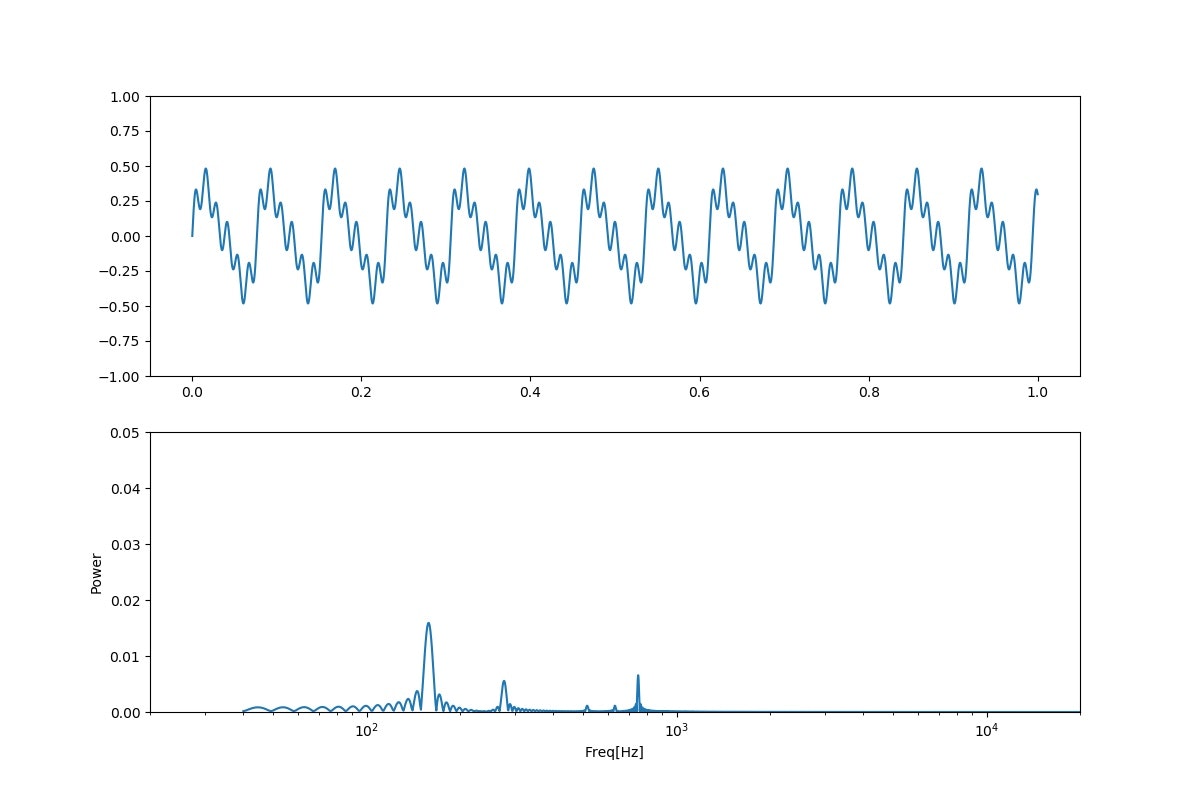
「う；niconico」

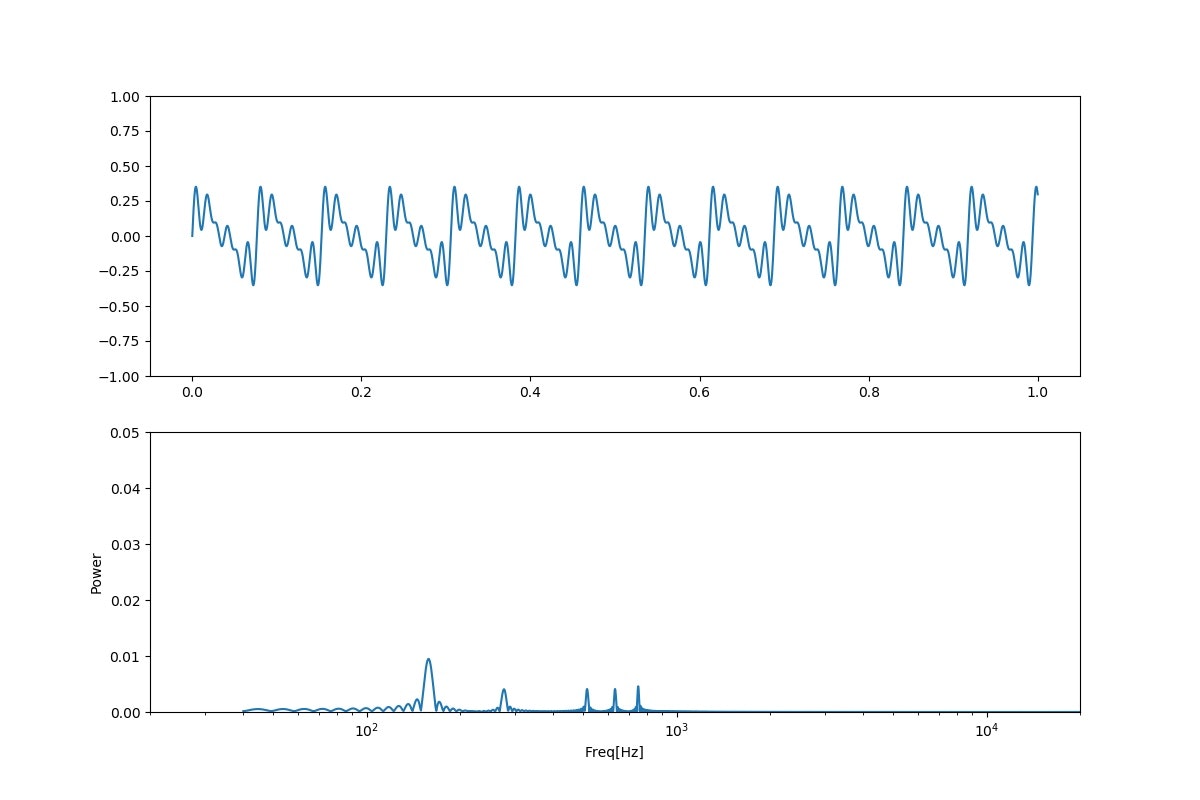
まとめ

・サイン波のフォルマント合成で母音を再現してみた
・聞いた感じでは、中間的な基準周波数では母音を再現しているというレベルであるが、低域・高周波領域ではちょっと母音には聞こえない
・音階にしたがって、周波数を変更して波形を見ると、一定波形が基準周波数と共に変化する

・現実のウワンの「あ、え、い、お、う」と比較すると、中間的な領域でさえもう一息な感じである
・現実な母音を再現しようと思う

おまけ

#https://www.nicovideo.jp/watch/sm13283644 niconico ここの周波数を使いました
#https://qiita.com/rild/items/339c5c36f4c1ad8d4325 qiita ここの周波数を使いました

import numpy as np
from matplotlib import pyplot as plt
import wave
import struct
import pyaudio
from scipy.fftpack import fft, ifft
import cv2

#パラメータ
RATE=44100
N=1
CHUNK=1024*N
p=pyaudio.PyAudio()
fn=RATE
nperseg=fn*N

stream=p.open(format = pyaudio.paInt16,
        channels = 1,
        rate = RATE,
        frames_per_buffer = CHUNK,
        input = True,
        output = True) # inputとoutputを同時にTrueにする

fs = RATE#サンプリング周波数
sec = 0.1 #秒
s='aiueo_'
sa='a'
def sin_wav(A,f0,fs,t):
    point = np.arange(0,fs*t)
    sin_wav =A* np.sin(2*np.pi*f0*point/fs)
    return sin_wav

def create_wave(A,f0,fs,t):#A:振幅,f0:基本周波数,fs:サンプリング周波数,再生時間[s]
    sin_wave=0
    print(A[0])
    int_f0=int(f0[0])
    for i in range(0,len(A),1):
        f1=f0[i]
        sw=sin_wav(A[i],f1,fs,t)
        sin_wave += sw
    sin_wave = [int(x * 32767.0) for x in sin_wave]    
    binwave = struct.pack("h" * len(sin_wave), *sin_wave)
    w = wave.Wave_write('./aiueo/'+s+'/'+sa+'/'+str(int_f0)+'Hz.wav')
    p = (1, 2, fs, len(binwave), 'NONE', 'not compressed')
    w.setparams(p)
    w.writeframes(binwave)
    w.close()

def sound_wave(fu):
    int_f0=int(fu)
    wavfile = './aiueo/'+s+'/'+sa+'/'+str(int_f0)+'Hz.wav'
    wr = wave.open(wavfile, "rb")
    input = wr.readframes(wr.getnframes())
    output = stream.write(input)
    sig =[]
    sig = np.frombuffer(input, dtype="int16")  /32768.0
    return sig

fig = plt.figure(figsize=(12, 8)) #...1
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
A=(0.07,0.09,0.08,0.19,0.08,0.07) #a
f0=27.5 #261.626
f=(f0,2*f0,3*f0,4*f0,5*f0,6*f0) #a

def B(a0=220):
    B=[]
    r= 1.059463094
    b=1
    for n in range(60):
        b *= r
        B.append(b*a0)
    return B

B=B(27.5)
sk=0

def skf(sk):
    skf=sk
    skf = skf+1
    skf=skf%60
    print(skf)
    f0=B[skf]
    return f0,skf

while True:
    create_wave(A, f, fs, sec)
    sig = sound_wave(f[0])
    #cv2.imshow('image',img)
    freq =fft(sig,int(fn))
    Pyy = np.sqrt(freq*freq.conj())/fn
    f = np.arange(20,20000,(20000-20)/int(fn))
    ax2.set_ylim(0,0.05)
    ax2.set_xlim(20,20000)
    ax2.set_xlabel('Freq[Hz]')
    ax2.set_ylabel('Power')
    ax2.set_xscale('log')
    ax2.plot(2*f*RATE/44100,Pyy)

    #ax2.set_axis_off()
    x = np.linspace(0, 1, sec*nperseg)
    ax1.plot(x,sig)
    ax1.set_ylim(-1,1)
    int_f0=int(f0)
    plt.savefig('./aiueo/'+s+'/'+sa+'/IntensityvsFreq_'+str(int_f0)+'.jpg')
    plt.clf()
    ax1 = fig.add_subplot(211)
    ax2 = fig.add_subplot(212)
    img=cv2.imread('./aiueo/'+s+'/'+sa+'/IntensityvsFreq_'+str(int_f0)+'.jpg')
    cv2.imshow('image',img)
    print("f0_{},A_{},B_{},C_{},D_{}".format(int_f0,A[0],A[1],A[2],A[3]))
    k = cv2.waitKey(0)
    if k == 27:         # wait for ESC key to exit
        cv2.destroyAllWindows()
        break
    elif k == ord('e'): # e 
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='e'
        #f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0,11*f0)
        A=(0.19,0.09,0.08,0.07,0.08) #qiita
        #A=(0.18,0.14,0.13,0.03,0.03) #niconico
    elif k == ord('c'):
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='e'
        #f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0,11*f0)
        A=(0.19,0.09,0.08,0.07,0.08) #qiita
        #A=(0.18,0.14,0.13,0.03,0.03) #niconico
    elif k == ord('a'): # a 
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='a'
        f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0,5*f0,6*f0)
        A=(0.07,0.09,0.08,0.19,0.08,0.07) #qiita
        #A=(0.07,0.09,0.08,0.19,0.08,0.07) #niconico
    elif k == ord('z'):
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='a'
        f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0,5*f0,6*f0) 
        A=(0.07,0.09,0.08,0.19,0.08,0.07)  #qiita
        #A=(0.07,0.09,0.08,0.19,0.08,0.07) #niconico
    elif k == ord('i'): # i
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='i'
        #f0,sk=skf(sk)
        f=(f0,2*f0,11*f0,12*f0,13*f0)
        A=(0.19,0.09,0.08,0.07,0.08)  #qiita
        #A=(0.52,0.03,0.02,0.01,0.02) #niconico
    elif k == ord('p'):
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='i'
        #f0,sk=skf(sk)
        f=(f0,2*f0,11*f0,12*f0,13*f0)
        A=(0.19,0.09,0.08,0.07,0.08) #qiita
        #A=(0.52,0.03,0.02,0.01,0.02) #niconico
    elif k == ord('o'): # o
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='o'
        #f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0)
        A=(0.11,0.12,0.12,0.19)  #qiita
        #A=(0.11,0.14,0.10,0.24) #niconico
    elif k == ord('r'):
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='o'
        #f0,sk=skf(sk)
        f=(f0,2*f0,3*f0,4*f0)
        A=(0.11,0.12,0.12,0.19)  #qiita
        #A=(0.11,0.14,0.10,0.24) #niconico
    elif k == ord('u'): # u
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='u'
        #f0,sk=skf(sk)
        f=(f0,2*f0,4*f0,5*f0,6*f0)
        A=(0.19,0.08,0.08,0.08,0.09) #qiita
        #A=(0.32,0.11,0.02,0.02,0.13) #niconico
    elif k == ord('t'):
        cv2.imwrite('./aiueo/'+s+'/'+sa+ '/f0_{}_{}_{}_{}_{}.jpg'.format(int_f0,A[0],A[1],A[2],A[3]),img)
        sa='u'
        #f0,sk=skf(sk)
        f=(f0,2*f0,4*f0,5*f0,6*f0)
        A=(0.19,0.08,0.08,0.08,0.09) #qiita
        #A=(0.32,0.11,0.02,0.02,0.13) #niconico