今朝の以下のデータで再計算してみたので結果を載せます。
なお、この記事の内容は素人が書いたものであり、責任は読んだ人の自己責任で判断してください。
理論を分かり易さのために加筆しました(4.12.2020)
データは以下の参考①から3つのファイル(time_series_covid19_confirmed_global.csv, time_series_covid19_deaths_global.csv, time_series_covid19_recovered_global.csv )をダウンロードして利用します。
一部、日本のデータは参考②のデータを読み取って、上記ファイルのconfirmedを書き換えます。
フランス領とイギリス領はデータがうまくいかないので3つのファイルから削除しています。
【データ取得】
①COVID-19/csse_covid_19_data/csse_covid_19_time_series
②データとグラフで見る新型コロナウイルス@日テレNEWS
・理論(できるだけ分かり易く)
以下のSIRモデルを利用しています。(導出は前出参照)
{\begin{align}
\frac{dS}{dt} &= -\gamma R I \\
\frac{dI}{dt} &= \gamma (R - 1) I \\
\frac{dr}{dt} &= \gamma I \\
\end{align}
}
これらの式の意味は、以下のとおり
第一方程式;翌日の未感染数$S$は現存感染数$I$の$\gamma R$倍ずつ減少する
第二方程式;翌日の感染数は現存感染数$I$の$\gamma (R-1)$倍ずつ増加する
第三方程式;翌日の治癒数(+死亡数+隔離数(今回0))は現存感染数$I$の$\gamma$倍ずつ増加する
すなわち、第二方程式の関係は第一方程式からの流入と第三方程式の流出の関係になっていることが分かる。
上記方程式において、現存感染数$I$と累計治癒数$r$が観測値であり、それらを使い数値微分$\frac{dI}{dt}, \frac{dr}{dt}$を利用することにより、
・第二方程式から$\gamma (R-1)$
・第三方程式から$\gamma$
が求められ、その結果、$\gamma$と$R$が求められる。
また、医療崩壊と関連するパラメータ現存感染数$I$とremoved(=快復数+死亡数)$r$との比
\frac{I}{r+D}
を計算しています。(グラフ内では$\frac{I}{R+D}$と記載)
治癒数が増加し1以下になると、それ以上現存感染数が増えないので医療崩壊は免れることになります。
逆に大きいままだといずれ医療崩壊が発生し、治癒数が減少し増加に転じてしまいます。
ただし、死亡数(又は死亡率、これらは測定値)が増加する場合もこの指標は減少しますが、そのときも医療崩壊であり注意が必要です。
したがって、この方程式の係数の意味として
・$\gamma$は医療施設や医療体制とウィルスの性質に依存した係数
・$R$は実効再生産数と呼ばれ、これはいわゆる行動変革(変容)で小さくできる係数
だと言えます。
なお、変数は以下の関係としている。
$R$;実効再生産数との混同を避けるためremoved(=快復数+死亡数+隔離数)を小文字にしている。
{\begin{align}
R &= R_0 \frac{S}{N}\\
R_0 &= \frac{\beta}{\gamma} \\
\end{align}
}
また、上記3つのファイルはそれぞれ
累計感染数 = time_series_covid19_confirmed_global.csv
治癒数 = time_series_covid19_recovered_global.csv
死亡数 = time_series_covid19_deaths_global.csv
です。
日々、これを計算すればそれぞれの日々の$\gamma$, $R$を求められます。
・コードは以下に置きました
(更新;上記理論で導出;結果は変わらず、計算日ー10日でフィッティングに変更)(4.13.2020)
・collective_particles/fitting_gamma_R_II.py
(更新前;gamma*(R-1)で導出)
・collective_particles/fitting_gamma_R.py
やったこと;各国のグラフ
・日本
・世界
・アメリカ
・イタリア、スペイン、フランス、スイス
・韓国、イラン
・武漢、北京、香港、台湾
・インド
・日本
現存感染数(上図赤プロット)が3月下旬にいきなり傾きが変わり感染拡大が加速しました。
上記の実効再生産数R_estが増加し$\gamma (R-1)$が高い数字で推移していて危険領域に入りました。
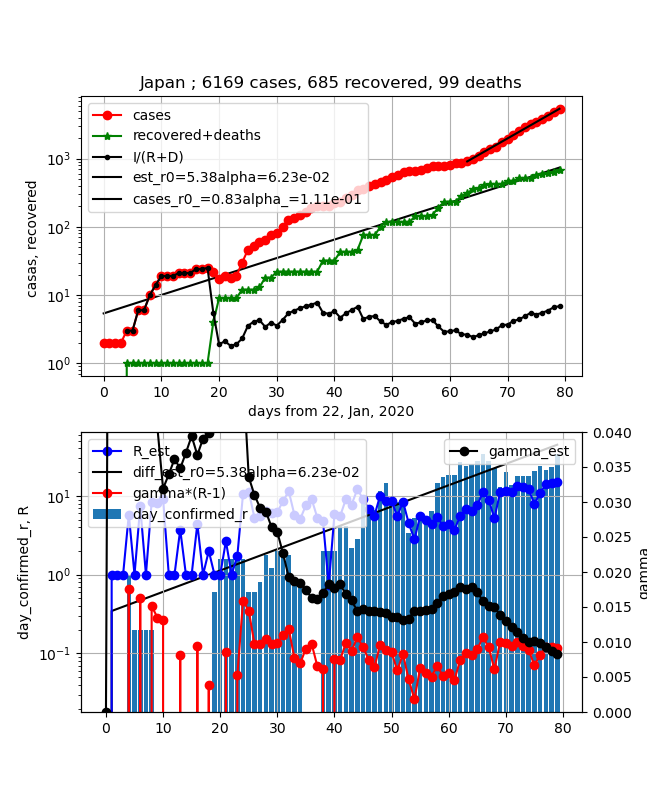
特徴
①上図赤プロット;拡大継続でほぼ直線上
②上図緑プロット;治雄数上昇率低いまま⇒感染拡大前の感染者治癒⇒予測;このあと拡大期の感染者治癒
③上図黒プロットI/(R+D);感染拡大で悪化中⇒予測;このあとピークになり減少する
④下図青プロットR;実効再生産数が10を超えて15位の大きな値
しかし、$\gamma (R-1)$のグラフは以下のとおり
前回、単調に増加していたが、ここで平坦になり減少してきたので感染拡大が収まる兆候!
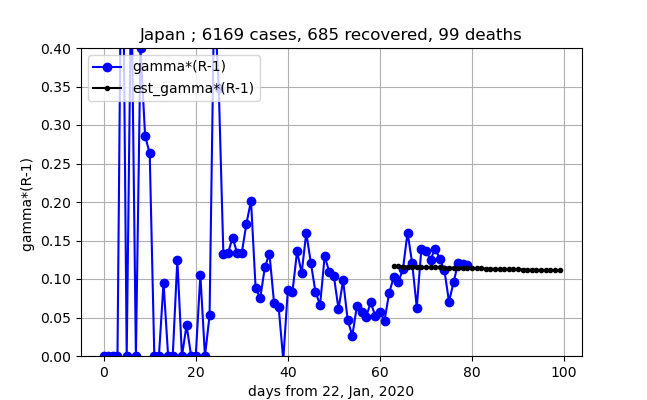
・世界
現存感染数は増加傾向にありますが、$\gamma (R-1)$が減少段階に入り感染数ピークが見える可能性が高まりました。
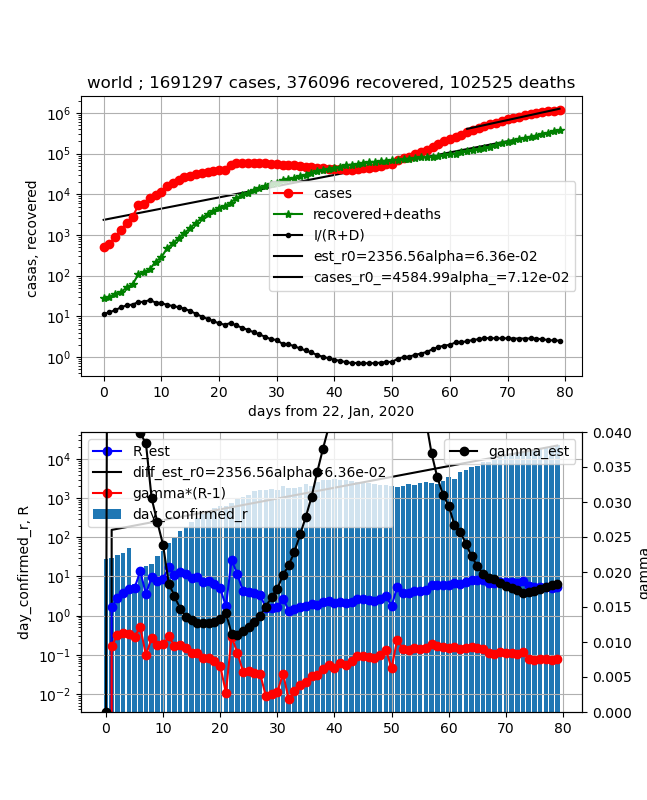
①上図赤プロット;増加傾向が鈍ってきた
②上図緑プロット;単調に増加
③上図黒プロットI/(R+D);①を反映して減少に転じてきた
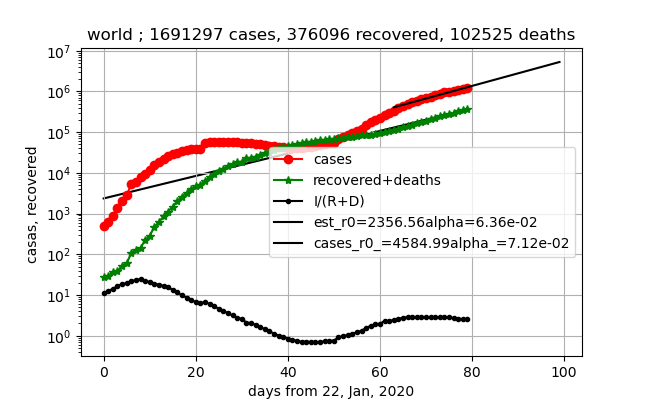
④現存感染者数は単調増加の予測直線の傾きが小さくなり、これと比較して鈍ってきた。
1000万人までは行かない状況
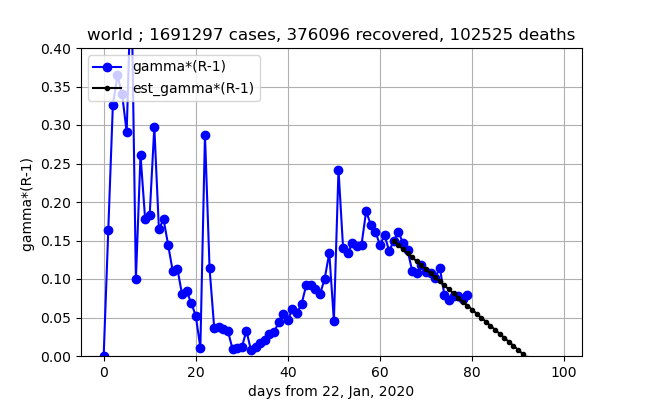
⑤上記グラフより、$\gamma (R-1)$の減少傾向継続しており、あと約11日で現存感染者数がピークになる。このグラフは2回連続で週ごとに下がっており、今週どうなるか興味深い。
・アメリカ
世界の傾向と同様に、現存感染数は増加傾向にありますが飽和が見え始め、$\gamma (R-1)$が減少段階に入り感染数ピークが見える可能性が高まりました。
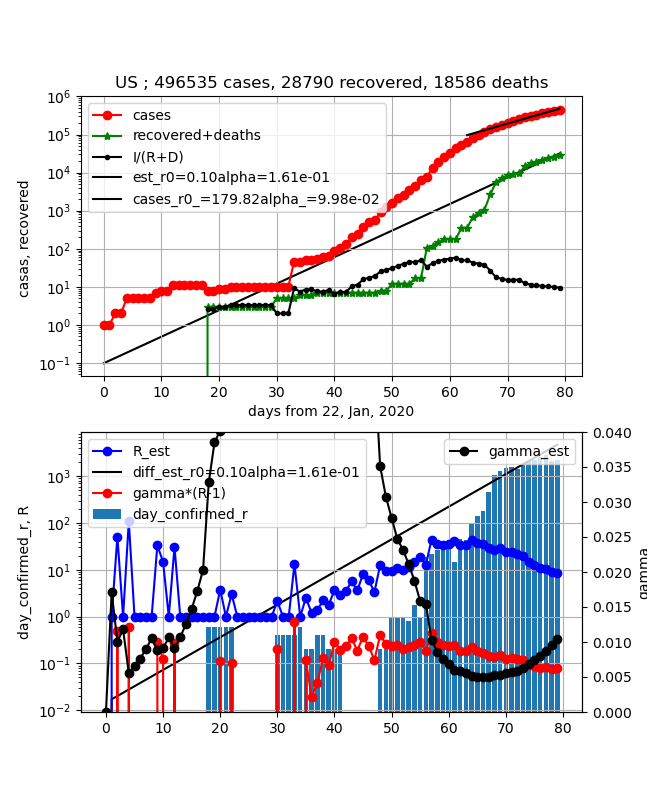
もうすぐ累計感染数が50万人だが、データは安定しており、管理されているように見える。
①上図赤プロット;増加傾向が鈍っている
②上図緑プロット;増加傾向だが鈍ってきたようだ
③上図黒プロットI/(R+D);ゆっくり減少傾向だがまだまだ治癒数が少ない
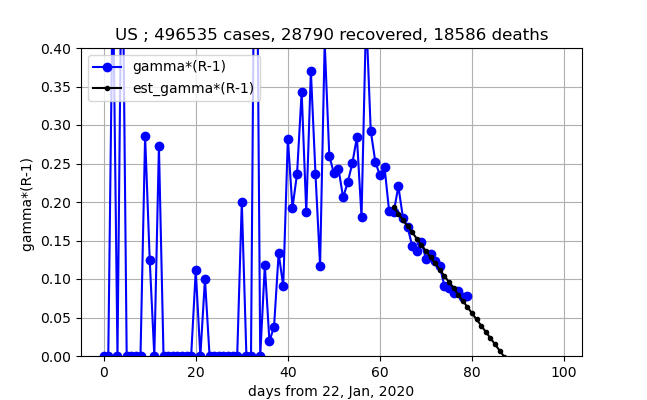
④もうすぐ感染数ピークになりそう。しかし、この予測直線だとあと1週間という予測と20日後という二つの直線が引けるのでこの期間に感染数ピークになると思われる。
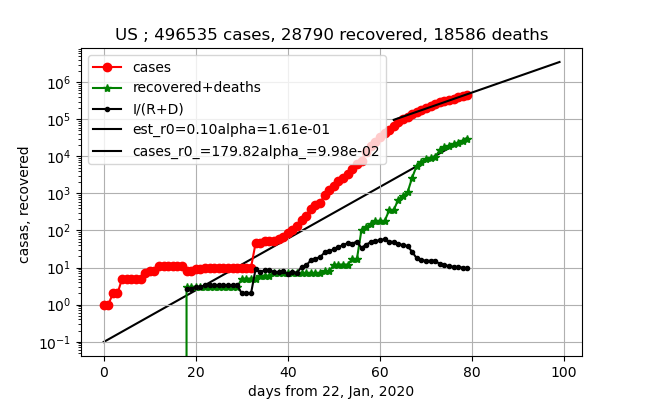
⑤上図だと、上記の最短の感染数ピークだとしても、現存感染数100万人までは行ってしまいそうな勢いである
・イタリア、スペイン、フランス、スイス、ドイツ
ヨーロッパ各国はロックダウンの効果が見え始め、ほぼ感染数ピークになりつつあるが、$\gamma (R-1)$が停滞気味で終息には予断を許さない状況
ロックダウンの時期(Twitterより);3月20日前後(イタリア北部3/8、スペイン3/14、ドイツ3/16、フランス3/17)
・イタリア
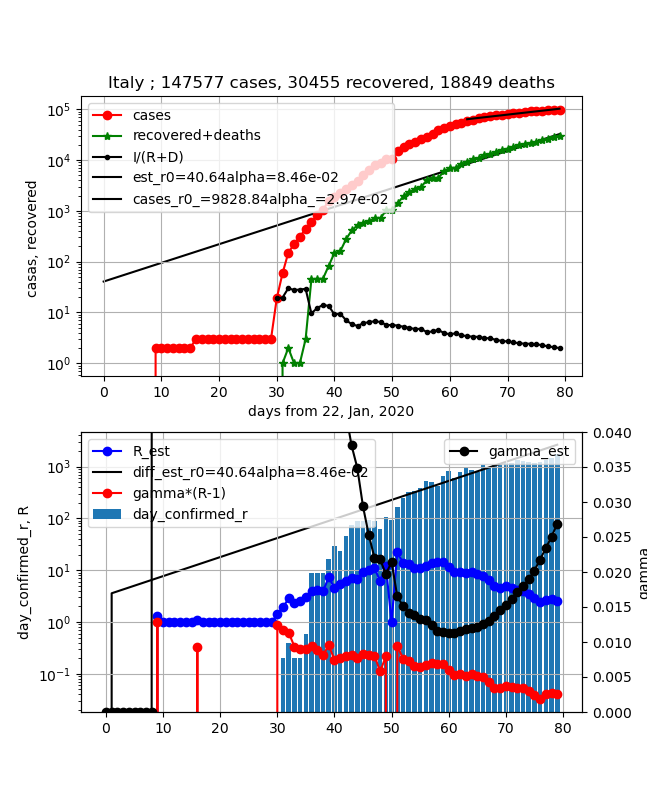
①上図赤プロット;ほぼフラットになった
②上図緑プロット;順調に増加
③上図黒プロットI/(R+D);安定して直線的に減少しているが、傾きが小さいので時間かかる
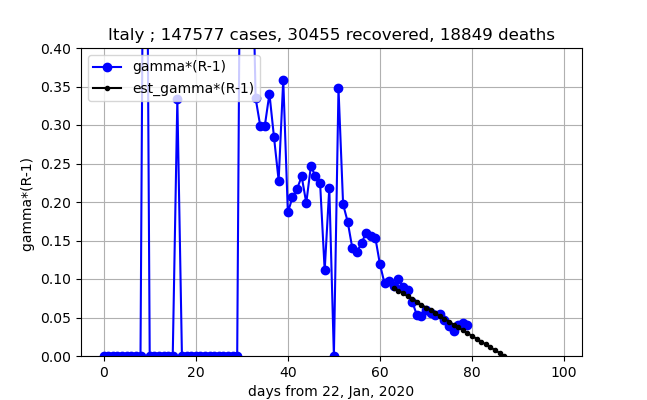
④順調に減少しているようだが、ここへ来て横に並んでいるのですこし鈍るかもしれない。このまま減少し続ければあと1週間で現存感染数ピークになる。予断は許さない状況。
・スペイン
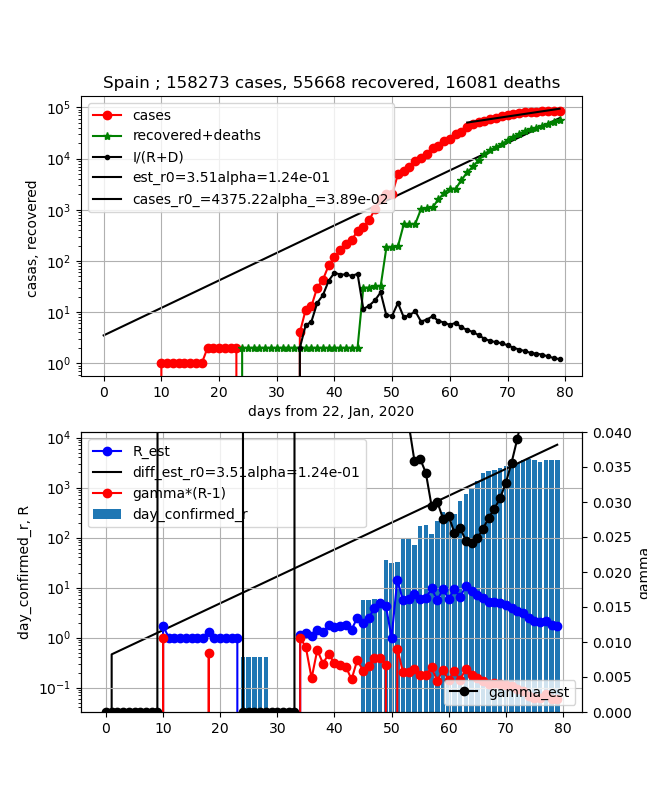
①上図赤プロット;飽和した。これから減少に転ずるところ
②上図緑プロット;直線的に増加して、現存感染数とほぼ同じ程度まで回復した
③上図黒プロットI/(R+D);上記を反映して直線的に1に近づいてほぼ1まで来た
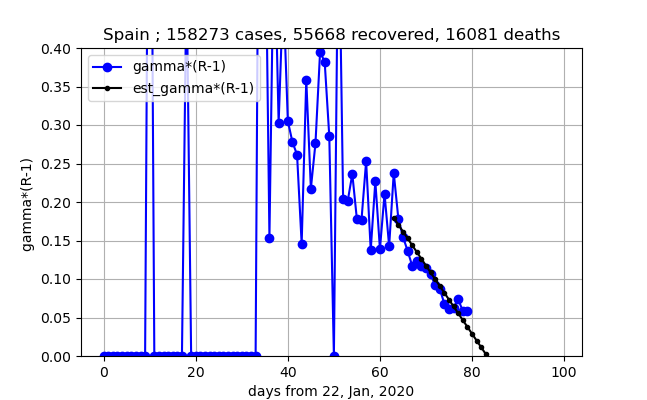
④ところがこの図は$\gamma (R-1)$が0.05手前で下げが鈍くなっていることを示しており、予断は許さない状況となっている。問題なければ3-4日で感染数ピークとなる。
・フランス
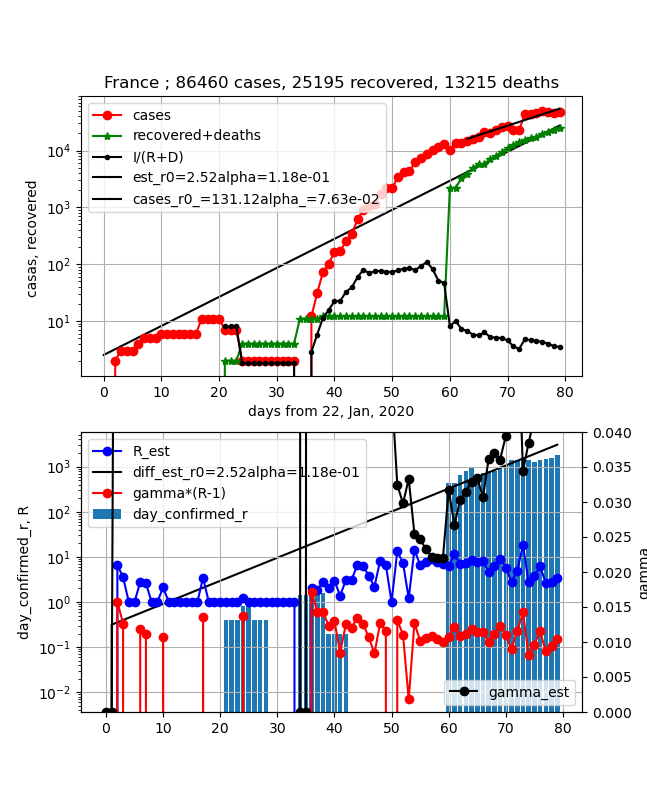
①上図赤プロット;一応ピークになっているようだが、データがあれているのでちょっと心配
②上図緑プロット;順調に増加傾向でもうすぐ現存感染数と同じような値になりそう
③上図黒プロットI/(R+D);減少傾向だが、傾きが小さいので医療機関は大変な状況が続きそう
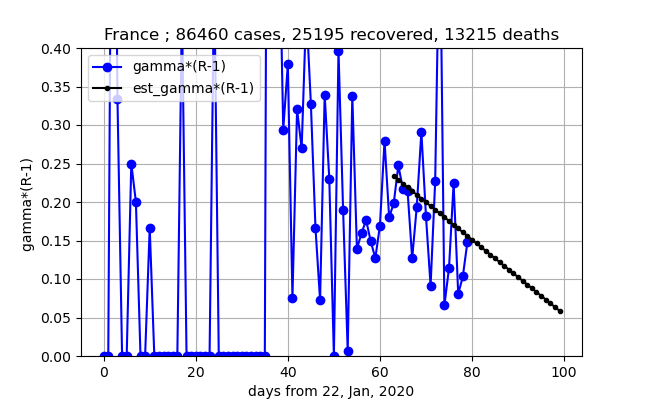
④データが荒れているのでなんとも言えない。
一応減少傾向が出ておりほんとの感染数ピークは20日以上かかりそう
・スイス
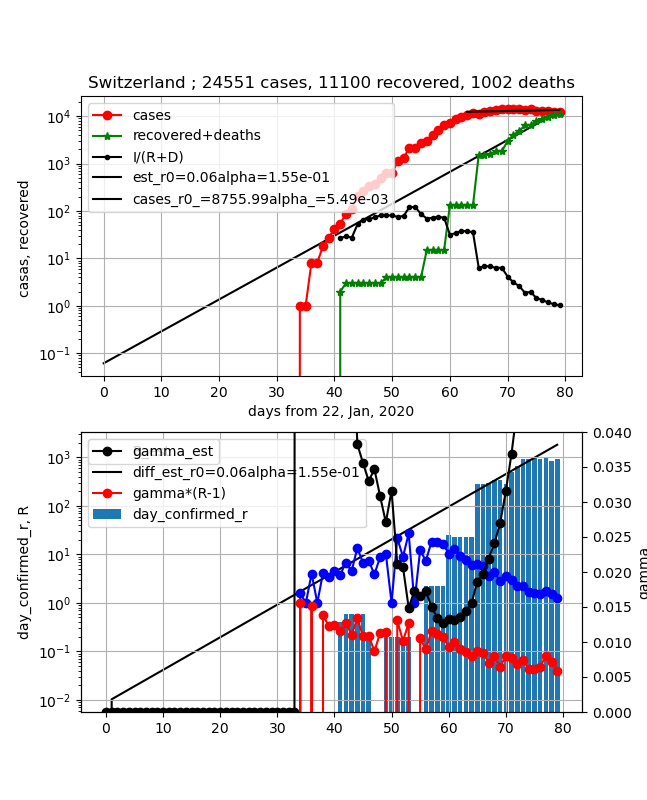
①上図赤プロット;感染数ピークになったように見えるが減少が極めて遅い
②上図緑プロット;順調に増加して感染数と同程度の値になったが増加が鈍った
③上図黒プロットI/(R+D);1の手前で傾きは小さくなったがだいたい1になった。まだまだ予断を許さない
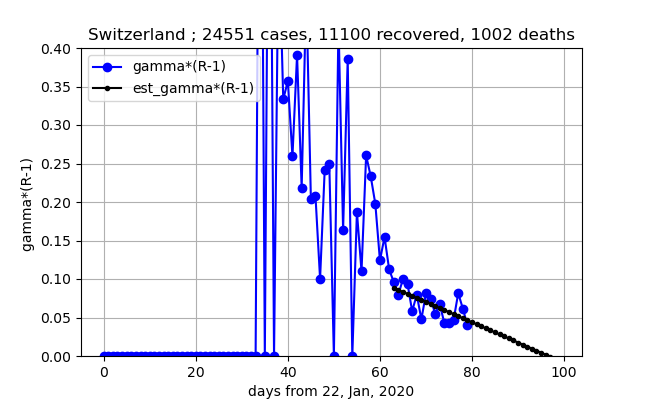
④やはりまだまだ終息には時間がかかるようだ。まだまだ予断を許さない状況。
・ドイツ
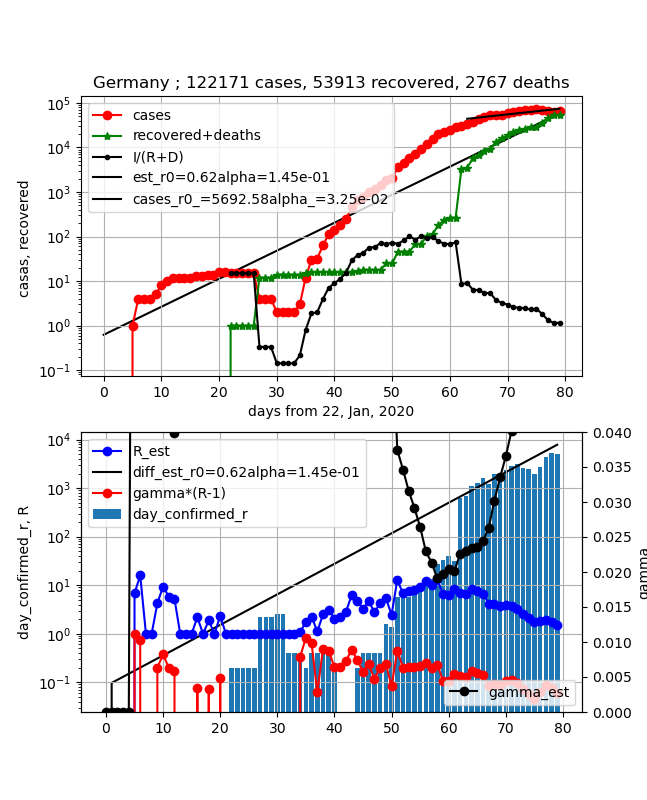
①上図赤プロット;スイスと似たような振る舞いで感染数ピークを越えた
②上図緑プロット;グネグネしているが、感染数ピークと同じような値にたどり着いたが増加が鈍った
③上図黒プロットI/(R+D);スイスと同様、1の手前で傾きが小さくなったがだいたい1になった。まだまだ予断を許さない
④下図青プロット;実効再生産数=1まであと少し、なのでもう少しで終息に向かいそう
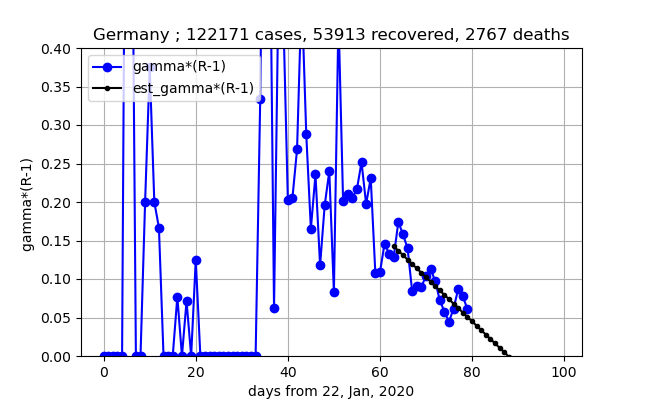
⑤スイスと同様で、やはりまだまだ終息には1週間程度かかるようだ、まだまだ予断を許さない状況
・韓国、イラン
感染数ピークには達したがその後の様子も厳しい状況
・韓国
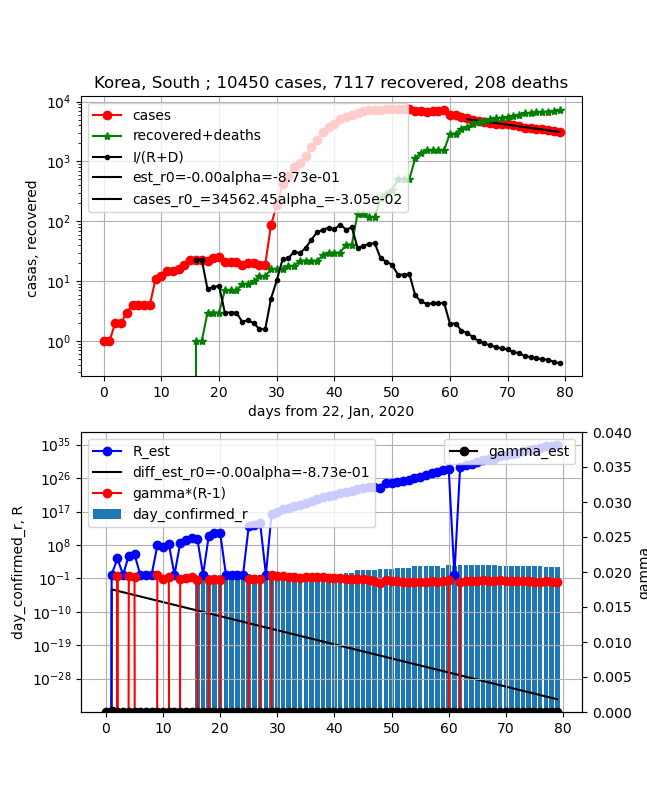
①上図赤プロット;感染数ピーク後の様子だが、だらだら下がっておりかなり長期化しそう
②上図緑プロット;治癒数も飽和しつつあり、なかなか100%の治癒にならない
③上図黒プロットI/(R+D);1以下になって下に凸で急激に減少するのかと思ったがだらだら減少です。つまり、なかなか治癒しないことを意味します。
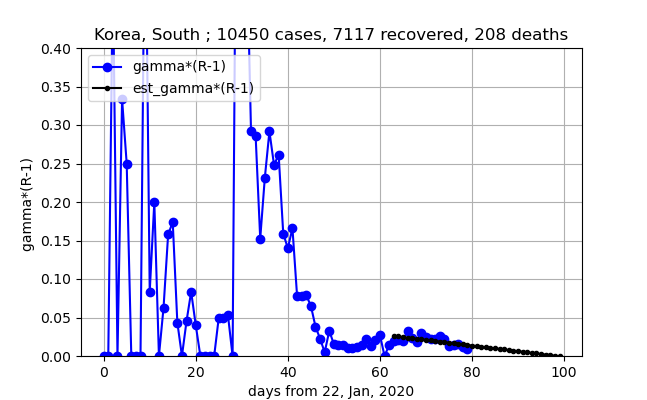
④上図は$\gamma (R-1)$がいつまでも0にならず、以前感染が発生していることを意味します。やはり世界が終息しないと終息できないのかもです。
・イラン
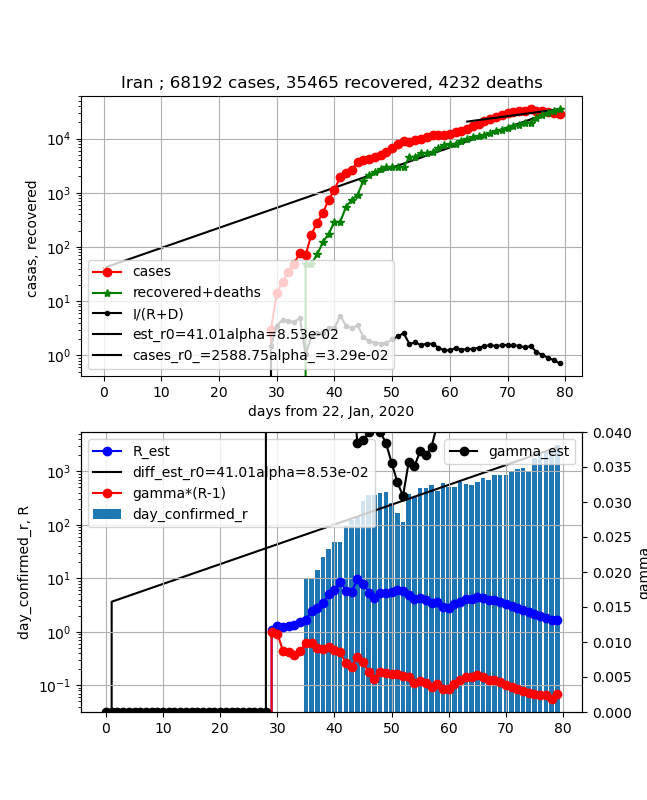
①上図赤プロット;感染数ピークを超えました
②上図緑プロット;韓国と同様感染数ピークとクロスしました
③上図黒プロットI/(R+D);4日程前に1以下になりいよいよ終息に向かいます
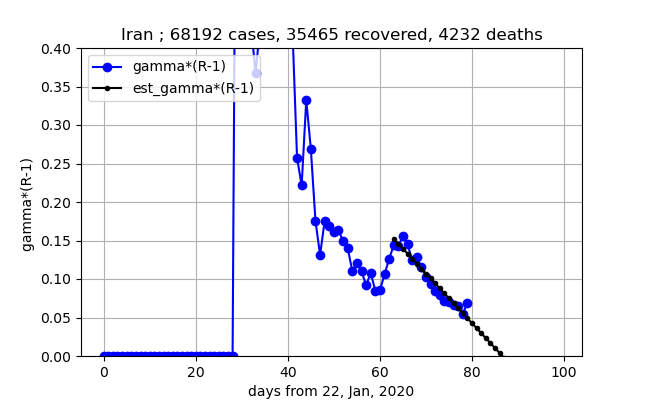
④上図は$\gamma (R-1)$は0以下になっておらず、まだまだ予断を許さない状況だということを示しています。
・武漢、北京、香港、台湾
中国は終息したと言われていますが、実態はどうでしょう
・武漢
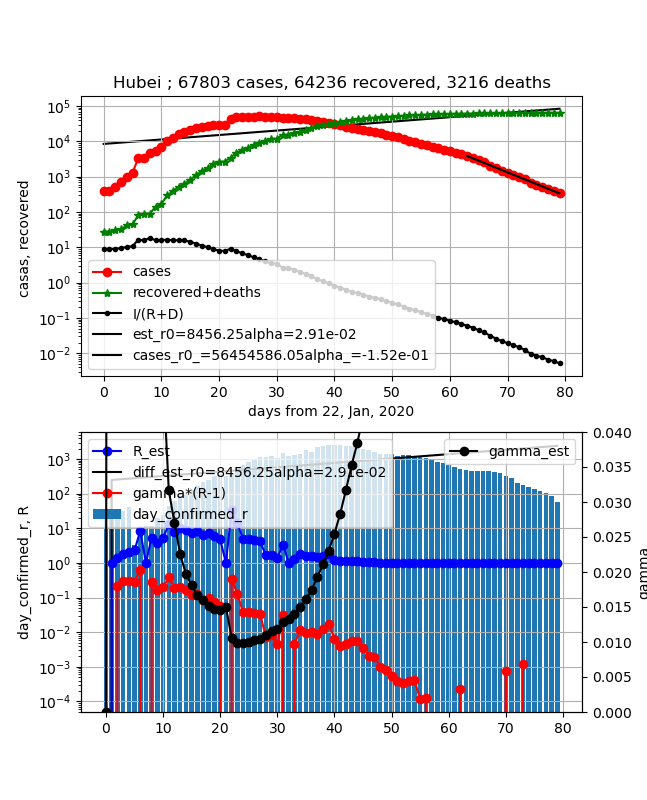
①上図赤プロット;かなりの人が退院しましたが、まだまだ数百人の人が現存感染者として残っています
②上図緑プロット;全体としてはほぼ水平になり、飽和したと言えます。
③上図黒プロットI/(R+D);$5x10^{-3}$程度まで減少しました
④下図青プロット;実効再生産数=1で感染が止まったことを意味しています
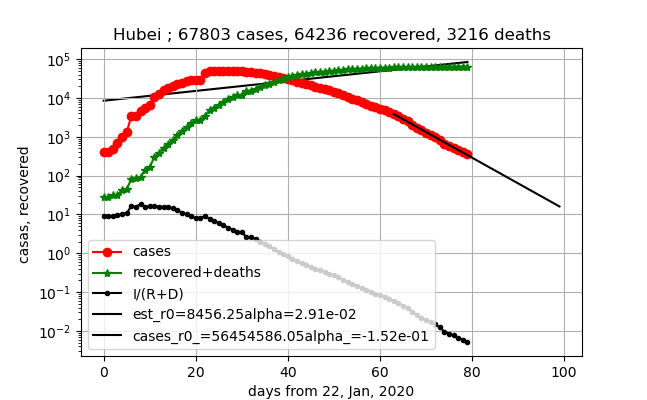
⑤現存感染数はまだまだ1月は残りそうです
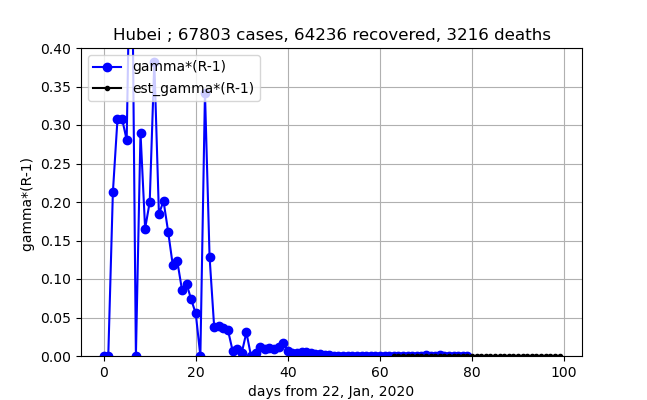
⑥上記の$R$の振る舞いで想像できますが、$\gamma (R-1)$は負になると思っていましたがそうはならず、すごいテイルを引いてやっと0になりました
・北京
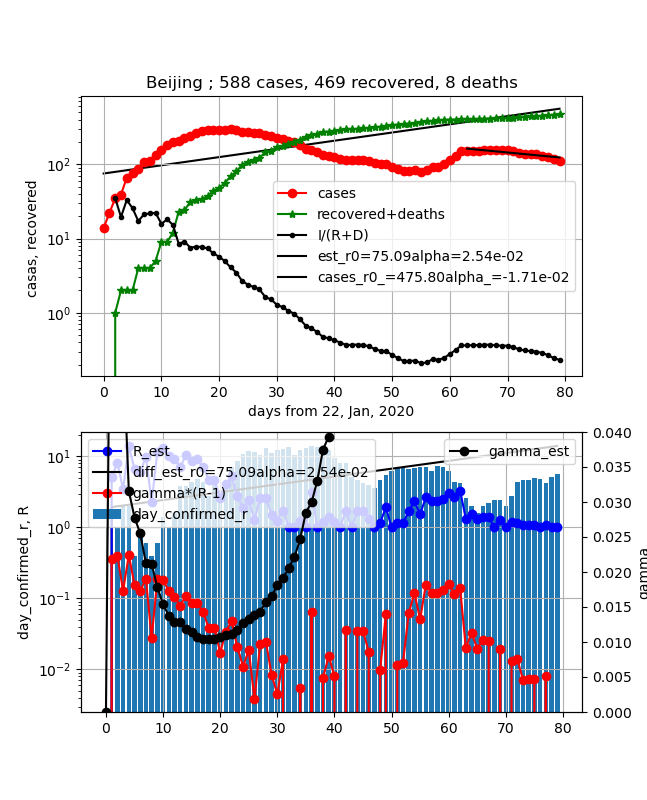
①上図赤プロット;一度感染数ピークとなりましたが世界の動向とどもに二度目のピークとなっています。それも10日前から減少が始まりました。
②上図緑プロット;第二波の感染者が治癒して上昇に転じました。
③上図黒プロットI/(R+D);第一波の大きな数字に隠れていますが、感染数曲線と同様な増加減少となっています。
④下図青プロット;実効再生産数がここへ来て1になりつつあります。ほぼ終息と言えます
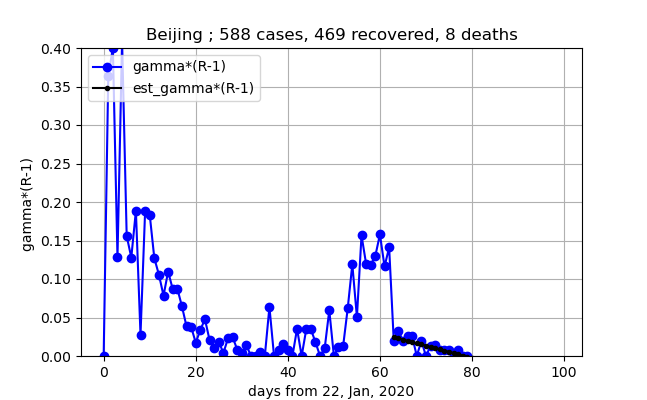
⑤④の傾向と同じでやっと$\gamma (R-1)=0$となりました
・香港
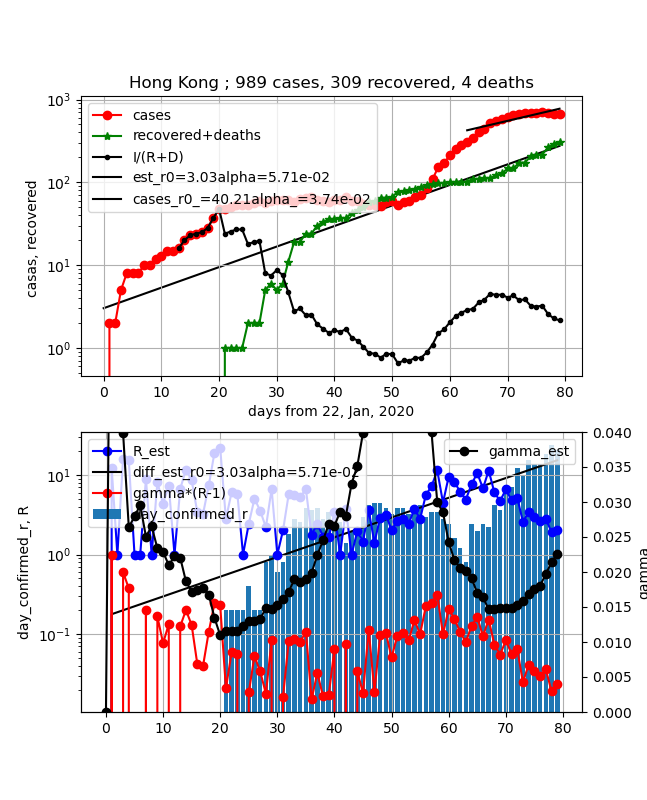
①上図赤プロット;香港は世界と同じ動向です。やっと感染数ピークを超えました
②上図緑プロット;直線的に増加しています。もうすぐ感染数と交差します
③上図黒プロットI/(R+D);1には程遠いですが、下降を始めました
④下図青プロット;実効再生産数は現在2位であり減少傾向で、もうすぐ1になりそうです
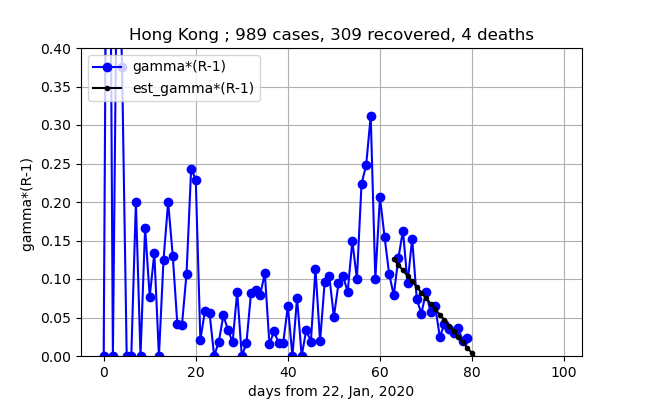
・インド
人口多く、実効再生産数が10以上で、拡大期であり注視が必要。
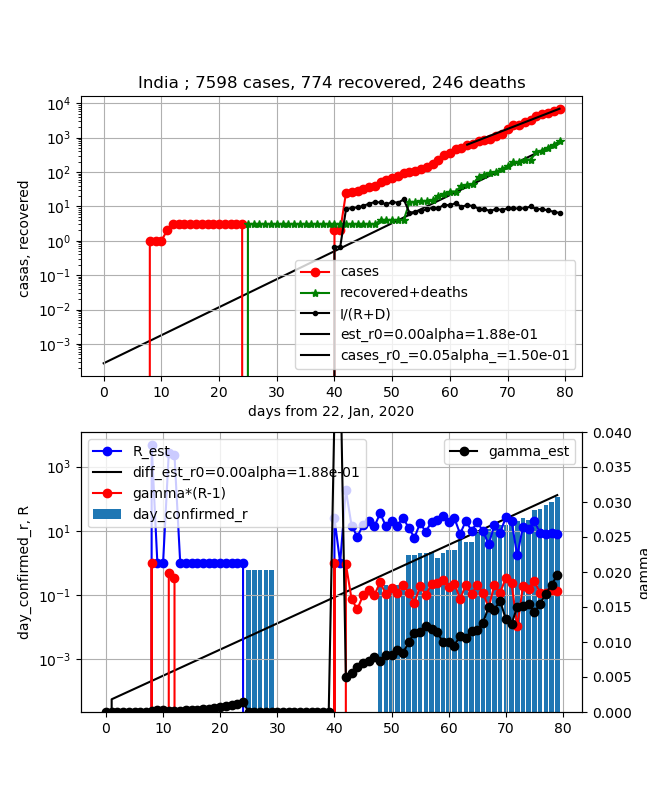
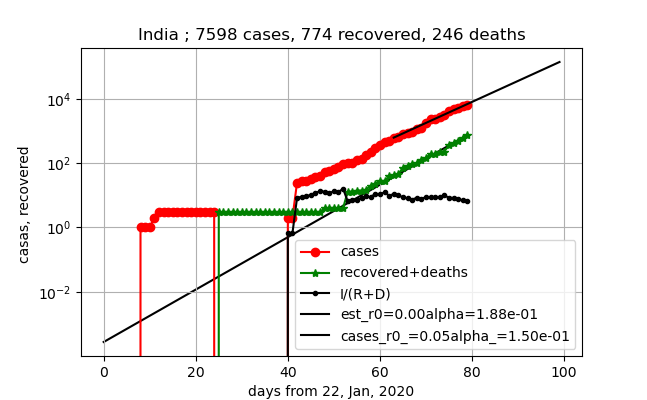
①上図赤プロット:まだまだこれから感染拡大しそう
②上図緑プロット;直線的に増加している
③上図黒プロットI/(R+D);10位の数字で一定値になっている
④下図青プロット;実効再生産数=10程度の大きな数値でほぼ一定
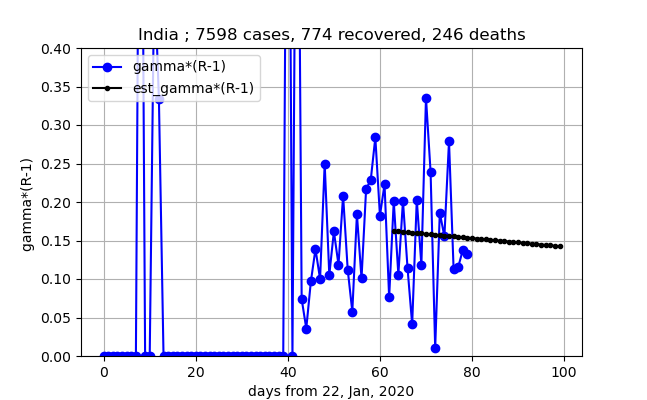
⑤誤差が大きいがほぼ一定のようだ
⑥単純に直線近似で引いているが、測定値は少しだけたれ始めた可能性もあるが、全体にまだまだ感染拡大しそうな勢いだ
まとめ
・日本、世界そして各国の状況を同じデータ処理をして並べてみた
・日本は実効再生産数が15と最大であり非常に危険な状況である。
人と人との接触率をできるだけ(80%以上)削減して感染拡大を抑え込みたい
・世界は少し感染数ピークが見え始めた段階
・ヨーロッパは感染数ピークが見え始め、これから終息が期待できそうであるが、予断を許さない状況
・韓国などは感染数ピーク後の終息に時間がかかっている
・武漢などは一度は終息が見えたが、まだまだ終息には時間がかかる状況
・北京と香港は第二波がそろそろ感染数ピークでこれから終息に向かう状況
・インドが感染拡大しつつあり、人口が多いのでこれから大変になる可能性がある
・記事にはたぶんしないが、これからも毎日動向をウオッチしたいと思う
おまけ;西浦さんの話;そういう生活スタイルの進め
西浦さんのご説明でわかりましたが、つまり大切なことは以下の二点である。
①第三方程式から、医療体制を充実して、$\gamma $を大きくし治癒速度(隔離率)を上げる
②第二方程式から、感染者との接触を極力小さくすると、$R-1$を小さくし、$R$を1以下にできれば感染を止められる
ということで、西浦さんのお話を以下ウワンなりの解説をします。
上記のSIRモデルにおいて、第二方程式から現存感染者数は指数関数的(ネズミ算的)な解をもつ。
ネズミ算は子供の数が小さいほどゆっくり増加する。
子供の数に相当するのが、この係数である$\gamma (R-1)$であり、これを小さく、特に0以下にすれば指数関数的に減少に転じる。つまり$R<1$を実現すればよい。
ちなみに、今ドイツでは$R_0 \fallingdotseq 2.5$であり、$R = R_0(1-p)$と書き換えると、
R_0(1-p) < 1
とできれば、$R-1<0$を実現できる。
上記の$R_0$を代入すると、
p=1-1/R_0=0.6
計算上は上記なのだけど、一部にこの計算以上の感染があるので、80%程度の削減が必要ということです。
もう少しきちんとしたご説明が以下にあります。
【参考】
・「このままでは8割減できない」 「8割おじさん」こと西浦博教授が、コロナ拡大阻止でこの数字にこだわる理由
しかし、上記のとおりドイツは世界でも優秀な国の一つで、日本だと現在$R \fallingdotseq 15$程度に増えています。これを$R_0 = 15$とすると、93%以上の削減が必要ということになります。
これは、式から分かるように感染に直接かかわる感染数に関連しています。
つまり、感染者が隔離されていれば、これは100%にできます。しかし、これは発症までに時間がかかる感染症では困難です(検査は一定の効果あるけど限界があります)。
また、今回は無症状感染者が感染させるという事象が報告されています。
ということで、感染者候補であるすべての人同士の接触0が目標になります。
接触0と言っても、感染には感染する条件を満たす接触半径のようなものがあります。
それが今回は2mと言われています。
以下のシミュレーションは感染半径を設定してその中に入った場合の感染確率を30%として、いろいろ計算しているのでイメージの参考にしてください。
・【シミュレーション入門】コロナ感染をシミュレートして遊んでみた♬
ということで上記の評価計算から、オンライン診察、オンライン治療、オンライン会議やオンライン飲み会、バーチャル〇〇、そして人と会う必要があるときも、十分な接触空間(少なくとも2m以上の間隔)や換気(マイクロ飛沫やエアロゾルの密度減少)、マスクの利用(自分の飛沫の拡散防止と他人の飛沫の一時防御)、そして時間差での感染を防ぐための手洗い、顔洗いを心がければ、100%感染者との接触を断つことが可能だと思います。
・出かけない
・集まらない
・マスク
・手洗い
の慣行がこれからの生活で一番大切な行為のひとつだと言えます。