最近のデータを自然に外挿したら以下のような図となった。
グラフ読める人は分かると思うが、かなりやばい状況だと認識した。
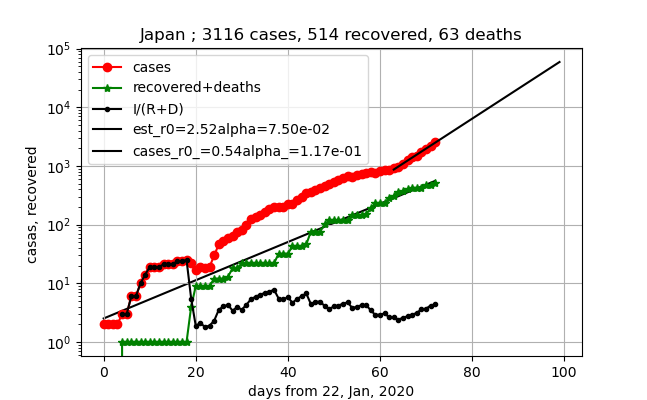
ということで、この話題には触れずに以下の話をしたいと思います。
今回扱うデータは参考サイト掲載の3/4/2020までのデータである。
なお、Japanの感染数は参考②より読み取った値を利用した。
【参考】
①Novel Coronavirus (COVID-19) Cases, provided by JHU CSSE
②データとグラフで見る新型コロナウイルス@日テレNEWS
やったこと
・SIRモデルの係数式変形
・SIRモデルの意味
・結果説明
・コード解説
・SIRモデルの係数式変形
今回は以下のSIRモデルを以下のように式変形することにより、$\gamma$そして実効再生産数の日々変化を求めようと思う。
{\begin{align}
\frac{dS}{dt} &= -\beta \frac{SI}{N} \\
\frac{dI}{dt} &= \beta \frac{SI}{N} -\gamma I \\
\frac{dr}{dt} &= \gamma I \\
\end{align}
}
まず、第三方程式から以下のように変形でき、これを使うと$I$と$r$は観測値が与えられているので、$\gamma$が求められる。
{\begin{align}
\frac{1}{I}\frac{dr}{dt} &= \gamma \\
\end{align}
}
次に、この$\gamma$を第二方程式に代入すると
{\begin{align}
\frac{1}{\gamma I}\frac{dI}{dt} &= R-1\\
R &= \frac{\beta}{\gamma} \frac{S}{N}\\
\end{align}
}
により、Rが求められる。
・SIRモデルの意味
この二つの量を用いると上記の微分方程式は以下のとおり、書き換えられる。
{\begin{align}
\frac{dS}{dt} &= -\gamma R I \\
\frac{dI}{dt} &= \gamma (R - 1) I \\
\frac{dr}{dt} &= \gamma I \\
\end{align}
}
ここで、$\gamma$は(回復率、隔離率、そして死亡率)に関係する因子であり、感染者が感染に寄与しなくなる(removedされる)割合を意味する。
一方、$R$は実効再生産数と呼ばれ、一人の感染者が感染させる人数に関係する量である。
したがって、第一式は$R$と$\gamma$が大きければ大きいほど、感染者に比例して感染が進むことを示す。これが感染拡大がいわゆるネズミ算で(指数関数的に)増える理由である。
一方、第三式は$\gamma$が大きいほど感染者に比例して治癒することを意味する。
そして、第二式は$(R-1)$に比例しており、この値の正負により、感染者が増大するか減少するかが決まることを示す。しかもその感染者数に比例するので指数関数的変化であることがわかる。そして、この変化も$\gamma$に比例する。
・結果説明
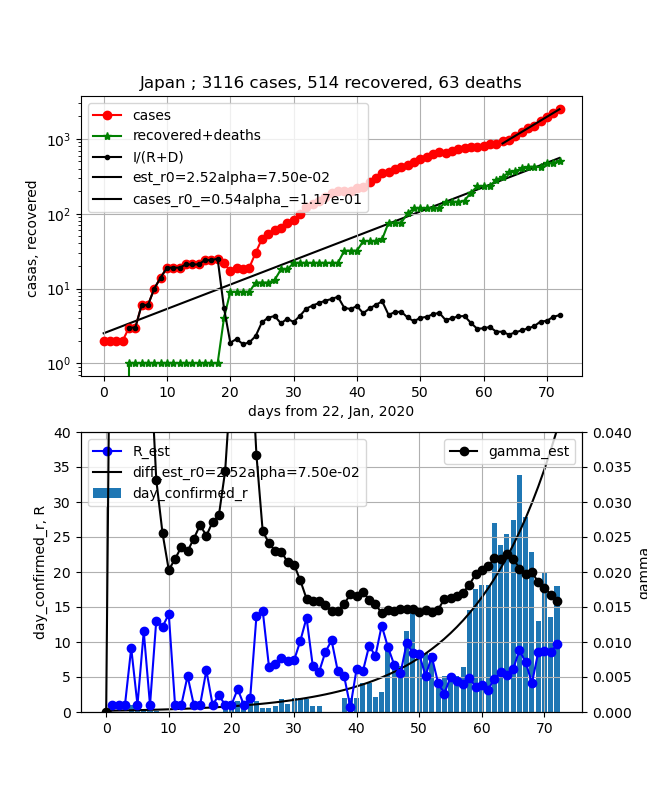
今回一番目を引くのは、やはり感染数(赤)が64日目(4月3日から9日前)から大きく変わってきたことである。
そして、今回の主眼はこの日本での流行に対して$\gamma$と$R$を求めることである。しかし上記のことそして何より日々のデータは揺らぎが大きいのでそれをどのようにするかが問題となった。
揺らぎはデータ見ると治癒数の曲線が酷いのが分かる。これをいわゆるスムージング(3点、5点、7点...)ということも考えたがそれ以上に酷いこと、そして全体としては、ほぼリニアに変化しているので、指数関数でフィッティングしてしまうこととした。
同じように、感染数もフィッティングしたが、これは直線部分のみ実施してみた。そして今回は最初に提示した外挿に利用したのみでこの係数計算では利用していない。
$I/(R+D)$の曲線は、感染者と感染に寄与しない人たちの比をプロットしたものである。
この数字は治癒率が上がり、この数字が減少し1を切るといよいよ終息が見えてくる数字である。
日本では一度3以下の数字になって、そのまま1に進んでいくと期待できたが、上記の64日目以降大きくこの数字も上昇に転じてしまった。しかもそれまでは弱弱しく減少していたのが、直線的に上昇始めたのでほんとに驚きである。
下段のグラフは今回求めたかった$\gamma$と$R$、そしてその計算で使う日々の治癒数(5日平均)とその近似曲線を示している。
$\gamma$は日々の治癒数(治癒曲線の微分)を感染数で除する。しかし治癒数曲線は揺らぎが大きいのでここで先ほど近似曲線を利用した。これでも感染数曲線の揺らぎのためにかなり揺らぎがでた。しかし、一応日々変化が見えて、この数字も64日目までは順調に治癒率が上昇したが、そこから直線的に下がってきてしまった。
一方、$R$は、この$\gamma$に反比例しており、結果もそのように動いている。ただし、最低値は実効再生産数3程度であり、その位置は少し左にずれている。いずれにしてもこのところは完全に増加してしまっており、実効再生産数が10辺りまで増加しつつあることが分かる。
直近の値は以下のとおりである。実効再生産数は1との比較であり、とても大きな値(急激に感染拡大していまう値)である。
{\begin{align}
\gamma &= 1.6e^{-2} \\
R &= 10 \\
\end{align}
}
実際の寄与は$\gamma (R-1)$に依存し、上記グラフは$\gamma$の減少の寄与と$R-1$の増大の寄与がバランスしていることが分かる。そこでこの量をグラフ化してみると以下のようなものになった。
この結果、$R$の寄与が大きく、一度0.05辺りまで減少したが、64日目を境に増加してしまっており、現在は0.14辺りまで増加したのが分かる。ここ二週間程度で感染確率が3倍程度になったと言える。
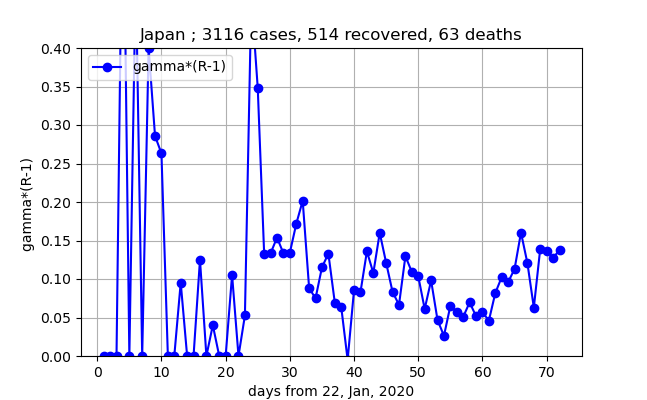
・コード解説
コード全体は以下に置いた
collective_particles/fitting_gamma_R.py
今回は主要な部分だけ解説する。
まず、データ読み込みと処理は以下のとおり。
city = "Japan"
skd=5 #2 #1 #4 #3 #2 #slopes average factor
# データを加工する
t_cases = 0
t_recover = 0
t_deaths = 0
for i in range(0, len(data_r), 1):
if (data_r.iloc[i][1] == city): #for country/region
#if (data_r.iloc[i][0] == city): #for province:/state
print(str(data_r.iloc[i][0]) + " of " + data_r.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed_r[day - 4] += data_r.iloc[i][day]
if day < 4+skd:
day_confirmed_r[day-4] += data_r.iloc[i][day]
else:
day_confirmed_r[day-4] += (data_r.iloc[i][day] - data_r.iloc[i][day-skd])/(skd)
t_recover += data_r.iloc[i][day]
for i in range(0, len(data_d), 1):
if (data_d.iloc[i][1] == city): #for country/region
#if (data_d.iloc[i][0] == city): #for province:/state
print(str(data_d.iloc[i][0]) + " of " + data_d.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed_d[day - 4] += data_d.iloc[i][day] #fro drawings
t_deaths += data_d.iloc[i][day]
for i in range(0, len(data), 1):
if (data.iloc[i][1] == city): #for country/region
#if (data.iloc[i][0] == city): #for province:/state
print(str(data.iloc[i][0]) + " of " + data.iloc[i][1])
for day in range(4, len(data.columns), 1):
confirmed[day - 4] += data.iloc[i][day] - confirmed_r[day - 4] -confirmed_d[day-4]
diff_confirmed[day - 4] += confirmed[day-4] / (confirmed_r[day - 4]+confirmed_d[day-4])
if day == 4:
day_confirmed[day-4] += data.iloc[i][day]
else:
day_confirmed[day-4] += data.iloc[i][day] - data.iloc[i][day-1]
治癒曲線のフィッティングは以下で実施。
t_max=len(confirmed)
dt=1
t=np.arange(0,t_max,dt)
t1=t
obs_i = confirmed_r[:]
# function which estimate i from seir model func
def estimate_i(ini_state,r0,alpha):
est = r0*np.exp(alpha*(t))
return est
def y(params):
est_i=estimate_i(ini_state,params[0],params[1])
return np.sum((est_i-obs_i)*(est_i-obs_i))
r0=1
alpha = 1
ini_state=[5.70579672, 0.00755685]
# optimize logscale likelihood function
mnmz=minimize(y,ini_state,method="nelder-mead")
print(mnmz)
r0,alpha = mnmz.x[0],mnmz.x[1]
est=estimate_i(ini_state,r0,alpha)
以下で諸量$\gamma$, $R$, $C=\gamma *(R-1)$を計算している。
diff_est=[0] * (len(data.columns) - 4)
gamma_est=[0] * (len(data.columns) - 4)
R_est = [0] * (len(data_d.columns) - 4)
R_0 = [0] * (len(data_d.columns) - 4)
C = [0] * (len(data_d.columns) - 4)
for i in range(1,t_max):
diff_est[i]=est[i]-est[i-1]
for i in range(0, len(confirmed), 1):
if confirmed[i] > 0:
gamma_est[i]=diff_est[i]/confirmed[i]
R_est[i]= 1+day_confirmed[i]/diff_est[i] # diff_est=gamma*confirmed
C[i]=gamma_est[i]*(R_est[i]-1)
else:
continue
あとは、以上の計算結果を描画している。
まとめ
・γとRをリアルなデータから求めた
・日本の状況はまさに危険地帯に突入したと言える
・βを求めていないのでやってみようと思う
・微分方程式で求めたものも含め、求めた各種パラメータの各国比較を実施しようと思う