Go to Qiita Advent Calendar Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Mrs_P

2つのグループの割合に差はあるか、母比率の差の信頼区間_統計検定2級対策

Posted at

以下の統計検定2級対策動画で用いられているスライドの一部です。

こんな「比較」に悩みませんか？

  • ECサイトのデザインAとB、どちらが購入率は高い？
  • 新薬を投与したグループと、そうでないグループで回復率に違いは？
  • 2つの製造ラインで作られた製品の不良品率に差はある？

本日のテーマ

この記事では、このような2つのグループの 比率（割合） の差を統計的に評価するための手法を解説します。


母比率の差の信頼区間

1. 具体例：ECサイトのA/Bテスト

あるECサイトで、新しい購入ボタンのデザイン（B案）が、従来のボタン（A案）よりも購入率を向上させるか検証するためにA/Bテストを実施しました。

  • 目的: 2つのデザインの購入率に差があるかを評価したい。
  • 手法: 95%信頼区間を求めて評価する。

A/Bテストの結果

A案 (従来デザイン) B案 (新デザイン)
表示ユーザー数 1200人 1100人
購入者数 150人 110人

このデータから、2つのデザインの購入率に統計的に意味のある差があるかを見ていきましょう。

Step 1: 各グループの購入率を計算する

まず、各デザインの購入率を計算します。
これは統計学で標本比率と呼ばれるものです。

  • A案の標本比率 $p_A$
    $$
    p_A = \frac{150}{1200} = 0.125 \quad (12.5%)
    $$

  • B案の標本比率 $p_B$
    $$
    p_B = \frac{110}{1100} = 0.100 \quad (10.0%)
    $$

Step 2: 購入率の差を計算する

次に、観測された2つの購入率の差を計算します。

$$
p_A - p_B = 0.125 - 0.100 = 0.025
$$

A案の購入率がB案より2.5%高いという結果が得られました。

しかし、この「2.5%の差」は、本当に意味のある差なのでしょうか？

それとも、単なる偶然による差なのでしょうか？

Step 3: 推定の「ばらつき」を評価する

計算した「2.5%の差」は、あくまで今回観測したサンプルでの結果です。サンプルが変われば、この差も変動します。

この推定値のばらつきの大きさを標準誤差と呼び、以下の式で計算します。

$$
SE = \sqrt{\frac{p_A(1-p_A)}{n_A} + \frac{p_B(1-p_B)}{n_B}}
$$

Step 3: 標準誤差の計算（実践）

実際に値を代入して計算してみましょう。

$$
\begin{aligned}
SE &= \sqrt{\frac{0.125(1-0.125)}{1200} + \frac{0.100(1-0.100)}{1100}} \
&\approx \sqrt{0.00009114 + 0.00008181} \
&\approx \sqrt{0.00017296} \
&\approx 0.01315
\end{aligned}
$$

推定値のばらつきの大きさ（標準誤差）は約0.01315と計算できました。

Step 4: 95%信頼区間を計算する

信頼区間 とは、「本当に知りたい真の差」が含まれていると推定される範囲のことです。

95%信頼区間 は、以下の式で計算します。

$$
(p_A - p_B) \pm 1.96 \times SE
$$

Step 4: 95%信頼区間の計算（実践）

これまでの計算結果を代入します。

$$
0.025 \pm 1.96 \times 0.01315
$$

$$
0.025 \pm 0.025774
$$

  • 下限値: $0.025 - 0.025774 = -0.000774$
  • 上限値: $0.025 + 0.025774 = 0.050774$

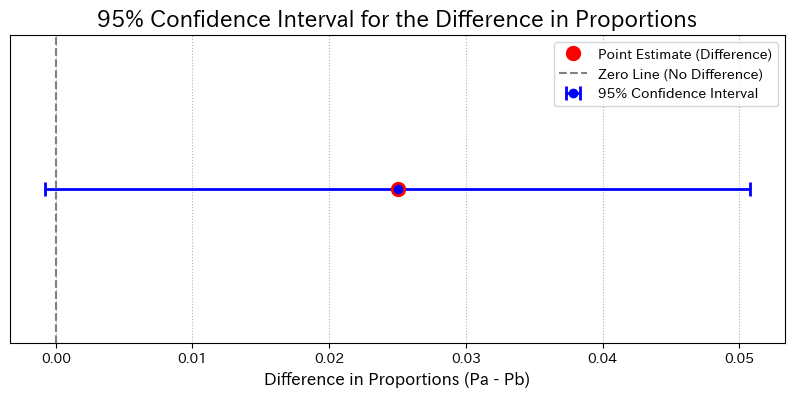
A/Bテストの結論

算出された95%信頼区間は以下の通りです。


[-0.0008, 0.0508]

では、この結果をどのように解釈すればよいのでしょうか？

2. 結果の解釈

結果を解釈する上で、最も重要なポイントがあります。


信頼区間が 0 を含むか？


今回の区間 [-0.0008, 0.0508] は、マイナスの値からプラスの値にまたがっているため、0 を含んでいます。

image.png

信頼区間と「0」の関係（今回の結果）

image.png

import matplotlib.pyplot as plt
import numpy as np

# Data
point_estimate = 0.025
lower_bound = -0.000774
upper_bound = 0.050774
error = upper_bound - point_estimate

# Plot
fig, ax = plt.subplots(figsize=(10, 4))

# Error bar
ax.errorbar(point_estimate, 0, xerr=error, fmt='o', color='blue',
            capsize=5, capthick=2, elinewidth=2, label='95% Confidence Interval')

# Point estimate
ax.plot(point_estimate, 0, 'o', color='red', markersize=10, label='Point Estimate (Difference)')

# Zero line
ax.axvline(0, color='gray', linestyle='--', label='Zero Line (No Difference)')

# Title and labels
ax.set_title('95% Confidence Interval for the Difference in Proportions', fontsize=16)
ax.set_xlabel('Difference in Proportions (Pa - Pb)', fontsize=12)

# Y-axis settings
ax.set_yticks([])
ax.set_ylim(-0.5, 0.5)

ax.legend()
ax.grid(axis='x', linestyle=':')
plt.show()

解釈①: 信頼区間が「0」を含む場合（今回）

  • 結果: 信頼区間が 0 を含んでいる。
  • 意味: 2つの購入率の差が 0 である可能性を否定できない。
  • 結論:

95%の信頼水準において、2つのデザインの購入率に統計的に有意な差があるとは言えない。

(参考) 解釈②: もし信頼区間が「0」を含まなかったら？

  • 例1: 区間が [0.01, 0.05] (すべて正)

    • 差は正であると推定されます。
    • 結論: A案の方がB案より購入率が高いと言える。

  • 例2: 区間が [-0.06, -0.02] (すべて負)

    • 差は負であると推定されます。
    • 結論: B案の方がA案より購入率が高いと言える。

3. 一般化と定義

ここまでの具体例を、一般的な言葉と数式で整理します。

母比率の差とは

2つの異なる母集団における、特定の性質を持つ要素の割合（母比率）の差のことです。

  • 母集団1の母比率: $P_1$
  • 母集団2の母比率: $P_2$

私たちが本当に知りたいのは、この $P_1 - P_2$ です。
しかし、母集団全体を調査することは困難なため、標本データからこの値を推定します。

計算のための記号整理

グループ1 グループ2
標本の大きさ $n_1$ $n_2$
特定の性質を持つ要素の数 $x_1$ $x_2$
標本比率 $p_1 = \frac{x_1}{n_1}$ $p_2 = \frac{x_2}{n_2}$

母比率の差の信頼区間 (一般式)

標本の大きさが十分大きい場合、母比率の差の信頼区間は以下の式で計算します。

$$
(p_1 - p_2) \pm z_{\alpha/2} \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}
$$

  • $(p_1 - p_2)$ は標本比率の差
  • $z_{\alpha/2}$ は信頼度によって決まる値（例: 95%信頼区間なら $z_{0.025} \approx 1.96$ ）
  • $\sqrt{...}$ の部分は標準誤差

まとめ

  • 母比率の差の信頼区間 は、2つのグループの比率に意味のある差があるかを評価する強力な手法です。

  • 標本データから標本比率の差と標準誤差を計算し、信頼区間を求めます。

  • 結果の解釈では、算出した信頼区間が 0 を含むかどうかが鍵となります。

    • 含む: 有意な差があるとは言えない
    • 含まない: 有意な差があると言える

参考：数式による理論的背景

理論の出発点：二項分布

A/Bテストのように、「購入か非購入か」といった2択の結果を扱う場合、確率変数である 購入者数 （例：1200人のうち何人が購入したか）が従う確率分布は、本来は 二項分布 と呼ばれるものです。

  • しかし、二項分布はそのまま扱うと計算が複雑になりがちです。

  • 幸いなことに、サンプルサイズ（例：訪問者数）が十分に大きい場合、二項分布は 正規分布 で非常によく近似できることが知られています。

ここからの解説は、この「正規分布による近似」を前提としています。

理論の前提：正規分布への近似

上記の背景から、母比率の差の検定や推定は、主に以下の2つの統計的な性質に基づいています。

  • 標本比率の正規近似

    • サンプルサイズ $n$ が十分に大きい場合、標本比率 $\hat{p}$ の分布は、平均 $p$ 、分散 $\frac{p(1-p)}{n}$ の正規分布で近似できます。

  • 正規分布の再生性

    • 互いに独立な正規分布に従う確率変数の和や差も、また正規分布に従います。

標本比率の差が従う分布

上記の性質から、2つの独立した標本比率の差 $\hat{p}_1 - \hat{p}_2$ もまた、近似的に正規分布に従います。

  • 平均: $p_1 - p_2$
  • 分散: $\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}$

数式で表すと以下のようになります。

$$
\hat{p}_1 - \hat{p}_2 \sim N \left( p_1 - p_2, \frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2} \right)
$$

標本比率の差の標準化

正規分布に従う確率変数は、 標準化 を行うことで、平均が0、分散が1の 標準正規分布 $N(0, 1)$ に従います。

標準化 = (確率変数 - 平均) / 標準偏差

標本比率の差を標準化すると、以下の式が得られます。

$$
\frac{(\hat{p}_1 - \hat{p}_2) - (p_1 - p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} \sim N(0, 1)
$$

検定統計量 Z への応用

この標準化された値が、仮説検定で用いられる 検定統計量 $Z$ です。

$$
Z = \frac{(\hat{p}_1 - \hat{p}_2) - (p_1 - p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}}
$$

信頼区間の計算やZ検定では、この $Z$ が標準正規分布に従うことを利用して、「観測された差が統計的に意味のあるものか」を評価します。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?