Go to Qiita Advent Calendar Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Mrs_P

自己相関とコレログラム_統計検定2級対策

Posted at

以下の統計検定2級対策動画で用いられているスライドの一部です。

ステップ1：具体例から学ぼう

難しい定義から入るのではなく、まずは 具体的なデータ を使って 自己相関 の考え方を掴んでいきましょう。

今回使用するデータ
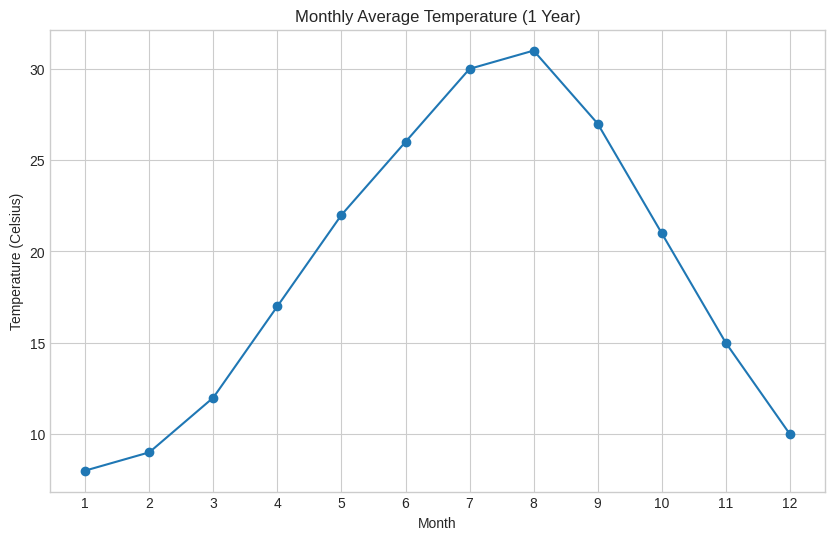
ある都市における1年間の月間平均気温データ（架空）

月 1 2 3 4 5 6 7 8 9 10 11 12
気温(℃) 8 9 12 17 22 26 30 31 27 21 15 10

まずはデータを可視化してみよう

この気温データを折れ線グラフにすると、時間的なパターンがはっきりと見えてきます。

image.png

import matplotlib.pyplot as plt
import pandas as pd

# Data
data = {
    'Month': range(1, 13),
    'Temperature': [8, 9, 12, 17, 22, 26, 30, 31, 27, 21, 15, 10]
}
df = pd.DataFrame(data)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(df['Month'], df['Temperature'], marker='o', linestyle='-')
plt.title('Monthly Average Temperature (1 Year)')
plt.xlabel('Month')
plt.ylabel('Temperature (Celsius)')
plt.grid(True)
plt.xticks(range(1, 13))
plt.show()

グラフから生まれる疑問

グラフを見ると、ある月の気温とその前後の月の気温には、何らかの関係がありそうです。

「今月の気温は、先月の気温とどれくらい関係があるのか？」

  • このような、時系列データにおける 時間的なつながり こそが 自己相関 です。
  • そして、比較する時間のズレ（例：1ヶ月）のことを ラグ と呼びます。

関係性を数値で評価する

「関係がありそう」という感覚を、客観的な数値で評価してみましょう。

そのために使う指標が 自己相関係数 (Autocorrelation Function, ACF) です。

これから、実際に ラグ1 (1ヶ月ズレ) の自己相関係数を計算していきます。

計算プロセス ①：平均値の計算

まず、計算の基準となるデータの平均値を求めます。

  • Step 1: 平均値 $\bar{y}$ の計算
    $$
    \bar{y} = \frac{8+9+12+17+22+26+30+31+27+21+15+10}{12} = \frac{228}{12} = 19
    $$

データの平均気温は 19℃ です。

計算プロセス ②：分散の計算

次に、データのばらつき具合を示す 分散 を計算します。
これは、時間のズレがない ラグ0の自己共分散 $C_0$ と同じ意味です。

  • Step 2: 分散 $C_0$ の計算
    $$
    C_0 = \frac{1}{12} \sum_{t=1}^{12} (y_t - 19)^2
    $$
    $$
    C_0 = \frac{(8-19)^2 + (9-19)^2 + \dots + (10-19)^2}{12} = \frac{762}{12} = 63.5
    $$

データの分散は 63.5 です。

計算プロセス ③：自己共分散の計算

いよいよ、1ヶ月ずらしたデータ同士の関係性 (ラグ1の自己共分散) を計算します。

  • Step 3: ラグ1の自己共分散 $C_1$ の計算
    $$
    C_1 = \frac{1}{12} \sum_{t=1}^{11} (y_t - 19)(y_{t+1} - 19)
    $$
    $$
    C_1 = \frac{(-11)(-10) + (-10)(-7) + \dots + (-4)(-9)}{12} = \frac{558}{12} = 46.5
    $$

ラグ1の自己共分散は 46.5 です。

計算プロセス ④：自己相関係数の計算

最後に、自己共分散を分散で割ることで、関係性の強さを $-1$ から $1$ の範囲に標準化します。

  • Step 4: ラグ1の自己相関係数 $r_1$ の計算
    $$
    r_1 = \frac{C_1}{C_0} = \frac{46.5}{63.5} \approx 0.732
    $$

ラグ1の自己相関係数は 約0.732 となりました。

計算結果の解釈

自己相関係数は、-1から1までの値をとり、その意味は以下の通りです。

  • 1 に近い: 強い 正の相関 がある
    (過去が高いと現在も高い傾向)
  • -1 に近い: 強い 負の相関 がある
    (過去が高いと現在は低い傾向)
  • 0 に近い: ほとんど相関がない

今回の結果 0.732 は、「ある月の気温は、その前の月の気温と強い正の相関を持つ」 ことを示しています。

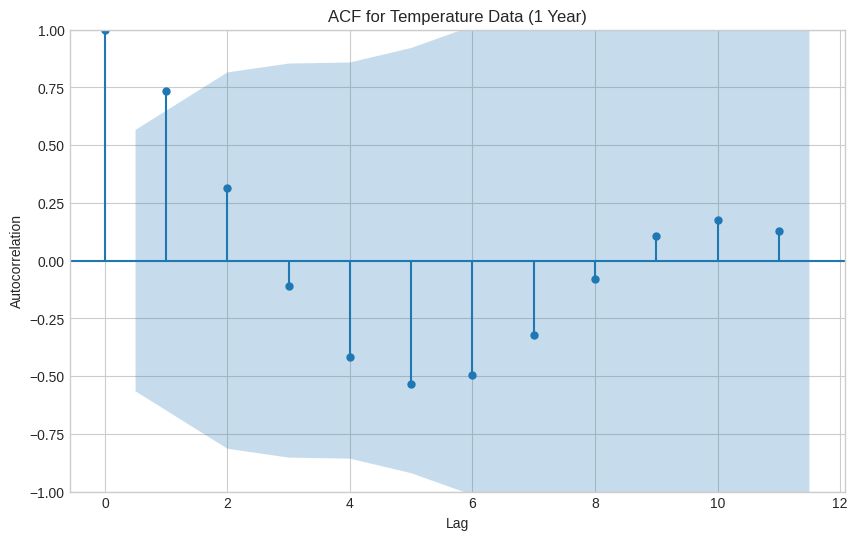
自己相関の可視化：コレログラム（1年分）

ラグを1, 2, 3, ...と増やしながら各ラグの自己相関係数を計算し、グラフにしたものが コレログラム です。

image.png

import matplotlib.pyplot as plt
import pandas as pd
from statsmodels.graphics.tsaplots import plot_acf

# Data (1 year)
temperature = [8, 9, 12, 17, 22, 26, 30, 31, 27, 21, 15, 10]
series = pd.Series(temperature)

# Plotting ACF
fig, ax = plt.subplots(figsize=(10, 6))
plot_acf(series, ax=ax, lags=11)
ax.set_title('ACF for Temperature Data (1 Year)')
ax.set_xlabel('Lag')
ax.set_ylabel('Autocorrelation')
plt.grid(True)
plt.show()

コレログラムの読み方

コレログラムは、データの時間的な特徴を直感的に理解するのに役立ちます。

  • 棒グラフ: 各ラグにおける自己相関係数の値を示します。
  • 青い帯 (信頼区間): 棒がこの範囲内に収まっている場合、その相関は「統計的に意味がない（偶然の可能性がある）」と解釈します。

信頼区間を大きく超える棒 に注目することが重要です！

image.png

1年分データでのコレログラム解釈

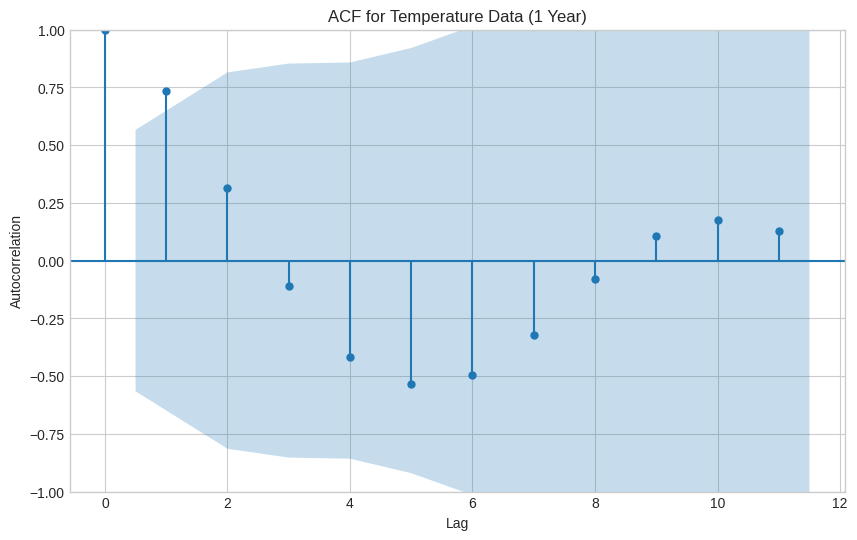
実際に作成されたコレログラムを見てみましょう。

  • ラグ1, 2

    • 信頼区間を大きく超えており、強い正の相関 があることが分かります。
    • これは「ある月の気温は、直前の月の気温に強く影響される」という 持続性 を示しています。

  • ラグ6付近

    • 予測通り相関は負になっていますが、信頼区間の範囲内です。

考察
1年分のデータからは 強い持続性 が証明できました。
しかし、季節性のパターンは見え隠れしているものの、データ数が少ないため、統計的に有意であるとまでは言えませんでした。

ステップ2：発展 - データ数を増やしてみる

では、もしデータがもっと長期間、例えば 5年分 あったらコレログラムはどう変化するでしょうか？

仮説
データ数が増えれば、偶然の可能性が減るため信頼区間は狭くなるはず。
その結果、これまで隠れていた 季節性 が明確に見えてくるのではないか？

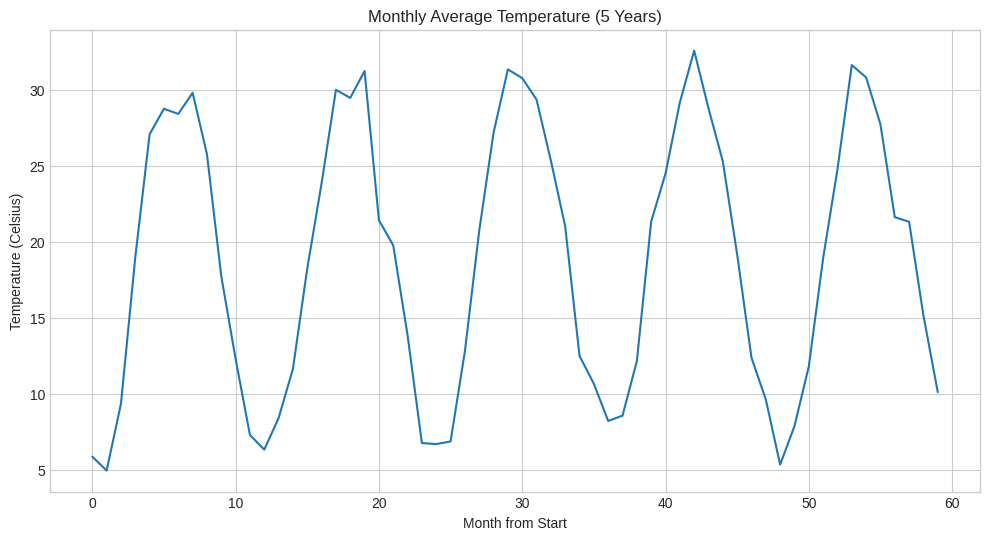
5年分のデータで可視化

5年分（60ヶ月）の架空の気温データを用意し、グラフにしてみます。
年ごとの多少の変動はありますが、明確な季節周期が見て取れます。

image.png

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# --- 5年分の架空データを生成 ---
# 期間設定
n_years = 5
n_months = n_years * 12

# 時間軸 (0から59までの60ヶ月)
time = np.arange(n_months)

# 1. 季節周期の成分を作成 (cos波を利用)
# 12ヶ月周期で、夏に高く冬に低くなるパターン
amplitude = 12  # 振幅（季節による気温差）
baseline_temp = 19 # 年間平均気温
seasonal_component = -amplitude * np.cos(2 * np.pi * time / 12)

# 2. 不規則な変動（ノイズ）成分を作成
# 現実のデータに近づけるためのランダムなばらつき
noise = np.random.normal(0, 1.5, n_months) # 平均0, 標準偏差1.5の正規分布ノイズ

# 3. 成分を合成して最終的な気温データを生成
temperature_5years = baseline_temp + seasonal_component + noise

# Pandas DataFrameに格納
df_5years = pd.DataFrame({
    'Time': time,
    'Temperature': temperature_5years
})
# ------------------------------

# Plotting
plt.figure(figsize=(12, 6))
plt.plot(df_5years['Time'], df_5years['Temperature'])
plt.title('Monthly Average Temperature (5 Years)')
plt.xlabel('Month from Start')
plt.ylabel('Temperature (Celsius)')
plt.grid(True)
plt.show()

コレログラムの変化（5年分）

5年分のデータでコレログラムを作成すると、変化が現れます。

image.png

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf

# --- 5年分の架空データを生成 (グラフの時と同じデータ) ---
# 期間設定
n_years = 5
n_months = n_years * 12

# 時間軸 (0から59までの60ヶ月)
time = np.arange(n_months)

# 1. 季節周期の成分を作成 (cos波を利用)
amplitude = 12
baseline_temp = 19
seasonal_component = -amplitude * np.cos(2 * np.pi * time / 12)

# 2. 不規則な変動（ノイズ）成分を作成
noise = np.random.normal(0, 1.5, n_months)

# 3. 成分を合成して最終的な気温データを生成
temperature_5years = baseline_temp + seasonal_component + noise

# Pandas Seriesに変換
series_5years = pd.Series(temperature_5years)
# ------------------------------


# Plotting ACF for 5 years
fig, ax = plt.subplots(figsize=(10, 6))
plot_acf(series_5years, ax=ax, lags=24) # 24ヶ月分表示
ax.set_title('ACF for Temperature Data (5 Years)')
ax.set_xlabel('Lag')
ax.set_ylabel('Autocorrelation')
plt.grid(True)
plt.show()

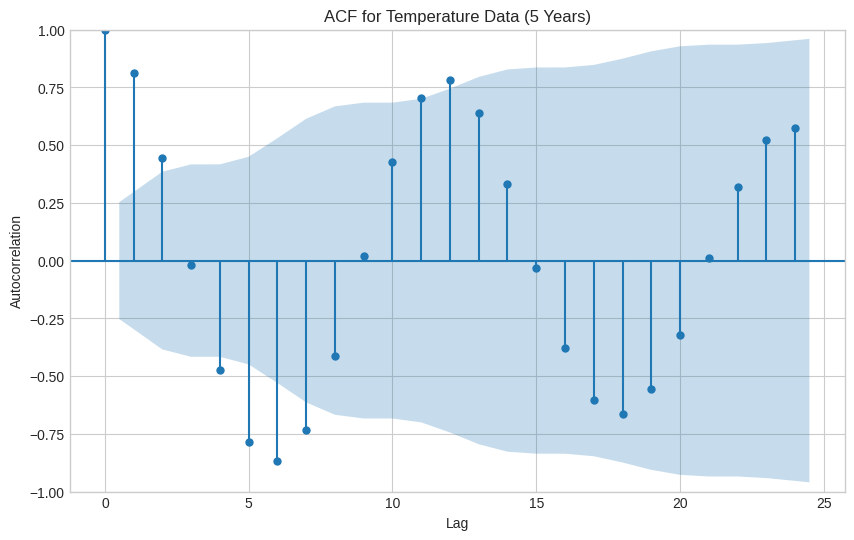
5年分データでのコレログラム解釈

データ数を増やした結果、コレログラムから多くのことが読み取れるようになりました。

✅ 信頼区間が非常に狭くなった！

  • データ数が増えたことで統計的な確信度が高まり、わずかな相関でも「意味がある」と判断しやすくなりました。

✅ 季節性が明確になった！

  • ラグ6: 強い 負の相関（夏と冬）。
  • ラグ12: 強い 正の相関（1年前の同じ季節）。
  • ラグ18, 24...: 周期的な相関が続いている。

結論
データ数を増やすことで、持続性 に加えてデータの持つ 周期性・季節性 を統計的に証明することができました。

補足：「ラグが大きい＝無意味」ではない！

コレログラムを見ると、ラグが大きくなるにつれて信頼区間（青い帯）が少しずつ広がっていることに気づきます。

よくある誤解
「ラグが大きい相関は、信頼区間に入りやすいし、重要ではないのでは？」
→ 答えは「No」です！ 特に周期性のあるデータでは逆です。

✅ ポイント１：季節性の発見

  • 気温データのように周期性を持つ場合、特定の大きなラグにこそ重要な意味が隠されています。
  • ラグ12, 24: 1年前、2年前の同じ季節との関係（強い正の相関）を示しており、データの季節性を捉える鍵となります。

✅ ポイント２：信頼区間の正しい理解

  • ラグが大きくなると信頼区間が広がるのは、「相関が弱くなった」からではなく、「比較できるデータ数が減り、統計的な確信度が下がった」からです。
  • その広い信頼区間をさらに超えてくる大きなラグの相関は、偶然とは考えにくく、むしろ 「非常に強い関係性がある」 ことを示唆しています。

ステップ3：一般化と定義

ここまでの具体例を踏まえて、用語と計算式を一般化して整理しましょう。

定義：自己相関 (Autocorrelation)

一つの時系列データにおいて、ある時点の値と、それより過去の時点の値との間に存在する 線形な関係性 のこと。

  • 時点 $t$ の値 $y_t$ と、そこから ラグ $k$ だけ離れた過去の時点 $t-k$ の値 $y_{t-k}$ との間の相関を指します。
  • データの 周期性 や 持続性 といった、時間的な依存構造を定量的に把握するために用います。

定義：自己相関係数 (ACF) と計算式

自己相関の強さを $-1$ から $1$ の数値で定量化する指標です。

  1. 平均値 $\bar{y}$
    $$ \bar{y} = \frac{1}{n} \sum_{t=1}^{n} y_t $$

  2. ラグ $k$ の自己共分散 $C_k$
    $$ C_k = \frac{1}{n} \sum_{t=1}^{n-k} (y_t - \bar{y})(y_{t+k} - \bar{y}) $$

  3. ラグ $k$ の自己相関係数 $r_k$
    $$ r_k = \frac{C_k}{C_0} \quad \left( \text{ただし} ; C_0 = \frac{1}{n} \sum_{t=1}^{n} (y_t - \bar{y})^2 \right) $$

まとめ

本日の学習内容を振り返りましょう。

  • 自己相関
    • 時系列データ内の時間的に離れた点同士の関係性。
  • 自己相関係数 (ACF)
    • 関係性の強さを $-1$ から $1$ の数値で定量化する指標。
  • コレログラム
    • ACFを可視化し、データの周期性や持続性を直感的に理解するためのグラフ。
  • データ数の重要性
    • データ数が多いほど、より信頼性の高い分析が可能になる。

自己相関の理解は、ARモデルなど、より高度な時系列分析への第一歩です。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?