以下の統計検定2級対策動画で用いられているスライドの一部です。
今回のテーマ
- 母集団のデータの ばらつき を示す 母分散 ($\sigma^2$) を推定します。
- ある一点の値ではなく、確率的に信頼できる 区間 を求めます。
- この計算には、 カイ二乗分布 ($\chi^2$分布) という確率分布を利用します。
学習の流れ
まずは具体的な例題を通して、計算の流れを体験します。
その後に、背景にある理論や公式を整理し、理解を深めます。
-
Step 1: 具体的な計算例から学ぶ
- 問題設定から結論まで、一連のプロセスを追体験します。
-
Step 2: 一般化と定義のまとめ
- 計算例で使った考え方を、一般的な定義と公式に落とし込みます。
Step 1: 具体的な計算例 - 問題設定
ある工場で、部品の重量を管理しています。
その精度を評価するため、以下の調査を行いました。
-
調査内容
- 15個の部品を無作為に抽出
- 重量を測定し、 不偏分散 を計算
- 結果: $s^2 = 25.0$ (mg$^2$)
ただし、この部品の重量は正規分布に従うものとします。
この結果から、部品重量の母分散$\sigma^2$に対する 90%信頼区間 を求めてみましょう。
解答プロセス (1) 条件の確認
問題文から、計算に必要な情報を整理します。
- 標本サイズ: $n = 15$
- 不偏分散: $s^2 = 25.0$
- 信頼係数: $1-\alpha = 0.90$
- 有意水準: $\alpha = 1 - 0.90 = 0.10$
- 信頼区間の外側に出る確率。両側に$\alpha/2 = 0.05$ずつ割り振ります。
解答プロセス (2) なぜカイ二乗分布?
母分散の信頼区間を求めるには、カイ二乗分布が持つ以下の重要な性質を利用します。
母集団が正規分布に従うとき、標本の大きさ$n$、不偏分散$s^2$から計算される統計量$\frac{(n-1)s^2}{\sigma^2}$は、ある特定の確率分布に従います。
$$
\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)
$$
この統計量は、 自由度$n-1$のカイ二乗分布 に従います。
解答プロセス (3) 自由度を求める
今回の問題に、この性質を当てはめます。
- 標本サイズ$n = 15$なので、自由度 (df) は、
$$
df = n - 1 = 15 - 1 = 14
$$ - したがって、 自由度14のカイ二乗分布 を使って計算を進めます。
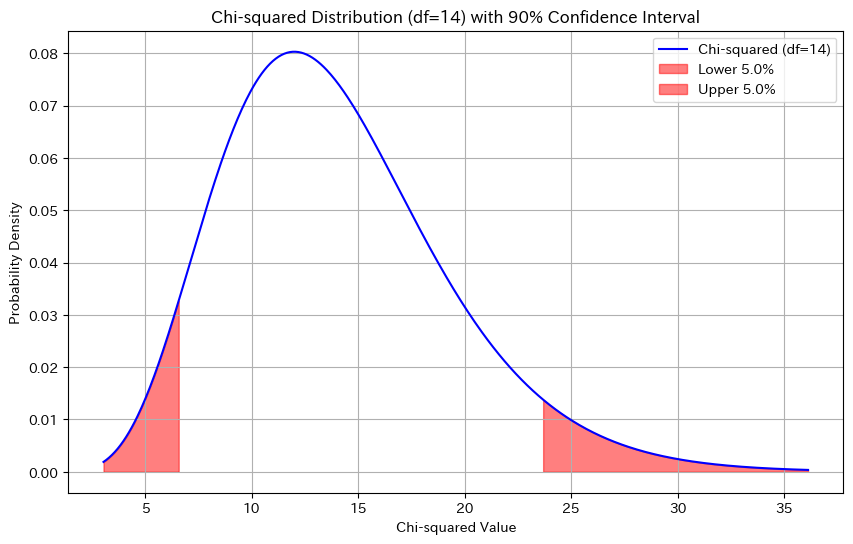
カイ二乗分布の可視化
自由度14のカイ二乗分布と、90%信頼区間(両側5%)の関係を視覚的に確認しましょう。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
# Parameters
df = 14
confidence_level = 0.90
alpha = 1 - confidence_level
# Critical values
chi2_lower = chi2.ppf(alpha / 2, df)
chi2_upper = chi2.ppf(1 - alpha / 2, df)
# X values for the plot
x = np.linspace(chi2.ppf(0.001, df), chi2.ppf(0.999, df), 500)
y = chi2.pdf(x, df)
# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'b-', label=f'Chi-squared (df={df})')
# Shade the area outside the confidence interval
x_fill_lower = np.linspace(chi2.ppf(0.001, df), chi2_lower, 100)
y_fill_lower = chi2.pdf(x_fill_lower, df)
plt.fill_between(x_fill_lower, y_fill_lower, color='red', alpha=0.5, label=f'Lower {alpha/2*100:.1f}%')
x_fill_upper = np.linspace(chi2_upper, chi2.ppf(0.999, df), 100)
y_fill_upper = chi2.pdf(x_fill_upper, df)
plt.fill_between(x_fill_upper, y_fill_upper, color='red', alpha=0.5, label=f'Upper {alpha/2*100:.1f}%')
# Add labels and title
plt.title(f'Chi-squared Distribution (df={df}) with {confidence_level*100:.0f}% Confidence Interval')
plt.xlabel('Chi-squared Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()
解答プロセス (4) カイ二乗分布の値を求める
カイ二乗分布表から、自由度14における両側の棄却域の境界値(パーセント点)を読み取ります。
-
上側5%点 ($\alpha/2 = 0.05$)
- $\chi^2_{0.05, 14} = 23.685$
-
下側5%点 (上側95%点, $1-\alpha/2 = 0.95$)
- $\chi^2_{0.95, 14} = 6.571$
これらの値が、信頼区間を計算するための重要な要素となります。
解答プロセス (5) 信頼区間の計算(下限)
信頼区間の 下限値 を計算します。
分母には、先ほど求めたカイ二乗値のうち 大きい方 ($\chi^2_{0.05, 14}$) を使います。
$$
\frac{(n-1)s^2}{\chi^2_{0.05, 14}} = \frac{(15-1) \times 25.0}{23.685}
$$
$$
= \frac{350}{23.685} \approx 14.775
$$
解答プロセス (6) 信頼区間の計算(上限)
次に、信頼区間の 上限値 を計算します。
分母には、カイ二乗値のうち 小さい方 ($\chi^2_{0.95, 14}$) を使います。
$$
\frac{(n-1)s^2}{\chi^2_{0.95, 14}} = \frac{(15-1) \times 25.0}{6.571}
$$
$$
= \frac{350}{6.571} \approx 53.264
$$
解答プロセス (7) 結論
計算結果をまとめます。
この工場で製造される部品の重量の母分散$\sigma^2$に対する 90%信頼区間 は、
[14.78, 53.26] (mg$^2$)
であると推定されます。
Step 2: 一般化と定義のまとめ
ここまでの具体例を踏まえ、母分散の信頼区間の考え方を一般化し、定義と公式を整理します。
母分散の信頼区間とは?
- 調査や実験で得られるデータは 標本 であり、そこから計算されるのは 不偏分散 ($s^2$) です。
- 私たちが本当に知りたいのは、母集団全体のばらつきである 母分散 ($\sigma^2$) です。
母分散の信頼区間 とは、標本データをもとに、「未知である真の母分散$\sigma^2$が、ある確率(信頼係数)で含まれると推定される区間」のことです。
信頼区間の導出プロセス (1)
信頼区間の公式は、カイ二乗分布の性質から導かれます。
まず、以下の確率的な関係式からスタートします。
$$
P \left( \chi^2_{1-\alpha/2, n-1} \le \frac{(n-1)s^2}{\sigma^2} \le \chi^2_{\alpha/2, n-1} \right) = 1-\alpha
$$
この式の意味は、「統計量$\frac{(n-1)s^2}{\sigma^2}$が、カイ二乗分布の下側と上側の点の間に収まる確率は$1-\alpha$である」ということです。
信頼区間の導出プロセス (2)
次に、この不等式を、求めたい$\sigma^2$について変形します。
-
各辺の逆数をとる
- 不等号の向きが逆転します。
$$
\frac{1}{\chi^2_{\alpha/2, n-1}} \le \frac{\sigma^2}{(n-1)s^2} \le \frac{1}{\chi^2_{1-\alpha/2, n-1}}
$$
- 不等号の向きが逆転します。
-
各辺に$(n-1)s^2$を掛ける
- 中央が$\sigma^2$だけになり、公式が導かれます。
母分散の信頼区間の公式
以上のプロセスから、信頼係数$1-\alpha$の母分散$\sigma^2$の信頼区間の公式が導かれます。
$$
\frac{(n-1)s^2}{\chi^2_{\alpha/2, n-1}} \le \sigma^2 \le \frac{(n-1)s^2}{\chi^2_{1-\alpha/2, n-1}}
$$
-
ポイント
- 区間の 下限 の分母は、カイ二乗分布の 上側 の点 ($\chi^2_{\alpha/2, n-1}$)
- 区間の 上限 の分母は、カイ二乗分布の 下側 の点 ($\chi^2_{1-\alpha/2, n-1}$)
まとめ
-
Point 1: カイ二乗分布の利用
- 統計量$\frac{(n-1)s^2}{\sigma^2}$が、自由度$n-1$のカイ二乗分布に従う性質がすべての基本です。
-
Point 2: 信頼区間の公式
$$
\frac{(n-1)s^2}{\chi^2_{\alpha/2, n-1}} \le \sigma^2 \le \frac{(n-1)s^2}{\chi^2_{1-\alpha/2, n-1}}
$$ -
Point 3: 計算上の注意点
- 分母に来るカイ二乗値が、区間の 下限と上限で入れ替わる ことを忘れないようにしましょう。