本記事では、PyTorch を用いた Stiefel 多様体上の最適化手法について紹介する。
ここで、Stiefel 多様体とは直交制約を満たす以下の行列の集合で表される。
\begin{equation}
\mathop{\mathrm{St}}(n,m)=\left\{X\in\mathbb R^{n\times m}\mid X^\top X=I_{m\times m}\right\}
\end{equation}
PyTorch を用いた Stiefel 多様体上の最適化、特に深層学習における Stiefel 多様体上の最適化においては、以下の2つの手法がよく用いられる。
- Regularizer-based method
正則化項 $\frac14|X^\top X - I_{m\times m}|_2^2$ を用いる手法 - Retraction-based method
リーマン多様体上の最適化手法を用いる手法
また、本記事では簡単な実装例を紹介するために以下の例題を SGD を用いて解くことを考える。
\begin{align}
\max_{X\in\mathop{\mathrm{St}}(n,m)}\frac12\|AX\|_F^2
\end{align}
ここで、$A\in\mathbb R^{N\times n}$ は $n$ 次元の特徴量を $N$ 個並べた行列であり、最適解は $A$ の上位 $m$ 個の特異値に対応する右特異ベクトルである。
(実装では目的関数をバッチサイズでスケーリングして扱う)
本記事では、乱数を用いて生成した以下のデータ行列を使用する。
import torch
n = 5000
m = 200
N = 15000
sigma = 0.1
U, _ = torch.linalg.qr(torch.randn(n, m))
multinormal = torch.distributions.MultivariateNormal(
torch.zeros(n),
U @ U.T + sigma * torch.eye(n),
)
A = multinormal.rsample([N])
最適値は以下で計算できる。
u, s, v = torch.linalg.svd(A, full_matrices=False)
x_optim = v[:m].T
dot = A @ x_optim
optimal = torch.sum(dot * dot, dim=1).mean()
Regularizer-based Method
深層学習において、畳み込みや全結合層の重みに直交制約を課すことで精度向上やロバスト性、過学習回避などが報告されている。
- Regularizing CNNs with Locally Constrained Decorrelations
- Parseval Networks: Improving Robustness to Adversarial Examples
- Can We Gain More from Orthogonality Regularizations in Training Deep CNNs?
- Orthogonal Convolutional Neural Networks
これらの手法の中には、直交制約を満たすために正則化項 $\frac14|X^\top X - I_{m\times m}|_2^2$ を用いるものがある。
PyTorch では以下のように実装できる。
まず、乱数固定と初期化の関数を実装する。
import random
import numpy as np
def set_random_seed(seed=None):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
def init_weight(n, p):
weight, _ = torch.linalg.qr(torch.randn(n, p))
return weight
重みの更新は、PyTorch のサンプル を参考に実装する。
import torch.nn.functional as F
from torch.utils.data import DataLoader
from tqdm.auto import trange
# initialize
set_random_seed(42)
weight = init_weight(n, m).requires_grad_(True)
# dataloader
batch_size = 128
dataloader = DataLoader(A, batch_size=batch_size, shuffle=True)
# optimizer
momentum = 0.
lr = 0.002
step_size = 30
gamma = 0.1
optimizer = torch.optim.SGD([weight], lr=lr, momentum=momentum)
scheduler = torch.optim.lr_scheduler.StepLR(
optimizer, step_size=step_size, gamma=gamma
)
# train loop
epochs = 60
lambd = 10
log = dict(time=[], epoch=[], lr=[], loss=[], reg_loss=[])
for i in trange(epochs):
for x in dataloader:
if x.shape[0] < batch_size:
continue
t1 = time.time()
# objective function
x = x @ weight
norm = torch.sum(x * x, dim=1)
loss = -0.5 * norm.mean()
# regularizer
reg_loss = 0.25 * F.mse_loss(
weight.T @ weight, torch.eye(m), reduction='sum'
)
loss = loss + lambd * reg_loss
# update weight
loss.backward()
optimizer.step()
optimizer.zero_grad()
t2 = time.time()
# log
log['time'].append(t2 - t1)
log['epoch'].append(i)
log['lr'].append(scheduler.get_last_lr())
with torch.no_grad():
dot = A @ weight
objective = torch.sum(dot * dot, dim=1).mean()
reg = F.mse_loss(
weight.T @ weight, torch.eye(m), reduction='sum'
)
log['loss'].append(objective.item())
log['reg_loss'].append(reg.item())
# update scheduler
scheduler.step()
正則化パラメータ lambd を 10, 100, momentum を 0, 0.5 と変えて実験を行う。
実験結果は以下の通り。
左が制約条件からの乖離、右が目的関数の値と最適値 (破線) を示している (横軸は計算時間)。
この結果から、regularizer-based method は正則化パラメータの影響を大きく受けること、最適値 (破線) よりも大きい値に収束しており、直交制約を十分に満たせていないことがわかる。

Retraction-based Method
はじめに、リーマン多様体上の最適化についてはいくつかの Qiita 記事がある。
リーマン多様体上の最適化手法 (retraction, vector transport など) を用いて、直交制約 $X^\top X=I_{m\times m}$ を満たしながら変数を更新する手法が下記の ICLR2020 の論文で提案されている。
この論文では、Cayley retraction と呼ばれる retraction が用いられている。
他にも、polar retraction や QR retraction などの retraction が Stiefel 多様体に対して用いられる。(参考: Projection Robust Wasserstein Distance and Riemannian Optimization の supplemental)
これらの Stiefel 多様体上の最適化手法の PyTorch の実装は、サーベイ論文によると以下の二つのリポジトリが有用らしい。
- GitHub - mctorch/mctorch: A manifold optimization library for deep learning
- GitHub - geoopt/geoopt: Riemannian Adaptive Optimization Methods with pytorch optim
McTorch は2021年で更新が止まっているため、本記事では geoopt を用いて Stiefel 多様体上での最適化を実装する。
geoopt では、重みを ManifoldParameter でラップし、RiemannianSGD を使用することで、リーマン多様体上の最適化を適用することができる。
なお、geoopt は pip install geoopt でインストールできる。
import geoopt
from geoopt.manifolds import Stiefel
from geoopt.optim import RiemannianSGD
# initialize using ManifoldParameter
set_random_seed(42)
weight = init_weight(n, m).requires_grad_(True)
# set `canonical=False` to use QR retraction
weight = geoopt.ManifoldParameter(weight, manifold=Stiefel(canonical=False))
# dataloader
batch_size = 128
dataloader = DataLoader(A, batch_size=batch_size, shuffle=True)
# Riemannian optimizer
momentum = 0.
lr = 0.002
step_size = 30
gamma = 0.1
optimizer = RiemannianSGD([weight], lr=lr, momentum=momentum)
scheduler = torch.optim.lr_scheduler.StepLR(
optimizer, step_size=step_size, gamma=gamma
)
# train loop
epochs = 60
log = dict(time=[], epoch=[], lr=[], loss=[], reg_loss=[])
for i in trange(epochs):
for x in dataloader:
if x.shape[0] < batch_size:
continue
t1 = time.time()
# objective function
x = x @ weight
norm = torch.sum(x * x, dim=1)
loss = -0.5 * norm.mean()
# update weight
loss.backward()
optimizer.step()
optimizer.zero_grad()
t2 = time.time()
# log
log['time'].append(t2 - t1)
log['epoch'].append(i)
log['lr'].append(scheduler.get_last_lr())
with torch.no_grad():
dot = A @ weight
objective = torch.sum(dot * dot, dim=1).mean()
reg = F.mse_loss(
weight.T @ weight, torch.eye(m), reduction='sum'
)
log['loss'].append(objective.item())
log['reg_loss'].append(reg.item())
# update scheduler
scheduler.step()
momentum を 0, 0.5 と変えて実験を行う。
実験結果は以下の通り。
Regularizer-based のものと比較して、制約条件を満たせている代わりに計算時間が3倍以上に膨れ上がっていることがわかる。
また、momentum を使用した手法は最適値付近に収束している。

2023年の研究
Stiefel 多様体上の Retraction の計算量の大きさを回避するための研究がなされている。
- Infeasible Deterministic, Stochastic, and Variance-Reduction Algorithms for Optimization under Orthogonality Constraints
- Momentum Stiefel Optimizer, with Applications to Suitably-Orthogonal Attention, and Optimal Transport
二本目の論文については実装があるため、簡単に試すことができる。
まず、GitHub から StiefelOptimizers.py と utils_StiefelOptimizers.py をダウンロードする。
あとは以下のようにパラメータを Euclidean と Stiefel で分ければ良いらしい。
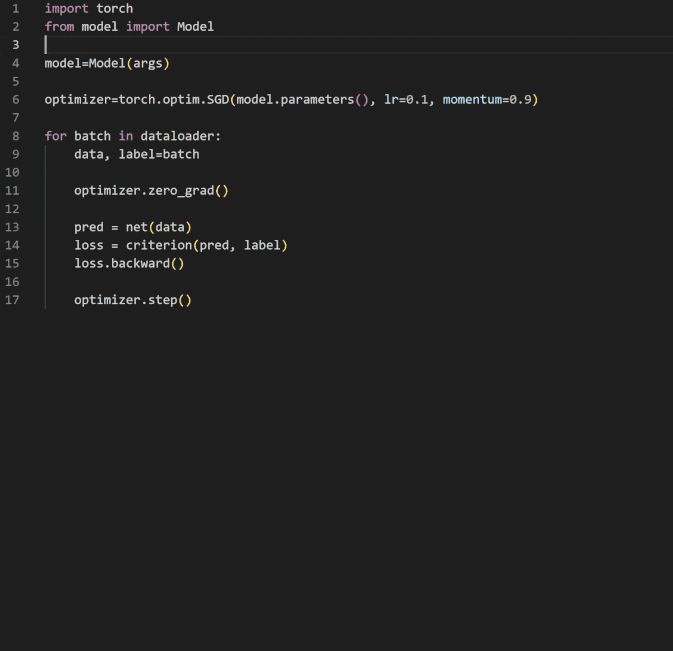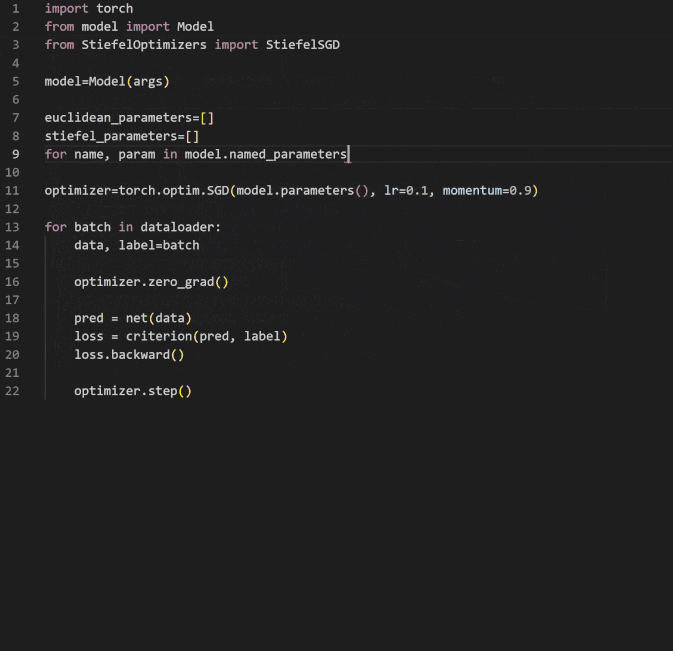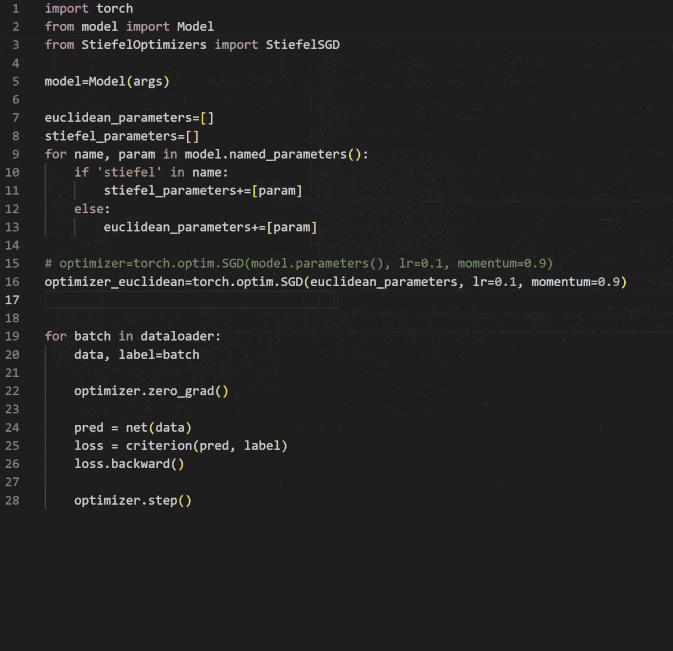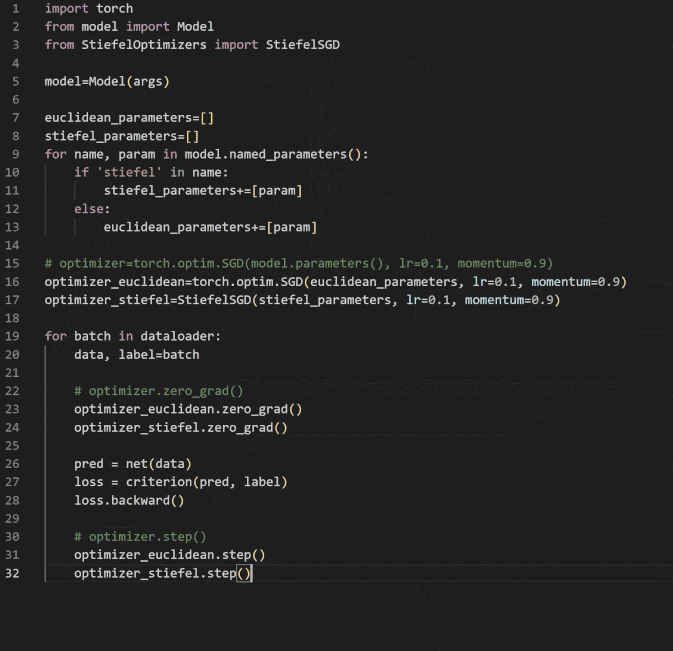
今回は、変数が Stiefel 多様体上のみなため、特に変数を分離する必要はない。
from StiefelOptimizers import StiefelSGD
# initialize
set_random_seed(42)
weight = init_weight(n, m).requires_grad_(True)
# dataloader
batch_size = 128
dataloader = DataLoader(A, batch_size=batch_size, shuffle=True)
# Stiefel optimizer
momentum = 0.
lr = 0.002
step_size = 30
gamma = 0.1
optimizer = StiefelSGD([weight], lr=lr, momentum=momentum)
scheduler = torch.optim.lr_scheduler.StepLR(
optimizer, step_size=step_size, gamma=gamma
)
# train loop
epochs = 60
log = dict(time=[], epoch=[], lr=[], loss=[], reg_loss=[])
for i in trange(epochs):
for x in dataloader:
if x.shape[0] < batch_size:
continue
t1 = time.time()
# objective
x = x @ weight
norm = torch.sum(x * x, dim=1)
loss = -0.5 * norm.mean()
# update weight
loss.backward()
optimizer.step()
optimizer.zero_grad()
t2 = time.time()
# log
log['time'].append(t2 - t1)
log['epoch'].append(i)
log['lr'].append(scheduler.get_last_lr())
with torch.no_grad():
dot = A @ weight
objective = torch.sum(dot * dot, dim=1).mean()
reg = F.mse_loss(
weight.T @ weight, torch.eye(m), reduction='sum'
)
log['loss'].append(objective.item())
log['reg_loss'].append(reg.item())
# update scheduler
scheduler.step()
momentum を 0, 0.5 と変えて実験を行う。
実験結果は以下の通り。
Momentum Stiefel optimizer (図中 ssgd) を用いると、制約条件を満たしたまま、QR retraction (図中 rsgd) よりも高速に計算できていることがわかる。

終わりに
本記事では PyTorch を用いて Stiefel 多様体上で最適化を行う方法を調査した。
最後に紹介した momentum Stiefel optimizer は ICLR2023 の論文であり、リー群での momentum SGD の論文の後継である。
これらの研究は Nesterov Accelerated Gradient descent (NAG) の変分問題 (variational problem) による一般化の論文を拡張したものになっている。
Nesterov の加速法については、例えば 鈴木大慈先生の講義資料 の p.36 あたりが参考になる。
加速法と常微分方程式の関係については以下の資料が参考になる? (常微分方程式に詳しくないため理解していない)
また、momentum Stiefel optimizer の論文は vision transformer への応用を数値実験で行い、その有用性を確認している。
具体的には、multihead attention の各ヘッドのアテンション $\mathop{\mathrm{Attention}}\left(QW_i^Q,KW_i^K,VW_i^V\right)$ の $W_i^Q, W_i^K$ に直交制約を課すことで、CIFAR に対するスクラッチ学習の精度が向上したことを報告している。

今後、深層学習モデルについて、重みの直交性が重要な役割を担うかもしれない。