はじめに
この記事はLiNGAMの高速化を実装したものに加え、いくつかの拡張を行ったものです。
概要
統計的因果探索手法にLinear non-Gaussian Acyclic Model(LiNGAM)という手法があります。
これは下記仮定の下で因果関係を推定することができます。(仮定については条件付きで緩和が進められている)
- 未観測共通原因が存在しない
- 有向非巡回モデルである
- 各変数が連続変数である
- 各変数の誤差項は非ガウス分布に従う
- 各変数の関係は線形である
因果関係は下記構造方程式の$\boldsymbol{B}$を推定することで実現します。
$$\boldsymbol{x} = \boldsymbol{B}\boldsymbol{x} + \boldsymbol{e}$$
$\boldsymbol{B}$はICA(独立成分分析)による混合行列を上記仮定を用いて一意に特定します。
$\boldsymbol{B}$は仮定より、正しい因果関係で置換すれば上三角部分が0となります。
しかし、実際にICAと仮定によって得られる推定行列は、要素に0に近い値を持った$\boldsymbol{\hat{B}}$です。
ここから$\boldsymbol{B}$を推定するには、$\boldsymbol{P}$$\boldsymbol{\hat{B}}$$\boldsymbol{P}^T$の上三角部分が最小となるような置換行列$\boldsymbol{P}$を求めるという手法を取ります。
MLPシリーズの統計的因果探索(http://bookclub.kodansha.co.jp/product?isbn=9784061529250)
現状
Pythonライブラリはありませんでしたが既に実装されている方がいました。
https://qiita.com/ragAgar/items/131b17171b93f63d6475
問題
記事を書くに至る動機でもありますが、上記コードを用いて実データに適用して分析を進めていたところ、ある問題に直面しました。
-
メモリオーバー
推定に必要な置換行列のパターンを一度にすべて展開している為、多量のメモリを消費している。 -
次元数Nによる計算オーダーの爆発的増加
計算にO(N!)レベルのコストがかかっているため、ある程度から現実的な計算コストを超えてしまう。
1についてはコードを書き直せば解決しますが、2についてはアルゴリズムレベルでの再実装が必要です。
2についてはMLPシリーズの統計的因果探索にも下記のような言及があります。
ただし、観測変数の数が増えるにつれて、このような置換行列を探すことは現実的には不可能になります。
ありうる置換行列の数が膨大になり、すべての置換行列の候補を試すことができなくなってしまうからです。
ここでいう探索はグリッドサーチです。Sequential Based Model Optimizationのようなベイズ的探索を行えば計算量を落とせるのでは?と思いましたが、置換行列を構成するパターンについて損失を最適化することは難しいので却下しました。
高速化のためには置換行列によるアプローチから脱却する必要があります。これについても同書籍に下記記載があります。
そこで、すべての置換行列の候補を試すことを回避するような方法が提案されています[参考文献]。
今回はこの参考文献のアルゴリズムを実装しました。
高速化アルゴリズム
New permutation algorithms for causal discovery using ICA
https://pdfs.semanticscholar.org/c9ce/692644189055ccd98a572d0be7f3d48bcca9.pdf
詳細は上記論文を読んで頂いた方が良いと思いますが、一言でかみ砕いていえば、
正しい因果順序へ変換すれば$\boldsymbol{B}$は上三角部分が0になるということは、
ある変換により三角化可能となるまで$\boldsymbol{\hat{B}}$の要素のうち0に近い部分から0に置き換えていけば、$\boldsymbol{\hat{B}}$から$\boldsymbol{B}$を推定できるのではないか、という事です。
高速化アルゴリズムに加えて追記した内容
-
推定した構造モデルの残差が正規分布に従っているかどうか
⇒ 念のためチェックできるようにShapiro Wilk検定を出来るように実装。 -
すべての係数行列を表示していては煩雑な場合があろうのでないか
⇒ 回帰についてLinearRegressionとLassoRegressionを選択可能に拡張。 -
グラフィカルにみたい
⇒ graphvizによる可視化を追加。
実施検証
from numpy.random import *
size=1000
a = 3
b = -2
c = 2
np.random.seed(2017)
x = np.random.uniform(size=size)
np.random.seed(1028)
y = a * x + b*1 + beta(15,5, size=size)
np.random.seed(1028)
z = c * y + beta(15,5, size=size)
u = np.random.normal(10,2, size=size)
X = pd.DataFrame(np.asarray([x, y, z, u]).T,
columns=["x", "y", "z", "u"])
lingam = LiNGAM()
lingam.fit(X, max_iter=800, reg_type="linear", algorithm="normal", shapiro=True)
lingam.visualize()
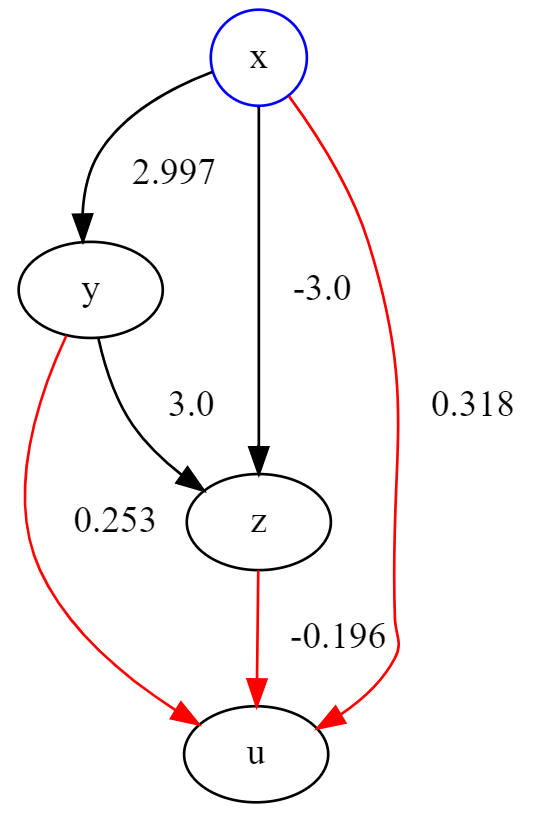
lingam = LiNGAM()
lingam.fit(X, max_iter=800, reg_type="linear", algorithm="fast", shapiro=True)
lingam.visualize()

簡単なモデルなので推定結果は同じになっていますが、手法上、毎回結果が異なるので因果関係も変わる場合があります。
Shapiro Wilk検定によればuの誤差項が正規分布であることがわかります。
uに対する結果はあまり信頼しない方が良いという見方もできると思います。
lingam = LiNGAM()
lingam.fit(X, max_iter=800, reg_type="lasso", algorithm="fast", shapiro=True)
lingam.visualize()
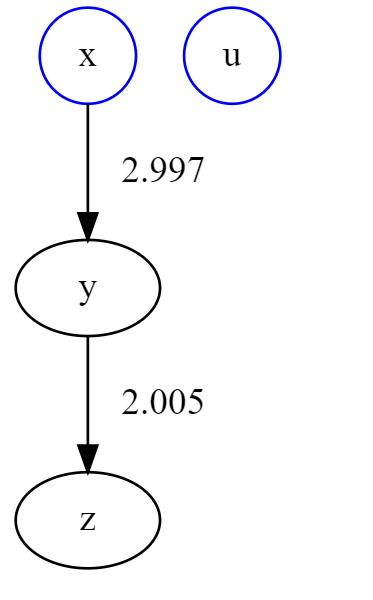
随分と簡素化されました。
比較的大きいモデルについては枝切りをした方が見やすいです。
考察
実際どのくらい速くなったのかというと、10変数程度で30分程かかる計算が数秒で完了します。
詳細も上記の論文に記載されているので気になる方は参照して下さい。
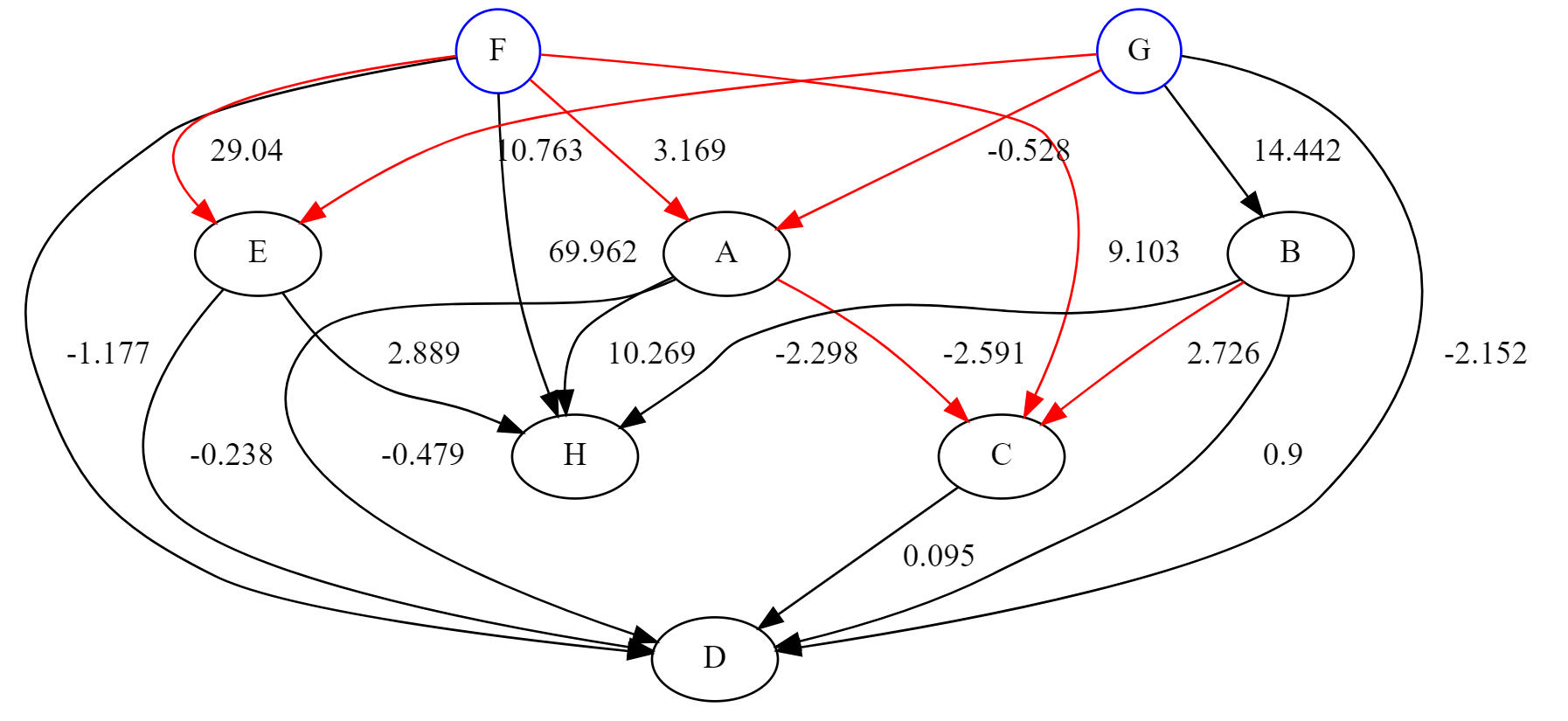
実データへの適用
実データに適用した結果を掲載します。
変数名は公開できないのでアルファベットに置き換えています。
このようにデータの構造がある程度把握できると、入力と出力の関係を用いてモデル構築や異常検知にも役立てることができます。
おわりに
LiNGAMは仮定が多いものの、因果関係を推定できるというのは強いです。
しかし実データに対して利用するとなると仮定が成り立つことを確認することは難しいです。
それに対して同書籍に下記の記述があります。
因果効果の予測が目的の場合、因果グラフの推測にいくらか誤りが含まれていても、因果効果の予測がうまく行けば、それで十分だという考え方もあるでしょう。
これについては私も同意見ですし、LiNGAMに限らず言えることでもあると思います。
例えばLiNGAMに対して非線形構造のデータを入れてみて、どの程度まで対応することができるか検証することは興味深いと思います。
詳細は掲載しませんが、指数関係、交互作用等、ある程度の非線形性に対しては係数等によりますが因果関係自体は推定できます。
下記にコードを公開します。
https://github.com/NibuTake/LiNGAM-fast
以上です。