LoginSignup
16
12

More than 5 years have passed since last update.

@MomonekoView

RNN モデルを Python で実装して簡単な数列を解かせてみた。

Last updated at Posted at 2018-10-08

【背景】

　本稿はゲートユニットの無い単純なリカレントニューラル (RNN) に焦点を当てている。多層ニューラルネットワーク (DNN) や畳み込みニューラルネットワーク (CNN) には，手書き文字認識の MNIST という有名なデータセットがあるが，RNN では MNIST に相当するようなデータセットが無く，オープンソースにもコードの簡単な例が少ないので、今回足し算と引き算を交互に繰り返す簡単な数列をデータとして用い，python で書いた RNN モデルに解かせてみた。
(ソースコード github, https://github.com/MomonekoView/RNN_for_Progression)

環境:
Python 3.4.5
Windows 10 or Linux 16.04

【RNN 概要】

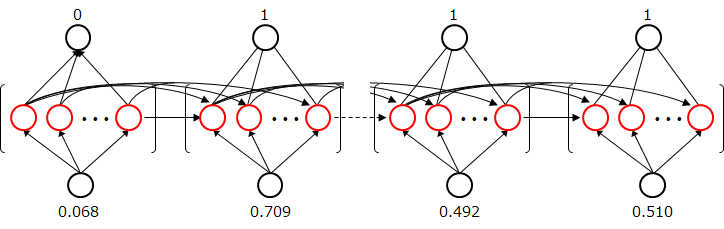
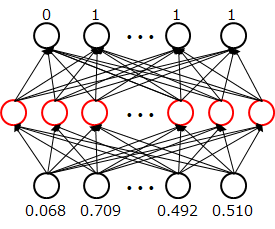
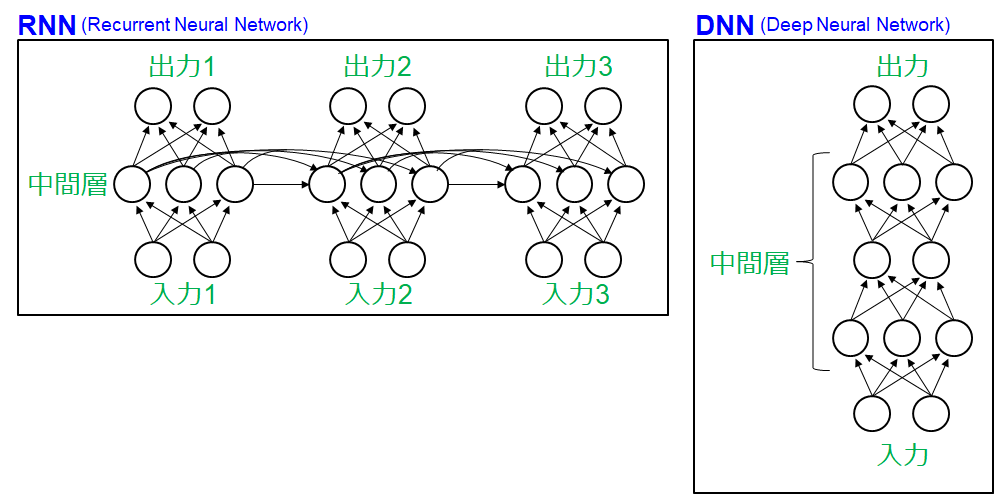
　RNN の構造を DNN と比較して下記に示す。DNN ではすべての入力データが同時に処理され出力されるのに対し，RNN では入力が分割されて順番に処理される。中間層どおしは連結されており，ある時点の計算は過去の中間層の出力の影響を受ける。 (必ずしも全中間層に入出力が割り当てられる必要は無く，one to many, many to one などさまざまなタイプが提案されている (参照 1)) 。どの時点においても 3 種類の重み (入力から中間層，中間層から中間層，中間層から出力層) にそれぞれ同じ値が使われまた，中間層から中間層への対応は総当たりで重み結合される。

【学習データについて】

　RNN で扱うデータは，ある情報が連続して配置されることで意味を成すデータ (言語や音声はもちろん，天気予報や店舗の集客記録，株価など) が適していると言われているが，画像認識における MNIST や cifar10 のような，量と使い勝手の良い汎用的なものはあまり見当たらない。今回は，下図に示すような数列を入出力とした。まず，0～1 の乱数 8 個からなる配列を入力とし，端から足し算と引き算と交互に繰り返す。得られた各要素の値が 0 以上なら 0 とし, 0 より小さければ 1 とする配列を出力とした。

Python でのデータ生成コード。

functions.py
def random_seq(x):
    ans = 0
    sign = []
    for i in range(len(x)):
        if i%2 == 0:
            ans += x[i]
        else:
            ans -= x[i]
        if ans >= 0:
            sign.append(1)
        else:
            sign.append(0)
    return ans, sign
rnn.py
sequence_length = 8
x_train = []
y_train = []
for j in range(50000):   #5万個の教師データを生成
    data = np.random.rand(sequence_length)
    _, val = random_seq(data)
    x_train.append(data)
    y_train.append(val)

【RNN 学習モデルについて】

生成した数列データを RNN および比較対象として DNN で学習させた。
（DNN では中間層を 1 層としたため，厳密には Deep ではないが）
入出力データとモデルとの対応は下記のようになる。数字は上記の配列例に対応している。

・RNN
Fig_4.png

・DNN
Fig_3.png

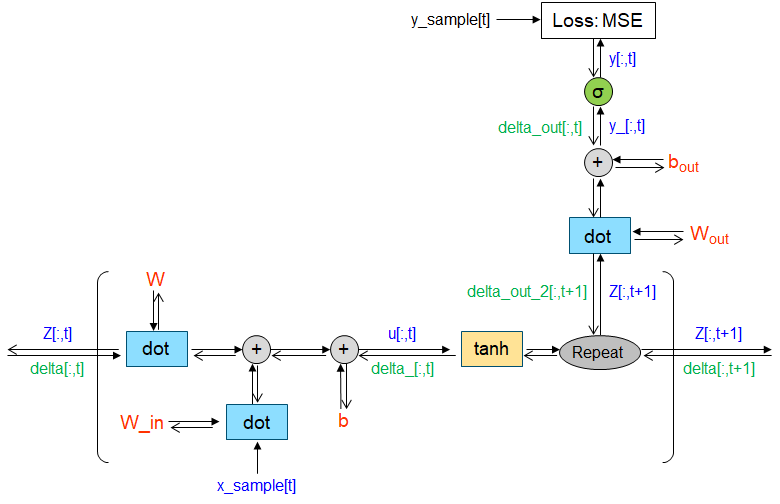
それぞれプログラムと対応する計算グラフの詳細は下記。
作成に当たっては，参照 (2, 3) を参考にしながら適宜組み替え行った。

・RNN

rnn.py
# -*- coding: utf-8 -*- 

import numpy as np
from functions import *
import matplotlib.pyplot as plt
import pandas as pd
import pickle

##### モデル設定 #####
sequence_length = 8
input_layer_size = 1
hidden_layer_size = 100
output_layer_size = 1

# 学習率設定
learning_rate = 0.1

iters_num = 20000
plot_interval = 500

# 重み行列とバイアスの設定
params = {}
params['W_in'] = np.random.randn(input_layer_size, hidden_layer_size)/(np.sqrt(input_layer_size))
params['W_out'] = np.random.randn(hidden_layer_size, output_layer_size)/(np.sqrt(hidden_layer_size))
params['W'] = np.random.randn(hidden_layer_size, hidden_layer_size)/(np.sqrt(hidden_layer_size))
params['b'] = np.zeros(hidden_layer_size)
params['b_out'] = np.zeros(output_layer_size)

# 勾配の設定
W_in_grad = np.zeros_like(params['W_in'])
W_out_grad = np.zeros_like(params['W_out'])
W_grad = np.zeros_like(params['W'])
W_b_grad = np.zeros_like(params['b'])
W_b_out_grad = np.zeros_like(params['b_out'])

# ※1　各時系列におけるデータの格納 
u = np.zeros((hidden_layer_size, sequence_length)) 
z = np.zeros((hidden_layer_size, sequence_length + 1)) # ※3 回帰的な内部状態。BPTTが計算できるよう、1を足しておく。
y_ = np.zeros((output_layer_size, sequence_length))
y = np.zeros((output_layer_size, sequence_length))

# ※2
delta_out = np.zeros((output_layer_size, sequence_length))
delta_out_2 = np.zeros((hidden_layer_size, sequence_length + 1)) # ※4
delta_ = np.zeros((hidden_layer_size, sequence_length)) 
delta = np.zeros((hidden_layer_size, sequence_length + 1)) # ※3 z と同様に BPTTが計算できるよう、1を足しておく。

#結果データ格納リスト
accuracy_list = []

##### 教師データ作成 #####
x_train = []
y_train = []

for j in range(50000):
    data = np.random.rand(sequence_length)
    _, val = random_seq(data)
    x_train.append(data)
    y_train.append(val)

x_train = np.array(x_train)
y_train = np.array(y_train)

##### トレーニング #####
for i in range(iters_num):
    choice = np.random.choice(len(x_train), 1) # バッチサイズ1で逐次的に処理
    x_sample = x_train[int(choice)]
    y_sample = y_train[int(choice)]

    # 時系列ループ
    for t in range(sequence_length):

        u[:,t] = np.dot(x_sample[t].reshape(1, -1), params['W_in']) + np.dot(z[:,t].reshape(1, -1), params['W']) + params['b']
        z[:,t+1] = np.tanh(u[:,t])
        y_[:,t] = np.dot(z[:,t+1].reshape(1, -1), params['W_out']) + params['b_out']
        y[:,t] = sigmoid(y_[:,t])
        loss = least_square(y[:,t], y_sample[t])

    #Backward
    for t in range(sequence_length)[::-1]:
        delta_out[:,t] = (y[:,t] - y_sample[t]) * (1-y[:,t])*y[:,t]
        delta_out_2[:,t+1] = np.dot(delta_out[:,t].reshape(1,-1), params['W_out'].T)
        delta_[:,t] = (delta_out_2[:,t+1] + delta[:, t+1]) * d_tanh(u[:,t])
        delta[:,t] = np.dot(delta_[:,t], params['W'].T)

        # 各 t において勾配の値を蓄積する ※5
        W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(1,-1))
        W_b_out_grad += np.sum(delta_out[:,t].reshape(1,-1), axis = 0)
        W_grad += np.dot(z[:,t].reshape(-1,1), delta_[:,t].reshape(1,-1))
        W_in_grad += np.dot(x_sample[t].reshape(-1, 1), delta_[:,t].reshape(1,-1))
        W_b_grad += np.sum(delta_[:,t].reshape(1,-1), axis = 0)

    #出力を 0 or 1 に変換する ※6
    for j in range(len(y[0])):
        if y[:,j] >= 0.5:
            y[:,j] = 1
        else:
            y[:,j] = 0

    # 勾配の更新 ※7
    params['W_in'] -= learning_rate * W_in_grad
    params['W_out'] -= learning_rate * W_out_grad
    params['W'] -= 0.001 * W_grad
    params['b_out'] -= learning_rate * W_b_out_grad
    params['b'] -= 0.001 * W_b_grad

    W_in_grad *= 0
    W_out_grad *= 0
    W_grad *= 0
    W_b_out_grad *= 0
    W_b_grad *= 0

    ##### 正答率算出 ##### ※8
    count = 0
    if(i % plot_interval == 1):
        print("iters:" + str(i))
        acc = 0
        for k in range(len(y[0,:])):
            acc += np.sum(y[0,k] == y_sample[k])
        print('y', y[0,:])
        print('y_sample', y_sample)
        print('accuracy', acc)
        accuracy_list.append(acc)
        count = 0

Fig_6.png

※1 中間層と出力において，データを格納する変数 (u, z, y_, y) を事前に設定しておく。
※2 逆伝播においても同様に，データを格納する変数 (delta_out, delta_out_2, delta_, delta) を事前に設定。
※3 z と delta については，逆伝播で sequence_length + 1 (ここでは 9) の時点から値 (ゼロ) を計算に使う必要があるので，サイズを 1 つ大きくしておく。
※4 delta_out_2 については，順伝播の z と対応させるため同様にサイズを 1 つ大きく設定。
※5 RNN では各時刻における重みは共通なので，勾配は加算しておいてまとめて更新する。
※6 出力層のシグモイドユニットの値に敷居 (0.5) を設け，1 or 0 に変換。
※7 学習率の設定： 繰り返しで演算がかかる中間層の W と b は，入出力のパラメータよりも学習率を小さめで設定した方が，学習がぶれずに収束が緩やかとなる。
※8 一定回数ごとに，8 個の配列要素からなる出力に対して，正答している要素の数を accuracy として出力。

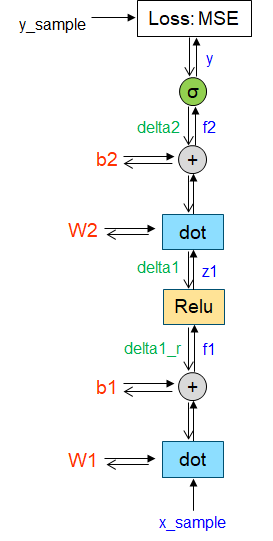
・DNN

dnn.py
# -*- coding: utf-8 -*- 

import numpy as np
from functions import *
import matplotlib.pyplot as plt
import pandas as pd
import pickle

##### モデル設定 #####
input_layer_size = 8
hidden_layer_size = 100
output_layer_size = input_layer_size

#学習率設定
learning_rate = 0.1

iteration = 20000
plot_interval = 500

# 重み行列とバイアスの設定
params = {}
params["W1"] = np.random.randn(input_layer_size, hidden_layer_size)/np.sqrt(input_layer_size)
params["b1"] = np.random.randn(hidden_layer_size)
params["W2"] = np.random.randn(hidden_layer_size, output_layer_size)/np.sqrt(hidden_layer_size)
params["b2"] = np.random.randn(output_layer_size)

#順伝播
def forward(params, x):
    W1, W2 = params["W1"], params["W2"]
    b1, b2 = params["b1"], params["b2"]
    f1 = np.dot(x, W1) + b1
    z1 = relu(f1)
    f2 = np.dot(z1, W2) + b2
    y  = sigmoid(f2)
    return z1, y

#逆伝播
def backward(params, x, z1, y):
    grad = {}
    W1, W2 = params["W1"], params["W2"]
    b1, b2 = params["b1"], params["b2"]
    delta2 = d_least_square(y, y_sample)*(1-y)*y
    grad["b2"] = np.sum(delta2, axis = 0)   
    grad["W2"] = np.dot(z1.reshape(-1, 1), delta2) 
    delta1 = np.dot(delta2, W2.T)               
    delta1_r = delta1*d_relu(z1)  
    grad["b1"] = np.sum(delta1_r, axis = 0) 
    grad["W1"] = np.dot(x.reshape(-1, 1), delta1_r)
    return grad

#結果データ格納リスト
accuracy_list = []


##### 教師データ作成 #####
x_train = []
y_train = []

for j in range(50000):
    data = np.random.rand(input_layer_size)
    _, val = random_seq(data)
    x_train.append(data)
    y_train.append(val)

x_train = np.array(x_train)
y_train = np.array(y_train)

##### トレーニング #####
for i in range(iteration):
    choice = np.random.choice(len(x_train), 1) # バッチサイズ1で逐次的にs処理
    x_sample = x_train[int(choice)]
    y_sample = y_train[int(choice)]

    z1, y = forward(params, x_sample)
    y_sample = y_sample.reshape(1, -1)     # ベクトル形式を(1,)から(1, 1)へ再定義
    loss = least_square(y_sample, y)       # ロス関数として、誤差二乗平均を使用
    grad = backward(params, x_sample, z1, y)

    #出力を 0 or 1 に変換する
    for j in range(len(y)):
        if y[j] >= 0.5:
            y[j] = 1
        else:
            y[j] = 0

    # 勾配の更新
    for key in ("W1", "W2", "b1", "b2"):
        params[key] -= learning_rate * grad[key]

    ##### 正答率算出 #####
    count = 0
    if(i % plot_interval == 1):
        print("iters:" + str(i))
        acc = 0
        for k in range(len(y)):
            acc += np.sum(y[k] == y_sample[0,k])
        print('y', y)
        print('y_sample', y_sample[0,:])
        print('accuracy', acc)
        accuracy_list.append(acc)
        count = 0

Fig_5.png

ノード数を RNN と同じ 100 とした。 シグモイド出力を 1 or 0 へ変換。
一定回数 (500回) ごとに RNN と同じ基準で正答数を出力。2 万回まで学習を実施した。
また，データ長の影響を見るため，入出力データの要素数を 8, 16, 32 と伸ばして評価した。

【結果】

・配列の要素数: 8

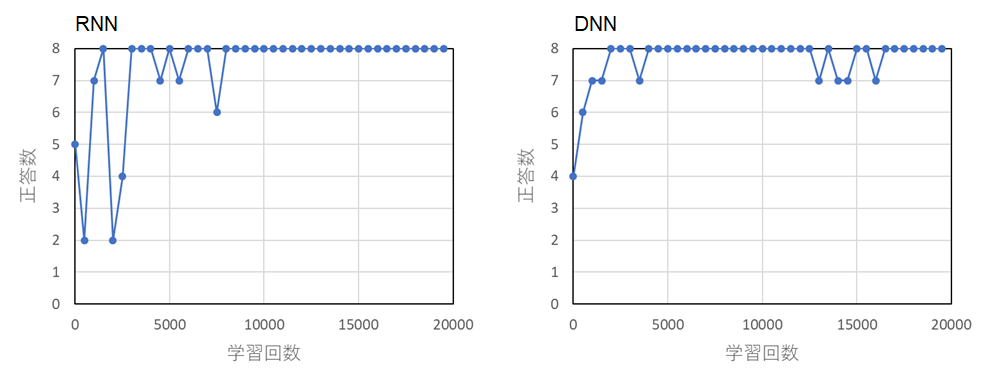
　両者において，学習とともに正答数が上昇し，iteration 3000 ～ 5000 回で正答数が飽和しているように見える。

・配列の要素数: 16

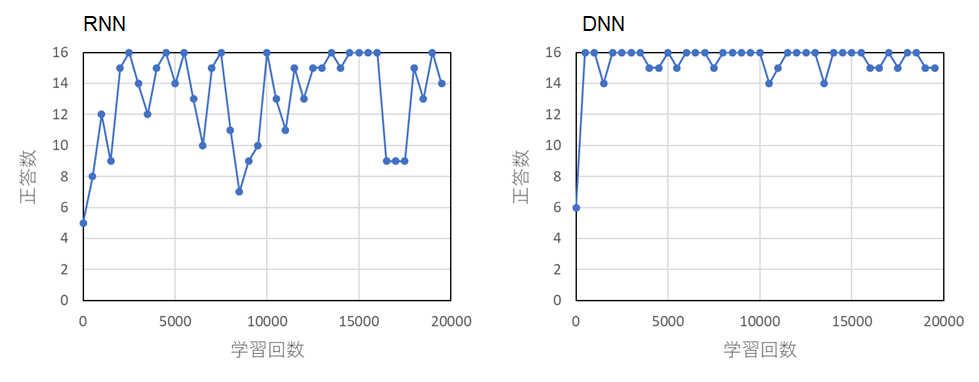
・配列の要素数: 32

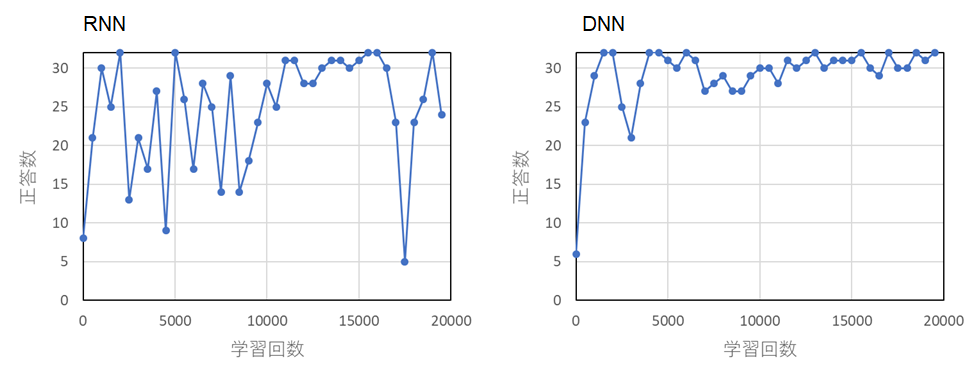
　RNN では要素数が多くなるにつれて学習がうまく進まないことがわかる。これは，中間層のパラメータの勾配がゼロに収束 (勾配消失)，あるいは勾配爆発が起きてしまったためと思われる。これに対し，DNN では多少のブレはあるが，要素数増に関わらず学習が進行した。
　データ長が長くなると RNN の学習が進まなくなることはよく知られた現象であり，今回それを確認できたと言える (改善するためには，ゲート構造を導入したり勾配クリッピングを用いる必要がある)。一方，今回用いた DNN が単純なアーキテクチャーに関わらず，それなりに学習できたのが少し意外であった。CNN で文が解析できるなどの既報はあり(参照 4)，今回のデータのように長期の相関の無い単純なものについては，DNN で十分に学習可能であったと思われる。

【参照】

1) リカレントニューラルネットワークの理不尽な効力（翻訳），https://qiita.com/KojiOhki/items/397f157342e0def06a9b
2) ゼロから作る Deep Learning ②　自然言語処理編，斎藤 康毅 著，O'REILLY
3) RNN と LSTM の基礎，丸山 不二夫, crash.academy, https://crash.academy/video/66/359
4) Convolutional Neural Networks for Sentence Classification, Y. Kim, EMNLP, 2014, https://arxiv.org/abs/1408.5882

16
12
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
16
12