1. 背景
以前、Euler法を用いて一階常微分方程式を解いた。(記事はこちら)
Julia には、あらゆる種類の微分方程式を解くための準備がされている。(公式doc.はこちら)
この記事では、一階常微分方程式をODEProblemを用いて簡単に解いていこう。
#2. 準備
以下の手順に従っていこう。
2.1 パッケージを導入する
ODEProblemを使うには、パッケージDifferentialEquationsを追加する必要がある。
以下のようにTerminalで実行していこう。
Terminal
$ julia
_
_ _ _(_)_ | Documentation: https://docs.julialang.org
(_) | (_) (_) |
_ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 1.2.0 (2019-08-20)
_/ |\__'_|_|_|\__'_| | Official https://julialang.org/ release
|__/ |
julia> import Pkg
julia> Pkg.add("DifferentialEquations")
Updating registry at `~/.julia/registries/General`
Updating git-repo `https://github.com/JuliaRegistries/General.git`
Resolving package versions...
Installed Parameters ─────── v0.11.0
Installed Sundials ───────── v3.7.0
Installed StochasticDiffEq ─ v6.9.1
Installed OrdinaryDiffEq ─── v5.15.1
Updating `~/.julia/environments/v1.2/Project.toml`
[0c46a032] + DifferentialEquations v6.6.0
Updating `~/.julia/environments/v1.2/Manifest.toml`
[79e6a3ab] + Adapt v1.0.0
[ec485272] + ArnoldiMethod v0.0.4
[4fba245c] + ArrayInterface v1.2.1
[aae01518] + BandedMatrices v0.10.1
[9e28174c] + BinDeps v0.8.10
[8e7c35d0] + BlockArrays v0.9.1
[ffab5731] + BlockBandedMatrices v0.4.6
[764a87c0] + BoundaryValueDiffEq v2.3.0
[49dc2e85] + Calculus v0.5.0
[bbf7d656] + CommonSubexpressions v0.2.0
[bcd4f6db] + DelayDiffEq v5.14.0
[2b5f629d] + DiffEqBase v5.20.1
[459566f4] + DiffEqCallbacks v2.8.0
[01453d9d] + DiffEqDiffTools v1.3.0
[5a0ffddc] + DiffEqFinancial v2.1.0
[c894b116] + DiffEqJump v6.2.1
[77a26b50] + DiffEqNoiseProcess v3.3.1
[055956cb] + DiffEqPhysics v3.2.0
[163ba53b] + DiffResults v0.0.4
[b552c78f] + DiffRules v0.0.10
[0c46a032] + DifferentialEquations v6.6.0
[c619ae07] + DimensionalPlotRecipes v0.2.0
[ffbed154] + DocStringExtensions v0.8.0
[d4d017d3] + ExponentialUtilities v1.5.1
[1a297f60] + FillArrays v0.6.4
[f6369f11] + ForwardDiff v0.10.3
[069b7b12] + FunctionWrappers v1.0.0
[01680d73] + GenericSVD v0.2.1
[d25df0c9] + Inflate v0.1.1
[42fd0dbc] + IterativeSolvers v0.8.1
[82899510] + IteratorInterfaceExtensions v1.0.0
[5078a376] + LazyArrays v0.10.0
[093fc24a] + LightGraphs v1.3.0
[d3d80556] + LineSearches v7.0.1
[a3b82374] + MatrixFactorizations v0.1.0
[46d2c3a1] + MuladdMacro v0.2.1
[f9640e96] + MultiScaleArrays v1.5.0
[d41bc354] + NLSolversBase v7.4.1
[2774e3e8] + NLsolve v4.1.0
[1dea7af3] + OrdinaryDiffEq v5.15.1
[d96e819e] + Parameters v0.11.0
[e409e4f3] + PoissonRandom v0.4.0
[e6cf234a] + RandomNumbers v1.3.0
[731186ca] + RecursiveArrayTools v1.0.2
[f2c3362d] + RecursiveFactorization v0.1.0
[ae5879a3] + ResettableStacks v0.6.0
[f2b01f46] + Roots v0.8.3
[699a6c99] + SimpleTraits v0.9.0
[47a9eef4] + SparseDiffTools v0.9.0
[276daf66] + SpecialFunctions v0.7.2
[9672c7b4] + SteadyStateDiffEq v1.5.0
[789caeaf] + StochasticDiffEq v6.9.1
[c3572dad] + Sundials v3.7.0
[3783bdb8] + TableTraits v1.0.0
[19fa3120] + VertexSafeGraphs v0.1.0
[4607b0f0] + SuiteSparse
Building Sundials → `~/.julia/packages/Sundials/CRi5j/deps/build.log`
特に問題なければ、無事にパッケージを追加できたことになる。
#3. コードを記述する
この例では、
$$
y' = 3y + 2
$$
を解いていく。以下にコードを書いていくが、公式doc.を真似したものだ。
流れとしては、数値解を解いた後に厳密解を合わせてplotする。
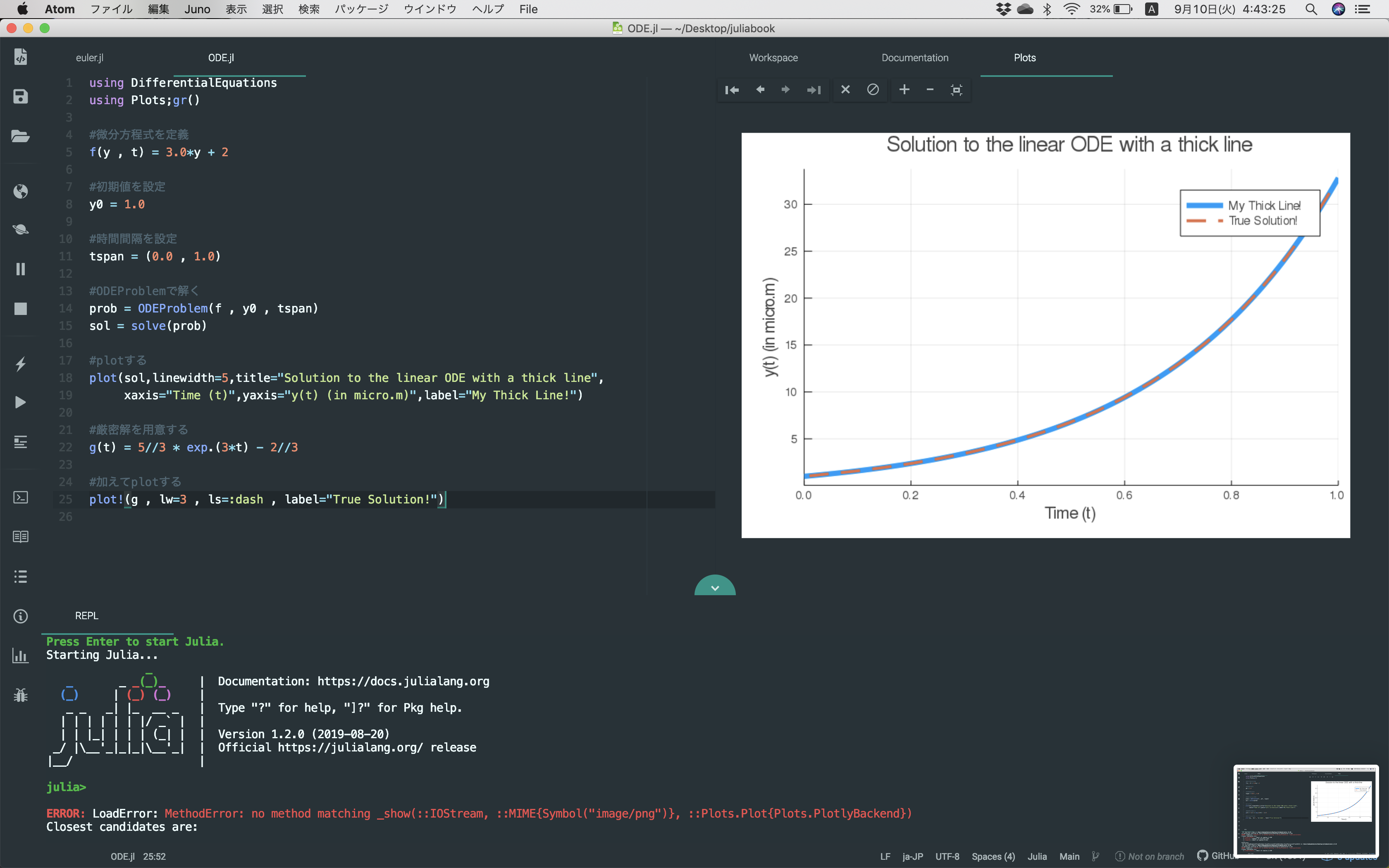
ODE.jl
using DifferentialEquations
using Plots;gr()
#微分方程式を定義
f(y , t) = 3.0*y + 2
#初期値を設定
y0 = 1.0
#時間間隔を設定
tspan = (0.0 , 1.0)
#ODEProblemで解く
prob = ODEProblem(f , y0 , tspan)
sol = solve(prob)
#plotする
plot(sol,linewidth=5,title="Solution to the linear ODE with a thick line",
xaxis="Time (t)",yaxis="y(t) (in micro.m)",label="My Thick Line!")
#厳密解を用意する
g(t) = 5//3 * exp.(3*t) - 2//3
#加えてplotする
plot!(g , lw=3 , ls=:dash , label="True Solution!")
#4. 最後に
Euler法などで記述するよりも簡単に微分方程式を解くことができましたね、文のあらゆるところに公式doc.のリンクを埋めておいたのでいろんな微分方程式を解いてみてね!