1. Euler法 とは
Wikipedia によると、
オイラー法(オイラーほう、英: Euler method) とは、常微分方程式の数値解法の一つである。この方法は、数学的に理解しやすく、プログラム的にも簡単なので、数値解析の初歩的な学習問題としてよく取りあげられる。
しかし、1階段数常微分方程式の数値解法としては誤差が蓄積されるため、精度が悪く、元の微分方程式によってはいかなる h をとっても元の方程式の解に収束しないこともある方法なので、学習目的以外であまり使われない。
ざっくりとEuler法を書くと微分の定義を用いて、
$$
y' = \frac{y(t + \Delta t) - y(t)}{\Delta t}
$$
これを式変形してまとめると、
$$
y(t + \Delta t) = y(t) + y'\Delta t
$$
となる。これをプログラムを書くために配列によって書き表すと
y[n+1] = y[n] + y'*dt
#y'は関数により、Δt = dt と表記する。
誤差は生じれど、数値計算の初歩的な練習には適しているみたいだ。最近私はJuliaでの数値計算を練習したりしているので使ってみよう。(PkgでODEProblemとかあるけど、今回は使わないよ)
より正確に数値計算やるなら改良Euler法とかRunge-Kutta法で解くのが良いかと思います。
2.コードを書くための準備
以下の手順にしたがって準備を進めていこう。
2.1 今回使用する一階線形微分方程式
ここでは、
$$
y' = 3y + 2~~ , ~~y(0) = y_0
$$
を例にする。これをEuler法で考えていく。
2.2 Euler法への落とし込み
- で導入した式に代入すると、
$$
y(t + \Delta t) = y(t) + (3y + 2)\Delta t
$$
自明に $y = y(t)$ であるので、$y(t)$でくくると、
$$
y(t + \Delta t) = (1 + 3\Delta t)y(t) + 2\Delta t
$$
である。この式を、配列によって書き直すと
y[n+1] = (1 + 3*dt)*y[n] + 2*dt
#Δt = dt
である。ここまで準備できれば、ほぼ完成したようなものだろう。
2.3 厳密解も準備しておこう
数値解との比較もしたいので、厳密解も同時にプロットしよう。与えられた微分方程式を微分積分学の知識を用いて解くと、
$$
y(t) = \left(y_0 + \frac{2}{3}\right)e^{3t} - \frac{2}{3}
$$
となる。
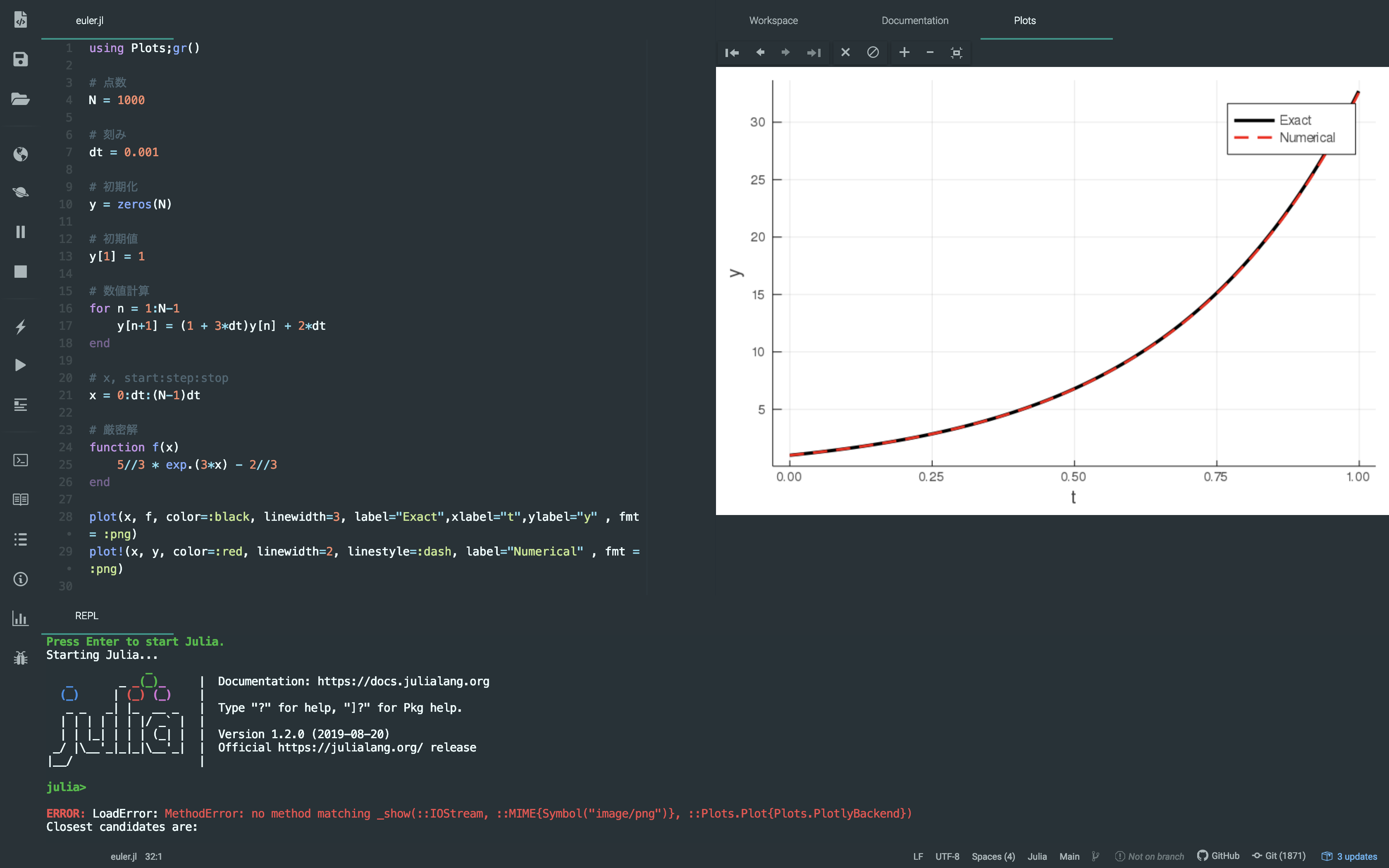
3. コードを記述する
それでは、これまで準備してきたことを使ってコードを記述していこう。
using Plots;gr()
# 点数
N = 1000
# 刻み
dt = 0.001
# 初期化
y = zeros(N)
# 初期値(y(0) = y_0 = 1 とした)
y[1] = 1
# 数値計算
for n = 1:N-1
y[n+1] = (1 + 3*dt)y[n] + 2*dt
end
# x = 開始値:間隔:終了値
x = 0:dt:(N-1)dt
# 厳密解
function f(x)
5//3 * exp.(3*x) - 2//3
end
#色々と指定してplot.
#plot!はグラフを追加する機能をもつ。
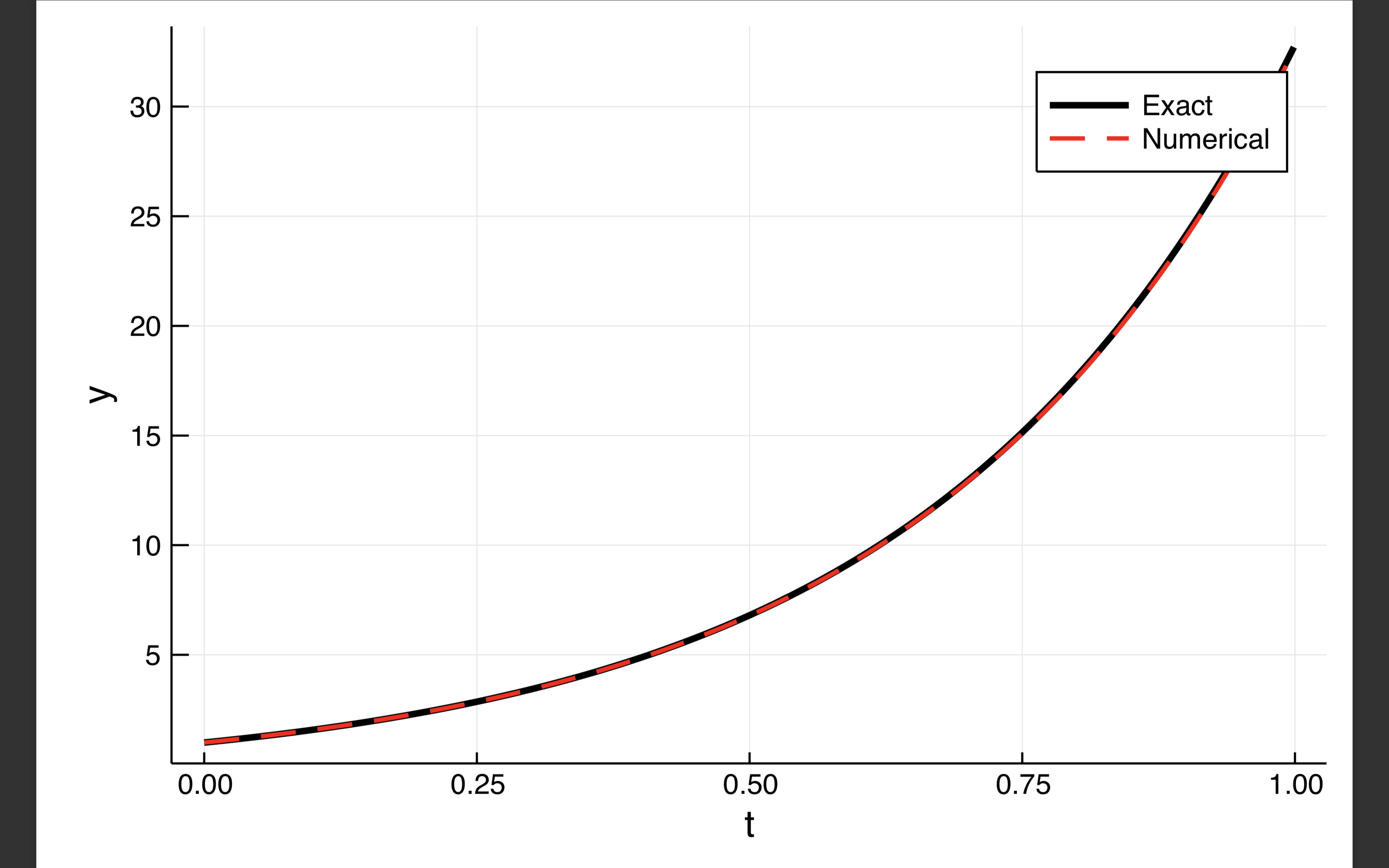
plot(x, f, color=:black, linewidth=3, label="Exact",xlabel="t",ylabel="y" , fmt = :png)
plot!(x, y, color=:red, linewidth=2, linestyle=:dash, label="Numerical" , fmt = :png)
たかだか $t \in [0,1]$だと誤差はなさそう。出力を確認したらpdfで保存しよう(pngだと画質が荒かった)。
savefig("myplot.pdf")
4. 最後に
さて、皆様の環境下でも実行できたでしょうか。やっぱりコードが動くと楽しいですね!
Juliaには微分方程式を解くためのPkgもあるので、そちらで解いたverもこれから書いていこうと思います。
(追記)
書いたよ → こちら