はじめに
カメラと格子模様だけで精度よく変位を計測するサンプリングモアレ法という計測手法を見つけたのでご紹介します。音響計測ではナイキストの定理を満たさなければいけないとよく教わりますが、意図的にエイリアシングさせ、モアレを使うのは面白いなあと思いました。
モアレというのは縞模様と縞模様を重ね合わせたときに見える模様のことです。
参考
以下を参考にしました。
森本吉春,藤垣元治,柾谷明大,"サンプリングモアレ法による変位・ひずみ分布計測",日本真空学会, Vol.54, No.1, PP.32-38, 2011.
新川電機 構造物の形状や変形を調べる格子法・モアレ法 No.1 サンプリングモアレ法による変位分布・ひずみ分布計測
原理
詳細な原理は参考元にわかりやすく書いてありますので、ここでは大雑把な原理を書きます。
やりたいことは、計測対象の歪み(変位)を知ることです。計測対象に縞模様を貼り付けたとします。このときの縞模様の位相と、力が加わり歪んだ縞模様の位相がわかれば、変位に換算することができます。
ある一点の位相を調べる方法を考えます。ここで、振幅を$a$、位相を$\phi$、直流成分を$b$とすると、波は$I = acos\phi + b$と表せます。未知数が3つあるので、測りたい対象に縞模様を少しずらして貼った写真を3枚撮れば位相が求められます。プロジェクタなどで実際に複数の条件の縞模様を投影する方法を格子法と呼びます。
格子法は、複数枚の写真が必要なことから、動画には不向きです。これが1枚の写真から位相が求められれば、手間が減るし動画にも適用できて良さそうです。
変形前と後の縞模様を重ね合わせるとモアレが発生します。これを解析して変位を調べる方法をモアレ法と言いますが、モアレを発生させるために、貼り付けた縞模様とカメラの画素の格子を使う方法がサンプリングモアレ法です。この方法では、1枚の写真から位相のずれた複数のモアレ画像を得ることができます。
サンプリングモアレ法で複数枚のモアレ画像を手に入れる具体的な手順は以下の通りです。
- カメラの画素Nつ分のピッチになる縞模様を計測対象に貼る。
- N画素に1個サンプリングして間引く。
- 元の解像度になるように間引いた画素を線形補間する。
- 間引く画素の始まりをずらして2-3を繰り返すと位相のずれたモアレ画像がN枚手に入る。
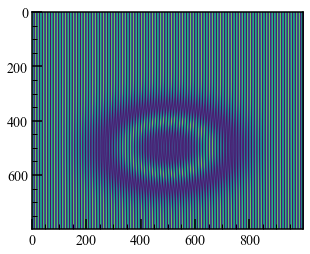
実際にどんな具合か見てみます。ここに縞模様に位相変調を加えた画像を用意しました。中心付近にガウス分布のような変調を加えてあります。見てもあまりわかりません。
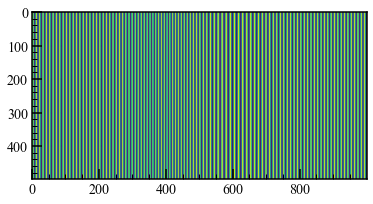
ダウンサンプリングしてモアレを発生させました。
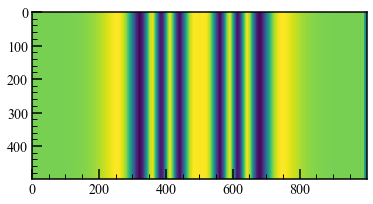
ダウンサンプリングの開始点をずらすと、位相の異なるモアレ画像が手に入ります。
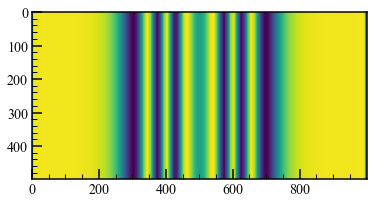
上の画像では10画素で1波長となる縞模様にしました。複数枚のモアレ画像のある一点の輝度をプロットすると以下のようにsin波状になります。これに対してフーリエ変換などをすれば、その点の位相が求まります。
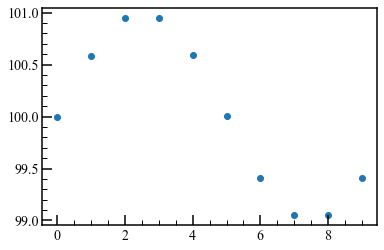
変形前と後の画像に対して同じ操作をして、位相のマップを作ります。その差に縞模様のピッチをかけることで変位が求めます。
試してみる
今回は実際に写真を撮ることはせず、プログラム上のみで試します。
比較のために、位相解析の仲間ということでSPBOS法、解析信号も同じ信号でテストします。
1. 1次元試験信号
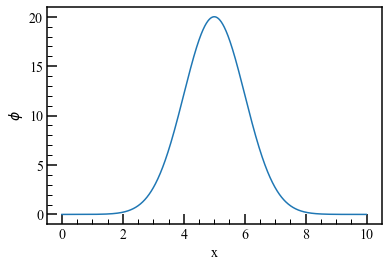
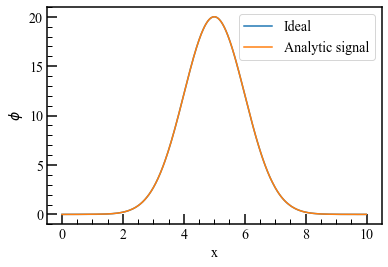
簡単のために1次元の信号で試します。sin波に適当な変調とノイズを加えます。実データでありがちな欠損も加えます。
I = {\displaystyle sin \left( 2\pi \frac{x}{\lambda} + \phi \right) }+b \\
\phi = 20 \exp \left(- \frac{ (x-5)^{ 2 }}{2} \right), b=100
N = 10 #一波長あたりの画素数 4くらいにする
len_x = 10.0 #長さ
dx = 1.0/100.0 #分解能
l_num = len_x/dx
lambda_x = dx * N #波長
x = np.arange(0.0,len_x,dx)
ref_wav = np.sin(2.0*np.pi*x/lambda_x) + np.random.normal(0.0,0.001,len(x))
phi = 20.0*np.exp(-0.5*(x-5.0)**2)
meas_wav = np.sin(2.0*np.pi*x/lambda_x+phi) + np.random.normal(0.0,0.001,len(x))
ref_wav += 100.0
meas_wav += 100.0
ref_wav[300:350] = 0.0
meas_wav[300:350] = 0.0
2. サンプリングモアレ法
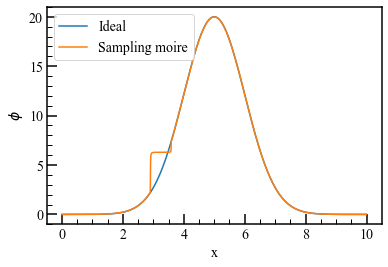
まずはサンプリングモアレ法です。位相の計算はフーリエ変換を使いました。参考文献に則った実装と、numpyのFFTを使った2通り載せておきます。どちらも結果は同じになります。
import numpy as np
from scipy import signal
from scipy import interpolate
def drop_interp1D(array,n,start):
"""
引数array(1次元配列)からn点に1点サンプリングし、もとの配列と同じ要素数となるように間を線形補間する
"""
x = np.linspace(0.0,1.0,array.shape[0])
f = interpolate.interp1d(x[start::n],array[start::n].flatten(),kind="linear",bounds_error=False,fill_value=0.0)
return f(x)
def sampling_moire(array,n):
"""
モアレ画像の位相マップを作成する
"""
sin_sum = np.zeros_like(array,dtype=np.float64)
cos_sum = np.zeros_like(array,dtype=np.float64)
for i in range(n):
ds = drop_interp1D(array,n,i)
sin_sum += ds * np.sin(2.0*np.pi/n*i)
cos_sum += ds * np.cos(2.0*np.pi/n*i)
return np.arctan2(-sin_sum,cos_sum)
def sampling_moire_fft(array,n):
#上の関数のFFT使ったバージョン
ds = []
for i in range(n):
ds.append(drop_interp1D(array,n,i))
fft = np.fft.fft(ds,axis=0)[1] #一番低い周波数成分(直流除く)
return np.angle(fft)
arctanで求まる位相は$- \pi/2$から$\pi/2$なのでnumpyのunwrap関数で繋ぎます。サンプリングモアレ法は位相を計算するところまではある1点のみを使っていますが、このアンラップだけは隣の画素の影響を受けてしまうので、どこかで位相接続に失敗すると全体がダメになっちゃうんですよね。
ここらへんは後で方法を調べる必要がありそうです。今回は適当にnumpy.unwrapを使います。
ref_phase = np.unwrap(sampling_moire(ref_wav,N))
meas_phase = np.unwrap(sampling_moire(meas_wav,N))
diff_phase = meas_phase - ref_phase
3. SPBOS法
この方法は以前、見えないものを見る、家庭でできる流体可視化 BOS法で紹介しました。簡単に手法を説明すると、変形前の縞模様と後の縞模様を引き算して、それに微分をかけ、ローパスフィルタをかけることで位相変調がわかります。
from scipy.ndimage import gaussian_filter
bos = (meas_wav-ref_wav) * np.diff(ref_wav,append=0.0)
bos = gaussian_filter(bos,10.0)
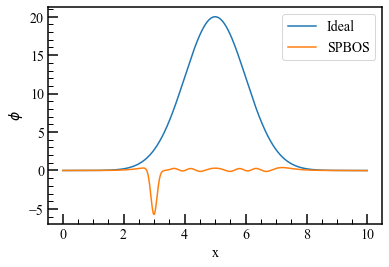
SPBOS法は縞模様の波長に対して変位が微小な場合はうまくいきますが、変位が大きいとダメそうです。
位相変調を1/100にしたらうまくいきました。ただし、SPBOSで得られた値はいい感じに定数倍して合わせにいっています。
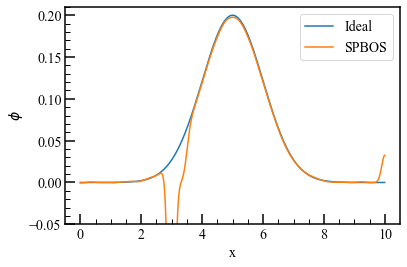
3. 解析信号
最後は音響信号ではよくやる解析信号です。音質評価技術 鈴虫とコオロギの音色の差を検知する変動音解析でも使っています。
解析信号とは、実部に元の信号、虚部に元の信号と位相が90度ずれた信号を持つものです。瞬時周波数や位相、包絡線を出したりできる便利なやつです。
def analytic_signal(wav):
n = len(wav)
fft = np.fft.fft(wav)
fft[n//2:] = 0.0
return np.fft.ifft(2.0*fft)
ref_asig = analytic_signal(ref_wav)
meas_asig = analytic_signal(meas_wav)
asig = np.unwrap(np.angle(meas_asig)-np.angle(ref_asig))
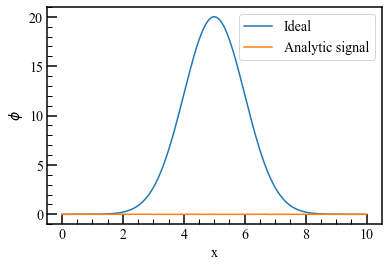
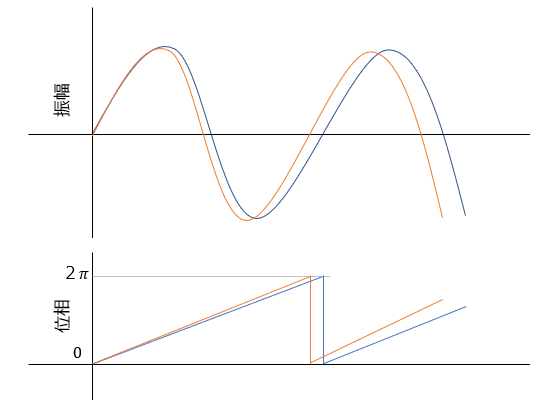
上手くいきません。
まとめ
サンプリングモアレ法について1次元信号で簡単に試してみました。ついでに位相解析の仲間ということで、SPBOS法と解析信号とも比較しました。サンプリングモアレ法は大きな位相変調や欠損でも破綻することなく変位計測ができた一方、SPBOS法は大変形、解析信号は欠損に弱いことがわかりました。
今回は1次元の信号のみを対象としましたが、新しいカメラも買ったので何かしらにパターンを貼り付けて実データでサンプリングモアレ法を試してみたいと思います。