はじめに
透明な気体は肉眼では見えません。それでも見たいときがあります。
そこで役立つのがシュリーレン法やシャドウグラフ法といった流体可視化技術です。
今回は家庭にあるものでこの流体可視化に試みます。
用意するものは基本的にはカメラだけです。
参考文献
こちらを参考に実験しました。
詳細な理論などはこちらを読むことをおすすめします。
BOS法に基づく密度勾配の可視化法の改良
流体可視化技術の紹介
シュリーレン法
夏場に見る陽炎、ライターのガスなど、密度勾配が大きければ肉眼でも何かが見えることがあります。
シャドウグラフ法はこれらが肉眼で見えるのと同じ原理で可視化します。
この手法の感度を更に上げる方法としてシュリーレン法があります。

NOBBY TECH シュリーレン装置
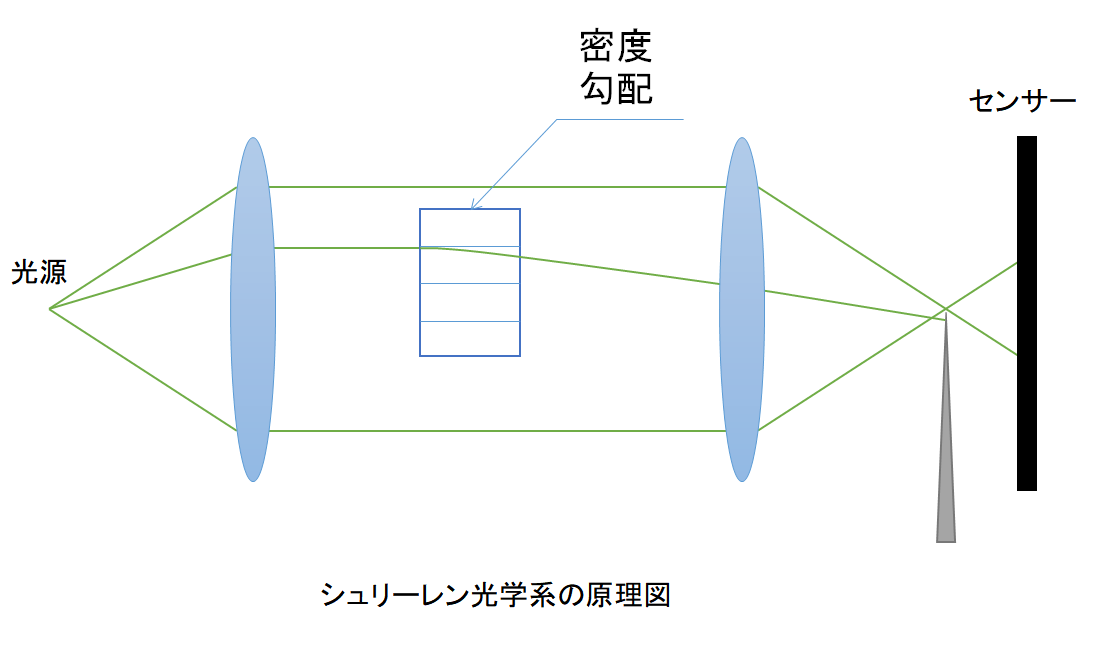
この光学系はこのような構成になっています。
点光源から放たれた光はレンズによって一点に集まります。実際には焦点はある程度の広がりを持っています。この光を半分くらい遮るようにナイフエッジを設置します。
光路上に密度勾配(密度のむら)があると、光は屈折し一点に集まらなくなります。ナイフエッジ側に屈折すれば遮られてセンサー上の像は暗くなり、反対に屈折すれば明るくなります。このようにして密度勾配を明るさの情報として記録することができます。
この方法は感度が高く、綺麗な写真が撮れますが家庭で再現するのは少し大変です。
何が大変かというと、まず準備しなくてはいけないものが多い点です。
- 点光源(ピンホールで遮って点光源を作ります。穴の直径は小さければ小さいほど焦点のスポット径が小さくなり感度が上がります。一方光量も減っていきます。輝度の高い水銀灯のような光源が望ましいです)
- レンズ(平行光である必要ないので最低1個)
- ナイフエッジ
- カメラ
次に光学系の設置の難しさです。光軸を合わせるのに骨が折れます。
特にナイフエッジは正確に焦点の位置にある必要があります。微動ステージがあればいいですが、なければそれなりに工夫が要ります。
SPBOS法(Stripe-patterned Background Oriented Schlieren)
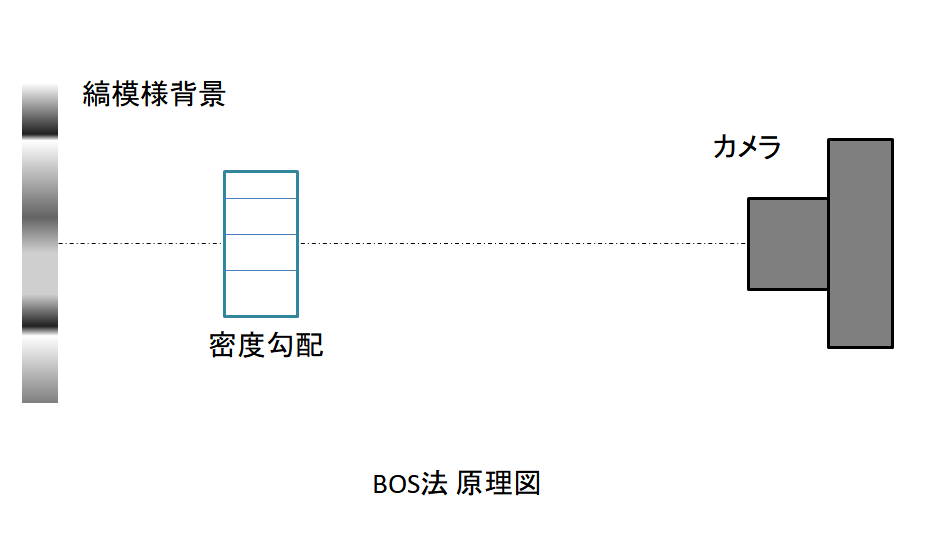
シュリーレン法と同じように密度勾配を可視化できる手法がこのBOS法です。
これにはナイフエッジが要りません。
背景だけの画像と密度勾配のある写真の2枚を撮影し、その差から密度勾配を計算します。
背景にランダムパターンを使用したBOS法もありますが、そちらはPIVのように相互相関を計算してずれを求めるのでプログラムが面倒になります。
今回はプログラムも簡単になる縞模様を利用したSPBOS法でやります。
実験
準備するもの
- 縞模様のスクリーン
- カメラ
- 測りたいもの
今回使用したものは以下の通りです。
- iphone8
- D5100, AF-S DX NIKKOR 55-300mm f/4.5-5.6G ED VR
- モノタロウのエアダスター
スクリーンはスマホでもプリンターで紙に印刷しても良いと思います。
カメラはRAWで保存できるものが望ましいです。
D5100のビット深度は14bit(16383階調)ありますが、jpgで保存するとディスプレイの階調に合わせて8bit(255階調)しかありません。
それとガンマ補正が効いているので、リニアに戻すと更に悪くなります。
三脚もあれば良いですが、床に置くのでも良いと思います。シャッターを押すときはカメラがぶれないように気をつけます。
撮影
今回はこのように設置しました。焦点距離300mm、露光時間1/60、F値20、ISO感度400です。
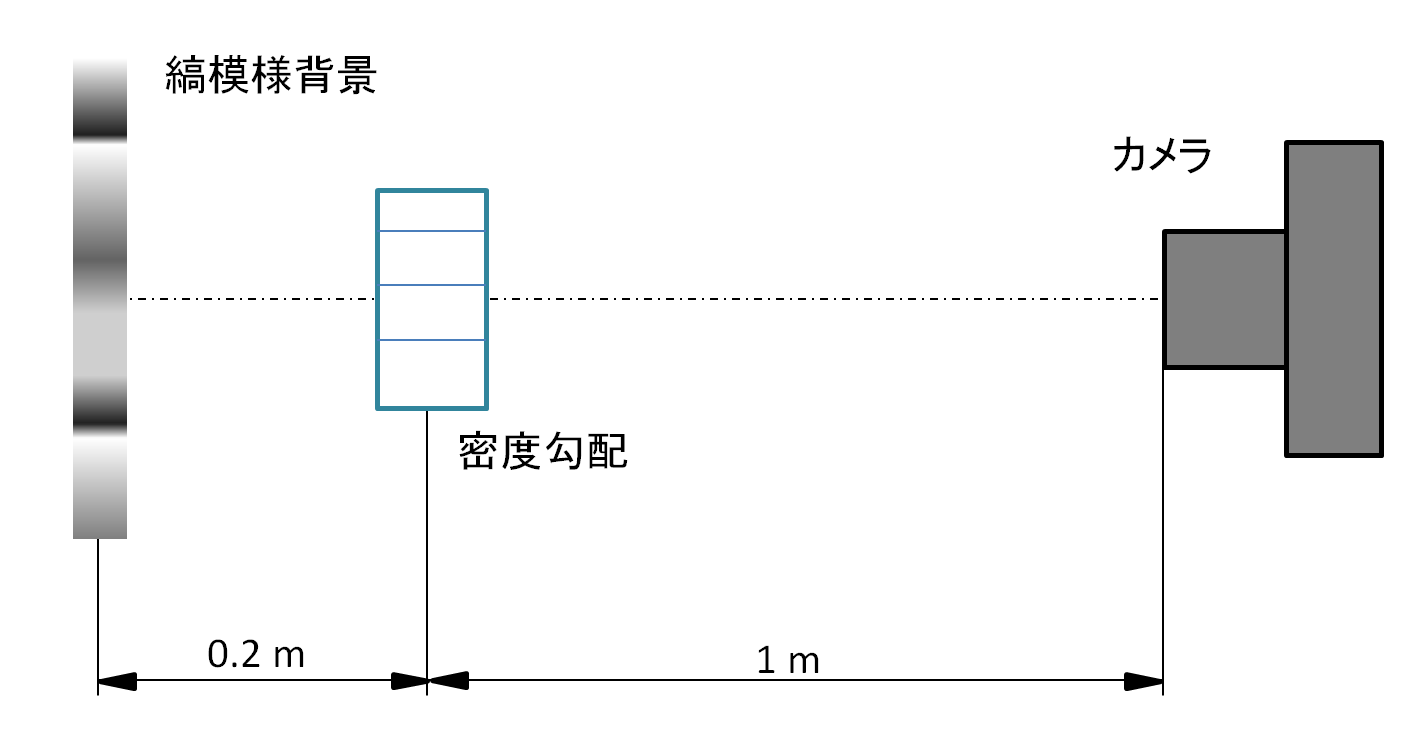
カメラのピントはスクリーンに合わせます。
スクリーンと測定物の距離に気をつける必要があります。
近すぎると感度がでません。
仮に、スクリーンのすぐ近くに密度勾配があって光が曲がったとしても、その曲がった光は曲がらなかったときと同じ位置に結像してしまいます。
反対に遠すぎると測定物がボケます。F値を上げて被写界深度を深くして対応します。
背景用の画像は以下のプログラムで作成しました。
import numpy as np
# ディスプレイ
ppi = 326 # 1inch(25.4mm)あたりのピクセル数
x_pix = 750 # 横解像度
y_pix = 1334 #縦解像度
pix_per_mm = ppi / 25.4
x_mm = x_pix / pix_per_mm
y_mm = y_pix / pix_per_mm
lam = 1.0 # mm
def sin_img(direction="x",bit=8):
if direction == "x":
x = np.linspace(0.0,x_mm,x_pix)
sin = np.sin(2.0*np.pi*x/lam)
img = np.tile(sin,(y_pix,1)).T
img = 0.5 * (img + 1.0) * (2**bit-1.0)
elif direction == "y":
y = np.linspace(0.0,y_mm,y_pix)
sin = np.sin(2.0*np.pi*y/lam)
img = np.tile(sin,(x_pix,1))
img = 0.5 * (img + 1.0) * (2**bit-1.0)
if bit == 8:
img = img.astype(np.uint8)
elif bit == 16:
img = img.astype(np.uint16)
else:
print("bit数は8か16")
return img
解析
まずは解析に使用したプログラムを貼ります。
RAW画像はrawpyを使用して現像します。ガンマ補正のないリニアスケールの輝度値を使用します。
import rawpy
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import cv2
from pathlib import Path
def postproccesing(path):
raw = rawpy.imread(str(path))
return raw.postprocess(gamma=[1.0,1.0],
no_auto_bright=True,
output_color=rawpy.ColorSpace.raw,
use_camera_wb=True,
use_auto_wb=False,
output_bps=16,
no_auto_scale=True
)
ref_path = Path("data/ref2.NEF")
jet_path = Path("data/jet2.NEF")
ref_img = postproccesing(ref_path)
jet_img = postproccesing(jet_path)
ref_gray = ref_img[:,:,1] #グレイスケール
jet_gray = jet_img[:,:,1]
可視化は差分を取り、空間の微分をかけるだけです。
差分を取ることで密度勾配によって屈折した部分がわかります。
同じ方向に光が曲がったにしても、背景の模様によって暗くなる側か明るくなる側になるため、勾配を掛け算する必要があります。
bos = (jet_gray-ref_gray) * np.gradient(0.5*(jet_gray+ref_gray))[1]
ローパスフィルタをかけます。
適当に見た目を見ながら帯域を決めます。
def fft_lpf(img,r):
#周波数空間マスク
mask = np.zeros_like(img)
X,Y = np.meshgrid(np.arange(img.shape[1])-img.shape[1]/2.0,np.arange(img.shape[0])-img.shape[0]/2.0)
mask[np.sqrt(X**2 + Y**2) < r] = 1.0
#FFT
fft_img = np.fft.fftshift(np.fft.fft2(img))
fft_img *= mask
return np.abs(np.ifft.fft2(np.fft.fftshift(fft_img)))
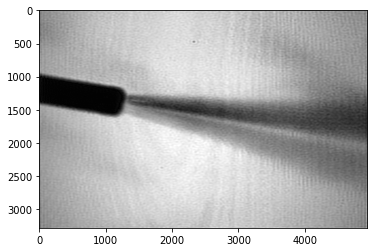
ノイズが多いですが、しっかりジェットが可視化できています。
もう少し工夫すればノイズは減らせそうです。
2020/04/14 追記
ちゃんとカメラ固定して撮影し直し、明るさを後から調整してノイズを減らしました。
このくらいきれいに撮れます。
まとめ
家庭にあるものだけで、それなりに流体可視化ができることを示しました。
ぜひ試してみてください。