対象
数値計算を使って勉強している物理,化学系の学生向け
はじめに
物理現象を記述する微分方程式を数値的に解く,みたいなのは理系専攻のカリキュラムなら,どこもやっていると思います.
とりあえず差分化してコードに直せば,解を出してくれて,グラフに直せばそのイメージが掴める,とても便利な方法です.
一方で面倒なこともあります.
一つがコードを書く手間です.
数値計算の講義ではCが主流かと思いますが,C言語は手軽に扱うには向きません.デバッグに時間もかかります.
また,刻み幅の調整も問題です.この値が大きすぎると正しい解が得られません,かといって,小さすぎると計算時間がかかりすぎます.
この二つの面倒さに対し,自分なりに解決を行いましたので,紹介することにしました
pythonとscipy.integrate.solve_ivp
まず,言語としてPythonを採用します.pythonといえば遅い言語のイメージがありますが,数値計算ライブラリの拡充により,ちょっとした計算をやるときには個人的にほぼ一択です.まあ3次元シミュレーションとかになるときついんですが.
そして,pythonのscipy.integrateライブラリからsolve_ivpを用います.solve_ivpは,(下は公式の解説),刻み幅の自動調節を行ってくれる手法をwrapした(連立)常微分方程式solverです.
solve_ivpを用いてコードを書き,微分方程式を解いていきたいと思います.
物理的にも面白そうな例をたくさん用意しました.
scipy.integrate.solve_ivpと,計算結果も気に入っていただけると幸いです.
目次
簡単なODE
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
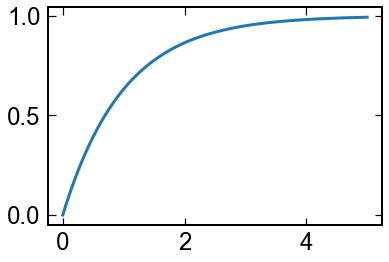
単一緩和の減衰挙動
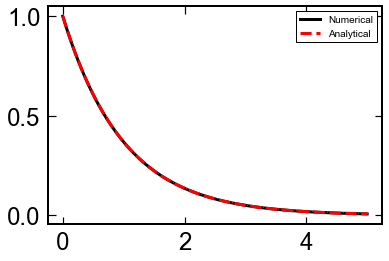
まず, 単一緩和の減衰運動を解いてみましょう.
$$
\frac{{\rm d}x}{{\rm d}t} = -x
$$
init = [1.0]
t_span = [0.0,5.0]
t_eval = np.linspace(*t_span,100) # time for sampling
def decay(t,x): return -x
sol = solve_ivp(decay,t_span,init,method='RK45',t_eval=t_eval)
solve_ivpでラップされたRK45法により,内部で精度を保証できるよう時間刻みを勝手に調整してくれます.嬉しいですね!
plt.plot(sol.t,sol.y[0,:],'k,-')
plt.plot(sol.t,np.exp(-sol.t),'r,--')
plt.legend(['Numerical','Analytical'])
plt.show()
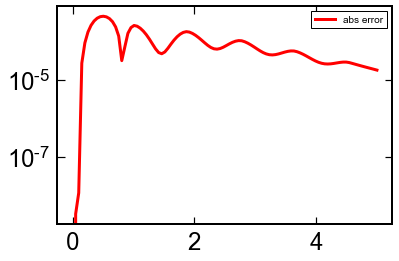
plt.semilogy(sol.t,np.abs(sol.y[0,:]-np.exp(-sol.t)),'r')
plt.legend(['abs error'])
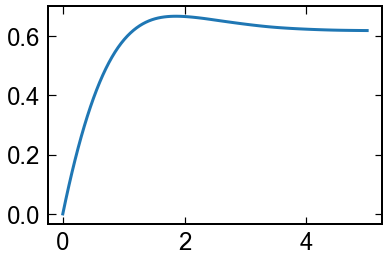
1次元調和振動子
次に,1次元調和振動子を例に挙げます.
ハミルトニアンを書き下します.
$$
H = \frac{p^2}{2} + \frac{q^2}{2}
$$
簡単のため定数は1としました. 正準方程式から連立ODEを得ます.
$$
\dot p = -q\
\dot q = p
$$
勿論,連立ODEも簡単に扱うことができます.
p0 = 1.0; q0 = 0.0
init = [p0,q0]
t_span = [0.0,20.0]
t_eval = np.linspace(*t_span,100) # time for sampling
def halmonic(t,x):
p,q = x
return [-q,p]
sol = solve_ivp(halmonic,t_span,init,method='RK45',t_eval=t_eval)
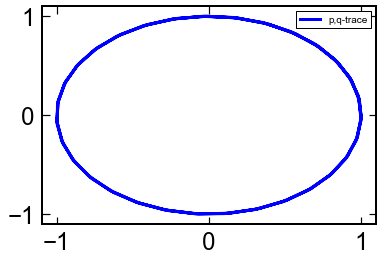
plt.plot(sol.y[0,:],sol.y[1,:],'b,-')
plt.legend(['p,q-trace'])
plt.show()
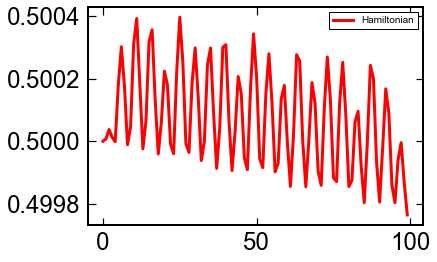
plt.plot(sol.y[0,:]**2/2+sol.y[1,:]**2/2,'r,-')
plt.legend(['Hamiltonian'])
plt.show()
非線形ODE
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from mpl_toolkits.mplot3d import Axes3D
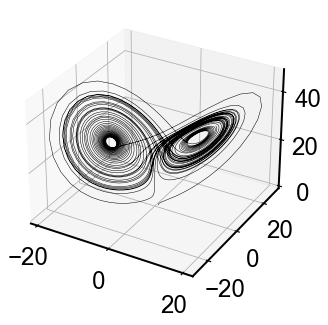
ローレンツアトラクタ
次はローレンツアトラクタを描いてみましょう.
$$
\frac{{\rm d}x}{{\rm d}t} = -px +py ,
\frac{{\rm d}y}{{\rm d}t} = -xz +rx -y ,
\frac{{\rm d}z}{{\rm d}t} = -xy +bz
$$
ここで,$p=10, r=28, b=8/3$を使いました(wikipedia). パラメーターは引数argに追加することができます.
init = [1.0,0.0,0.0]
t_span = [0.0,50.0]
t_eval = np.linspace(*t_span,3000) # time for sampling
p=10.; r=28.; b=8./3.;
def lorenz(t,X,p,r,b):
x,y,z = X
return [-p*x+p*y, -x*z+r*x-y, x*y-b*z]
sol = solve_ivp(lorenz,t_span,init,method='RK45',t_eval=t_eval,args=(p,r,b,))
綺麗なカオス的ふるまいが見れます.
7/2追記)
許容誤差を調整しないと誤差が大きくなってしまうみたいですね.詳しくはこちらの記事を.
https://qiita.com/Sunset_Yuhi/items/d938718ad277eeab746c
fig = plt.figure(); ax = Axes3D(fig)
ax.plot(sol.y[0,:],sol.y[1,:],sol.y[2,:],'k-',lw=0.5)
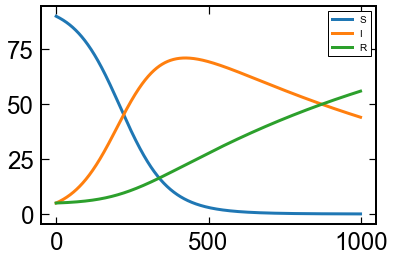
SIRモデル
Sが感染しうる個体,Iが感染者,Rが免疫,死亡,位置的などの意味での抵抗獲得者を表します.
$$
\begin{eqnarray}
\frac{{\rm d}S}{{\rm d}t}&&=-\frac{\beta IS}{N}\
\frac{{\rm d}I}{{\rm d}t}&&=+\frac{\beta IS}{N}-\gamma I\
\frac{{\rm d}R}{{\rm d}t}&&=\gamma I\
\end{eqnarray}
$$
N = 100
init = [N*0.9,N*0.05,N*0.05]
t_span = [0.0,10.0]
t_eval = np.linspace(*t_span,1000) # time for sampling
β = 1.5; γ = 0.1;
def lorenz(t,SIR,N,β,γ):
S,I,R = SIR
return [-β*I*S/N, +β*I*S/N-γ*I, γ*I]
sol = solve_ivp(lorenz,t_span,init,method='RK45',t_eval=t_eval,args=(N,β,γ,))
基本再生産数$\beta/\gamma$を15にしています.
結構な感染爆発が起きるが,中々治らない.という感じになります.
S,I,R = sol.y
plt.plot(S)
plt.plot(I)
plt.plot(R)
plt.legend(['S','I','R'])
テンソルODE
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
Maxwellの応力挙動
連続体を扱うとき,2階のテンソルが頻出します.
例えばMaxwell流体の3次元構成関係を見てましょう,応力$\sigma_{ij}$の時間発展は,$\kappa_{ij}=\nabla_i v_j$は速度勾配,$G$は平衡圧として,以下の形で書けます.
$$
\frac{{\rm d}\boldsymbol\sigma}{{\rm d} t} =
\boldsymbol\kappa\cdot\boldsymbol\sigma +
\boldsymbol\sigma\cdot\boldsymbol\kappa^T - (\boldsymbol \sigma-G\boldsymbol I)
$$
$ij$成分を陽に考えて実装するのは煩わしいですね.
でもnumpyを使えば右辺の計算を見た目そのままにコードに書くことができます.
solve_ivpに解いてもらいましょう.$xy$方向にせん断変形を与えます.
dim = 3
σ = np.eye(dim)
κ = np.zeros_like(σ)
δ = np.eye(dim)
κ[0,1] = 1.0 # xy-shear
init = σ.flatten()
t_span = [0.0,5.0]
t_eval = np.linspace(*t_span,100) # time for sampling
def maxwell(t,σ,κ):
σ = σ.reshape(dim,dim)
dσ = κ.dot(σ) + σ.dot(κ.T) - (σ - δ)
return dσ.flatten()
sol = solve_ivp(maxwell,t_span,init,method='RK45',t_eval=t_eval,args=(κ,))
maxwell関数内で,受け取った$\sigma$を二次元にreshapeすること, 返り値を一次元で返す必要があることに注意します.
ギリシャ文字はjupyter labで打っています. 読むときに楽で良いですね.
成長せん断粘度$\eta_s = \sigma_{xy}/\kappa_{xy}$を見てましょう.
plt.plot(sol.t,sol.y[1]/κ[0,1])
Giesekusの応力挙動
Giesekus流体に変更してみましょう. 構成式は以下の形をしており.
$$
\frac{{\rm d}\boldsymbol\sigma}{{\rm d} t} =
\boldsymbol\kappa\cdot\boldsymbol\sigma +
\boldsymbol\sigma\cdot\boldsymbol\kappa^T - (\boldsymbol \sigma-G\boldsymbol I) -
\alpha(\boldsymbol\sigma - G\boldsymbol I)\cdot (\frac{\boldsymbol\sigma}{G} - \boldsymbol I)
$$
パラメータ$\alpha\in(0,1]$に依存する非線型項を持ちます.
dim = 3
σ = np.eye(dim)
κ = np.zeros_like(σ)
δ = np.eye(dim)
α = 0.5
κ[0,1] = 1.0 # xy-shear
init = σ.flatten()
t_span = [0.0,5.0]
t_eval = np.linspace(*t_span,100) # time for sampling
def giesekus(t,σ,κ,α):
σ = σ.reshape(dim,dim)
dσ = κ.dot(σ) + σ.dot(κ.T) - (σ - δ) - α * (σ - δ).dot(σ - δ)
return dσ.flatten()
sol = solve_ivp(giesekus,t_span,init,method='RK45',t_eval=t_eval,args=(κ,α))
粘度のオーバーシュートと定常値の低減(シアシニング)を観察できます.
plt.plot(sol.t,sol.y[1]/κ[0,1])
1次元場PDE (基礎編)
時間だけでなく位置$x$に依存する偏微分方程式を考えてみましょう. $x$に対する空間の差分化さえできれば.後は連立ODEと同じになります.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
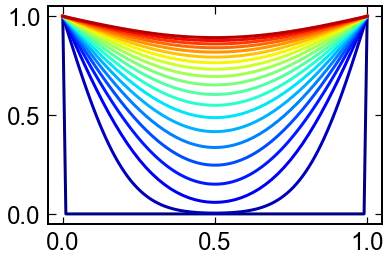
拡散方程式
熱拡散の問題を考えます.
一次元場の熱保存式は,次の形で書けます
$$
\frac{\partial \theta}{\partial t}= \alpha\frac{\partial^2 \theta}{\partial x^2}
$$
$x$の空間差分をとると.
$$
\frac{\partial \theta^n}{\partial t}= \alpha\frac{\theta^{n+1}-2\theta^{n}+\theta^{n-1}}{\Delta x^2}
$$
$\theta=1$ at $x=0,1$を境界として,$x$が$[0,1]$の範囲を計算します.
nx = 100
x = np.linspace(0.0,1.0,nx)
θ = np.zeros_like(x)
θ[0] = θ[-1] = 1.
Δx = 1.0/(nx-1)
α = 0.25
init = θ
t_span = [0,1]
t_eval = np.linspace(*t_span,20) # time for sampling
def diffusion(t,θ,α,Δx):
dθ = α * np.diff(θ,2)/(Δx**2)
return np.hstack([0.0,dθ,0.0])
sol = solve_ivp(diffusion,t_span,init,method="RK45",t_eval=t_eval,args=(α,Δx))
cmap = plt.get_cmap('jet')
Np = len(sol.t)
for i in range(Np):
plt.plot(x,sol.y[:,i],c=cmap(i/Np))
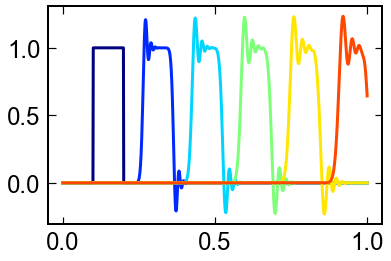
移流方程式
矩形波の進行問題を考えてみましょう.
等速流一次元場の質量保存式は,次の形で書けます.
$$
\frac{\partial \rho}{\partial t}+ v_x\frac{\partial \rho}{\partial x}=0
$$
この差分の取り扱いは結構難しいです.ここでは$x$の2次後進差分をとり,許容相対誤差(rtol)を小さくしてみます.
$$
\frac{\partial \rho^n}{\partial t}= -v_x\frac{3\rho^{n}-4\rho^{n-1}+\rho^{n-2}}{2\Delta x}
$$
$v_x=1$を一定値として,$x$が$[0,1]$の範囲を考えます.初期条件は,$\rho(0.1<x<0.2)=1$ これ以外で$0$とします.
nx = 1000
vx = 0.8
x = np.linspace(0.0,1.0,nx)
ρ = np.where((0.1<x)&(x<0.2),1.0,0.0)
Δx = 1.0/(nx-1)
init = ρ
t_span = [0,1]
t_eval = np.linspace(*t_span,6) # time for sampling
def advection(t,ρ,vx,Δx):
dρ = -vx * np.convolve(ρ,[3.0,-4.0,1.0],'valid')/(2*Δx)
return np.hstack([0.0,0.0,dρ])
sol = solve_ivp(advection,t_span,init,method="RK45",t_eval=t_eval,args=(vx,Δx),rtol=1e-5)
少し乱れているが,進行する様子が観察できます.ちなみに前進差分で計算すると簡単に発散し,大変なことになります(なった).
cmap = plt.get_cmap('jet')
Np = len(sol.t)
for i in range(Np):
plt.plot(x,sol.y[:,i],c=cmap(i/Np))
波動方程式
時間方向の二階微分式中に登場する波動方程式を考えます.
$$
\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}
$$
ここで,ある$x$における$u=u^n$について$u, u'=\frac{\partial u}{\partial t}$に対する2本のODEが書けます
$$
\begin{eqnarray}
\frac{\partial u }{\partial t}&&= u'\
\frac{\partial u'}{\partial t}&&= c^2\frac{u^{n+1}-2u+u^{n-1}}{\Delta x^2}
\end{eqnarray}
$$
正弦波形の時間発展を見てみましょう.
nx = 100
x = np.linspace(0.0,1.0,nx)
u = np.sin(2.0*np.pi*x)
du = np.cos(3.0*np.pi*x)
Δx = 1.0/(nx-1)
c2 = 0.05
init = np.hstack([u,du])
t_span = [0,1]
t_eval = np.linspace(*t_span,50) # time for sampling
def wave(t,U,c2,Δx):
u,du = U[:nx],U[nx:]
u[0] = u[-1] = 0.0
ddu = c2 * np.diff(du,2)/(Δx**2)
return np.hstack([du,0.0,ddu,0.0])
sol = solve_ivp(wave,t_span,init,method="RK45",t_eval=t_eval,args=(c2,Δx))
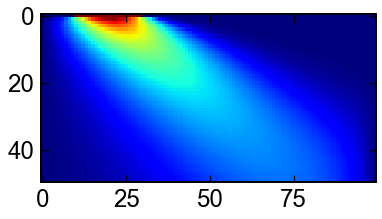
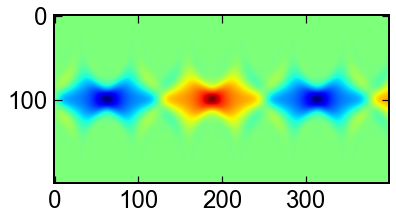
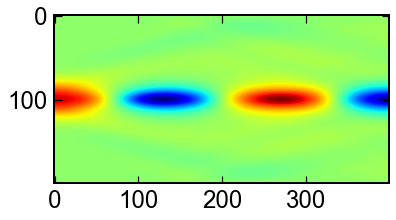
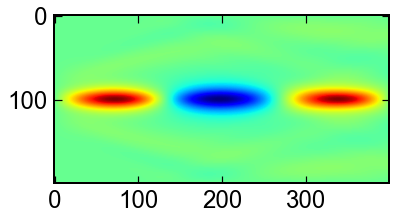
u[0..n-1],du[0..n-1]をまとめて扱うのがコツです.
上の画像は$u$,下の画像は$u'$の時間発展を表しています.
fig,ax = plt.subplots()
ax.imshow(sol.y.T[:,:nx],cmap='jet')
fig,ax = plt.subplots()
ax.imshow(sol.y.T[:,nx:],cmap='jet')
1次元場PDE (応用編)
Burgers方程式
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
ナビエストークス方程式の移流項$u\partial_x u$と粘性項$\partial_{xx} u$のみを考える形です.
$$
\partial_t u + \lambda_1 u\partial_x u = \lambda_2 \partial_{xx} u
$$
移流拡散方程式とも呼ばれています.
# parameters
nx = 100
Δx = 1.0/(nx-1)
λ1 = 1.0; λ2 = 0.1;
# init
x = np.linspace(0.0,1.0,nx)
u = np.zeros_like(x)
u[10:30] = 1.0
init = u
# time
t_span = [0.,0.5]
t_eval = np.linspace(*t_span,50) # time for sampling
# ODEs
def ODEs(t,u,λ1,λ2,Δx):
du = - λ1 * (np.diff(u)/(Δx))[1:] + λ2 * np.diff(u,2)/(Δx**2)
return np.hstack([0.0,du,0.0])
# solve
sol = solve_ivp(ODEs,t_span,init,method="RK45",t_eval=t_eval,args=(λ1,λ2,Δx))
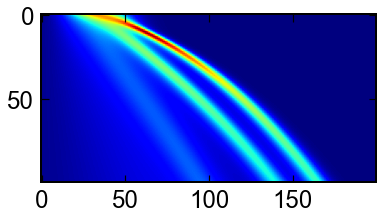
進行しながら滑らかになる様子が見れる.
fig,ax = plt.subplots()
ax.imshow(sol.y.T,cmap='jet')
KdV方程式
コルトヴェーグと,ド・フリースにより定式化された.非線形波を表す方程式です.
$$
\partial_t u + 6u \partial_x u + \partial_{xxx}u=0
$$
パラメータは,この論文を参考にさせていただきました.
http://advances.sciencemag.org/content/3/4/e1602614
# parameters
nx = 200
Δx = 60./(nx-1)
# init
x = np.linspace(0.0,60.0,nx)
u = np.exp(-((x-10.0)/(5.0))**2)
init = u
# time
t_span = [0.,20.0]
t_eval = np.linspace(*t_span,100) # time for sampling
# ODEs
def ODEs(t,u,Δx):
du = - 6 * u[2:-2] * np.convolve(u,[1.,0.,-1.],'valid')[1:-1]/(2*Δx) - np.diff(u,3)[1:]/(Δx**3)
return np.hstack([0.,0.,du,0.,0.])
# solve
sol = solve_ivp(ODEs,t_span,init,method="RK45",t_eval=t_eval,args=(Δx,),rtol=1e-8)
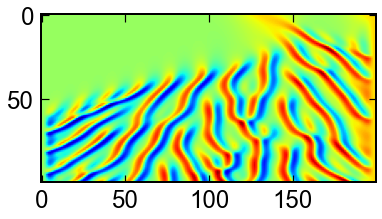
正規分布の初期速度を置いた.時間の進行とともに幾つかの孤立波になっています.
fig,ax = plt.subplots()
ax.imshow(sol.y.T,cmap='jet')
KS方程式
蔵元ーシバシンスキー方程式.火砕流の挙動を表すよう定式化されました.4階微分が特徴的.拡散の強さが拡散します.
$$
\partial_t u + u\partial_x u + \partial_{xx} u + \partial_{xxxx} u = 0
$$
# parameters
nx = 200
Δx = 100./(nx-1)
# init
x = np.linspace(0.0,60.0,nx)
u = np.exp(-((x-40.0)/(5.0))**2) + np.exp(-((x-60.0)/(5.0))**2)
init = u
# time
t_span = [0.,100.0]
t_eval = np.linspace(*t_span,100) # time for sampling
# ODEs
def ODEs(t,u,Δx):
du = - u[2:-2] * np.convolve(u,[1.,0.,-1.],'valid')[1:-1]/(2*Δx)\
- np.diff(u,2)[1:-1]/(Δx**2)\
- np.diff(u,4) /(Δx**4)
return np.hstack([0.,0.,du,0.,0.])
# solve
sol = solve_ivp(ODEs,t_span,init,method="RK45",t_eval=t_eval,args=(Δx,),rtol=1e-8)
インパクトあって目に楽しい図ができます
fig,ax = plt.subplots()
ax.imshow(sol.y.T,cmap='jet')
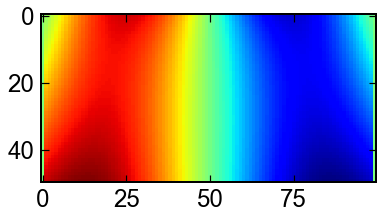
Schorodinger方程式
理系大学生の関門として名高いシュレディンガー方程式.数値計算を通してイメージを掴んでみましょう.
一次元では,定数を1,二次関数型のポテンシャル場$V(x)=x^2/2$を考えると以下の形で書けます.
$$
i\partial_t \Psi = -\left(\frac{1}{2}\partial_{xx}- \frac{x^2}{2}\right)\Psi
$$
ちなみにsolve_ivpはcomplexもrealと変わらず扱えます.すごい!
# parameters
nx = 200
Δx = 15./(nx-1)
# init
x = np.linspace(-7.5,7.5,nx)
Ψ = 2.*np.exp(-x**2) + 0.j
init = Ψ
# time
t_span = [0.,20.0]
t_eval = np.linspace(*t_span,400) # time for sampling
# ODEs
def ODEs(t,Ψ,Δx):
dΨ = -1.j*(- 0.5*np.diff(Ψ,2)/(Δx**2) + 0.5*(x**2*Ψ)[1:-1])
return np.hstack([0.+0.j,dΨ,0.+0.j])
# solve
sol = solve_ivp(ODEs,t_span,init,method="RK45",t_eval=t_eval,args=(Δx,),rtol=1e-8)
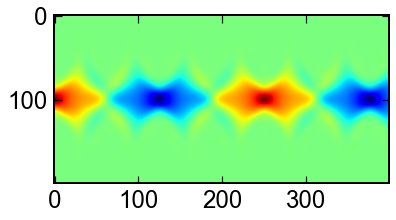
ポテンシャルによって電子波が中心にトラップされています.
fig,ax = plt.subplots()
ax.imshow(sol.y[:].real,cmap='jet')
fig,ax = plt.subplots()
ax.imshow(sol.y[:].imag,cmap='jet')
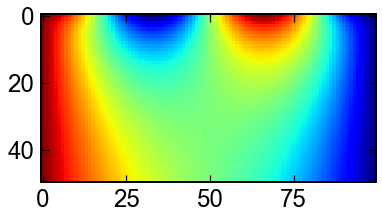
Non-linear Schirodinger方程式
ポテンシャル関数が$V(x)=|\Psi|^2$(引力)のときも有名です.
$$
i\partial_t \Psi = -\left(\frac{1}{2}\partial_{xx}+ |\Psi|^2\right)\Psi
$$
# parameters
nx = 200
Δx = 10./(nx-1)
# init
x = np.linspace(-5.0,5.0,nx)
Ψ = 2.*np.exp(-x**2) + 0.j
init = Ψ
# time
t_span = [0.,np.pi]
t_eval = np.linspace(*t_span,400) # time for sampling
# ODEs
def ODEs(t,Ψ,Δx):
dΨ = -1.j*(- 0.5*np.diff(Ψ,2)/(Δx**2) - (np.abs(Ψ)**2*Ψ)[1:-1])
return np.hstack([0.+0.j,dΨ,0.+0.j])
# solve
sol = solve_ivp(ODEs,t_span,init,method="RK45",t_eval=t_eval,args=(Δx,),rtol=1e-8)
fig,ax = plt.subplots()
ax.imshow(sol.y[:].real,cmap='jet')
fig,ax = plt.subplots()
ax.imshow(sol.y[:].imag,cmap='jet')
2次元場PDE (基礎編)
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
from scipy.signal import convolve2d
from scipy.integrate import solve_ivp
from mpl_toolkits.mplot3d import Axes3D
拡散方程式
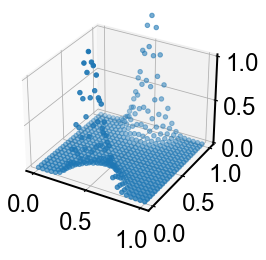
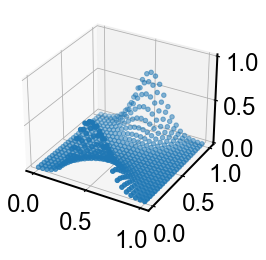
温度場の二次元拡散方程式を計算してみましょう.
$$
\partial_t \theta = k(\partial_{xx}+\partial_{yy}) \theta
$$
ラプラシアンを計算する時scipy.convolve2dが便利です."fill"オプション指定で0境界,"wrap"で周期境界,"symm"で勾配なし境界条件が作れます
# parameter
N = Nx = Ny = 25
Δ = Δx = Δy = 1./(N-1)
k = 0.01
D = (k/Δ**2)
A = np.array([[0.0, D,0.0],
[D ,-4*D, D],
[0.0, D,0.0],])
# init
x = np.linspace(0.0,1.0,N)
θ = np.zeros((N,N))
θ[0,N//2] = 50
t_span=[0.0,1.0]
t_eval=np.linspace(*t_span,3)
# ODEs
def ODEs(t,θ):
θ = θ.reshape(N,N)
dθ = convolve2d(θ,A,'same','wrap')
return dθ.flatten()
#
sol = solve_ivp(ODEs,t_span,θ.reshape(-1),'RK45',t_eval)
x = np.linspace(0.0,1.0,N)
x,y = np.meshgrid(x,x)
for θ in sol.y.T:
θ = θ.reshape(N,N)
fig,ax = plt.subplots(subplot_kw=dict(projection='3d',zlim=(0.0,1.0)))
ax.scatter(x,y,θ)
plt.show()
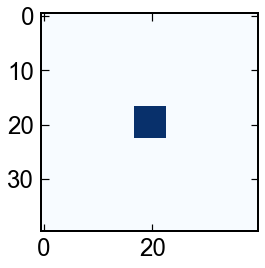
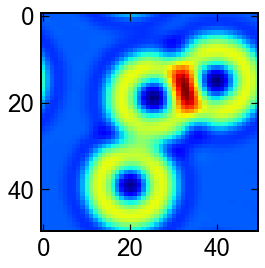
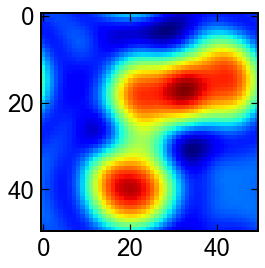
Gray-Scott モデル
反応拡散方程式のインスタンスの一つです.
$$
\partial_t u = D_u (\partial_{xx}+\partial_{yy})u + f(u,v) \
\partial_t v = D_v (\partial_{xx}+\partial_{yy})u + g(u,v)
$$
のうち,関数$f,g$を
$$
f(u,v) = - uv^2 + F(1-u) \
g(u,v) = + uv^2 - v(F+k)
$$
と与えたもの.
説明は例えば,こちらの記事をどうぞ.
https://qiita.com/kaityo256/items/3c07252ab63591256835
コード中のパラメータも参考にさせていただきました.
# parameter
N = Nx = Ny = 40
Δ = Δx = Δy = 1.0
Du = (0.1 /Δ**2)
Dv = (0.05/Δ**2)
F = 0.04
k = 0.06075
A = np.array([[0.0 , Du, 0.0],
[Du ,-4*Du, Du],
[0.0 , Du, 0.0],])
B = np.array([[0.0 , Dv, 0.0],
[Dv ,-4*Dv, Dv],
[0.0 , Dv, 0.0],])
# init
x = np.linspace(0.0,1.0,N)
u = np.zeros((N,N))
v = np.zeros((N,N))
init = ()
h = N//2
u[h-3:h+3, h-3:h+3] = 0.9
v[h-1:h+1, h-1:h+1] = 0.7
t_span=[0.0,3000.0]
t_eval=np.linspace(*t_span,4)
# ODEs
def ODEs(t,U):
u,v = U[:N*N].reshape(N,N),U[N*N:].reshape(N,N)
du = convolve2d(u,A,'same','wrap') - u*v**2 + F*(1.0-u)
dv = convolve2d(v,B,'same','wrap') + u*v**2 - v*(F + k)
return np.hstack([du.flatten(),dv.flatten()])
#
sol = solve_ivp(ODEs,t_span,np.hstack([u.flatten(),v.flatten()]),'RK45',t_eval,rtol=1e-5)
とても面白い模様が見れます. 他の例としてはFitzHugh–Nagumo方程式なども有名みたいです.
for u in sol.y.T[:,:N*N]:
u = u.reshape(N,N)
fig,ax = plt.subplots(figsize=(4,4))
ax.imshow(u,cmap='Blues')
plt.show()
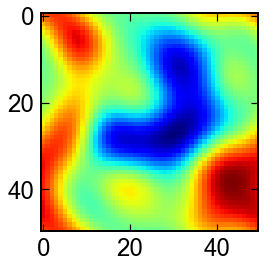
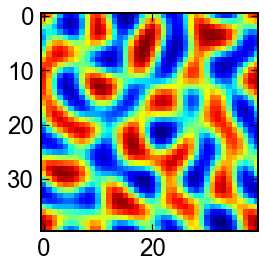
BZ反応
平衡点周りを振動しつつ,ゆっくりと平衡状態に近づく反応です.
モデルはいくつかあるみたいですが,今回は下の参考文献中のモデルを用いました.
$$
\epsilon \partial_t x = x(1-x) -fz\frac{x-q}{x+q}+D_x (\partial_{xx}+\partial_{yy})x \
\partial_t z = x-z + D_z (\partial_{xx}+\partial_{yy}) z
$$
これは,
https://cattech-lab.com/science-tools/bz-reaction/
を参考にさせていただきました.
# parameter
N = Nx = Ny = 50
Δ = Δx = Δy = 2.0/(N-1)
Dx = (1.0e-5/Δ**2)
Dz = (1.0e-5/Δ**2)
f = 0.95
ϵ = 0.08
q = 0.075
A = np.array([[0.0 , Dx, 0.0],
[Dx ,-4*Dx, Dx],
[0.0 , Dx, 0.0],])
B = np.array([[0.0 , Dz, 0.0],
[Dz ,-4*Dz, Dz],
[0.0 , Dz, 0.0],])
# init
x = 0.1*np.ones((N,N))
z = 0.1*np.ones((N,N))
z[N//2-6,N//2] *= 1.01
z[N//2-10,N//2+15] *= 1.01
z[N//2+14,N//2-5] *= 1.01
t_span=[0.0,500.0]
t_eval=np.linspace(*t_span,5)
# ODEs
def ODEs(t,X):
x,z = X[:N*N].reshape(N,N),X[N*N:].reshape(N,N)
dx = (x*(1.-x) - f*z*(x-q)/(x+q) + convolve2d(x,A,'same','wrap') )/ϵ
dz = x-z + convolve2d(z,B,'same','wrap')
return np.hstack([dx.flatten(),dz.flatten()])
#
sol = solve_ivp(ODEs,t_span,np.hstack([x.flatten(),z.flatten()]),'RK23',t_eval,rtol=1e-8,atol=1e-6)
for u in sol.y.T[:,:N*N]:
u = u.reshape(N,N)
fig,ax = plt.subplots(figsize=(4,4))
ax.imshow(u,cmap='jet')
plt.show()
2次元場PDE (応用編)
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
from scipy.signal import convolve2d
from scipy.integrate import solve_ivp
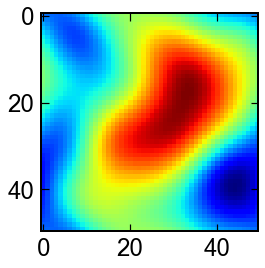
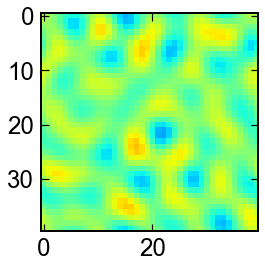
TDGLのスピノーダル分解
TDGLは時間依存ギンツブルグランダウの略です.オーダーパラメータ$\psi$の保存則が,
$$
\psi = (\partial_{xx}+\partial_{yy})\mu
$$
であり,$\mu$はGL-Wilsonハミルトニアンの$\psi$微分であって,
$$
\mu = - \psi + \psi^3 - (\partial_{xx}+\partial_{yy})\psi
$$
定数を除いて書けるとします. 初期条件として与えたノイズから成長するドメインを見てみましょう.
# parameter
N = Nx = Ny = 40
Δ = Δx = Δy = 1.0
D = (1.0/Δ**2)
A = np.array([[0.0, D,0.0],
[D ,-4*D, D],
[0.0, D,0.0],])
# init
Ψ = 2.0*(np.random.rand(N,N)-0.5)*0.1
Ψ -= Ψ.mean()
init = Ψ.flatten()
# time
t_span=[0.0,20.0]
t_eval=np.linspace(*t_span,3)
# ODEs
def ODEs(t,Ψ):
Ψ = Ψ.reshape(N,N)
μ = - Ψ + Ψ**3 - convolve2d(Ψ,A,'same','wrap')
dΨ = convolve2d(μ,A,'same','wrap')
return dΨ.flatten()
#
sol = solve_ivp(ODEs,t_span,init,'RK23',t_eval)
vmax,vmin = sol.y.max(),sol.y.min()
for Ψ in sol.y.T:
Ψ = Ψ.reshape(N,N)
fig,ax = plt.subplots(figsize=(4,4))
# ax.imshow(Ψ,cmap='jet')
ax.imshow(Ψ,cmap='jet',vmax=vmax,vmin=vmin)
plt.show()
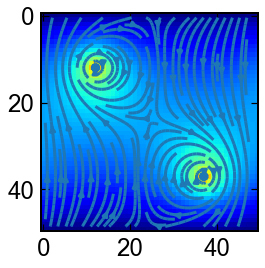
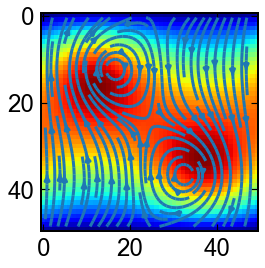
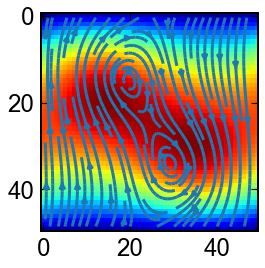
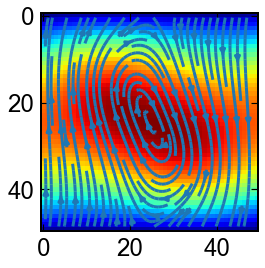
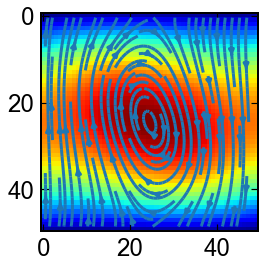
非圧縮性Navie-Stokes方程式
2次元に適用できる流れ関数渦度法を用いて,Navie-Stokes方程式の数値解の例を見てみましょう.
$$
\partial_{t}\omega + \partial_y \phi \partial_x\omega_x- \partial_x\phi\partial_y\omega
=\nu(\partial_{xx}+\partial_{yy})\omega
$$
$$
(\partial_{xx}+\partial_{yy})\phi=-\omega
$$
参考資料はこちら.
https://index-press.co.jp/books/digest/ceslib2.pdf
# parameter
N = Nx = Ny = 50
Δ = Δx = Δy = 1.0
s = N
C = np.diag(-4.0*np.ones(s*s )/Δ**2,k= 0) +\
np.diag(+1.0*np.ones(s*s-1)/Δ**2,k=-1) +\
np.diag(+1.0*np.ones(s*s-1)/Δ**2,k=+1) +\
np.diag(+1.0*np.ones(s*s-s)/Δ**2,k=-s) +\
np.diag(+1.0*np.ones(s*s-s)/Δ**2,k=+s)
#
Re=1.
# init
ω = np.zeros((N,N))
ω[N//4,N//4] =1.0 # vor1
ω[3*N//4,3*N//4]=1.0 # vor2
init = ω.flatten()
# time
t_span=[0.0,80.0]
t_eval=np.linspace(*t_span,5)
# ODEs
def ODEs(t,ω):
ψ = np.linalg.solve(C,-ω).reshape(N,N)
ω = ω.reshape(N,N)
dω = np.zeros((N,N))
dω[1:-1,1:-1] = 0.25/Δ**2*(ψ[2:]-ψ[:-2])[:,1:-1]*(ω[:,2:]-ω[:,:-2])[1:-1,:] + \
(1.0/Re)*(np.diff(ω,2,axis=0)[:,1:-1]/Δ**2+np.diff(ω,2,axis=1)[1:-1,:]/Δ**2)
return dω.flatten()
#
sol = solve_ivp(ODEs,t_span,init,'RK23',t_eval)
初期状態で与えた渦が合体して一つの大きな渦になっていく
x = np.linspace(0.,N-1,N)
x = 0.5*(x[1:]+x[:-1])
xx,yy = np.meshgrid(x,x)
for ω in sol.y.T:
ψ = np.linalg.solve(C,-ω).reshape(N,N)
vx,vy = np.diff(ψ,1,1)/Δ, -np.diff(ψ,1,0)/Δ
fig,ax = plt.subplots(figsize=(4,4))
ax.streamplot(xx,yy,0.5*(vx[1:,:]+vx[:-1,:]).T,0.5*(vy[:,1:]+vy[:,:-1]).T,cmap='jet')
ax.imshow(np.abs(ψ),cmap='jet')
plt.show()
あとがき
初投稿ですが記事書くのって難しいですね...
git-hub.pagesにも同じ内容のものをおきました.(というかこっちを先に作った)