LoginSignup
0
0

More than 3 years have passed since last update.

@MirrgieRiana(Riana Mirrgie)

fluorite-8　実装の軌跡　Part 2　中間言語と四則演算

Last updated at Posted at 2020-11-03

初回

←前回

インタプリタからコンパイラ（トランスコンパイラ）に

目標

前回ラストのpegjsコードは、実行すると機械語や中間コードなどにコンパイルされた何かではなく、計算結果が直接帰ってきます。

[開閉]
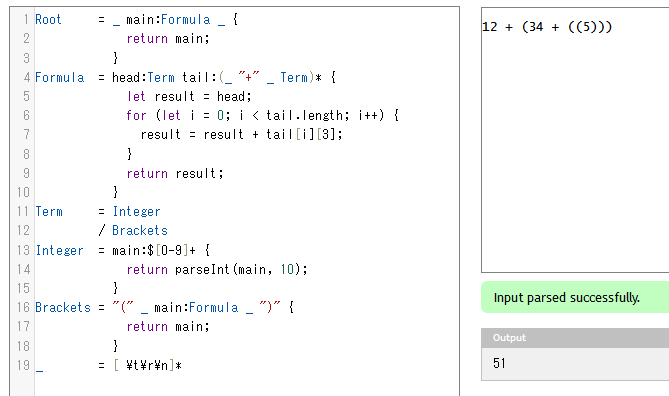
Root     = _ main:Formula _ {
             return main;
           }
Formula  = head:Term tail:(_ "+" _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = result + tail[i][3];
             }
             return result;
           }
Term     = Integer
         / Brackets
Integer  = main:$[0-9]+ {
             return parseInt(main, 10);
           }
Brackets = "(" _ main:Formula _ ")" {
             return main;
           }
_        = [ \t\r\n]*

image.png

柔軟さや実装の簡単さ的にはこれでよいですが、この方法でプログラミング言語を実装していくと、経験的に色々と悩まされることになります。これを解決するために、パーサの挙動をインタプリタ型からコンパイラ型に変更します。

目標としては、

入力
100 + 20 * 3 ^ 5

というfluorite-8コードを入力したら、

中間コード
((100) + ((20) * (Math.pow((3), (5)))))

というJavaScriptコードが出てきてくれたら嬉しいです。

中間言語としてJavaScriptを生成する利点は次のようなものです。

  • コンパイル処理が多少重くても実行速度はそれに影響されない。
  • 中間コード自体はJavaScriptと同じ速度で実行できる。
  • evalで簡単に実行できる。
  • コンパイル結果を文字列として自然に保存できる。
  • コンパイル済みのコードを一般的なJavaScriptから直接呼び出しできる。
  • 文字列を結合するだけで生成できる。
  • 変数や関数を生成する命令が簡潔に記述できる。
  • JavaScriptの関数を呼び出せる。
  • 一応人力で読める。

そこで、中間言語にコンパイルして、それを実行するようにしてみます。

コンパイラにした

できました。

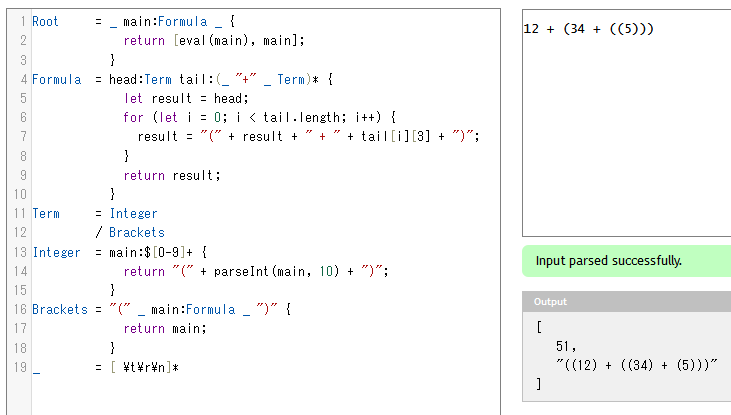
Root     = _ main:Formula _ {
             return [eval(main), main];
           }
Formula  = head:Term tail:(_ "+" _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = "(" + result + " + " + tail[i][3] + ")";
             }
             return result;
           }
Term     = Integer
         / Brackets
Integer  = main:$[0-9]+ {
             return "(" + parseInt(main, 10) + ")";
           }
Brackets = "(" _ main:Formula _ ")" {
             return main;
           }
_        = [ \t\r\n]*

image.png

入力
12 + (34 + ((5)))

というfluorite-8コードを入力したら、

中間コード
((12) + ((34) + (5)))

という文字列が得られました。

変更箇所

Integerにおいて、
return parseInt(main, 10);が
return "(" + parseInt(main, 10) + ")";になりました。

数値は文字列化され、括弧で囲まれました。これで数値からJavaScriptコードを表す文字列になりました。Integerは、先頭と末尾が( )であるJavaScriptコード断片である文字列です。ちなみにわざわざ文字列を数値化して文字列化する理由は、先頭のゼロの扱いが異なるためです。

Formulaにおいて、
result = result + tail[i][3];が
result = "(" + result + " + " + tail[i][3] + ")";になりました。

Formulaも先頭と末尾が( )であるJavaScriptコード断片である文字列です。よって、Termもそういうデータなので、resultもtail[i][3]もそういうデータです。"(" + result + " + " + tail[i][3] + ")"部分は、((何か) + (何か))という形の文字列になるということになります。

Rootが中間コードとその実行結果を返すように変わりました。

減算の追加

目標

現状のFormula

現状
Formula  = head:Term tail:(_ "+" _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = "(" + result + " + " + tail[i][3] + ")";
             }
             return result;
           }

は+演算子しか受け付けません。

これを、-演算子を入力したら中間コード側にも-演算子が現れるようにしたいと思います。

戦略

減算を受け入れるには、以下の変更が必要です。

  1. 演算子定義の部分が+でも-でもマッチするようにする。
  2. どちらにマッチしたかで出力を変える。

1を満たすには、1行目の"+"が("+" / "-")となればよいです。

2を満たすには、4行目の" + "が、tail[i][1]の値によって変わるようになっていればよいです。

実装

Formula  = head:Term tail:(_ (
             "+"
           / "-"
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               let operator;
               if (tail[i][1] === "+") operator = "+";
               if (tail[i][1] === "-") operator = "-";
               result = "(" + result + " " + operator + " " + tail[i][3] + ")";
             }
             return result;
           }

これで減算に対応しました。

image.png

乗除算の追加

目標

ここまでで+ -演算子が実装されました。さらに* /演算子も実装したいと思います。

乗除算は加減算よりも優先的に結合し、項を作ります。

戦略

ここまでのPEG.jsコードはこれです。

現状
Root     = _ main:Formula _ {
             return [eval(main), main];
           }
Formula  = head:Term tail:(_ (
             "+"
           / "-"
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               let operator;
               if (tail[i][1] === "+") operator = "+";
               if (tail[i][1] === "-") operator = "-";
               result = "(" + result + " " + operator + " " + tail[i][3] + ")";
             }
             return result;
           }
Term     = Integer
         / Brackets
Integer  = main:$[0-9]+ {
             return "(" + parseInt(main, 10) + ")";
           }
Brackets = "(" _ main:Formula _ ")" {
             return main;
           }
_        = [ \t\r\n]*

目標を達成するには、次のように定義を変えればよいです。

現状
Termは、「IntegerもしくはBrackets」である。

↓

改変後
Termは、「IntegerもしくはBrackets」もしくは複数のそれらが1個以上の「"*"もしくは"/"」で結合されたものである。

より簡単にいうと、

改変後
Termは、1個以上の「IntegerもしくはBrackets」が「"*"もしくは"/"」で結合されたものである。

より実装内容に沿った言い方をすると、

改変後
Termは、1個のFactorの後に、0個以上の「「"*"もしくは"/"」およびFactor」が続いたものである。
Factorは、IntegerもしくはBracketsである。

となります。

実装

できました。

Root     = _ main:Formula _ {
             return [eval(main), main];
           }
Formula  = head:Term tail:(_ (
             "+"
           / "-"
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               let operator;
               if (tail[i][1] === "+") operator = "+";
               if (tail[i][1] === "-") operator = "-";
               result = "(" + result + " " + operator + " " + tail[i][3] + ")";
             }
             return result;
           }
Term  = head:Factor tail:(_ (
             "*"
           / "/"
           ) _ Factor)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               let operator;
               if (tail[i][1] === "*") operator = "*";
               if (tail[i][1] === "/") operator = "/";
               result = "(" + result + " " + operator + " " + tail[i][3] + ")";
             }
             return result;
           }
Factor   = Integer
         / Brackets
Integer  = main:$[0-9]+ {
             return "(" + parseInt(main, 10) + ")";
           }
Brackets = "(" _ main:Formula _ ")" {
             return main;
           }
_        = [ \t\r\n]*

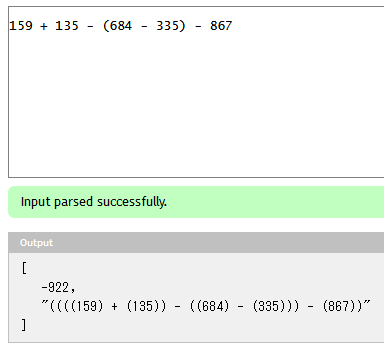
(53 + 42 * 86 / 10 / 48 - 29 * 48) / (7 - (8 + 9) * 10) * 86

image.png

オペレータ定義を1行にまとめたい

目標

現状の演算子定義

現状
Formula  = head:Term tail:(_ (
             "+"
           / "-"
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               let operator;
               if (tail[i][1] === "+") operator = "+";
               if (tail[i][1] === "-") operator = "-";
               result = "(" + result + " " + operator + " " + tail[i][3] + ")";
             }
             return result;
           }

は、以下の点で不便です。

  1. 演算子を追加する度に離れた2か所の改変が必要。
  2. (Math.pow(a, b))のような凝った順序でトークンを挿入する演算を出力できない。

そこで、これを解決したいと思います。

戦略

2行目・3行目は現在記号1文字で構成された文字列を返しますが、これを2個のJSコードを取ってJSコードを返す関数が返るようにすればすべてうまくいきます。

実装

Formula  = head:Term tail:(_ (
             "+" { return (a, b) => "(" + a + " + " + b + ")"; }
           / "-" { return (a, b) => "(" + a + " - " + b + ")"; }
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }
Term  = head:Factor tail:(_ (
             "*" { return (a, b) => "(" + a + " * " + b + ")"; }
           / "/" { return (a, b) => "(" + a + " / " + b + ")"; }
           ) _ Factor)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }

これで演算子の追加が非常に簡単なものとなりました。

べき乗演算子^の追加

目標

  • a ^ bというfl8コードがMath.pow(a, b)というJavaScriptコードになる。
  • べき乗は乗除算よりも結合優先度が高い。
  • 右優先結合である。

戦略

安直な実装は次のものです。これは結合優先度の条件は満たしますが、右優先結合の条件を満たしません。

安直な実装
Pow  = head:Factor tail:(_ (
             "^" { return (a, b) => "(Math.pow(" + a + ", " + b + "))"; }
           ) _ Factor)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }

なぜ左優先結合（1+2+3+4が((1+2)+3)+4と解釈される）になるのかというと、最初に変数にheadを入れて、それをtailの先頭とくっつけていくからです。これに従って結合すると、構文木が左側に向かって深く伸びていきます。

なので、定義を以下のように変えます。

安直な実装
Powは、1個のFactorの後に、0個以上の「べき乗演算子およびFactor」が続いたものである。

↓

改変後
Powは、0個以上の「Factorおよびべき乗演算子」の後に、1個のFactorが続いたものである。

これに従って処理をtailに対してheadの末尾から順番にくっつけていくように改変すると、右優先結合の演算子の実装となります。

実装

できました。

Pow      = head:(Factor _ (
             "^" { return (a, b) => "(Math.pow(" + a + ", " + b + "))"; }
           ) _)* tail:Factor {
             let result = tail;
             for (let i = head.length - 1; i >= 0; i--) {
               result = head[i][2](head[i][0], result);
             }
             return result;
           }

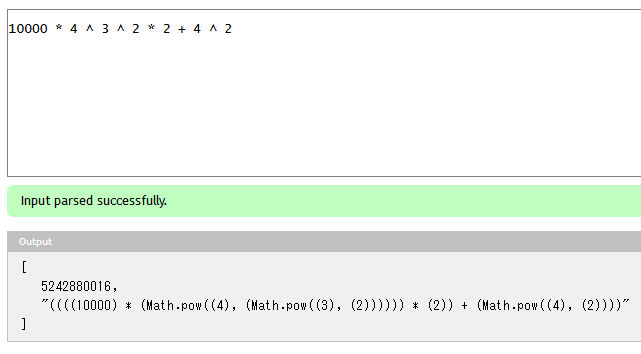
10000 * 4 ^ 3 ^ 2 * 2 + 4 ^ 2

image.png

まとめ

ここまでに出来上がったPEG.jsコードです。

[開閉]
Root     = _ main:Formula _ {
             return [eval(main), main];
           }
Formula  = head:Term tail:(_ (
             "+" { return (a, b) => "(" + a + " + " + b + ")"; }
           / "-" { return (a, b) => "(" + a + " - " + b + ")"; }
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }
Term  = head:Pow tail:(_ (
             "*" { return (a, b) => "(" + a + " * " + b + ")"; }
           / "/" { return (a, b) => "(" + a + " / " + b + ")"; }
           ) _ Pow)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }
Pow      = head:(Factor _ (
             "^" { return (a, b) => "(Math.pow(" + a + ", " + b + "))"; }
           ) _)* tail:Factor {
             let result = tail;
             for (let i = head.length - 1; i >= 0; i--) {
               result = head[i][2](head[i][0], result);
             }
             return result;
           }
Factor   = Integer
         / Brackets
Integer  = main:$[0-9]+ {
             return "(" + parseInt(main, 10) + ")";
           }
Brackets = "(" _ main:Formula _ ")" {
             return main;
           }
_        = [ \t\r\n]*

  • JavaScript中間コードを生成するようにすると色々恩恵があるので、それを採用した。
  • 減算のような同じ結合優先度の演算子を追加するには、-演算子を受理するようにして、それによって出力内容を変えればよい。
  • 乗除算のような異なる結合優先度の演算子を追加するには、ルールを増やせばよい。
  • 演算子が演算子を表す文字列ではなく関数を返すようにして、演算子の扱いを簡単にした。
  • べき乗のような右優先結合の演算子を追加するには、演算子の定義を前後逆にすればよい。

ここまでで、加減乗除べき乗括弧が入力できる言語のJavaScriptへのトランスコンパイラが出来ました。

次回→

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0