More than 3 years have passed since last update.

fluorite-8　実装の軌跡　Part 3　構文木の経由と符号

fluorite-8

Last updated at 2020-12-04Posted at 2020-11-04

構文解析と意味解析

前回ラストの段階では、構文解析と意味解析は同時に行われていました。ここでいう構文解析とは、ソースコードを記号がツリー状に結び付いた木構造データにすることで、意味解析はその木構造の各接点に意味を与えて中間コード生成などをすることです。

（一般的な意味解析の意味は型チェックとかのコンパイルエラーの判定だけれども、この言語のローカルルールでは、中置+が加算という挙動を行う、中置=の左辺は代入用の文脈として通常の式評価とは異なる解釈をする、といった解釈全般を意味解析として扱います。）

前回

Formula  = head:Term tail:(_ (
             "+" { return (a, b) => "(" + a + " + " + b + ")"; }
           / "-" { return (a, b) => "(" + a + " - " + b + ")"; }
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }

ここで、Formulaが返す値は演算子やリテラルが樹状に結び付いたデータではなく、既に中間コードとなるJavaScript文字列です。

その源流をたどると、"+" { return (a, b) => "(" + a + " + " + b + ")"; }の部分で既に中間コードを出力するようになっています。もしここが構文木を出力するようになっていたら、Formulaも構文木を返すようになります。

構文解析部分と意味解析部分の分離

このコードでは構文解析部分と意味解析部分は分かれておらず、一つのステップで両方が行われます。

これらの処理を分離すると次のような利点があるので、分離を行います。

ソースコードが機能の面で分割される。
意味解析の挙動を変える際にPEG.js部分のコードを弄る必要がない。
構文木をJSONなどで保存しておくことができる。

中間コードではなく構文木オブジェクトを出力する

出来ました。このコードではTermの値が構文木オブジェクトであることを想定しています。構文木オブジェクトは、typeに演算子やリテラルの種類を、argumentに演算子の項やリテラルの値を保持したJavaScriptオブジェクトです。

改変後

Root     = _ main:Formula _ {
             return main;
           }

Formula  = head:Term tail:(_ (
             "+" { return (a, b) => {type: "plus", argument: [a, b]}; }
           / "-" { return (a, b) => {type: "minus", argument: [a, b]}; }
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = tail[i][1](result, tail[i][3]);
             }
             return result;
           }

Integer  = main:$[0-9]+ {
             return {type: "integer", argument: main};
           }

Formulaの演算子定義の関数が構文木オブジェクトを返すようになっています。これにより、Formulaが返す値も構文木オブジェクトです。

Integerも数値ではなく構文木オブジェクトが返るようになりました。argumentには整数を表す文字列が格納されています。

Rootはここでは一旦構文木をそのまま返すことにしておきます。

整理

オブジェクト生成の部分をtoken関数に分離し、演算子定義の部分を演算子名だけを返すように変えました。PEG.jsではルール列の前に{ }で囲まれたJavaScriptを置くことができ、そこで定義されたものをルールのアクションから利用できます。

整理後

{
  function token(type, argument) {
    return {type, argument};
  }
}

Root     = _ main:Formula _ {
             return main;
           }

Formula  = head:Term tail:(_ (
             "+" { return "plus"; }
           / "-" { return "minus"; }
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = token(tail[i][1], [result, tail[i][3]]);
             }
             return result;
           }

Integer  = main:$[0-9]+ {
             return token("integer", main);
           }

ここでは意味解析を排除しているので、^がべき乗を表すのか、ビットXORを表すのかは認知しません。なので、演算子名には演算の種類ではなく、記号の名前を書いてあります。

**以降、トークンという言葉は「構文解析上不可分な文字のシーケンス」ではなく、「構文木上の一つの節」を表すことにします。**例えば(1 + 2)は全体が丸括弧( )というトークンです。

意味解析の実装

これまでは生成されたものはJavaScriptコードだったので、単にevalをすれば評価できました。しかし、今は構文木オブジェクトが生成されているので、このままでは評価できません。

なので、構文木オブジェクトをJavaScriptコードに変換する部分を作ります。構文解析部分が分離されたおかげで、これはPEG.jsとは直接関係のないただのJavaScriptのコードです。

意味解析

{
  const registry = {};
  registry.integer = argument => "(" + parseInt(argument, 10) + ")";
  registry.plus = argument => "(" + compile(argument[0]) + " + " + compile(argument[1]) + ")";
  registry.minus = argument => "(" + compile(argument[0]) + " - " + compile(argument[1]) + ")";
  registry.asterisk = argument => "(" + compile(argument[0]) + " * " + compile(argument[1]) + ")";
  registry.slash = argument => "(" + compile(argument[0]) + " / " + compile(argument[1]) + ")";
  registry.circumflex = argument => "(Math.pow(" + compile(argument[0]) + ", " + compile(argument[1]) + "))";
  function compile(token) {
    return registry[token.type](token.argument);
  }
}

構文木オブジェクトをcompile関数に入れるとJavaScriptコードが出てきます。

構文解析と意味解析が分離されたお陰で、どんな種類のトークンがどのような挙動をするのかが一か所にまとめられて管理がしやすくなりました。

また、新たな演算子を追加する際にも、構文解析部分はトークンを受理して構文木オブジェクトを作るだけで良いです。意味解析部分も演算子の見た目に依存せず、演算の挙動だけを考えれば良いです。

この章のまとめ

ここまでのPEG.jsコード全文です。このコードは、評価結果・中間コード・構文木を出力します。

**[開閉]**

章まとめ

{
  const registry = {};
  registry.integer = argument => "(" + parseInt(argument, 10) + ")";
  registry.plus = argument => "(" + compile(argument[0]) + " + " + compile(argument[1]) + ")";
  registry.minus = argument => "(" + compile(argument[0]) + " - " + compile(argument[1]) + ")";
  registry.asterisk = argument => "(" + compile(argument[0]) + " * " + compile(argument[1]) + ")";
  registry.slash = argument => "(" + compile(argument[0]) + " / " + compile(argument[1]) + ")";
  registry.circumflex = argument => "(Math.pow(" + compile(argument[0]) + ", " + compile(argument[1]) + "))";
  function compile(token) {
    return registry[token.type](token.argument);
  }
  function token(type, argument) {
    return {type, argument};
  }
}
Root     = _ main:Formula _ {
             const token = main;
             const code = compile(main)
             const result = eval(code);
             return [result, code, token];
           }
Formula  = head:Term tail:(_ (
             "+" { return "plus"; }
           / "-" { return "minus"; }
           ) _ Term)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = token(tail[i][1], [result, tail[i][3]]);
             }
             return result;
           }
Term  = head:Pow tail:(_ (
             "*" { return "asterisk"; }
           / "/" { return "slash"; }
           ) _ Pow)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = token(tail[i][1], [result, tail[i][3]]);
             }
             return result;
           }
Pow      = head:(Factor _ (
             "^" { return "circumflex"; }
           ) _)* tail:Factor {
             let result = tail;
             for (let i = head.length - 1; i >= 0; i--) {
               result = token(head[i][2], [head[i][0], result]);
             }
             return result;
           }
Factor   = Integer
         / Brackets
Integer  = main:$[0-9]+ {
             return token("integer", main);
           }
Brackets = "(" _ main:Formula _ ")" {
             return main;
           }
_        = [ \t\r\n]*

出力例は次のようになります。

入力

2 / (2 - 8) * 456 ^ 5 + 5

出力

[
   -6572081774587,
   "((((2) / ((2) - (8))) * (Math.pow((456), (5)))) + (5))",
   {
      "type": "plus",
      "argument": [
         {
            "type": "asterisk",
            "argument": [
               {
                  "type": "slash",
                  "argument": [
                     {
                        "type": "integer",
                        "argument": "2"
                     },
                     {
                        "type": "minus",
                        "argument": [
                           {
                              "type": "integer",
                              "argument": "2"
                           },
                           {
                              "type": "integer",
                              "argument": "8"
                           }
                        ]
                     }
                  ]
               },
               {
                  "type": "circumflex",
                  "argument": [
                     {
                        "type": "integer",
                        "argument": "456"
                     },
                     {
                        "type": "integer",
                        "argument": "5"
                     }
                  ]
               }
            ]
         },
         {
            "type": "integer",
            "argument": "5"
         }
      ]
   }
]

符号の追加

目標

ここまでで二項演算子を5種類追加しましたが、この言語はまだ2 * (-2)という式を受理することができません。

以下の特徴を追加します。

符号を表す前置単項演算子+および-

結合優先度についての議論

符号の結合優先度はどうすればいいでしょうか。演算子同士の結合優先度を比較する際には、括弧を付けずに同居させてみると良いです。

-1 * -2 * -3

は

(-1) * (-2) * (-3)

と考えられるため、「符号演算子＞乗除演算子」は確定とします。

べき乗との比較はどうでしょうか。

テストケース

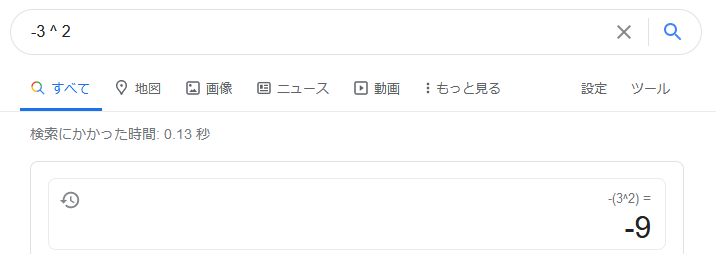
-3 ^ 2

Perl

$ perl -e 'print -3 ** 2'
-9

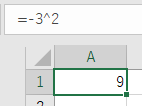
なんか処理系によってまちまちです。多分-9派は次のような数式に倣って符号よりもべき乗の優先度が高いです。

-3^2 = -9

前作fl7では、「前置系演算子はあらゆる中置系演算子に先行する」ポリシーにより、9派です。

$ fl7 '-3 ^ 2'
9

これはfl7に前置系演算子が結構いっぱいあるための仕様です。

同じく前置系演算子の種類が多く、べき乗演算子が存在するRakuではどうなっているのかというと、べき乗が前置系に先行するため、論理値化?がべき乗に負けています。

Raku

$ perl6 -e 'say ?3'
True
$ perl6 -e 'say ?3 ** 2'
True
$ perl6 -e 'say True ** 2'
1

fl8では、Rakuに倣ってべき乗はすべての前置系演算子よりも優先的ということにします。~~どうせJavaScriptでビットXORなんか滅多に使わないし困んないだろｗ~~

戦略

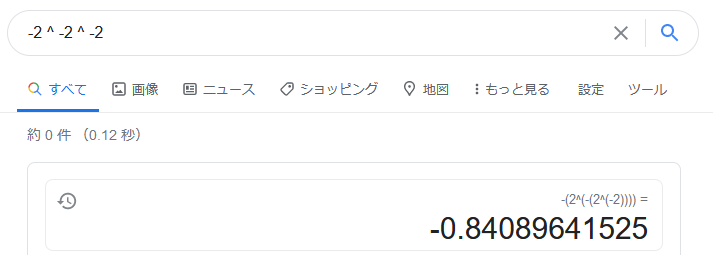
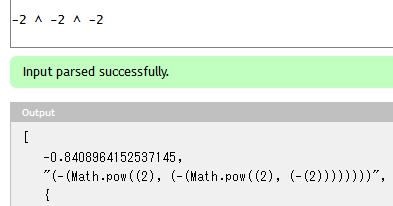
具体的にべき乗と符号の定義がどうであればよいのでしょうか。Googleは、前置-と中置^だけを使って、( )なしでループできるようになっています。

  -2 ^ -2 ^ -2
= -(2 ^ -(2 ^ -2))

^の左辺には符号付きの構文を直接置けませんが、右辺になら置けます。^は左右で文法が異なることになります。

符号付き構文をLeftとしたとき、Leftには^が含まれることがあります。含まれないこともあります。

合わせると次のような文法が浮かびます。なぜ^演算子は2 ^ 2 ^ 2のようにいくつも並べて書けるのにPowはFactor ("^" Left)*ではないのかというと、2 ^ 2 ^ 2の右側の^はPow = Factor "^" LeftのLeftに吸われるため、"^" Left部分は高々1回しか反復されないからです。このように、再帰的な参照関係をもつ文法の定義は繰り返しによる定義と等価だったりします。

Root   = Left
Left   = "-"* Pow
Pow    = Factor "^" Left
       / Factor
Factor = [0-9]+

実装

できました。

  registry.left_plus = argument => "(+" + compile(argument[0]) + ")";
  registry.left_minus = argument => "(-" + compile(argument[0]) + ")";

Term  = head:Left tail:(_ (
             "*" { return "asterisk"; }
           / "/" { return "slash"; }
           ) _ Left)* {
             let result = head;
             for (let i = 0; i < tail.length; i++) {
               result = token(tail[i][1], [result, tail[i][3]]);
             }
             return result;
           }
Left     = head:((
             "+" { return "left_plus"; }
           / "-" { return "left_minus"; }
           ) _)* tail:Pow {
             let result = tail;
             for (let i = head.length - 1; i >= 0; i--) {
               result = token(head[i][0], [result]);
             }
             return result;
           }
Pow      = head:Factor _ operator:(
             "^" { return "circumflex"; }
           ) _ tail:Left {
             return token(operator, [head, tail]);
           }
         / Factor

ちゃんとGoogleと同じ構文木になっています。

再帰を使わなくても多分下のような文法で構文木の組み立て方を工夫する方法がありますが、ここでは見送ります。

LeftPow = "-"* Factor ("^" "-"* Factor)*

定数の追加

目標

PIと書いたらMath.PI = 3.1415...を指すようにしたい。
それ以外の識別子はコンパイルエラーにしたい。

戦略

定数を提供するための機構は様々に考えられますが、ここではとりあえず識別子を定義し、識別子の挙動として、識別子の値がPIだった場合にMath.PIに相当する数値を中間コードに埋め込むようにしておきます。

実装

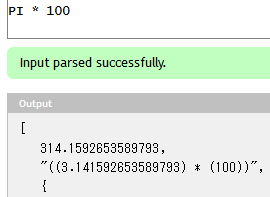
出来ました。

  registry.identifier = argument => {
    if (argument === "PI") return "(" + Math.PI + ")";
    throw new Error("Unknown identifier");
  };

Factor   = Integer
         / Identifier
         / Brackets
Identifier = main:$([a-zA-Z_] [a-zA-Z0-9_]*) {
             return token("identifier", main);
           }

PI以外の識別子が現れた場合、コンパイル時点でエラーになります。

3.141592653589793という値が埋め込まれていますが、これは飽くまでJavaScriptの式なので、実装によって実行時に何らかの計算を行うような挙動にすることもできます。

まとめ

ここまでに出来上がったPEG.jsコードです。