はじめに
こんにちは,(株)日立製作所 研究開発グループ サービスコンピューティング研究部の露木です。
機械学習で一般的な教師あり学習の問題として,正解ラベルの付いているデータを大量に準備しなければならないことが挙げられます。この問題を解決するために,ラベルなしデータを活用することで必要なラベル付きデータの数を削減する半教師あり学習の分野があります。そして,半教師あり学習の一種にグラフベースのラベル伝播法があります。
ラベル伝播法は,あるデータのラベルをその近傍にあるラベルのないデータにコピーする (伝播させる) ことで,少量のラベル付きデータからモデルを学習します。また,「グラフベース」と呼ばれる理由は,ひとつひとつのデータをノード,データの類似度をエッジ (の重み) としたグラフを構成して,このグラフ上でラベルを伝播するからです。このとき,類似度の計算にカーネル法を組み合わせることで非線形データにも対応可能になります。
scikit-learnの公式ドキュメント に記載されているように,scikit-learnにはラベル伝播法 (label propagation) とラベル拡散法 (label spreading) が実装されており,エンドユーザでも簡単に利用できる利点があります。このラベル伝播法とラベル拡散法の違いは類似度の計算方法にあり,ラベル拡散法では既存ラベルの変更を許します。例えばラベル拡散法でハイパーパラメータ $\alpha = 0.2$ を指定した場合は,全ラベルの 20% までは変更を許す条件で学習します。これはラベルの誤りを訂正できることを意味しますから,学習データに含まれるノイズに対してラベル拡散法のほうが頑健 (ロバスト) であるといえます。
そこで,本稿ではscikit-learnの例 をベースとした分類モデルの半教師あり学習の実行例を示し,ラベル伝播法と比較してラベル拡散法がノイズに頑健であることを確認します。なお,ソースコードはPython3のJupyterノートブックで実行することを想定しています。
実行例
環境準備
まず最初に依存ライブラリをインストールします。必要に応じて,下記のセルをコメントアウトして実行してください。
# !pip3 install sklearn numpy matplotlib
次にライブラリを読み込み,初期設定を行います。
import sklearn
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.semi_supervised import LabelPropagation
from sklearn.semi_supervised import LabelSpreading
from sklearn.datasets import make_circles
import random
import math
# 日本語でグラフ表示できるようにおまじない
font = {'family':'IPAexGothic'}
mpl.rc('font', **font)
# フォントサイズを大きくする
plt.rcParams['font.size'] = 12
# 画像サイズを指定
plt.rcParams["figure.figsize"] = (4, 4)
データ準備
人工的なデータセットを作成していきます。今回は二重丸の形状をしたデータセットにノイズを加えて利用します。作成条件のパラメータは以下の通りです。
# データセット作成時のパラメータ
n_samples = 400 # 全データ数
factor = 0.4 # 内側の輪の直径を指定する係数
label_rate = 0.2 # 学習に利用するラベル付きデータの割合
flip_rate = 0.1 # ラベルに加えるノイズ (ラベルを反転させる確率)
noise = 0.05 # 特徴量に加えるノイズ (ガウシアンノイズの強さ)
random_state = random.randint(1, 1000) # 乱数のシードを指定して再現性を保つ
設定したパラメータを使ってデータセットを作成します。
# データセットを作成
X, y = make_circles(n_samples=n_samples, noise=noise, factor=factor,
shuffle=True, random_state=random_state)
次に,データセットから今回の実験に用いるラベル付きデータを選り分けて,学習データを作成します。
# 半教師あり学習に利用するラベル付きのデータの数
n_labeled = math.floor(n_samples * 0.5 * label_rate)
# ラベルの入れ物を作成
outer, inner = 0, 1
labels = np.full(n_samples, -1.)
# 半教師あり学習に利用する "inner" ラベルを作成
labels[np.where(y==inner)[0][0:n_labeled]] = [int(random.uniform(0, 1) >= flip_rate) for x in range(n_labeled)]
# 半教師あり学習に利用する "outer" ラベルを作成
labels[np.where(y==outer)[0][0:n_labeled]] = [int(random.uniform(0, 1) <= flip_rate) for x in range(n_labeled)]
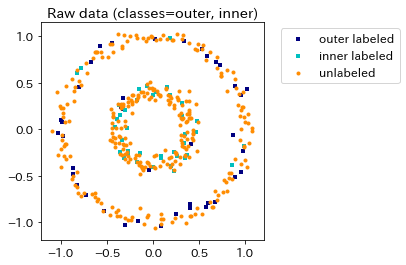
作成した学習データの分布を可視化します。加えたノイズの大きさを確認してください。本来は2つの真円からなる二重丸型の分布になるはずですが,ガウシアンノイズにより真円から歪んでおり,また一部のラベルが反転していることが見て取れます。
plt.scatter(X[labels == outer, 0], X[labels == outer, 1], color='navy',
marker='s', lw=0, label="outer labeled", s=10)
plt.scatter(X[labels == inner, 0], X[labels == inner, 1], color='c',
marker='s', lw=0, label='inner labeled', s=10)
plt.scatter(X[labels == -1, 0], X[labels == -1, 1], color='darkorange',
marker='.', label='unlabeled')
plt.legend(scatterpoints=1, shadow=False,
loc='upper left', bbox_to_anchor=(1.05, 1))
plt.title("Raw data (classes=outer, inner)")
plt.show()
学習の実行
まずはラベル伝播法で学習します。k近傍法 (KNN, K-nearest neighbor algorithm)を用いたラベル伝播法では,近傍のデータ数 n_neighbors がハイパーパラメータになります。n_neighborsの数が大きいほど,多数の近傍データについて平均したラベルを伝播することになります。これにより,(ラベル付きデータの数が十分に多ければ) ノイズに頑健になります。
今回は n_neighbors = 7 で学習を実行します。
kernel = 'knn'
n_neighbors = 7
label_prop = LabelPropagation(kernel=kernel, max_iter=1000, n_jobs=-1, n_neighbors=n_neighbors)
label_prop.fit(X, labels)
次に,ラベル拡散法で学習します。ラベル拡散法ではn_neighborsに加えて,$\alpha$ がハイパーパラメータになります。$\alpha$ の値は,もともと付いていたラベルをラベル拡散法の結果で置き換える割合を示します。$\alpha = 0$ ならば全てのラベルを保持することを意味し,$\alpha = 1$ ならば全てのラベルを置き換えることになります。0ではない $\alpha$ の設定は元のラベルを信用しないことを意味するため,適切な $\alpha$ の設定によってノイズに頑健になります。
alpha = 0.2
n_neighbors = 7
kernel = 'knn'
label_spread = LabelSpreading(kernel=kernel, alpha=alpha, n_neighbors=n_neighbors,
max_iter=1000, n_jobs=-1)
label_spread.fit(X, labels)
ラベル伝播法とラベル拡散法の分類精度(accuracy)を比較します。$\alpha$ の効果によって反転したラベルを訂正できるため,ラベル伝播法よりもラベル拡散法のほうが高精度になっていることがわかります。
print("ラベル伝播法の精度 (accuracy) = %.2f" % (label_prop.score(X, y)))
print("ラベル拡散法の精度 (accuracy) = %.2f" % (label_spread.score(X, y)))
ラベル伝播法の精度 (accuracy) = 0.52
ラベル拡散法の精度 (accuracy) = 0.94
結果の可視化
精度だけでは実際の分類結果が不明なため,散布図として可視化します。
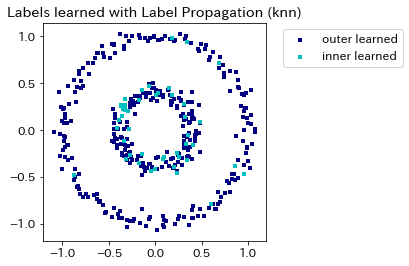
まず,ラベル伝播法による分類結果は以下のようになります。今回,作成したデータセットのように,ノイズが強い場合や利用可能なラベル付きデータの数が少ない場合,正しくinnerラベルとouterラベルのデータを分類できないことがわかります。
# ラベル伝播法の学習結果をグラフ化
output_labels_prop = label_prop.transduction_
output_label_array = np.asarray(output_labels_prop)
outer_numbers = np.where(output_label_array == outer)[0]
inner_numbers = np.where(output_label_array == inner)[0]
plt.scatter(X[outer_numbers, 0], X[outer_numbers, 1], color='navy',
marker='s', lw=0, s=10, label="outer learned")
plt.scatter(X[inner_numbers, 0], X[inner_numbers, 1], color='c',
marker='s', lw=0, s=10, label="inner learned")
plt.legend(scatterpoints=1, shadow=False,
loc='upper left', bbox_to_anchor=(1.05, 1))
plt.title("Labels learned with Label Propagation (%s)" %(kernel))
plt.show()
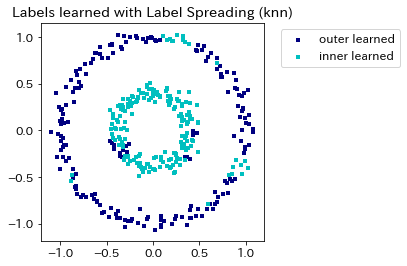
次に,ラベル拡散法による分類結果を確認します。精度の値に対応し,ラベル伝播法と比較して ラベル拡散法は innerラベル とouterラベルを精度良く分類できることがわかります。
# ラベル拡散法の学習結果をグラフ化
output_labels_spread = label_spread.transduction_
output_label_array = np.asarray(output_labels_spread)
outer_numbers = np.where(output_label_array == outer)[0]
inner_numbers = np.where(output_label_array == inner)[0]
plt.scatter(X[outer_numbers, 0], X[outer_numbers, 1], color='navy',
marker='s', lw=0, s=10, label="outer learned")
plt.scatter(X[inner_numbers, 0], X[inner_numbers, 1], color='c',
marker='s', lw=0, s=10, label="inner learned")
plt.legend(scatterpoints=1, shadow=False,
loc='upper left', bbox_to_anchor=(1.05, 1))
plt.title("Labels learned with Label Spreading (%s)" %(kernel))
plt.show()
おわりに
今回示した例のようにラベル伝播法・拡散法を用いれば少量のラベル付きデータから分類モデルを学習できます。また,ラベル拡散法であれば,学習データのノイズに強いことも示しました。一方で,ラベル伝播法・拡散法のような半教師あり学習のアルゴリズムを用いるということは「特徴量空間において近い位置にあるデータは同じラベルに属する」という仮定をおいて学習を進めることになります。このような仮定が常に成立するとは限らないため,実適用の際にはデータセットや分類結果の丁寧な可視化による確認が重要といえます。