はじめに
こんにちは、(株)日立製作所 研究開発グループ サービスコンピューティング研究部の露木です。
画像認識や自然言語処理などの問題を教師あり学習の枠組みで解く場合,大量のデータを収集し,正解ラベルを付与して学習データを作成する必要があります。この学習データ作成の工数を削減するために,能動学習と呼ばれる技術があります。
能動学習は,モデルの高精度化に有効なラベルなしデータから順に選択して学習する技術です。これにより,ラベルなしデータへのラベル付け作業 (アノテーション) 数を削減し,ひいては学習データの作成コストを削減できます。
本記事では能動学習の概要を説明した上で,実行可能なソースコードと実行結果をご紹介します。
能動学習の概要
機械学習で最も一般的な「教師あり学習」では,複数の特徴量 $x_1,x_2,x_3 \cdots $ からなる特徴量ベクトル $\bf x$ と,ラベル $y$ で構成される学習データ $\{ {\bf x}_i,y_i \}$ を用いてモデルを学習します。ただし,$i$ はデータを区別するためのIDです。例えば,工場の検査工程を自動化するために,不良品の判定モデルをつくりたいときは製品の検査データ (外観の写真や,重さなど,センサーで測定可能な情報) が特徴量 $x$ に相当し,実際にその製品が不良品だったのか,あるいは良品だったのか,という情報がラベル $y$ に相当します。
表1. 作成すべき学習データ
| $i$ | 特徴量$x_1$ | 特徴量$x_2$ | 特徴量$x_3$ | ... | ラベル$y$ |
|---|---|---|---|---|---|
| 1 | 0.1 | 9 | 3.2 | ... | 1 |
| 2 | 2.3 | 2 | 3.2 | ... | 0 |
| 3 | 0.9 | 12 | 3.2 | ... | 0 |
今,不良品の判定モデルを学習するために,学習データ $\{ {\bf x}_i,y_i \}$ を作ることを考えます。特徴量 ${\bf x}$ はセンサーを設置さえすれば自動的に測定可能ですが,ラベル $y$ は人間が確認して不良品なら1,良品なら0と手入力しなければなりません。精度の良いモデルを作るためには一般に大量の学習データが必要ですから,学習データを作成する手間が大きくなってしまいます。
表2. 自動的に測定できるラベルなしデータ
| $i$ | $x_1$ | $x_2$ | $x_3$ | ... |
|---|---|---|---|---|
| 1 | 0.1 | 9 | 3.2 | ... |
| 2 | 2.3 | 2 | 3.2 | ... |
| 3 | 0.9 | 12 | 3.2 | ... |
そこで能動学習では,与えられたモデルを高精度化するのに必要な少数のサンプルを選び出すことで,学習データの作成コストを低減します。サンプル選択の基準には,おおよそ下記の6種類があります。 1
- Uncertainty Sampling
- Query-By-Committee
- Expected Model Change
- Expected Error Reduction
- Variance Reduction
- Density-Weighted Methods
今回は,上記のなかでもっとも広く使われているUncertainty Samplingを用います。Uncertainty Samplingでは以下の式にもとづいて「分類結果についてモデルが最も自信のないサンプル${\bf x}^*$」を選択します。モデルが苦手なサンプルから答えを教えていけば,効率的に高精度化できるだろうという考え方です (least confident法) 。
$$
{\bf x}^* = \arg \max_{\bf x} { 1 - P(\hat{y}| {\bf x})}
$$
ただし,$P(y|{\bf x}_i)$ はモデルがサンプル ${\bf x}_i$ を クラス $y$ に分類する確率であり,クラス $\hat{y}$ は複数あるクラスのうち分類確率が最大のクラスです。
$$
\hat{y} = \arg \max_y P(y| {\bf x})
$$
今回の不良品を判定するモデルの場合は,クラスは不良品か良品の2種類,つまり $y=0$ か $y=1$ しかないので,least confident法で選び出すサンプル${\bf x}^*$は不良品・良品ともに分類確率50%となり,どちらとも言えないようなサンプルに相当します。例えば,下記のように$i$番目のサンプルの$y=0$への分類確率 $P(0| {\bf x}_i)$が計算された場合,3番目 $(i=3)$ のサンプルが選択されます。
表3. 能動学習の例。この場合,least confident法では $i=3$ のサンプルが選択される
| $i$ | $x_1$ | $x_2$ | $x_3$ | ... | $P(0\mid {\bf x}_i)$ | $P(1\mid {\bf x}_i)$ |
|---|---|---|---|---|---|---|
| 1 | 0.1 | 9 | 3.2 | ... | 0.1 | 0.9 |
| 2 | 2.3 | 2 | 3.2 | ... | 0.8 | 0.2 |
| 3 | 0.9 | 12 | 3.2 | ... | 0.6 | 0.4 |
サンプル${\bf x}^*$を選んだら,人間に問い合わせてラベル $y$ を入力してもらい,学習データを増やしていきます。なお,能動学習の分野ではこのラベルを入力する人間や機械を,すべての答えを知っている存在として神託 (oracle)と呼びます。
以上のように,能動学習を実施するためには,サンプル ${\bf x}$を測定する必要はありますが,ラベル付けするべきサンプル数を削減できるため,学習データの作成コストを低減できます。
能動学習の実行例
それでは実際に,能動学習の一通りの流れをPython3で体験してみます。今回は例として分類モデルのアルゴリズムにサポートベクトルマシーンを用いて,うずまき状のデータを上手く分類できるようにモデルを鍛えていきます。
実行環境の準備
least confident法であれば実装も簡単ですが別のアルゴリズムへの拡張を容易にするため,今回は能動学習ライブラリ ALiPy を機械学習ライブラリscikit-learn と組み合わせて使います。ライブラリをインストールするために,次のコマンドを実行してください。
pip3 install alipy sklearn numpy matplotlib
ライブラリのインポート
※ この節より先のコードはすべてPython3のソースコードです。JupyterノートブックかPythonスクリプトの内部で実行してください。
まず,Pythonライブラリを読み込みます。
import random
import matplotlib.pyplot as plt
import numpy
from sklearn.datasets.samples_generator import make_swiss_roll
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
from alipy.experiment import AlExperiment
from alipy.query_strategy import QueryInstanceUncertainty
from alipy.index import IndexCollection
from alipy.oracle import MatrixRepository
データセットの作成
サンプルデータとして用いる,うずまき状のデータセットを作成します。以下のコードを実行すると 二次元の特徴量空間に 500 x 2 = 1000個のデータを作成し,図示します。
今回は,図中に青色で示した "class 0" のデータと橙色の "class 1" のデータを正しく二値分類するモデルの学習を目指します。
# 特徴量の生成
n = 500 # データ点数
X_0, _ = make_swiss_roll(n_samples=n, noise=1, random_state=0)
X_1, _ = make_swiss_roll(n_samples=n, noise=1, random_state=0)
# 2次元配列にする
X_0 = X_0[:, [0,2]]
X_1 = X_1[:, [0,2]] * -1
# ラベルを生成する
y_0 = numpy.array([0] * n)
y_1 = numpy.array([1] * n)
# 一定の確率でラベルを反転するノイズを加える
flip_rate = 0.01
for x in range(n):
random.seed(2019)
if random.uniform(0, 1) <= flip_rate:
y_0[x] = 1
random.seed(2019)
if random.uniform(0, 1) <= flip_rate:
y_1[x] = 0
# データセットとしてまとめる
X = numpy.concatenate([X_0, X_1])
y = numpy.concatenate([y_0, y_1])
# 可視化
plt.clf()
plt.axes().set_aspect('equal')
plt.scatter(X[y==0,0], X[y==0,1], label="class 0", edgecolor='#555555')
plt.scatter(X[y==1,0], X[y==1,1], label="class 1", edgecolor='#555555')
plt.legend()
plt.show()
初期モデルの学習と評価
先程用意した1000個のデータのうち,30% (300個) をテストデータ,70% (700個) を学習データとして分離します。そのうえで,学習データの 20% (140個) をとりだし,初期学習データとして初期モデルを学習します。このコードの出力にあるように,初期モデルでは予測の正解率は低く,学習データ数の不足が予想されます。
# 初期学習データの準備
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=2019, shuffle=True)
train_indices = numpy.arange(len(X_train))
initial_rate = 0.2 # 全学習データの20%を初期学習データとする
numpy.random.seed(1991) # 乱択結果の再現性を保つためにシードを指定。
init_indices = numpy.random.choice(train_indices, int(initial_rate * len(X_train)) , replace=False)
# 初期モデルの学習
model = SVC(probability=True, gamma=0.05, C=1, random_state=2019)
model.fit(X_train[init_indices], y_train[init_indices])
# 正解率の計算
pred_test = model.predict(X_test)
init_accuracy = accuracy_score(y_test, pred_test)
print("%d個の初期データで正解率は %1.1f%%" %(int(initial_rate * len(X_train)), init_accuracy*100))
140個の初期データで正解率は 73.7%
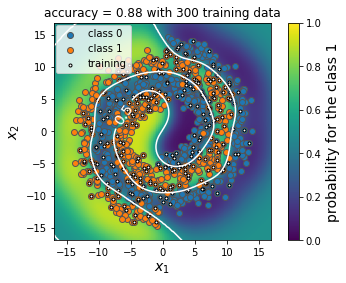
初期モデルによる分類結果を確認します。白色の小さなプロット点が初期学習データとして用いたサンプルであり,残りの青色やオレンジ色のプロット点は初期訓練データに含まれないデータ点です。Class 1の分類確率は,背景の密度プロットとして示しており,黄色に近いほどclass1に分類される確率が高いことを意味します。また,等高線図として,class0とclass1の分類確率が0.5になる分類境界も示しています。
図より,サンプル数の少ない初期訓練データでは分類モデルをうまく学習できていないことがわかります。
def plot_predict_results(model,X, y, X_train, accuracy):
'''
分類確率をプロットする関数
'''
# 分類確率を計算するためのGrid点を準備
lim = 17
x1 = numpy.arange(-lim, lim, 0.1)
x2 = numpy.arange(-lim, lim, 0.1)
x1,x2 = numpy.meshgrid(x1, x2)
xx = numpy.array([x1, x2]).T
# 分類確率を計算
Z = [model.predict_proba(k)[:,1] for k in xx]
# 密度プロットを描画
plt.clf()
plt.axes().set_aspect('equal')
plt.pcolormesh(x2, x1, Z, vmin=0, vmax=1)
pp = plt.colorbar()
pp.set_label("probability for the class 1", fontsize=14) #カラーバーのラベル
# 等高線図を描画
cont = plt.contour(x2,x1, Z, 1, levels=[0.5], vmin=0, vmax=1, colors=['white'])
cont.clabel(fmt='%1.1f', fontsize=14)
# 散布図として,全データセットを描画
plt.scatter(X[y==0,0], X[y==0,1], label="class 0", edgecolor='#555555')
plt.scatter(X[y==1,0], X[y==1,1], label="class 1", edgecolor='#555555')
# 訓練データを描画
xt = numpy.array(X_train)
plt.scatter(xt[:,0], xt[:,1], label="training", marker='.', c='w', edgecolor='k')
# 軸ラベル等の定義
plt.xlabel('$x_1$', fontsize=14)
plt.ylabel('$x_2$', fontsize=14)
plt.legend(bbox_to_anchor=(0.01, 0.99), loc='upper left', borderaxespad=0, fontsize=10, facecolor='w')
plt.title("accuracy = %1.2f with %d training data" % (accuracy, len(X_train)))
plt.show()
plot_predict_results(model, X, y, X_train[init_indices], init_accuracy)
能動学習による学習データの追加
学習データ数の追加に応じて,どのようにモデルの精度が向上するのか確認します。今回は,(1) least confident法による能動学習で学習データを追加する場合と (2)ランダムに学習データを追加する場合,の2通りについて計算を行います。
下記のコードを実行すると,300個を上限とした学習データの追加とモデルの学習を5回繰り返し,各時点におけるモデルの平均正解率を学習曲線として可視化します。グラフの縦軸は正解率 (accuracy),横軸は追加した学習データ数に相当します。グラフより,初期学習データのみでは75%程度の正解率であったモデルが,学習データの追加によって最終的に90%程度まで向上することがわかります。
また,能動学習を実行した場合 (グラフ中のactive learning) はランダム選択した場合 (グラフ中のrandom) よりも収束が早く,少ない学習データでより良いモデルを得られていると言えます。
from alipy.experiment import ExperimentAnalyser
analyser = ExperimentAnalyser()
# 初期学習データの準備
# X, y = load_wine(return_X_y=True)
al = AlExperiment(X, y,
model=SVC(probability=True, gamma=0.05, C=1, random_state=2019),
stopping_criteria='num_of_queries', stopping_value=300, batch_size=1)
al.split_AL(initial_label_rate=0.2, test_ratio=0.3, split_count=5)
# 能動学習の場合
al.set_query_strategy(strategy="QueryInstanceUncertainty", measure='least_confident')
al.set_performance_metric('accuracy_score')
al.start_query(multi_thread=False, verbose=False)
analyser.add_method(method_name='active learning', method_results=al.get_experiment_result())
# ランダム追加の場合
al.set_query_strategy(strategy="QueryInstanceRandom")
al.set_performance_metric('accuracy_score')
al.start_query(multi_thread=False, verbose=False)
analyser.add_method(method_name='random', method_results=al.get_experiment_result())
# 学習曲線を可視化
n_init = len(al._label_idx[0])
analyser.plot_learning_curves(title="Learning Curve", show=True,
std_area=True, std_alpha=0.2, saving_path=None,
x_shift=n_init)
能動学習結果の評価
最後に,学習データが300個のとき (初期学習データに160個の学習データを追加したとき) の分類境界を可視化します。能動学習で分類境界に近い学習データから優先して追加していくことで,ランダムに学習データを追加したときよりも正解率の高いモデルを得られたことがわかります。
def plot_predict_results_on_the_query(X, y, experiment_result, query_index, round_index=0, model_def=None):
'''
query_indexで指定したqueryまでに作成した訓練データでモデルを学習し,
そのモデルの分類境界を可視化する関数
'''
# query_indexまでに作成した学習データのインデックスを取得
selected_indices = numpy.array([x['select_index'] for x in experiment_result[round_index]._StateIO__state_list[0:query_index]]).flatten()
# 初期学習データのインデックスを取得
initial_labeled_indices = experiment_result[round_index].init_L
# 学習データ用のインデックスを作成
labeled_indices = numpy.hstack((selected_indices,initial_labeled_indices))
# 学習データの作成
X_train = X[labeled_indices]
y_train = y[labeled_indices]
# モデルの学習
if model_def is None:
model = SVC(probability=True, gamma=0.05, C=1, random_state=2019)
model.fit(X_train, y_train)
# 正解率の計算
pred_test = model.predict(X_test)
accuracy = accuracy_score(y_test, pred_test)
# 分類確率をプロット
plot_predict_results(model, X, y, X_train, accuracy)
print("能動学習した場合")
plot_predict_results_on_the_query(X, y, al.get_experiment_result(), 160, 0)
print("ランダム選択した場合")
plot_predict_results_on_the_query(X, y, al.get_experiment_result(), 160, 5)
能動学習した場合
ランダム選択した場合
まとめ
本記事で示したように能動学習を活用すれば,比較的少ない学習データで精度の良いモデルを学習でき,学習データの作成工数を低減できます。本記事ではSVMとtoy dataで実験を行いましたが,深層学習のように大量の学習データを必要とするアルゴリズムや,医療画像の診断などラベル付けに高度な専門知識が必要になるタスクであれば,能動学習は特に有用な技術となります。
一方,能動学習の課題としては,データ追加を終了するタイミングの判定や,モデル選択との組み合わせが挙げられます。この課題は能動学習が「特定のモデルの高精度化に有用なデータ」から順に追加しますから,実際のデータ分布を反映した有効な評価データを作成できないことに起因します。この点は能動学習の実用上,重要な課題として盛んに研究されておりますのでご興味のある方はぜひ調べてみてください。