データ分析をする人であれば一度は「多重共線性」という言葉を聞いたことがあると思います。色々な人の話を聞いてみると、
- とりあえず知らないとやばいらしい
- 不安定ってなんだよ
- 機械学習だと別に気にしなくてもいいらしい
- 結局よく分からんかった
みたいな感じで、どれを見てもなんか釈然としなくてよく分からないということみたいです。。
というわけで今回は 多重共線性って何が問題なの? というお話をしていきたいと思います。
分析の目的が予測なら気にしなくていい
多重共線性について調べてみると
- 機械学習では気にしなくてよい
- 統計学では気にするべき
というように統計学と機械学習で区別するような説明が一定数出てくるようです。
しかし、これは少し雑なように思います。
多重共線性の問題を考えるときに意識するべきことは、分析の目的が
- 目的変数の予測のみの場合は気にしなくてもよい(たぶん)1
- 目的変数の予測のみではなく 説明にも興味がある場合は気にするべき
というように考えていいかなと思います。
ここで説明といっているのは、説明変数が目的変数に与える影響がどの程度かが論点になる場合のことを指します。
多重共線性とは、説明変数の中に相関係数が非常に高い組み合わせがあること
多重共線性とはざっくり言ってしまえば、説明変数の中に相関係数が非常に高い組み合わせがあること をいいます1
もう少しいうと「ある説明変数」と「他のいくつかの説明変数の和」の相関係数が大きくなる組がある場合も多重共線性に該当します(つまり、$x_1$ と $x_2+x_3$ の相関係数が大きいときも該当します)
※ここでいう相関係数は、ピアソンの積率相関係数を指します。
\rho(X, \ Y) = \frac{\mathrm{E} \left[ \left( X- \mathrm{E} \left[ X \right] \right) \left( Y-\mathrm{E} \left[ Y \right] \right) \right]}{\sqrt{\mathrm{E} \left[ \left( X- \mathrm{E} \left[ X \right] \right)^2 \right] \mathrm{E} \left[ \left( Y- \mathrm{E} \left[ Y \right] \right)^2 \right]}} \tag{1}
ピアソンの積率相関係数は何を表しているかというと、$X$ と $Y$ の線形関係の強さを表しています。
ピアソンの積率相関係数は$X$ と $Y$ が完全な線形関係にあるとき 1 になります。
$X$ と $Y$ に何かしらの関係があっても、線形の関係でなければ1にはならない点には注意が必要です。これに関してはwikipediaに貼ってあった画像がイメージしやすいかと思います。
【参考】散布図と相関係数:wikipediaより拝借

今回の問題の前提:線形モデル(読み飛ばしてOKです)
※一応書いているだけなので、この章は飛ばして読んで大丈夫です。普通の線形モデルを考えるよという話で目新しいことは何も書いていません。
今回は線形モデルにおける多重共線性を扱います。非線形モデルというか機械学習系のモデルでも似たような感じらしいです。あんまり詳しくないので、ざっと調べてふむふむとなったやつを貼っておきます。
線形モデルは、$n$ 組の観測 $ \{ y_i, x_{i1},\cdots, x_{ip} \} , \ i=1,\cdots,n$ の間に
y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i \,\,\,,\,\,\,i=1,\cdots,n \tag{2}
が成り立つことを想定するモデルのことです。$\varepsilon_i$ は誤差項で、
- $\mathrm{E}[\varepsilon_i]=0$
- $\mathrm{V}[\varepsilon_i]=\sigma^2$
- $\mathrm{Cov}(\varepsilon_i,\varepsilon_j)=0 \ \ (i≠j)$
とします。
行列で表現した方が色々と便利なので、行列で表現すると、
Y=X\beta+\varepsilon \tag{3}
となります。
ここで、$Y = (y_1,\ y_2,...,\ y_n)^T$ は目的変数ベクトル、$\beta = (\beta_1,\ \beta_2,...,\ \beta_p)^T$ は係数ベクトル、$\varepsilon = (\varepsilon_1,\ \varepsilon_2,...,\ \varepsilon_n)^T$ は係数ベクトル、$X$ は説明変数の行列で
X = \left(
\begin{array}{cccc}
1 & x_{11} & \cdots & x_{1p}\\\
\vdots & \vdots & \ddots & \vdots \\\
1 & x_{n1} & \cdots & x_{np}
\end{array}
\right) \tag{4}
です($X$ は計画行列とも呼んだりします)
※ちなみに一般的な線形回帰の仮定では、説明変数は確率変数ではありません。固定された既知の定数であると考えます。
▼最小二乗法による解
パラメータ $\beta$ を最小二乗法によって推定すると、
\hat{\beta}=(X^TX)^{-1}X^Ty \tag{7}
が求まります。これをOLS推定量(Ordinary Least Squares Estimator)と呼びます。
多重共線性の問題は分析が不安定になること?
◆ざっくりとした結論
結論を言ってしまうと、 多重共線性があると回帰係数の推定量の分散が大きくなる ということが問題になります。
それ以外はたぶんないです。たぶん。
(もしあったら教えてください・・)
また、よくいわれる「分析が不安定になる」とは、回帰係数の推定量の分散が大きくなることを指しています。
回帰係数の推定量の分散が大きくなるということは、一回一回の推定における値のぶれが大きくなってしまうということです。
実務の場では、データを無限個とったり、データを何回も取り直して同じ分析をやったりというリッチなことはできないので、この一回一回の推定のぶれが大きくなることは結構深刻な問題になります。
◆数式で考えてみる
多重共線性が引き起こす問題について、数式をガチャガチャして考えてみます。
ここでは2つのパターンについて考えます。
- 完全に比例した関係の説明変数の組がある場合
- 相関係数が非常に高い組み合わせがある場合
これらについて考えていきます。
① 完全に比例した関係の説明変数の組がある場合
例えば、2つ目の説明変数 $x_2$ が1つ目の説明変数 $x_1$ の定数倍になっている状況です。
なので、$x_2 = ax_1, a \in \mathbb{R}$ になっている状況、すなわちデータが
X = \left(
\begin{array}{cccc}
1 & x_{11} & \color{red}{ax_{11}} & \cdots & x_{1p}\\\
\vdots & \vdots & \color{red}{\vdots} & \ddots & \vdots \\\
1 & x_{n1} & \color{red}{ax_{n1}} & \cdots & x_{np}
\end{array}
\right) \tag{8}
というときにどうなるか考えてみます。
結論としては、そもそも回帰係数 $\hat{\beta}=(X^TX)^{-1}X^Ty$ が求まりません。
$X^TX$ の逆行列 $(X^TX)^{-1}$ が求められないからです。
逆行列が求められない条件などについては、こちらを参照するとわかりやすいかなと思います。
ざっくり教科書を思い出してみると、正方行列 $A$ の余因子行列を $\tilde{A}$ とすると、行列 $A$ の逆行列 $A^{-1}$ は、
A^{-1} = \frac{1}{|A|} \tilde{A} \tag{9}
です。当然、行列式 $|A|$ が $0$ になってしまうと $A^{-1}$ は求まりません。
では、行列式 $|A|$ がどのようなときに 0 になってしまうかというと、$A$ が以下のどれかに該当すると 0 になってしまいます。
1. 1つの列成分がすべて0
2. 2つの列が等しい
3. 2つの列が比例している
$X$ に完全に比例した関係の説明変数の組があると、$X^TX$ に関して 3 に該当してしまい $(X^TX)^{-1}$ が求められないという状況になってしまうというわけです。
(補足)
$X$ に多重共線性があるのと $X^TX$ に多重共線性があるかは別では?という質問を受けたことがあるので補足です。
仰る通りなのですが、計算してみると $X$ に多重共線性があれば $X^TX$ にも多重共線性があるということが分かります。
簡単のため説明変数が3つで、3つ目が2つ目に比例している場合を考えます。
すなわち $X = (x_1 \ x_2 \ \alpha x_2)$ のときです。
このとき $X^TX$ は、
\begin{eqnarray}
X^TX &=& \left(
\begin{array}{cccc}
x_1^T x_1 & x_1^T x_2 & \alpha x_1^T x_2 \\\
x_2^T x_1 & x_2^T x_2 & \alpha x_2^T x_2 \\\
\alpha x_2^T x_1 & \alpha x_2^T x_2 & \alpha^2 x_2^T x_2 \\\
\end{array}
\right) \tag{10} \\
&=& \left(
\begin{array}{cccc}
x_1^T x_1 & x_1^T x_2 & \alpha (x_1^T x_2) \\\
x_2^T x_1 & x_2^T x_2 & \alpha (x_2^T x_2) \\\
\alpha x_2^T x_1 & \alpha x_2^T x_2 & \alpha (\alpha x_2^T x_2) \\\
\end{array}
\right) \tag{11}
\end{eqnarray}
となり、3列目が2列目に比例している形になっていることが分かります。
簡単ですが意外とこの部分の計算を追ったことがない人はいるみたいなので、ぜひ一度手を動かしてみると良いかなと思います。
ここまでをまとめると、完全に比例した関係の説明変数の組がある場合、
- $X^TX$ が3の状況に該当 → $|X^TX|=0$ → $X^TX$の逆行列が求まらない
という流れで、そもそも回帰係数 $\hat{\beta}=(X^TX)^{-1}X^Ty$ が求まらない
ということが分かりました。
(ちなみに逆行列を求められる行列を正則行列といいます。Ridgeをはじめとする手法が "正則化" と呼ばれているのは、正則ではない行列を正則な行列にするという発想からきています。)
② 相関係数が非常に高い組み合わせがある場合
実際のデータ分析では、完全に比例しているデータに出くわすことはまずないので、こちらが考えるべき主な問題となります。
▼ 回帰係数の分散を計算してみる
回帰係数の分散を求めてみます。
{\begin{eqnarray}
\mathrm{V}[\, \hat{\beta}\,] &=& \mathrm{V}\biggl[\, (X^TX)^{-1} X^T y\, \biggr] \\
\\
&=& (X^TX)^{-1} X^T \mathrm{V}\,[\,y\,] X(X^TX)^{-1} \\
\\
&=& (X^TX)^{-1} X^T (\sigma^2 I) X(X^TX)^{-1} \\
\\
&=& \sigma^2 \underbrace{(X^TX)^{-1} X^TX}_{I}(X^TX)^{-1} \\
\\
&=& \sigma^2 (X^TX)^{-1} \tag{12}
\end{eqnarray}
}
というわけで、$\hat{\beta_j}$ の分散は、
\mathrm{V}[\, \hat{\beta_j} \, ] = \sigma^2 (X^TX)^{-1} の \ (j,j) \ 要素 \tag{13}
と求まりました。
これをもとに説明変数どうしに相関がある場合の表現を計算します。
と思ったのですが、、、
線形モデルの説明変数の数が2の場合はともかく、一般の場合は思ってたよりも難しくて計算過程がよく分からなかったので後日の宿題ということで・・(調べても2変数の場合しか出てこないし・・)
まあでも結論は次の形になるようです。
\mathrm{V}[\ \hat{\beta}_j^* \ ] = \sigma^2 \frac{1}{\mathrm{V}[X_j]} \frac{1}{1-R^2_j} \tag{14}
ここで $R^2_j$ は、$X_j$ を目的変数にし $X_j$ 以外の説明変数で回帰したときの決定係数です。
($\hat{\beta}_j^*$ は説明変数どうしが相関している場合の$j$番目の回帰係数の推定量)
$(14)$ 式の意味を考えてみます。
$X_j$ を $X_j$ 以外の説明変数で回帰したときの決定係数 $R^2_j$ が 1 に近いということは、 $X_j$ は $X_j$ 以外の説明変数と線形の関係にあるということです(多重共線性がある)。
$R^2_j$ が 1 に近付くにつれて $\frac{1}{1-R^2_j}$ は $0$ に近付くので、結果として回帰係数の分散 $\mathrm{V}[\hat{\beta}_j^*]$ もどんどん大きくなっていくことが分かります。
つまり、多重共線性があると、回帰係数の分散も大きくなるということを意味しています。
また $(14)$ 式の $\frac{1}{1-R^2_j}$ 部分を $x_j$ の $\mathrm{VIF}$(Variance Inflation Factor:分散拡大係数)といいます。
\mathrm{VIF}_j = \frac{1}{1-R^2_j} \tag{15}
いつもなんとなく使っている VIF はこんな発想からきていたんですね。まじ賢い。
ここまでをまとめると、
相関係数が高い説明変数の組があると、その回帰係数のVIFが大きくなる。そしてVIFが大きくなると回帰係数の分散もどんどん大きくなってしまう
ということが分かりました。
これがいわゆる分析が不安定になるというやつです。
※説明変数どうしに相関がある場合の回帰係数の分散について、唯一計算過程が書いてあったのを見つけたこの記事を参考までに・・
(ちなみに)VIFと信頼区間の関係
ちなみに $j$ 番目の回帰係数の信頼区間の幅 $\mathrm{VLC}_j$ は、
\mathrm{LCI}_j = 2 × t_{\frac{\alpha}{2}, \ {n-(p+1)}} \hat{\sigma} \, \mathrm{SE} \left[ \hat{\beta}_j \right] \tag{16}
と書けます。
(14) (15) から説明変数どうしに相関がある場合の $\mathrm{SE} [\beta_j^*]$ は、相関がない場合を $\mathrm{SE}[\beta_j]$ とすると
{\begin{eqnarray}
\mathrm{SE} [\beta_j^*] &=&\sqrt{\mathrm{V} \ [\beta_j^* ]}
\\\\
&=& \sqrt{\sigma^2 \frac{1}{\mathrm{V}[X_j]} \frac{1}{1-R^2_j}}
\\\\
&=& \sqrt{\sigma^2 \frac{1}{\mathrm{V}[X_j]} \mathrm{VIF}_j}
\\\\
&=& \mathrm{SE}\left[\beta_j\right] \sqrt{\mathrm{VIF}_j} \tag{17}
\end{eqnarray}}
となるので、多重共線性が生じている場合の $j$ 番目の回帰係数の信頼区間の幅 $\mathrm{VLC}_j$ は、(16)(17) より、
{\begin{eqnarray}
\mathrm{LCI}^*_j &=& 2 × t_{\frac{\alpha}{2}, \ {n-(p+1)}} \hat{\sigma} \, \mathrm{SE} \left[ \hat{\beta}_j \right] \sqrt{VIF_j} \tag{18}
\\\\
&=& \mathrm{LCI}_j \ \sqrt{\mathrm{VIF}_j} \tag{19}
\end{eqnarray}}
と書けるので、多重共線性が生じていない場合と比べて $\sqrt{\mathrm{VIF}_j}$ 倍だけ広くなることが分かります。
つまり、$\mathrm{VIF}$ は信頼区間の幅がどれだけ広くなってしまうかの指標にもなっているというわけです。
シミュレーション
実際問題、多重共線性があると分析結果はどんな感じになるのか、シミュレーションで確かめてみます。
神のみぞ知る真のモデルは下記で設定します。
真のモデル:
y = 3 + 5X_1 + 10X_2 + 20X_3 + ε, \ \ \varepsilon \sim N(0 ,\ 5^2) \tag{20}
シミュレーションは、下記設定で行います。
-
データ:$x_1$ と $x_2$ に相関がある場合を考える
-
使用するモデル:
1. 全ての説明変数を使う
2. $x_2$ を使わない
3. $x_1$ と $x_2$ を合算した説明変数 $x_1+x_2$ を使う
4.PCR(主成分回帰)
5.PLS(部分的最小二乗回帰)
6.Ridge回帰
7.Lasso回帰
※書いていて疲れちゃったので、4~7はまた今度で・・
それぞれ下記5つを調べます。
- 相関係数ごとの回帰係数の分散(各1,000回推定の分散)← 不安定さ
- 相関係数ごとの回帰係数の平均(各1,000回推定の平均)← 不偏性
回帰係数に関するMSE(真の値に対する各1,000回推定の平均)目的変数に関するMSE(未知データに対するに対する1,000回推定の平均)- 相関係数が大きいとき(0.9のとき)にサンプルサイズを増やすと推定値はどうなるか(最大サンプルサイズ50,000)← 一致性
※実験し忘れちゃったので、3と4はまた今度で・・
1. 全ての説明変数を使う
まずは、全ての説明変数を使うパターンです。
推定に用いるモデルは、
f(X) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 \tag{17}
です。
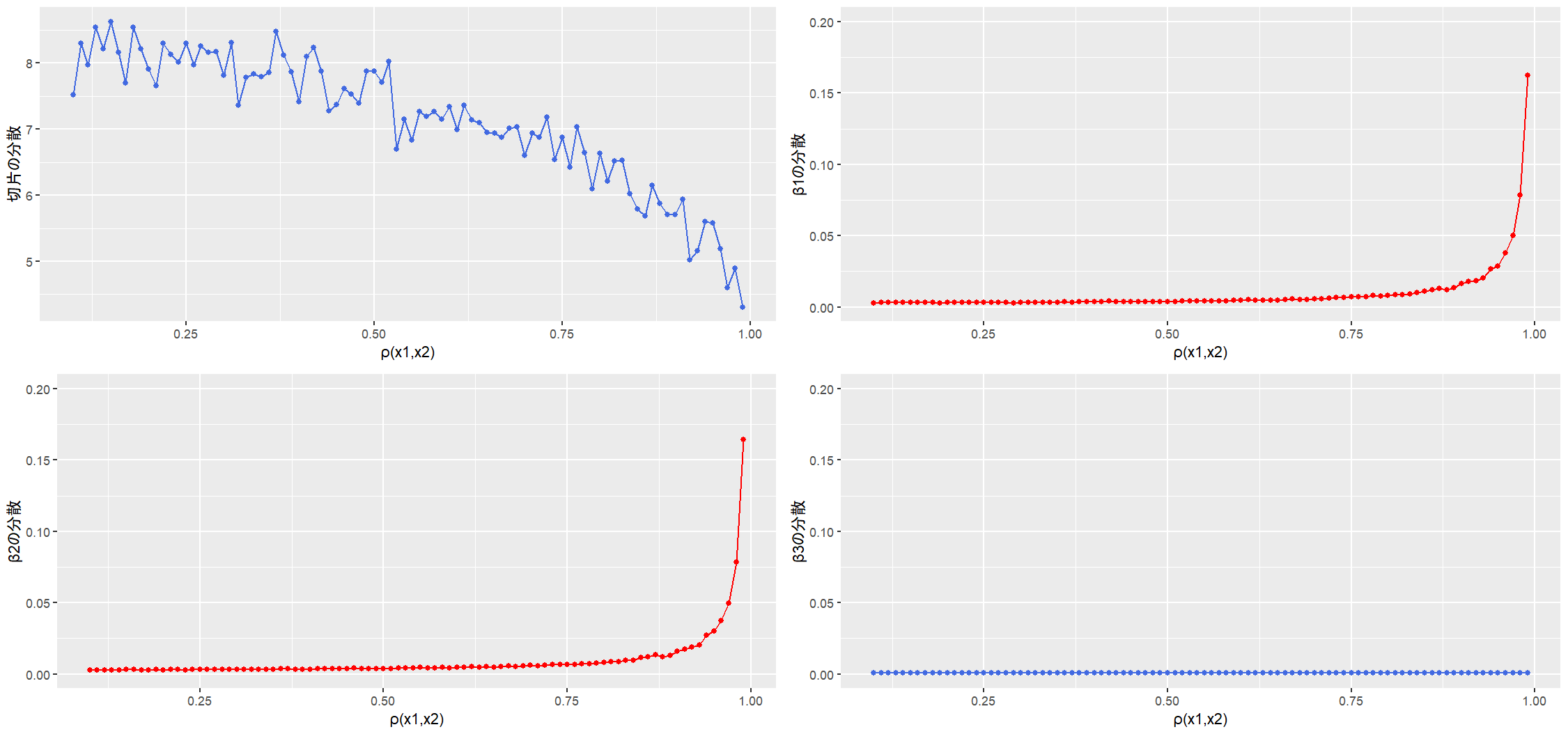
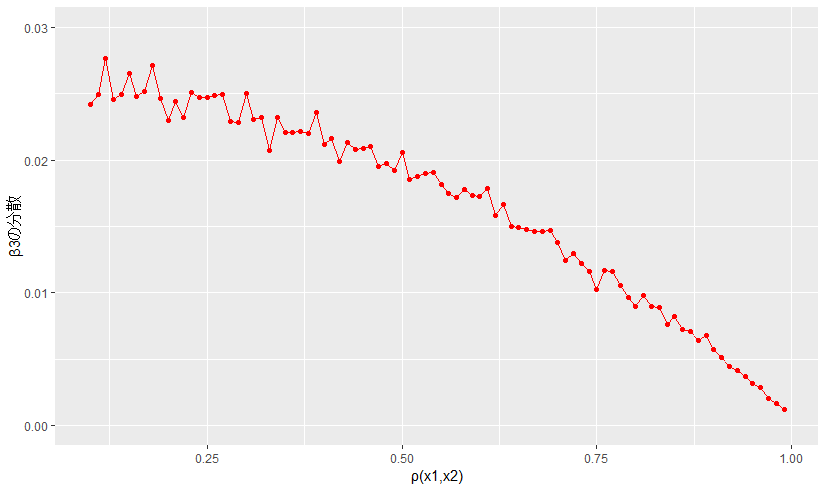
1-1. 相関係数ごとの回帰係数の分散(不安定さの確認)
$X_1$ と $X_2$ に相関があるので、$(14)$ 式の通りであれば $X_1, X_2$ に対応する回帰係数の分散 $V[\hat{\beta_1}]$ と $V[\hat{\beta_2}]$ が大きくなり、 $V[\hat{\beta_0}]$ と $V[\hat{\beta_3}]$ は相関係数の影響を受けないと思われます。
(スクロール面倒だと思うので$(14)$式再掲:回帰係数 $\beta_j$ の分散)
\mathrm{V} \ [\, \hat{\beta}_j^* \, ] = \sigma^2 \frac{1}{\mathrm{V}[X_j]} \frac{1}{1-R^2_j} \tag{14}
※$R^2_j$ は、$X_j$ を目的変数にし $X_j$ 以外の説明変数で回帰したときの決定係数
結果は次のようになりました。
- 横軸:$X_1$ と $X_2$ の相関係数 $\rho(X_1, X_2)$
- 縦軸:相関係数ごとの回帰係数の分散
期待通り $\rho(X_1, X_2)$ が大きくなるにつれて、$\mathrm{V} [\hat{\beta_1}]$ と $\mathrm{V} [\hat{\beta_2}]$ が大きくなっています。
$X_3$ と相関が高い説明変数はないので、$\mathrm{V} [\hat{\beta_3}]$ は $\rho(X_1, X_2)$ の影響を受けておらず、推定は安定しているといえます(切片の分散が小さくなっていっているのはちょっと気になるかも・・)
ちなみに $\rho(X_1, X_2)$ が $0$ のときと $0.9$ のときで、各回帰係数の推定値の分布を書いてみるとこんな感じです。
$\rho(X_1, X_2) = 0.9$ のときは、それに対応する回帰係数 $\hat{\beta_1}$ と $\hat{\beta_2}$ の分布が広がっている様子が見て取れます。
ということで、
説明変数の中に相関係数が高い組があると、それに対応する回帰係数の分散が不安定になる(分散が大きくなる)
ことが分かりました。
ちなみにちなみに、$\hat{\beta_1} + \hat{\beta_2}$ の分布に関して $\rho(X_1, X_2)$ が $0$ と $0.9$ の時で比較すると次のようになります。
相関係数の大小によらず、$\hat{\beta_1}+\hat{\beta_2}$ の分布はあまり変わらないようです(むしろ相関係数が高い方がばらつきが小さくなっている気がする)赤線は $\beta_1$ と $\beta_2$ の真の値の合計で、この値の周りに分布している様子が見て取れます。
相関がある説明変数に対応する回帰係数は互いに食い合っているだけで、これら回帰係数の合計は安定していそうです。
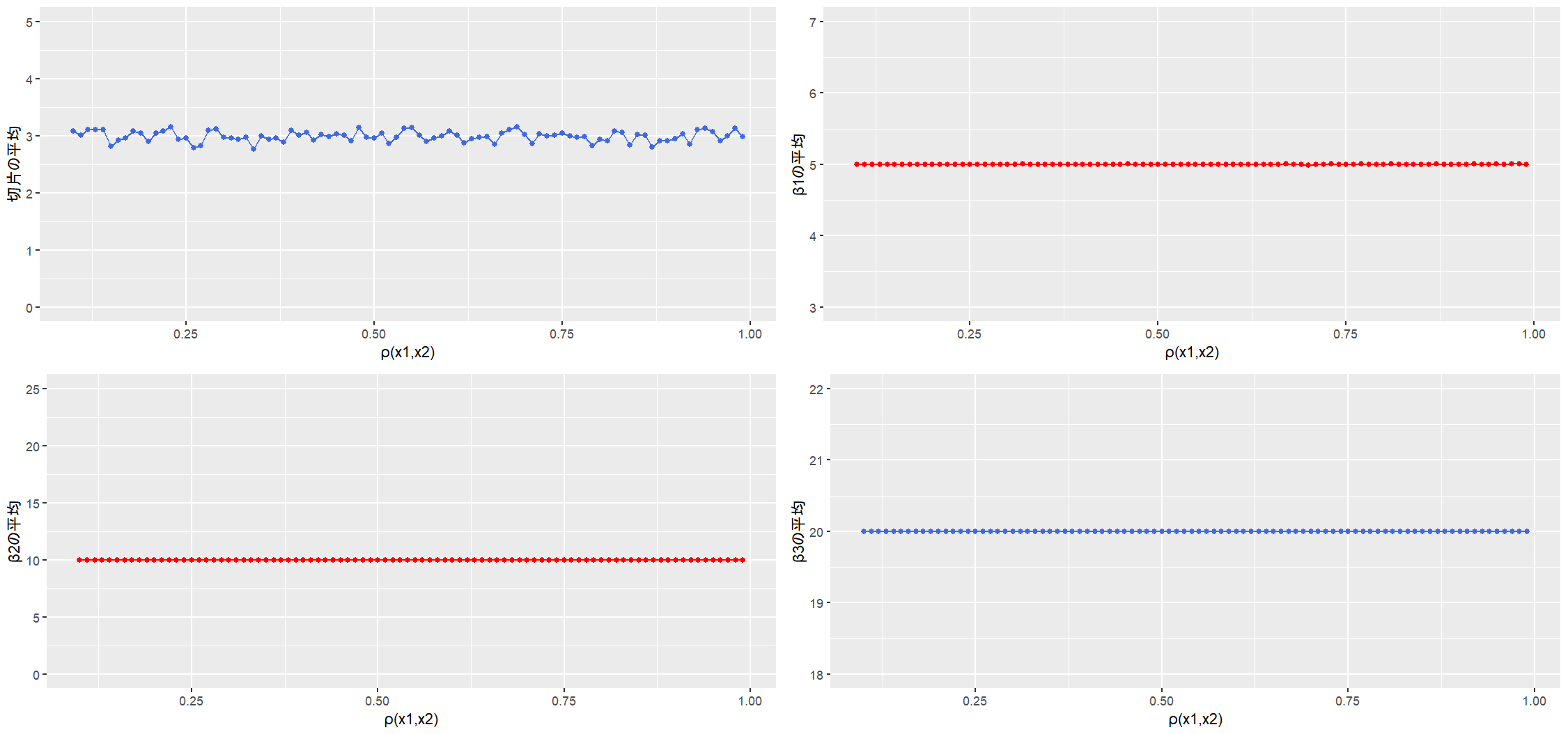
1-2. 相関係数ごとの平均的な回帰係数の推定値(不偏性の確認)
相関係数ごとの回帰係数の推定値の平均を計算します(つまり不偏性を確認したい)
- 縦軸:相関係数ごとの回帰係数1,000回推定の平均
- 横軸:$X_1$ と $X_2$ の相関係数 $\rho(X_1, X_2)$
回帰係数の平均値は相関係数の影響を受けない ようです。
切片がジグザグしていますが縦軸の問題な気もするので一旦おいておきます。
この結果には意外という気持ちを持った人もいるかもしれませんが、これは OLS推定量の不偏性 によるものなので、当然と言えば当然の結果といえます。
つまり、データを何回も何回も取得できて分析を何回も実行できるプロジェクトにおいては、多重共線性とか気にせずに複数回分析した結果を平均してやればいいわけです。
そんなリッチなプロジェクトは中々存在しないと思いますが・・
まとめると、 多重共線性の問題を抱えていても、OLS推定量は平均的に正しい推定を行う ということが分かりました。
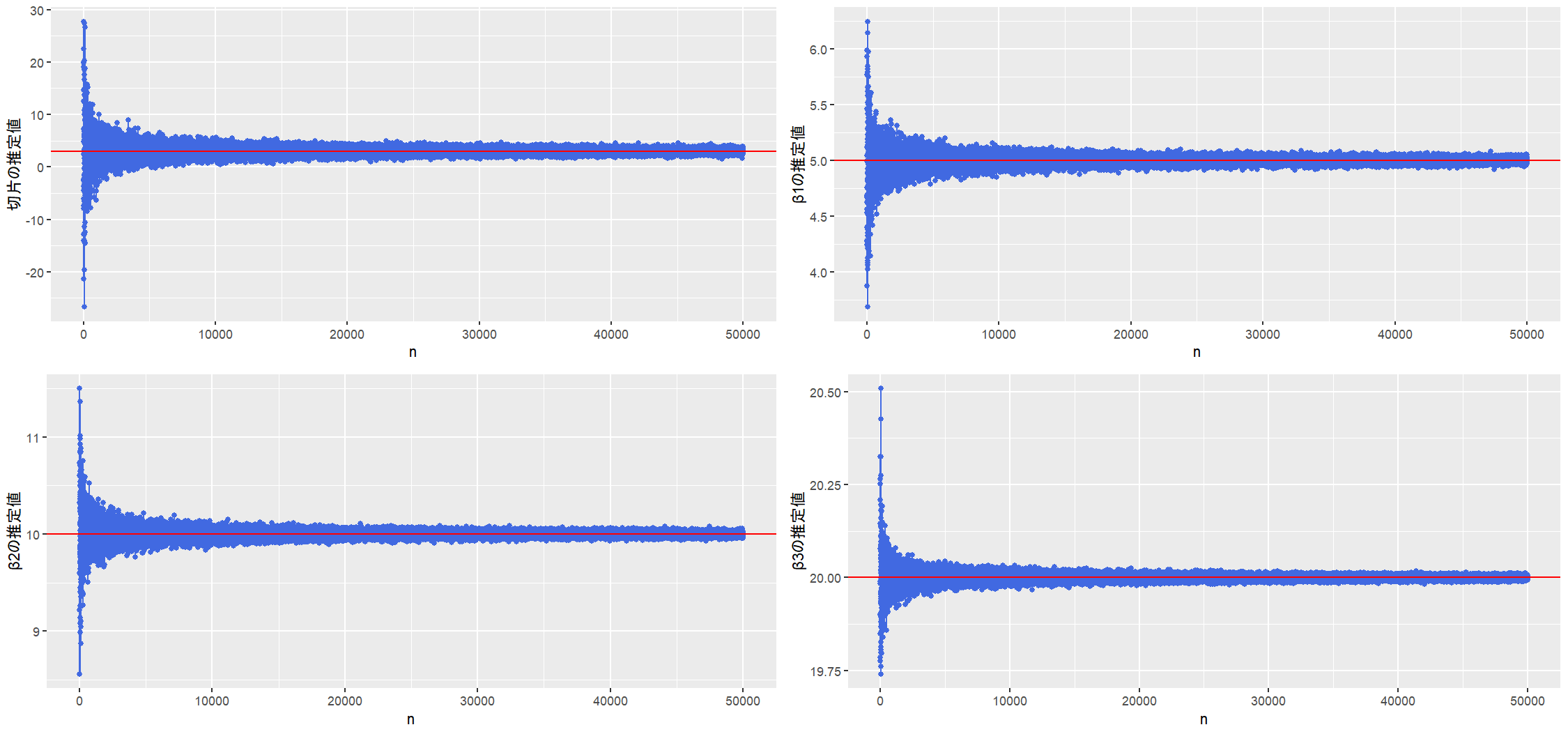
1-3. 相関係数が大きいときにサンプルサイズを増やすと推定値はどう変化するか(一致性の確認)
相関係数が0.9のときにサンプルサイズを増やしていくと回帰係数の推定値がどうなるのかを調べます(つまり一致性を確認したい)
- 縦軸:サンプルサイズごとの回帰係数1回推定の値
- 横軸:$X_1$ と $X_2$ の相関係数 $\rho(X_1, X_2)$
サンプルサイズが大きくなるほど、回帰係数の推定値は収束しているように見えます。
これも当然と言えば当然の結果で、 OLS推定量の一致性 によるものです。
ということで、多重共線性の問題はサンプルサイズを大きくすることで解決する ということが分かりました。
★X1とX2に相関がある場合のまとめ
この実験で分かったことをまとめます。
説明変数の中に相関が高い組み合わせがある場合、下記のことが分かりました。
- 相関係数が高い説明変数に対応する回帰係数の分散が大きくなる
- 相関が高い説明変数に対応する回帰係数の推定値の合計は分散が大きくならない
- 相関の高い相手がいない説明変数の回帰係数の推定は分散が大きくならない
- 回帰係数の平均を考える場合は、説明変数間に高い相関を持つものがあっても問題ない(不偏性)
- 多重共線性の問題は、サンプルサイズを大きくすると解決する(一致性)
2. X1とX2に相関があり、推定モデルにはX1のみを使う場合
巷では、相関係数が高い説明変数がある場合、片方だけ使うことが推奨される場合がしばしばあるようです。この対応が正しいのか調べてみます。
推定に用いるモデルは、
f(X) = \beta_0 + \beta_1 X_1 + \beta_3 X_3 \tag{18}
です。
2-1. 相関係数ごとの回帰係数の分散(不安定さの確認)
早速結果です。
$\rho(X_1, X_2)$ が大きくなればなるほど、$V[\hat{\beta_1}]$ が小さくなっていく様子が伺えます。
これは $\rho(X_1, X_2)$ が大きくなるほど、
\begin{eqnarray}
y &=& 3 + 5X_1 + 10 \underbrace{X_2}_{→ \ X_1} + 20 X_3 + \varepsilon \tag{16} \\
\\
&≒& 3 + (5 + 10) X_1 + 20 X_3 + \varepsilon \tag{19}
\end{eqnarray}
という形になり2、結果として $f(X) = \beta_0 + \beta_1 X_1 + \beta_3 X_3$ で予測しても、不安定さの観点では問題なくなったんじゃないかなと思われます。
一方で、また$\mathrm{V}[\hat{\beta_0}]$ も $\rho(X_1, X_2)$ が大きくなるほど小さくなっています。
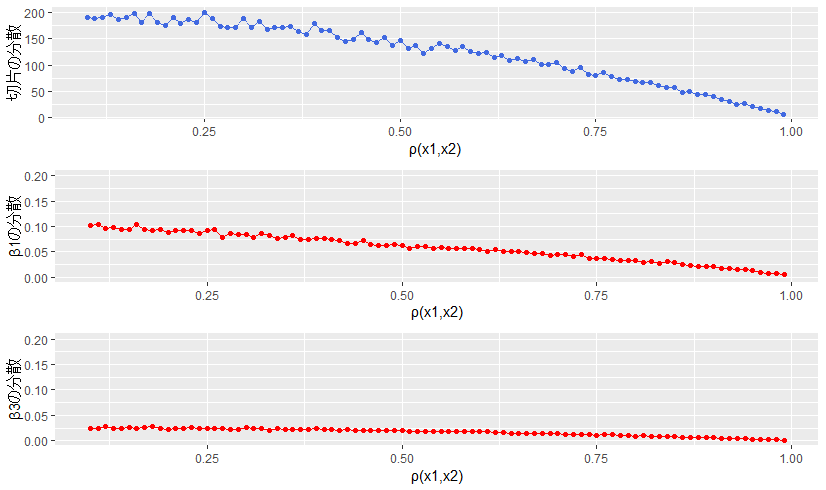
また、$\mathrm{V}[\hat{\beta_3}]$ は $\rho(X_1, X_2)$ によらず小さいです。でも目を細めてよく見ると微妙に下がっていっているようにも見えます。$\mathrm{V}[\hat{\beta_3}]$ に関して拡大した図をかいてみると、
目を細めて見た感覚はあってるっぽいですね。やっぱり $\rho(X_1, X_2)$ が大きくなると、$\mathrm{V}[\hat{\beta_3}]$ は小さくなっていくようです。
これは $\rho(X_1, X_2)$ が小さいときには欠落変数の問題が生じているせいで、分散が大きくなってしまっているということが起こっているためかなと思います。
$\rho(X_1, X_2)$ が大きくなると、上に述べたように式 $(19)$ を式 $(18)$ 式で推定するような形になるので、欠落変数の問題は隠されてしまうという形になるんだと思います3
ということで、
多重共線性の問題がある場合にどちらか一方の説明変数を用いることは、分析の不安定さ(推定値の分散)という観点ではまあ問題なさそう
だということが分かりました(切片の分散を考える場合は問題ありそうではあります)
2-2. 相関係数ごとの平均的な回帰係数の推定値(不偏性の確認)
これも早速結果を。
黒線で真の値を入れてみました。
$\hat{\beta_1}$ はバイアスを持っており、不偏推定量になっていないことが分かります。
これもやはり欠落変数バイアスによるものだと考えられます。
$X_2$ を落とした場合の $\hat{\beta_1}$ の期待値は、
\mathrm{E}[\hat{\beta_1}] = \beta_1+\beta_2 \frac{\mathrm{Cov}[X_1, X_2]}{\mathrm{V}[X_1]}
であり、相関が大きいほど(共分散が大きいほど)バイアスも大きくなることが分かります。
また、$\rho(X_1, X_2)$ が大きくなるにつれて、切片は真の値に近付いていき、$X_1$ は $X_2$ の影響を吸い取っていく様子が分かります($\mathrm{E}[\hat{\beta_1}]$ が $\beta_1 + \beta_2$ に近付いていく)
これはやはり、 $\rho(X_1, X_2)$ が大きくなるにつれて、式 $(19)$ を式 $(18)$ で回帰している状況に近くなるからだと思われます。
また、意外にもこのシミュレーションの結果を見る限りで $\hat{\beta_3}$ は不偏推定量になっているように見えます。これはおそらく $X_3$ と欠落変数である $X_2$ が独立になっているため、欠落変数バイアスが乗ってこないからだと思います。
ということで、多重共線性の問題がある場合にどちらか一方の説明変数を用いることは、平均的な推定という意味で多重共線性の問題である「説明」の観点では問題を解決していることにはならないということが分かりました($X_1$の回帰係数$\hat{\beta_1}$は$\beta_1$を正しく推定しない)
2-3. 相関係数が大きいときにサンプルサイズを増やすと推定値はどう変化するか(一致性の確認)
これも1と同じように相関係数が0.9で設定します。
それでは結果です。
赤線は真の値です。
切片と $\beta_1$ は、サンプルサイズが大きくなると収束してはいますが、真の値に収束することはないようです。一方で $\beta_3$ は真の値に収束しているように見えます。
ということで、多重共線性が発生しているときにどちらか一方の説明変数を使用するという方法をとっている場合、サンプルサイズを大きくしても推定値は真の値を予測できないということが分かりました。
つまり、この場合も多重共線性の問題である説明の観点では問題を解決していることにはならないということです。
★X1とX2に相関がある場合、説明変数にX1のみを使う場合のまとめ
この実験で分かったことをまとめます。
説明変数の中に相関が高い組み合わせがあり、説明変数にX1のみを使う場合、下記のことが分かりました。
- 分析の不安定さ(推定値の分散)という観点ではまあ問題なさそう
- 平均的な推定という意味で、多重共線性の問題である「説明」の観点では問題を解決しない(不偏性はない)
- サンプルサイズを大きくしても、多重共線性の問題である「説明」の観点では問題を解決しない(一致性はない)
3. X1とX2に相関があり、推定モデルにはX1とX2を合算した説明変数(X1+X2)を使う場合
せっかくもっているデータを捨ててしまうのはなんだかもったいない気がするので、相関係数が高い者どうしを合計し、新たな特徴量として使う場合について考えてみます。
推定に用いるモデルは、
f(X) = \beta_0 + \beta_{12} (X_1 + X_2) + \beta_3 X_3 \tag{20}
です。
3-1. 相関係数ごとの回帰係数の分散(不安定さの確認)
早速結果です。
切片以外の分散は $\rho(X_1, X_2)$ によらず小さく抑えられているようなので、$X_1, \ X_2$ の代わりに $X_1+X_2$ という新しい特徴量を使うことは、分析の不安定さという観点では問題なさそうです。
ちなみにですが、$V[\beta_{12}]$ も $V[\beta_3]$ も拡大して見てみると $\rho(X_1, X_2)$ が大きくなるにつれて小さくなっています。
ということで、$X_1$ と $X_2$ に相関がある場合、推定モデルに $X_1, \ X_2$ の代わりに $X_1+X_2$ を使うことは、分析の不安定さという観点で問題なさそうだということが分かりました。
3-2. 相関係数ごとの平均的な回帰係数の推定値(不偏性の確認)
これも早速結果を。
切片と $\beta_3$ の推定値は、真の値をとらえているようです。
一方で、$\beta_{12}$ の推定値の平均はおよそ7.5になっており、これは $\beta_1$ と $\beta_2$ の真の値である 5 と 10 の平均になっています((5+10)/2=7.5)
ということで、$X_1$ と $X_2$ に相関がある場合、推定モデルに $X_1, \ X_2$ の代わりに $X_1+X_2$ を使うと、平均的に、切片と $\beta_3$ には真の値を推定し、$X_1 + X_2$ の回帰係数 $\beta_{12}$ に関しては、もともとのそれぞれの係数係数 $\beta_1$ と $\beta_2$ の平均を推定するということが分かりました(今回の実験では平均になりましたが、これは下の※に書いたように平均を推定しているのではなく、説明変数の分散に依存した値を推定します)
※余談:説明変数を合計した場合のOLS推定量※
今回の設定では$\beta_12$の推定値が単に $\beta_1$ と $\beta_2$ の平均になっていましたが、それは観測した $x_1$ と $x_2$ の分散が同じだったためです。
実際、誤特定モデルにおけるOLS推定量は以下のようになります。
\beta_{12} = \frac{\mathrm{Cov}[y, x_1+x_2]}{\mathrm{V}[x_1+x_2]} \tag{21}
この値は分散の大きい方に引っ張られることになります。
これはフィッシャー情報量を考えても自然なことだと思います。
$\beta_{12}$に関するフィッシャー情報量は、
I(\beta_{12}) = \frac{\mathrm{V}[x_1+x_2]}{\sigma^2} \tag{22}
なので、$\beta_{12}$ を推定するうえでは、ばらつきが大きい説明変数の方がより大きな情報を持つということなのだと思います。
※話を単純にしてしまいましたが、式(21)を展開すると式の形から実際は分散共分散構造が大きい方の情報を重視するというようになると思います。
\beta_{12} = \frac{a\,\mathrm{V}[x_1]+b\,\mathrm{V}[x_2]+(a+b)\,\mathrm{Cov}[x_1,x_2]}
{\mathrm{V}[x_1]+\mathrm{V}[x_2]+2\,\mathrm{Cov}[x_1,x_2]} \tag{23}
(疲れてきて日本語がぐちゃってきた・・)
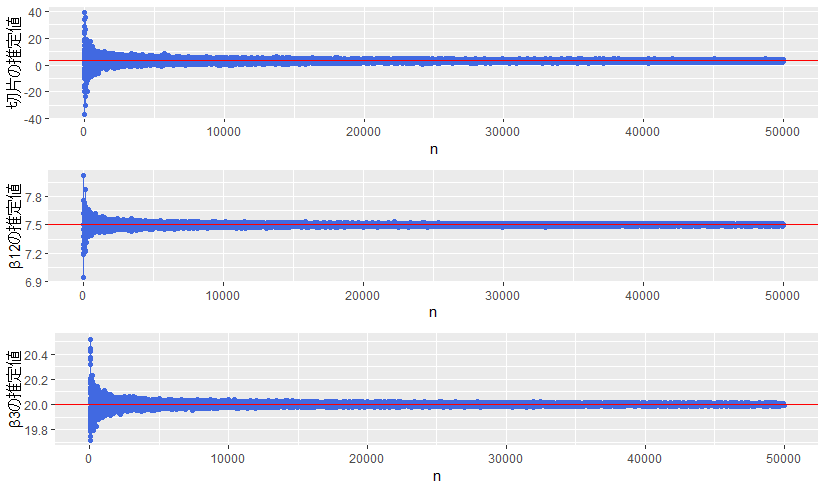
3-3. 相関係数が大きいときにサンプルサイズを増やすと推定値はどう変化するか(一致性の確認)
一致性に関するシミュレーションです。
赤線に関しては、切片と $\beta_3$ は真の値、$\beta_{12}$ は見ての通り、不偏性を調べたときと同じくおよそ7.5になっています。やはりこれは $\beta_1$ と $\beta_2$ の真の値である 5 と 10 の平均になっています((5+10)/2=7.5)
ということで、$X_1$ と $X_2$ に相関があるときに、推定モデルに $X_1, \ X_2$ の代わりに $X_1+X_2$ を使う場合、サンプルサイズを大きくすると、切片と $\beta_3$ は真の値に収束し、$X_1 + X_2$ の回帰係数 $\beta_{12}$ は、もともとのそれぞれの係数 $\beta_1$ と $\beta_2$ の平均に収束することが分かりました。
シミュレーションのまとめ
1.説明変数が過不足なく使われている場合
- 相関係数が高い説明変数に対応する回帰係数の分散が大きくなる(これが不安定になると呼ばれているもの)
- 相関が高い説明変数に対応する回帰係数の推定値の合計は分散が大きくならない
- 相関の高い相手がいない説明変数の回帰係数の推定は分散が大きくならない
- 回帰係数の平均を考える場合は、説明変数間に高い相関を持つものがあっても問題ない(不偏性)
- 多重共線性の問題は、サンプルサイズを大きくすると解決する(一致性)
2.相関係数が高いもののうち、どちらか一方だけを使った場合
- 分析の不安定さ(推定値の分散)という観点ではまあ問題ない
- 平均的な推定という意味で、多重共線性の問題である「説明」の観点では問題を解決しない
- サンプルサイズを大きくしても、多重共線性の問題である「説明」の観点では問題を解決しない
相関係数が高い変数を合計した変数を使う場合
- 分析の不安定さ(推定値の分散)という観点ではまあ問題ない
- 回帰係数は、説明変数の分散共分散構造に依存する
- 推定値の平均値は相関の度合いによらず安定している
- サンプルサイズが大きいときも相関の度合いによらず安定している
参考文献
- 吉田光雄(1987):重回帰分析における多重共線性とRidge回帰について
- 京都大学 平成29年度 中級計量経済学 講義ノート 2: 線形回帰モデル
- 宮岡, 野田:数理統計学の基礎(1992)
- 高橋, 渡辺:欠測データ処理(2017)
- 矢島, 廣津, 藤野, 竹村, 竹内, 縄田, 松原, 伏見:自然科学の統計学(2016)
- 高橋:統計的因果推論の理論と実装(2022)
- 安井:効果検証入門(2020)
-
係数分散の増大は、外挿予測・将来データに対する予測分散を悪化させることに繋がります。特に①サンプルサイズが小さい②学習データと予測対象の分布がずれる場合には予測誤差(MSE)が悪化するので問題がないわけではありません・・ ↩ ↩2
-
比例するといえば $X_2$ は $X_1$ の何倍になっているんだよっていうことを考えるのが筋かもしれませんが、いったん $a=1$ で考えています。$X_2$ が $a$ 倍になると回帰係数は $\frac{1}{a}$ になるので、今回考えている内容に対しては特に問題ないと思っています。 ↩
-
これは欠落変数の議論の枠組みでも考えることができるように思いますの補足(自信ないけど)$Y = X \beta + Z \gamma + \varepsilon$ が真のモデルで $Z$ が欠落変数だとすると、OLS推定量は $\hat{\beta} = (X^T X)^{-1}X^TY = (X^T X)^{-1}X^T(X \beta + Z \gamma + \varepsilon) = \beta + (X^T X)^{-1}X^TZ\gamma + (X^T X)^{-1}X^T\varepsilon$ になります。これの期待値を考えると $E[\hat{\beta}] = \beta + (X^T X)^{-1}X^TZ\gamma$ で $(X^T X)^{-1}X^TZ\gamma$ だけバイアスが乗っていることが分かります。そしてこの $(X^T X)^{-1}X^TZ\gamma$ は式の形から $Z$ を $X$ で回帰したときの回帰係数になっていることが分かります(OLS推定量の$Y$が$Z$になって係数倍されているだけ)$X$と$Z$の相関係数が1で比例定数が1のときには、$X=Z$ となるので結果的に$E[\hat{\beta}] = \beta + \gamma$ と欠落変数の係数分バイアスになるという具合です。 ↩