Go to Qiita Advent Calendar 2024 Top
LoginSignup
27
22

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@MandT500(M&T 500)

日経225全銘柄の投資効率を検証

Last updated at Posted at 2020-12-02

株式投資で資産運用をするとき，
できるだけ少ない資金で，できるだけ小さいリスクで，利益を出していきたいと投資の効率性を考えます．

投資の効率性はリターンとリスクによって決定されます．
したがって，効率的な投資戦略を考えるうえで，重要となるのは，
投資によるリターン（株価収益率），**投資に伴うリスク（収益率の分散）**の理解と
**リスクに見合うリターン（シャープ・レシオ）**が得られているかです．

どの指標も高校数学までのレベルで，数理ファイナンスの世界では基礎的なものです．

本記事では，この3つの指標について理解し，日経225全銘柄について，投資の効率性を検証しました．

投資によるリターン（株価収益率）

まずはじめに，収益の効率を考えるうえで重要となるのは，投資金額に対する収益額の割合（収益率）です．

例えば，1株100円の株券Aを1株購入し，翌日に150円になったときに売却すれば，50円の収益を得ることができます．一方，1株1000円の株券Bを1株購入し，翌日に1050円になったときに売却すれば，株券Aと同じ1株当たり，50円の収益を得ることができます．

1株あたりの収益額でみると，どちらも同じ利益を得ています．一方で，収益の効率を考えたとき，株券Aでは100円を投資して，50円の利益を得られているのに対して，株券Bでは1000円も投資したのに50円の利益しかえられていません．1000円もあれば，株券Aを10株購入し，収益を500円を得られることができていました．

ある1つの株券の銘柄について，$t$期目の株価を$S_t$とすると，$t$期の株価収益率$r$は，

r=\frac{S_{t+1}-S_t}{S_t}

によって計算することができます1．これは投資金額1単位に対する収益額を意味します．

このとき，上で定義した株価収益率によって，株券Aと株券Bの投資効率$r_A$と$r_B$を計算すると，

r_A=\frac{150-100}{100}=0.5=50\%

r_B=\frac{1050-1000}{1000}=0.05=5\%

となります．したがって，株券Aは，株券Bの10倍投資効率が高いことがわかります．

下の表は，三菱自動車とJT（日本たばこ産業）の株価を2020年8月3日から8月31日までを１日ごとに集計したものです．Yahoo Financeから得た株価データです．株価のとなりに日ごとの収益率も計算しています．右のグラフは株価データを基に作成した各社の株価の推移のグラフです．

各社の収益率の平均について，三菱自動車は，0.0109，JTは0.0009となります．この平均値を近い将来の期待できる収益率と考えると，9月は三菱自動車に投資する方が，JTに投資するよりも大きなリターンが期待できるといえます．

投資に伴うリスク（収益率の分散）

投資におけるリスクは，不確実性（収益率の分散）という意味です．つまり，損失の可能性と利益の可能性はどちらもリスクといいます．リスクが高いというのは，損失の可能性が高いということに加えて，利益の可能性も高いということを意味します．

三菱自動車とJTの日ごとの収益率をグラフにすると以下のようになります．三菱自動車は収益率の変動が大きく，大きく損をする可能性も高いが，大きく利益を得られる可能性も高いことがわかります．JTは三菱自動車よりも変動が小さいので，大きく損をすることも少ないが，大きく利益を得られる可能性も少ないということがみて理解できると思います．

三菱自動車は収益率の変動が大きい，JTは変動が小さい．これを測定するには収益率の分散（標準偏差）を調べます．これがリスクの指標となります．収益率の分散は，N個の収益率データ$X=(X_1,X_2,...,X_N)$に対して，平均を$E[X]$とすると，分散$V[X]$は，

V[X]=\frac{1}{N}\sum_{i=1}^N(X_i-E[X])^2

と定義されます1．

これを用いて，2社の収益率の分散を計算すると，上の表にも示した通り，三菱自動車は，0.0007，JTは0.0001となります．したがって，この数値を比較しても，三菱自動車はリスクが高く，JTはリスクが低いことがわかります．

投資の効率性（シャープ・レシオ）

株価収益率は，投資金額に対してどれくらい収益が得られたかがわかりました．しかし、各銘柄の株価収益率の比較では、投資家がとるリスクが考慮されていません．

「リスクに見合うリターンを得ているか」という投資効率はシャープ・レシオという指標を使って，数値化することができます．この数値が大きいほど、小さなリスクで大きな投資リターンを上げたことになります2．

例えば、株券A，Bともに，ある期間において，平均リターンが10%だったとしても，Aはリスクの大きい商品（標準偏差：5%），Bはリスクの小さい商品（標準偏差：8%）であれば、Aのほうが効率の良い投資結果といえます。

ある一定期間の株価収益率$E[X]$，無リスク資産の収益率$r$，標準偏差$\sigma=\sqrt{V[X]}$とすると，対象期間のシャープ・レシオは

 \frac{E[X]－r}{\sigma}

によって計算することができます．つまり，シャープ・レシオは，リスク（標準偏差）1単位当たりの超過リターン（リスクゼロでも得られるリターンを上回った超過収益）といえます．

無リスク資産の収益率は，リスクがゼロと見なされる資産の利子率です．3ヵ月国債の金利などが使われるのが一般的で，現在は0％として計算されることが多いようです．

各商品のシャープ・レシオは以下の通りです．株券Aの方がより大きい値となっているので，株券Bと比べ，株券Aはリスクに見合うリターンを得ているということがわかります．

  • Aのシャープ・レシオ$＝(10－0)÷5＝2$
  • Bのシャープ・レシオ$＝(10－0)÷8＝1.25$

三菱自動車とJTの例で，三菱自動車のシャープ・レシオは，0.40206となり，JTのシャープ・レシオは0.08732となります．この期間において，三菱自動車は，リスクを考慮しても，効率よく利益を出せているといえます．

日経225全銘柄の投資効率を分析

時系列データを収集する

まずは，以下のサイトを参考にして，日経225銘柄の証券コードのリストを作成します．

今回は以下のようにnikkei225.csvにまとめました．各銘柄の証券コードを縦に並べただけのcsvファイルです．

nikkei225.csv
1332
1333
1605
1721
．．．
9766
9983
9984

次に，データの取得には，Pythonのpandas_datareaderライブラリを使います．これを使うと，Yahoo Financeから，株価データを取得することができます．csvのファイルの読み書きは，PythonのPandasライブラリを使います．

以下のプログラムでは，nikkei225.csvでまとめた銘柄リストを基に，各銘柄の株価時系列データを取得します．株価データ取得後，data_StockPrice.csvという名前で株価の時系列データが保存されるようになっています．今回は，2020年8月1日から2020年10月31日の期間のみを対象としています．

※Pythonで取得したリクルートホールディングスの2020年10月30日の株価が397000となっていたので，おかしいと思い，Yahoo Financeのホームページを確認し，3970に変更しました（2020/12 現在）．

getStockPrice.py
import pandas as pd 
from pandas_datareader import data as wb

# 日経225全銘柄の証券コードを読み込み
df = pd.read_csv('nikkei225.csv', header=None)

# 証券コードリストを作成（証券コードの後ろに.Tを追加）
tickers = [str(name) + '.T' for name in list(df[0])]
sec_data = pd.DataFrame()

# 2020-8-1から2020-10-31までの時系列データをyahoo financeからダウンロード
for t in tickers:
   sec_data[t] = wb.DataReader(t, data_source='yahoo', start='2020-8-1', end='2020-10-31')['Adj Close']

# ダウンロードしたデータをcsvファイルに保存
sec_data.to_csv('data_StockPrice.csv')

収益率の期待値，分散，シャープ・レシオの計算をする

収益率の期待値，分散，シャープ・レシオの計算には，先ほどcsvファイルの読み書きにつかったPandasライブラリを使います．

以下のプログラムでは，各銘柄について，期待値$E$，分散$V$，シャープ・レシオを計算します．

analysis.py
import pandas as pd

# 全銘柄の株価データを読み込み
df = pd.read_csv('data_StockPrice.csv', index_col=0)

# 収益率を計算
df_returns = (df-df.shift(1))/df.shift(1)
# 標準偏差，　分散，シャープ・レシオを計算
df_std = pd.DataFrame(df_returns.var(), columns=['Variance'])
df_mean = pd.DataFrame(df_returns.mean(), columns=['Mean'])
df_sharpR = pd.DataFrame(df_returns.mean()/df_returns.std(), columns=['Sharpe Ratio'])

# 結果を結合
df_result = pd.concat([df_std, df_mean, df_sharpR], axis=1)

# 標準偏差と収益率のグラフを作成
df_result.plot.scatter(x='Variance', y='Mean')
# 結果を出力
df_result.to_csv('result.csv')

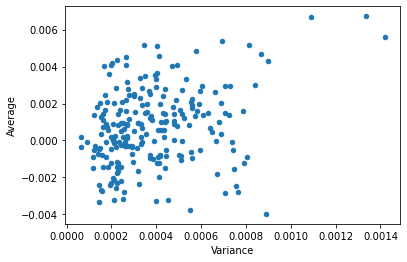
プログラムを実行し，計算した期待値，分散，シャープ・レシオの結果は以下のような形式で，result.csvに保存されます．また，期待値$E$と分散$V$の関係（平面座標の縦軸を期待値，横軸を分散）を図にしたものも出力されます．日経225全銘柄について，$E$と$V$の関係を示しているので，225個の点を表示しています．

result.csv
,Variance,Mean,Sharpe Ratio
1332.T,0.00024140689199941506,-0.0022015126549255965,-0.1416923338991954
1333.T,0.0004208576778149211,0.0010207643222448022,0.049757420171560714
1605.T,0.0003989382009706862,-0.0032687954488895186,-0.16365713051234088
1721.T,0.0001570271138713302,-0.0027079983857314694,-0.21610313980038348
...
9735.T,0.00015809883096170333,-0.0007889438846269872,-0.06274538448138048
9766.T,0.0003475459028979465,0.0035031691298778775,0.1879122179511506
9983.T,0.00016697549453860948,0.00401761594463755,0.3109152683157427
9984.T,0.0006676542525719263,-1.1105942231610932e-05,-0.0004298130528999511

以下の散布図が各銘柄の期待値$E$と分散$V$の関係を示したものです．

Figure 2020-12-01 195437.png

各銘柄の投資効率を考察

期待値と分散の関係図

以下の散布図は，Pythonから出力した「期待値$E$と分散$V$の関係を示す図」と同様なものです．さらに，点にラベル（企業名）を加えました．

この図はできるだけリスクを回避したいと思う（リスク回避的な）投資家の利用を想定しています．このリスク回避的な投資家は，「収益率が高く，リスク（分散）が低い銘柄」に投資しようと考え，青，赤，緑で囲まれた領域にある銘柄を選ぶと考えられます．

リスク回避的な投資家の中でも，ある程度リスクに寛容な投資家，リスクを最重視する投資家，ある程度のリスクを取り，リスクに対する収益率を重視する投資家に分けられ，投資家の好みによって，選ぶであろう銘柄が異なります．以下ではそれぞれが選ぶべき銘柄について考察します．

  • リスクに寛容で収益率を重視する投資家：
    リスク回避的な投資家の中でも，ある程度リスクに寛容な場合，赤で囲まれた領域にある銘柄を選ぶべきです．この領域にある銘柄は，日本製鋼所，DeNA，NTTドコモですが，リスクに対する収益率を考えたとき，「日本製鋼所」が選ばれます．まずNTTドコモは，投資対象からはずれます．それは日本製鋼所の方が収益率が高く，リスクも小さいためです．同様にして，日本製鋼所はDeNAと同じくらいの収益率であり，DeNAよりリスクが抑えられています．したがって，リスク回避的な投資家の中で，ある程度リスクに寛容な投資家は，日本製鋼所を選ぶべきだといえます．※NTTドコモは2020年12月25日に上場廃止

  • リスクを重視する投資家：
    リスク回避的な投資家の中でも，さらにリスクを最重視する投資家は，左にある緑に囲まれた領域にある銘柄を見るべきです．この投資家が最も選びそうな銘柄は，日本たばこ産業（JT）だと考えられます．次に，伊藤忠商事，日立造船もリスクが低いので，リスクを重視する投資家は，これらの銘柄を選ぶべきだといえます．

  • リスクに対する収益率を重視する投資家：
    リスク回避的な投資家の中でも，ある程度のリスクを取り，ある程度の収益率（リスクに見合うリターン）を重視する投資家は，青で囲まれた領域にある銘柄を選びます．例えば，ファーストリテイリング，デンソー，東海カーボンなどはリスクに対する収益率が高いことがみてわかると思います．

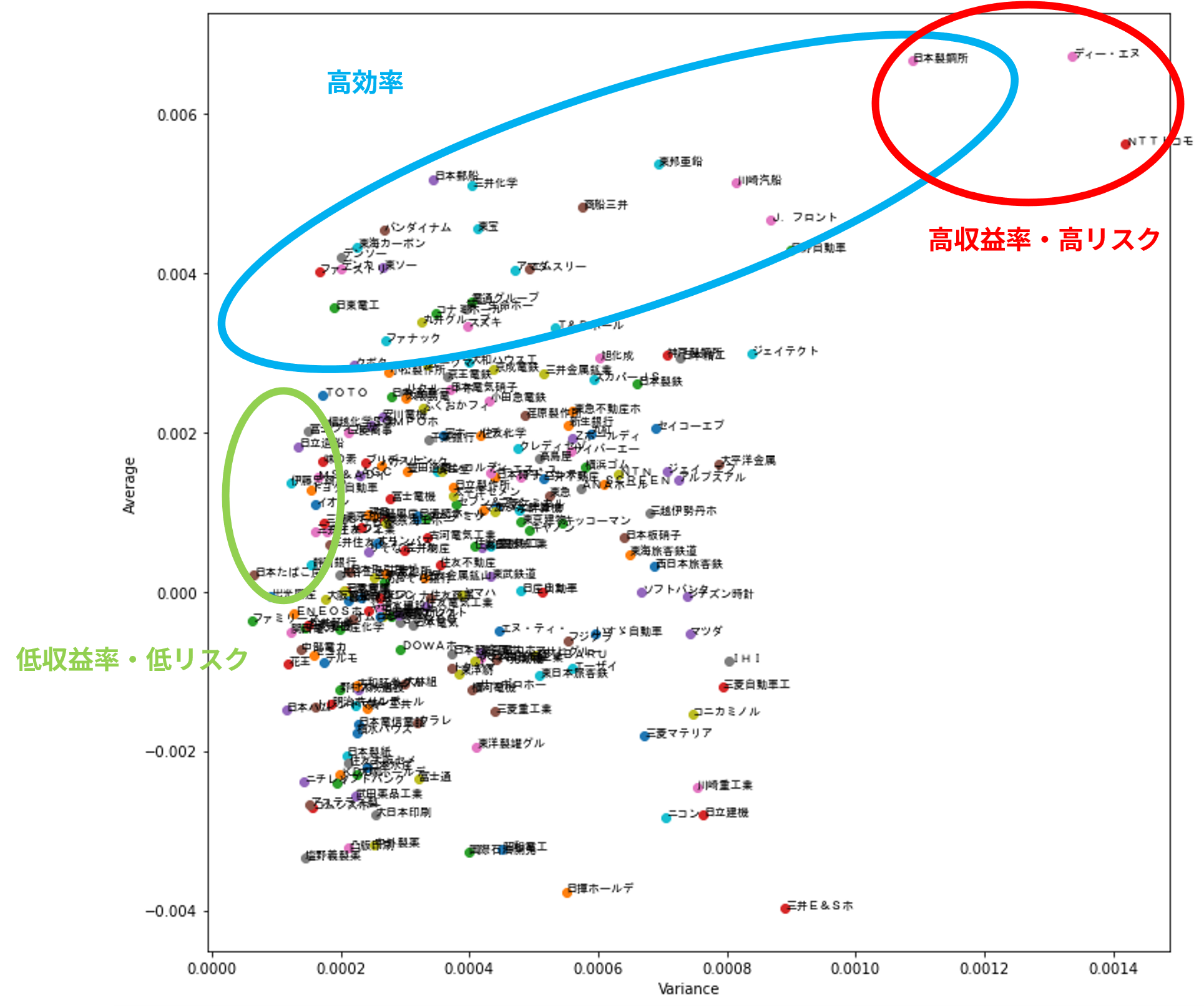
図2.png
※点がたくさんあるところは見にくくなっていますが，ご了承ください．また，見にくさを軽減するため，会社名をはじめの6文字で表現しています．

シャープ・レシオ

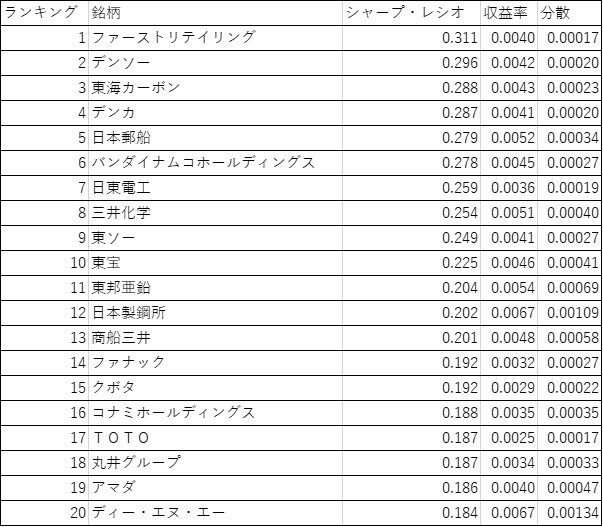
シャープ・レシオはリスクに対する収益率でした．以下はシャープ・レシオの高い銘柄を上から順に20銘柄分並べています．

やはり，ファーストリテイリング，デンソー，東海カーボンはリスクに対する収益率が高いことがわかります．日本製鋼所も12位と上位の方にいるので，収益率に対しリスクをとる価値がある銘柄だといえます．

期待値と分散の散布図の考察のところでも触れましたが，リスクに対する収益率を重視する投資家には以下の銘柄を選ぶということがシャープ・レシオの数値からもわかります．

図2.png

まとめ

株式投資における投資によるリターン（株価収益率），投資に伴うリスク（収益率の分散），リスクに対するリターン（シャープ・レシオ）の計算方法について紹介し，2020年8月1日から2020年10月31日の期間における日経225全銘柄を対象にPythonプログラムを用いて，この3つの指標について計算しました．

リスク回避的な投資家の中でも，ある程度リスクに寛容な投資家，リスクを最重視する投資家，ある程度のリスクを取り，リスクに対する収益率を重視する投資家に分類し，それぞれが選ぶべき銘柄について以下のように考察しました．

  • リスクに寛容で収益率を重視する投資家：日本製鋼所
  • リスクを重視する投資家：日本たばこ産業
  • リスクに対する収益率を重視する投資家：ファーストリテイリング，デンソー，東海カーボン

この結果は，時系列データの期間の取り方などによっても大きく変わります．また以上の3つの指標は，数理ファイナンスにおける基礎中の基礎にすぎません．したがって，投資で成功していくには，いろいろな期間で検証したり，3つの指標以外の指標も参考にすることが重要だというのは言うまでもないと思います．

本記事で載せたPythonプログラムは，特別なプログラミング技術は一切必要なく，プログラミング経験がすこしでもあれば，本記事の結果の再現がすぐに可能だと思います．

本記事で何か新しい知見が得られたり，株価を分析するための役に立てれば幸いです．

次回は以下の内容について，記事を書いていくので，興味ある方は見ていただけると嬉しく思います．

今後の予定
・「1000円以下のボラティリティが高い銘柄について調査」
・「2銘柄への分散投資について調査」

  1. 数理ファイナンス (放送大学教材 7051) 津野義道 著 ↩ ↩2

  2. 初めてでもわかりやすい用語集 ＳＭＢＣ日興証券 ↩

27
22
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
27
22

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?