はじめに
一般的に株価と金は逆相関すると言われています．
株価が大きく下落しても，保有資産が大きく減少しないよう，リスクヘッジとして，金に投資することがあります．
過去の記事で，効率的な投資を考えるには，収益率，リスク（収益率の分散）を考えることが重要だと紹介しました．
今回は株と金への分散投資によりリスクを軽減することを考えます．
S&P500と金への投資を想定して，どんな比率で投資すれば，リスクを最小限にできるかを様々な期間でPythonで計算してみました．
＜過去記事＞
・日経225全銘柄の投資効率を検証
・日経平均株価の30%は5銘柄で決まることを投資先選びに生かせるか？
分析結果と考察
まずはじめに分析結果から紹介します．
分析方法やPythonプログラムなど興味がある方は以下に載せてあるので，ご覧ください．
2019年12月1日から2020年11月30日までの期間で1日ごとにS&P500とSPDRゴールド･シェアというETFの時系列データを取得しました．
※ S&P500の時系列データは，本来であれば，どこかのETFのデータを採用するべきですが，今回は簡単のためS&P500の指数をそのまま利用しました．
取得したデータから，日々の収益率(%)を計算し，その日々の収益率から期待値（平均値）や分散（リスク）を計算しました（今回の記事では収益率を年率換算していません．1日で得られる収益率ままで分析しています．）．
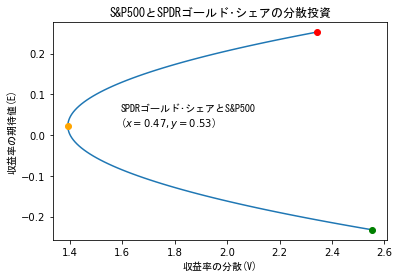
その結果を基にして，SPDRゴールド･シェアに$x$の比率，S&P500に$y$の比率で投資することを考えると，以下のグラフ（放物線）が得られます．ここで，$x$と$y$は$x+y=1$を満たすように選ぶとします．
図の下にグラフから読み取れることをまとめましたが，
S&P500に単独投資した場合は赤点で示されているような収益率の期待値と分散の関係になります（リスクが大きい分リターンも大きい）．金の場合は，緑点で示した関係になります．また$x=0.8$と$y=0.2$の比率で各銘柄に投資すると，単独投資では実現しなかった，リスクを最小にする資産構成が得られます（オレンジ点）．
リスクはできるだけ小さい方が良いが，ある程度リスクを許容可能でより高収益率を期待したい場合は，オレンジ点と赤点の間の放物線を参考に$x$と$y$の比率を決めることになります．
記事の一番下に別の期間で検証したものを載せておいたので，そちらもご覧ください（コロナ前の1年間の結果や最近の数か月の結果も計算してみました）．
【パラメータ】
検証期間：1年間（2019年12月1日から2020年11月30日まで）
投資銘柄：S&P500，SPDRゴールド・シェア
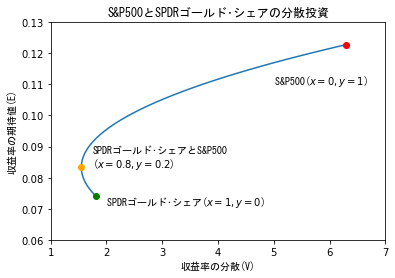
＜要点＞
- 緑点（$x=1$，$y=0$）はSPDRゴールド･シェアにすべての資金を投資したときの投資効率を示す．
- 同様に，赤点（$x=0$，$y=1$）はS&P500にすべての資金を投資したときの投資効率を示す．
- 適切な資産構成（ポートフォリオ）にするとリスク（収益率の分散）を最小化して，収益率の期待値を上昇させることが可能である（オレンジ点）．
- その構成は，SPDRゴールド･シェア$x=0.8$，S&P500$y=0.2$の比率である．このとき，ポートフォリオの収益率の期待値は，0.083，分散は1.550である．
- したがって，リスクを最小化したい投資家には上記の資産構成で投資する戦略を提案することができる．
資産構成（ポートフォリオ）の期待収益率とリスク
ここでは，2銘柄へ分散投資したときの期待収益率とリスクの計算方法について紹介します．
まず，投資家が保有している金融商品の組み合わせをポートフォリオといいます．
※ 数学の詳細な解説は数理ファイナンス (放送大学教材 7051)で記述されています．以下では詳しい説明は省略し要点のみを紹介していきます．
ポートフォリオの期待収益率
2つの証券A，Bへの分散投資を考えます．
2銘柄への分散投資は，以下の設定で行うと仮定します．
- A証券には$x$の比率だけ，B証券には$y$の比率だけ投資を行う（$x+y=1$）
- 時期$t$における証券Aの収益率を$r_t$，証券Bの収益率を$s_t$とする
時期$t$における，このポートフォリオの収益率は，$P(x,y)=x r_t+y s_t$となります．
したがって，ポートフォリオの収益率$P(x,y)$の平均値は，
E(x,y)=x \bar{r} + y\bar{s}
と計算できます．$\bar{r}$は証券Aの収益率の平均値，$\bar{s}$は証券Bの収益率の平均値を意味しています．
ポートフォリオのリスク
時期$t$におけるポートフォリオの収益率$P(x,y)$の分散値（ポートフォリオのリスク）を$V(x,y)$とします．
分散$V(x,y)$の定義は各期のデータと平均値との差の2乗を平均したものです．したがって，その定義に従い，$V(x,y)$を計算すると，
V(x,y)=x^2V(A,A)+2xyV(A,B)+y^2V(B,B)
となります．$V(A,A)$は証券Aの収益率の分散値，$V(B,B)$は証券Bの収益率の分散値，$V(A,B)$は証券AとBの収益率の共分散です．この共分散$V(A,B)$は，証券A，Bの組み合わせによって負の値をとることがあるので，分散が小さくなります．
分析プログラム（Python）
時系列データを収集する
以下のプログラムを実行すると，SPDRゴールド･シェアとS&P500の1年分のデータが得られます．
データはcsvファイル（data_StockPrice.csv）に保存されます．
データの取得には，Pythonのpandas_datareaderライブラリを使います．以下のプログラムではYahoo! Financeから，株価データを取得しています．
import pandas as pd
from pandas_datareader import data as wb
# SPDRゴールド･シェアとS&P500の名前リスト
tickers = ['1326.T' ,'^GSPC']
sec_data = pd.DataFrame()
# 2019-12-1から2020-11-30までの時系列データ（終値）をYahoo! Financeからダウンロード
for t in tickers:
sec_data[t] = wb.DataReader(t, data_source='yahoo', start='2019-12-1', end='2020-11-30')['Adj Close']
# ダウンロードしたデータをcsvファイルに保存
sec_data.to_csv('data_StockPrice.csv')
ポートフォリオの収益率の期待値と分散を計算する
期待値と分散の計算はPandasの機能を使い計算していく．図の作成はmatplotlibを使用する．
以下を実行すると，はじめ紹介したような図が作成される．
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 全銘柄の株価データを読み込み
df = pd.read_csv('data_StockPrice.csv', index_col=0)
# 収益率の計算
df_returns = (df-df.shift(1))/df.shift(1)*100
# 収益率の分散，平均，共分散
ave = df_returns.mean()
var = df_returns.var()
print('Average:'); print(ave)
print('Variance:'); print(var)
print('Covariance:\n', df_returns.cov().loc['1326.T','^GSPC'])
# データを生成
E = [x*ave['1326.T']+(1-x)*ave['^GSPC'] for x in np.linspace(0, 1, 100)]
V = [x**2*var['1326.T']+2*x*(1-x)*df_returns.cov().loc['1326.T','^GSPC']+(1-x)**2*var['^GSPC'] for x in np.linspace(0, 1, 100)]
# 放物線描画
plt.plot(V,E)
# 点追加
plt.plot([V[V.index(min(V))]], [E[V.index(min(V))]], 'o', c='orange')
plt.plot([V[0]], [E[0]], 'o', c='r')
plt.plot([V[-1]], [E[-1]], 'o', c='g')
# タイトル設定
plt.title('S&P500とSPDRゴールド･シェアの分散投資', fontname="MS Gothic")
# 軸ラベル設定
plt.ylabel('収益率の期待値(E)', fontname="MS Gothic")
plt.xlabel('収益率の分散(V)', fontname="MS Gothic")
# テキスト追加
plt.text(V[V.index(min(V))]+0.2, E[V.index(min(V))],'SPDRゴールド･シェアとS&P500\n($x={}, y={}$)'.format(V.index(min(V))/100, round(1-V.index(min(V))/100,3)), fontname="MS Gothic")
※ Spyderでプログラムを実行すると，そのまま図が表示されるが，他の実行環境ではプログラムに少し記述を追加が必要とする場合がある．
追加検証
記事の一番最初に紹介したものと同じものです．比較のため載せてあります．
- 緑点（$x=1$，$y=0$）はSPDRゴールド･シェアにすべての資金を投資したときの投資効率を示す．
- 赤点（$x=0$，$y=1$）はS&P500にすべての資金を投資したときの投資効率を示す．
- オレンジ点は最小リスクでポートフォリオを組む時の投資効率を示す．
【パラメータ】
検証期間：1年間（2019年12月1日から2020年11月30日まで）
投資銘柄：S&P500，SPDRゴールド・シェア
コロナウイルス感染拡大前の1年間
【パラメータ】
検証期間：1年間（2019年1月1日から2019年12月31日まで）
投資銘柄：S&P500，SPDRゴールド・シェア
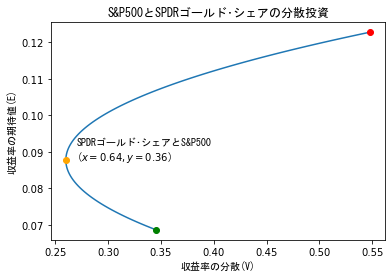
- はじめに紹介したもの（コロナウイルス感染拡大を含む1年間）と比べて，収益率の期待値の範囲はほぼ同じですが，分散が桁違いに違うということがわかりますね．．．
- また，このとき，リスクを最小化するには上のものと比較して，S&P500により大きな比率で投資したほうがよいこともわかります．．
【パラメータ】
検証期間：3年間（2017年12月1日から2020年11月30日まで）
投資銘柄：S&P500，SPDRゴールド・シェア
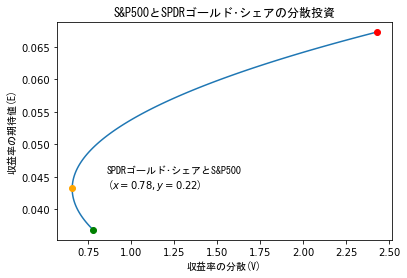
- 3年間で考えたときも，リスクを最小化するには，1年間（2019年12月1日から2020年11月30日まで）と同じような資産構成にするべきだということがわかります．
- また，1年間のものと比べて分散や収益率が小さくなっていると思います．コロナの影響でしょうか．
【パラメータ】
検証期間：8か月（2020年4月1日から2020年11月30日まで）
投資銘柄：S&P500，SPDRゴールド・シェア
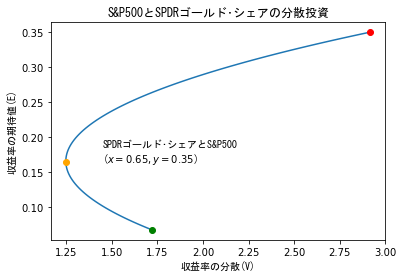
【パラメータ】
検証期間：4か月（2020年8月1日から2020年11月30日まで）
投資銘柄：S&P500，SPDRゴールド・シェア
＜次回以降の予定＞
・グロース株のPSRを調査
・コロナ前後でのグロース株のPSRの変化，バリュー株のPERの変化を調査