More than 3 years have passed since last update.

【5年分データ分析】MACDの買いサインから上がる確率を検証しました

Last updated at 2021-01-30Posted at 2021-01-30

＜あらすじ＞
単純移動平均の遅延を改善したMACDがどれだけ有用なのか？
TOPIX500銘柄を対象に5年分のデータを使って検証しました。

＜結論＞
・単純移動平均を使ったゴールデンクロスよりも数％ではあるが、数日後に上昇する確率が高い
・MACDの信頼度はゴールデンクロスの位置が影響する

#きっかけ
【5年分データ分析】ゴールデンクロスの数日後に株価は上がっているのかでゴールデンクロスの検証を行いました。

結果は、条件に関わらず数日後上昇しいる確率は約50％であり、
ゴールデンクロス単体だけで買いタイミングを判断してはいけないという結論に至りました。
※ 詳細は記事をご覧ください。

そのような結果となった理由として
ゴールデンクロスに単純移動平均を使用していることが考えられます。
単純移動平均は一定期間の株価の平均値を線で結んだもののため、移動平均線の動きは株価の動きよりも遅延します。

これにより買いタイミングを判断するには遅すぎるのです。

そこで、今回は**株価の変化に敏感な「MACD」**について検証したいと思います。

#MACD（マックディー）
簡単にMACDについて説明します。
移動平均を応用したテクニカルの手法の一つで、2つの移動平均線を使用して買い/売りタイミングを判断します。
1つ目の移動平均線：価格の変化に敏感なMACDライン

$$ MACD = 短期EMA - 長期EMA $$

2つ目の移動平均線：変化に緩やかに反応するシグナルライン

$$ シグナル = MACDの単純移動平均 $$

$EMA$とは指数平滑移動平均と呼ばれるもので、単純移動平均に比べて振幅が小さく、反応が早い特徴があります。
詳しくはこちら（MACD、EMA）などで解説されています。

【MACDの買いサイン】
① ゴールデンクロス：MACDがシグナルを下から上に突き抜けた時
② ゼロクロス：MACDが0を突き抜けた時（マイナス⇒プラス）

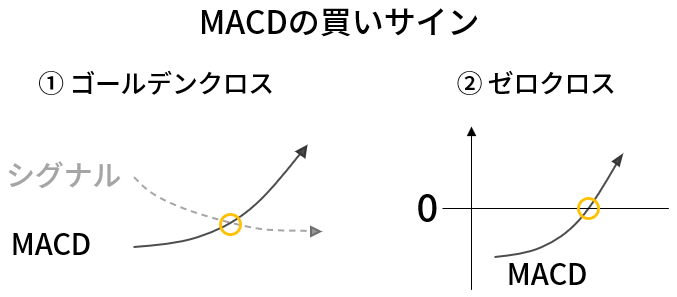
この2パターンがMACDの買いサインです。

TOPIX500銘柄の過去5年分のデータを使って
この2種類の買いサインの数日後に、株価が上がっているのかを検証します。

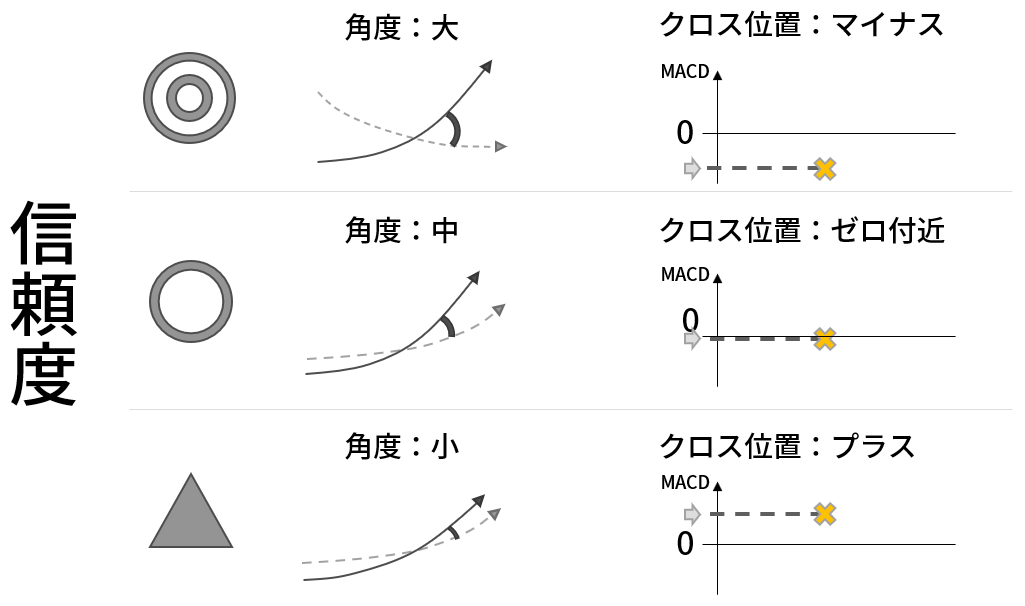
信頼度

MACDの買いサインには信頼度があると言われています。
直観的にも交差の角度が大きいほど上昇が見込めると考えられます。
また、MACDの値が低いときにゴールデンクロスが現れたときほど信頼度が高いです。
これは「MACDがマイナス＝長期的に株価が下落 ⇒ ゴールデンクロス＝トレンドが転換」となるためです。

▼MACDの信頼度（ゴールデンクロス）

ゼロクロスの場合は単純にMACDの傾きが信頼度となります。

これらの信頼度がどれだけ信頼できるのかも検証したいと思います。

#検証方法
大まかな流れはTOPIX500銘柄を対象に5年分のデータからMACDの買いサインを見つけ、その数日後に株価が上がっているのかを調査します。また、交差時の角度や位置から信頼度別に分類して評価します。

一旦、検証パラメータを羅列しますが、後ほど例を使って説明します。

【検証期間】
2015年1月1日～2020年1月20日の約5年間

【対象銘柄】
TOPIX500銘柄

【移動平均の期間】

短期EMA：6日，長期EMA：13日，シグナル：4日
短期EMA：6日，長期EMA：19日，シグナル：9日
短期EMA：8日，長期EMA：17日，シグナル：9日
短期EMA：9日，長期EMA：26日，シグナル：9日
短期EMA：12日，長期EMA：26日，シグナル：9日（最も使われる）
短期EMA：19日，長期EMA：39日，シグナル：9日
※「MACD 期間」で検索して出てきたものを採用

【株価の上昇を確認する日】

1日後
3日後
5日後
10日後

【条件】
＜ゴールデンクロス＞

なし
角度：30度以上
角度：45度以上
角度：60度以上
位置：MACDが株価の0.5%以下
位置：MACDが株価の1%以下
＜ゼロクロス＞
なし
角度：80度以上

例

下図のようにゴールデンクロス/ゼロクロスの数日後に株価が上昇しているかを確認します。
▼検証方法の概要（ゴールデンクロス）

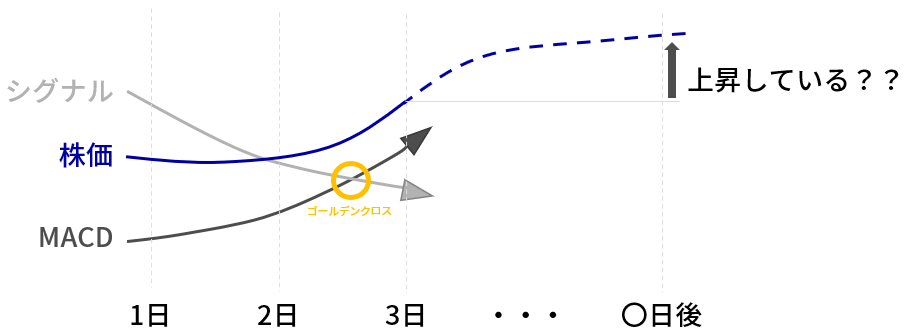
▼検証方法の概要（ゼロクロス）

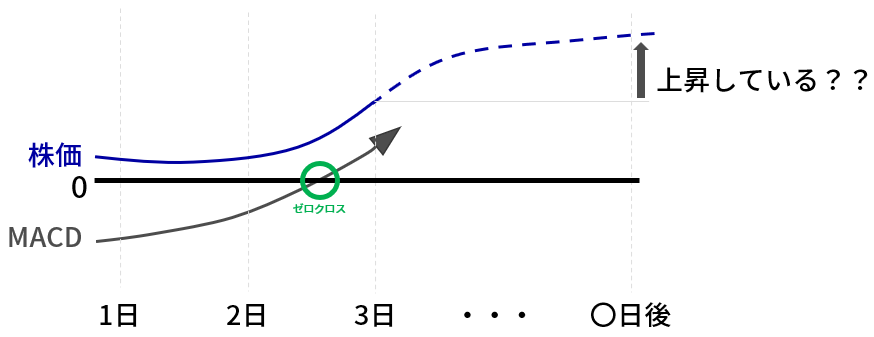
次に、信頼度の判断方法です。
信頼度がどれだけ信頼できるのかを検証するために、ゴールデンクロスに条件を加えます。
条件の判断基準となる角度は下図の方法で求めます。
▼信頼度の判断方法（角度）

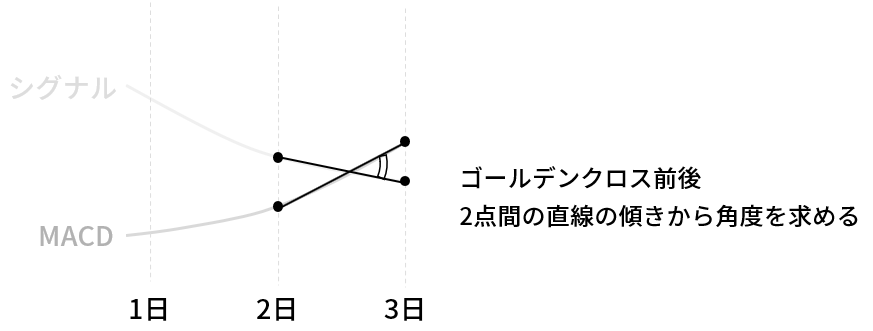
ゼロクロスの場合はシグナルではなく、ゼロのラインとの角度を求めます。

MACDのゴールデンクロスの位置については下図のように割合で考えます。
MACDは株価を使った移動平均のため、株価の大きさによって振幅が異なるからです。
▼信頼度の判断方法（位置）

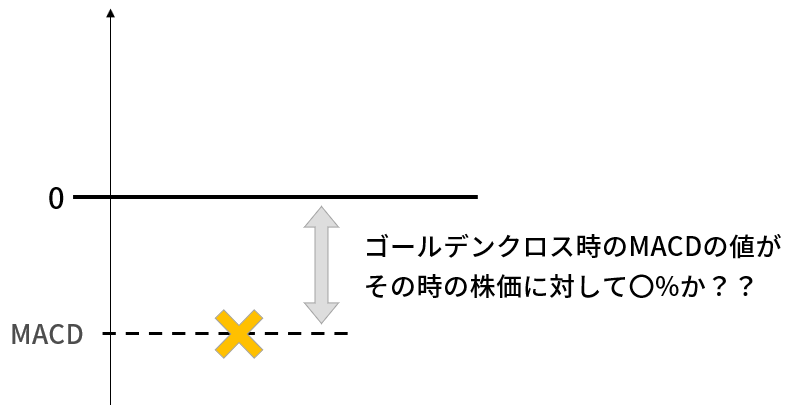
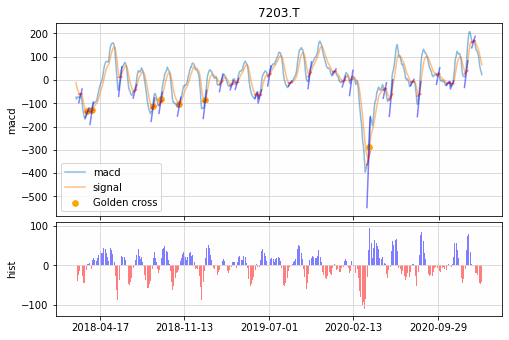
例としてトヨタ自動車の場合を記載します。
見やすさのために、2018年1月～2021年1月の約3年分のデータを使いました。
黄色の丸がゴールデンクロスのタイミングを示します。
ゴールデンクロス：MACDがシグナルを下から上に突き抜ける現象
⇒ 青線が黄線を下から上に突破
▼短期EMA：12日，長期EMA：26日，シグナル：9日の場合

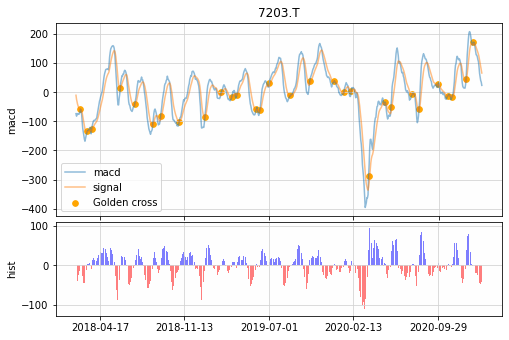
「hist」はMACDとシグナルの差を算出したものです。
クロスのタイミングと2つのラインの幅が視覚的にわかります。

次は信頼度を検証するために条件をつけてゴールデンクロスを取捨選択します。
下図は角度：45度以上のゴールデンクロスのみにしたものです。
▼角度の条件からゴールデンクロスを選択（角度：45度以上の場合）

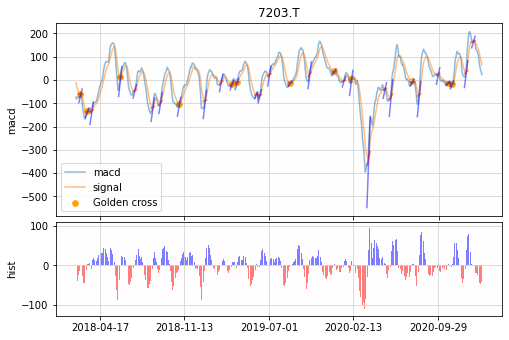
下図は位置：MACDが株価の1%以下のゴールデンクロスのみにしたものです。
MACDの値が低いものだけ選択します。
▼交差の位置からゴールデンクロスを選択（位置：MACDが株価の1%以下の場合）

最後に選択されたタイミングから〇日後上昇しているか確認します。

以上の方法でTOPIX500銘柄を対象に5年分のデータを検証しました。
※検証のPythonプログラムは記事の最後に記載

#検証結果
ここでは結果の一部を記載します。
その他の結果は記事の最後にまとめて記載します。
使用するデータは前述の通りTOPIX500銘柄の5年間です。

【移動平均の期間】

短期EMA：8日，長期EMA：17日，シグナル：9日（最も結果が良い）
短期EMA：12日，長期EMA：26日，シグナル：9日（最もよく使われる）

【株価の上昇を確認する日】

1日後
3日後
5日後
10日後

【条件】
＜ゴールデンクロス＞

なし
角度：45度以上
位置：MACDが株価の1%以下
＜ゼロクロス＞
なし
角度：80度以上

早速ですが結果を表にまとめました。
【結果】
＜ゴールデンクロス＞
▼短期EMA：8日，長期EMA：17日，シグナル：9日の結果

▼短期EMA：12日，長期EMA：26日，シグナル：9日の結果

＜ゼロクロス＞
▼短期EMA：8日，長期EMA：17日，シグナル：9日の結果

▼短期EMA：12日，長期EMA：26日，シグナル：9日の結果

まずゴールデンクロスとゼロクロスを比較すると
ゴールデンクロスは49.1％～55.5％と条件によっては上昇が確認できます。
ゼロクロスは47.8％～51.2％と条件がある/なしに関わらず約50%です。
特に短期EMA：8日，長期EMA：17日，シグナル：9日のゴールデンクロスでは
条件**「位置：MACDが株価の1％以下」のとき5日後に55.5％上昇する**という結果が得られました。
これらの結果は単純移動平均を使用したゴールデンクロスよりも、数％ではありますが上昇する確率が高いです。

移動平均の設定期間によっても結果は異なり
最も使われる短期EMA：12日，長期EMA：26日，シグナル：9日よりも、短期EMA：8日，長期EMA：17日，シグナル：9日の方が上昇率は少し高めです。

また、MACDの信頼度は角度の情報より、ゴールデンクロスの位置が重要であることが分かります。
MACDの値が低いときにゴールデンクロスが現れたときほど信頼度が高いことがデータから読み取れます。

上昇する確率を数％でも上げられるなら
「MACDのゴールデンクロスは買いサインとして有用である」と言えるでしょう。

#まとめ
前回の検証から単純移動平均線を使ったゴールデンクロスは、買いタイミングを判断するには遅すぎると考えました。
そこで、今回は株価の変化に敏感な「MACD」についてTOPIX500銘柄の5年分のデータで検証しました。
結果は数%ではありますが、単純移動平均線よりMACDを使ったゴールデンクロスの方が上昇する確率が高いという結果が得られました。また、MACDの信頼度はゴールデンクロスの位置が重要であることも分かりました。
投資において未来に上昇する確率が数％でも上がるというのは、買いサインとして有用であると考えられます。
（私の予想ではもう少し高い確率が得られるのではないかと思っていたため少し残念です...）

MACDには過熱感がわからないという特徴があります。
過熱感とは「買われすぎ」や「売られすぎ」といった相場の勢いのことです。
MACDは2つの移動平均線の差であり上限/下限がないため、その過熱感が読み取れないのです。
過熱感を表す指標を組み合わせることで、MACDの精度を高められるかもしれません。

#次は
過熱感を表す指標には「RSI」「ストキャスティクス」「移動平均線乖離率」などが有名です。
それぞれの指標について個別に検証するか、MACDと組み合わせて精度が上がるのか検証してみたいと思います。

#結果の一覧
検証条件と結果の一覧
【検証期間】
2015年1月1日～2020年1月20日の約5年間

【対象銘柄】
TOPIX500銘柄

【移動平均の期間】

短期EMA：6日，長期EMA：13日，シグナル：4日
短期EMA：6日，長期EMA：19日，シグナル：9日
短期EMA：8日，長期EMA：17日，シグナル：9日
短期EMA：9日，長期EMA：26日，シグナル：9日
短期EMA：12日，長期EMA：26日，シグナル：9日（最も使われる）
短期EMA：19日，長期EMA：39日，シグナル：9日

【株価の上昇を確認する日】

1日後
3日後
5日後
10日後

【条件】
＜ゴールデンクロス＞

なし
角度：30度以上
角度：45度以上
角度：60度以上
位置：MACDが株価の0.5%以下
位置：MACDが株価の1%以下
＜ゼロクロス＞
なし
角度：80度以上

▼ゴールデンクロスの条件1~4

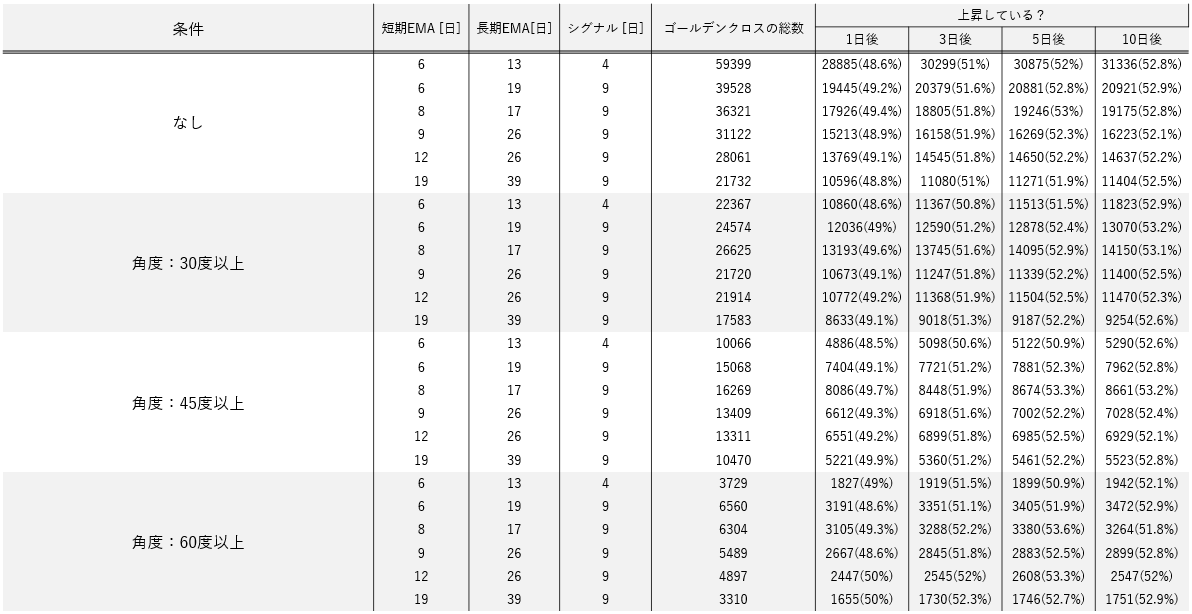
▼ゴールデンクロスの条件5,6

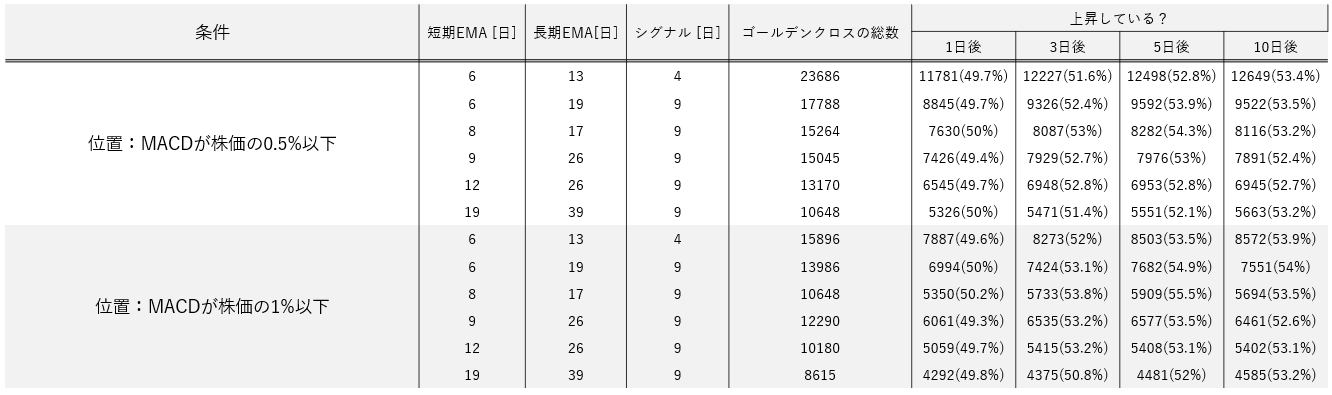
▼ゼロクロス

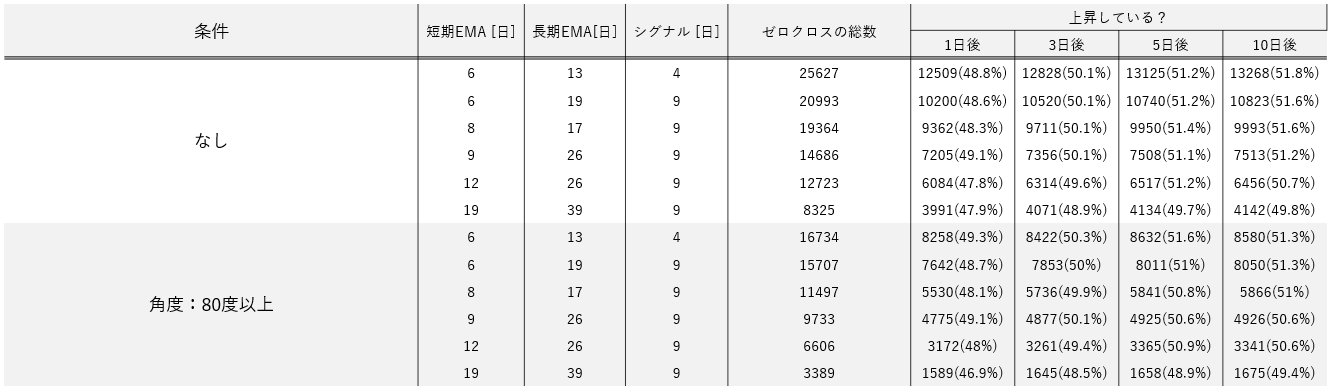
#検証プログラム
ゴールデンクロス検証のプログラムを記載します。
ゼロクロスの場合も基本的な流れは同様のため省略します。

import trade_package as tp # 株価分析用に自作した関数をまとめたもの
import pandas as pd
import numpy as np

# 銘柄コードの読み込み
stock = tp.get.topix500()

## resultデータフレーム
day = [1,3,5,10]    # 〇日後に上昇しているかの〇を設定
col=["g_p_count"]   # ゴールデンクロスの総数
period = [[6,13,4],[6,19,9],[8,17,9],[9,26,9],[12,26,9],[19,39,9]] # 移動平均の期間
for d in day:
    col.append("roc_d"+str(d)+"_plus")
result = pd.DataFrame(data=0,index=range(len(period)),columns=col)


for code in stock.code:
    print(code)
    # 用意した株価データの読み込み
    read_data = tp.get.price(code)
    
    for p in range(len(period)): 
        data = read_data.copy()
        # MACDを計算
        tp.tech.macd(data, fastperiod=period[p][0], slowperiod=period[p][1], signalperiod=period[p][2])
        data["g_point"] = False
        
        # ゴールデンクロスのタイミングを取得
        for i in range(len(data.index)-1):
            if(data.macd[i]<data.signal[i] and data.macd[i+1]>data.signal[i+1]):
                data["g_point"].iat[i+1] = True
               
        # ゴールデンクロス時の傾き/角度を算出
        data["macd_line"] = np.nan
        data["signal_line"] = np.nan
        data["macd_slop"] = np.nan
        data["signal_slop"] = np.nan
        data["line_deg"] = np.nan
        for g in data.index[data.g_point]:
             # 2点間の直線を算出
             a1 = data.macd[g] - data.macd[len(data.Close[:g])-1-1]
             b1 = data.macd[g] - a1*len(data.Close[:g])
             data["macd_slop"].at[g]=a1 
             a2 = data.signal[g] - data.signal[len(data.Close[:g])-1-1]
             b2 = data.signal[g] - a2*len(data.Close[:g])
             data["signal_slop"].at[g]=a2
             data["line_deg"].at[g] = np.rad2deg(np.arctan(abs((a1-a2)/(1+a1*a2))))
             # plot用に直線データ追加
             for i in range(7):
                 x = len(data.Close[:g])-1+i-3
                 data["macd_line"].iat[x]= a1*x+b1
                 data["signal_line"].iat[x]= a2*x+b2
                
        # 除くゴールデンクロスを選択        
        for g in data.index[data.g_point]:
            # 角度の条件設定
            if(data["line_deg"].at[g] < 30):
                data["g_point"].at[g] = False
            
            # 位置
            # if(data["macd"].at[g] > -data["Close"].at[g]*0.01):
            #     data["g_point"].at[g] = False
        
        # 〇日後に上昇しているか確認
        for g in data.index[data.g_point]:
            for d in day:
                if(len(data.Close[:g])+d<=len(data.Close)):
                    data.at[g,"roc_d"+str(d)] = (data.Close[len(data.Close[:g])+d-1]-data.Close[g])/data.Close[g]*100
                else:
                    data.at[g,"roc_d"+str(d)] = (data.Close[-1]-data.Close[g])/data.Close[g]*100

                if(data.at[g,"roc_d"+str(d)]>0):
                    data.at[g,"roc_d"+str(d)+"_point"] = 1
                else:
                    data.at[g,"roc_d"+str(d)+"_point"] = 0
        
        # 上昇していたらカウンタを加算
        data.dropna(inplace=True)
        if(len(data.index[data.g_point])>0):
            result["g_p_count"].iat[p] += len(data.index)
            for d in day:
                result["roc_d"+str(d)+"_plus"].iat[p]+=sum(data["roc_d"+str(d)+"_point"])

print(result)

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up