<あらすじ>
テクニカル分析の初歩「ゴールデンクロス」が実際にはどれだけ役に立つのか?
TOPIX500銘柄を対象に5年分のデータを使って検証しました。
<結論>
・様々な条件での実験で上昇している確率は約50%
・ゴールデンクロス単体だけで買いタイミングを判断してはいけない
ゴールデンクロス
ゴールデンクロス:短期の移動平均が長期の移動平均を下から上に突き抜ける現象
⇒ 上昇期入りのシグナル/買いシグナル/買いサイン
テクニカル分析に興味を持った人は必ず聞いたことがあるのではないでしょうか。
一番最初に学ぶテクニカル分析と言っても過言ではないと思います。
そんなゴールデンクロスですが、大きな欠点があります。
「だましには要注意」「確実に上昇するとは言い切れない」「あくまで傾向であり必ずとは限りません」
ゴールデンクロスを紹介している記事の多くが保険を掛けています。
そんなこと言っていたら結局ゴールデンクロスを参考にしていいのかわからないと思うわけです。
※ だまし:誤ったサイン
そこで過去のデータを使ってゴールデンクロスの数日後に株価は上がっているのか検証したいと思います。
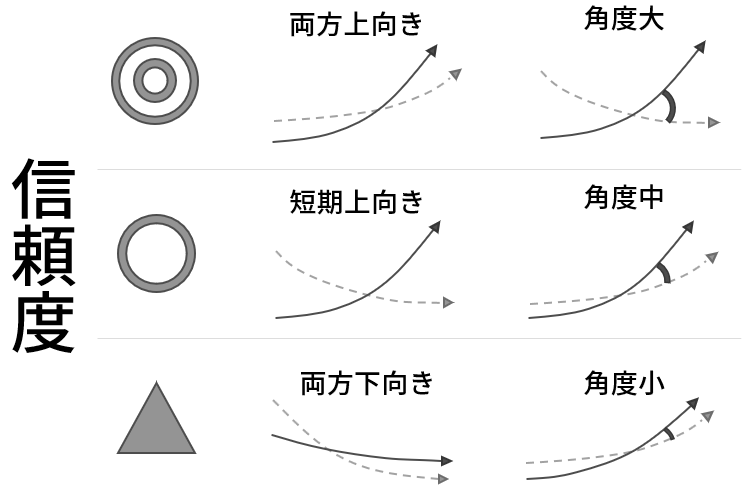
信頼度
ゴールデンクロスには信頼度があると言われています。
直観的にも交差の角度が大きいほど上昇が見込めると考えられます。
この信頼度がどれだけ信頼できるのかも検証したいと思います。
検証方法
大まかな流れはTOPIX500銘柄を対象に5年分のデータからゴールデンクロスしたタイミングを見つけ、その数日後に株価が上がっているのかを調査します。また、交差時の方向や角度から信頼度別にゴールデンクロスを分類して評価します。
一旦、検証パラメータを羅列しますが、後ほど例を使って説明します。
【検証期間】
2015年1月1日~2020年1月8日の約5年間
【対象銘柄】
TOPIX500銘柄
【移動平均の期間】
- 短期:5日,長期:25日
- 短期:5日,長期:50日
- 短期:5日,長期:75日
- 短期:25日,長期:50日
- 短期:25日,長期:75日
【株価の上昇を確認する日】
- 1日後
- 3日後
- 5日後
- 10日後
【条件】
- なし
- 方向:短期線が上向き,長期線が下向き
- 方向:短期線が上向き,長期線も上向き
- 角度:30度以上
- 角度:45度以上
- 角度:60度以上
- 方向:短期線が上向き,長期線も上向き かつ 角度:60度以上
例
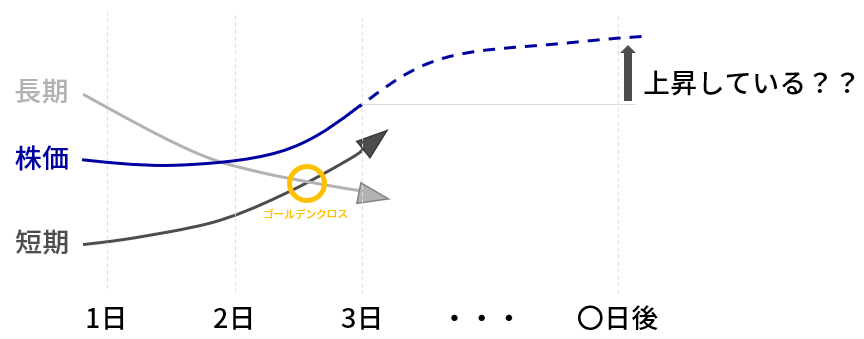
下図のようにゴールデンクロスの数日後に株価が上昇しているかを確認します。
図は交差を確認するために大袈裟に描いてありますが、実際には交差の点と日付の間隔はもっと狭いです。
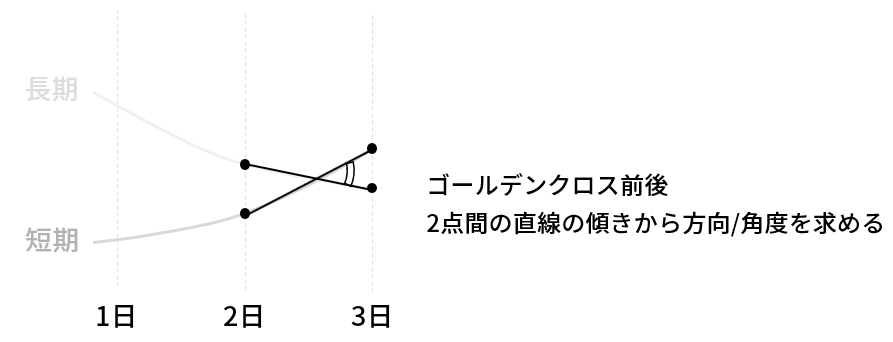
▼検証方法の概要
次に、信頼度の判断方法です。
信頼度がどれだけ信頼できるのかを検証するために、ゴールデンクロスに条件を加えます。
条件の判断基準となる方向/角度は下図の方法で求めます。
▼信頼度の判断方法
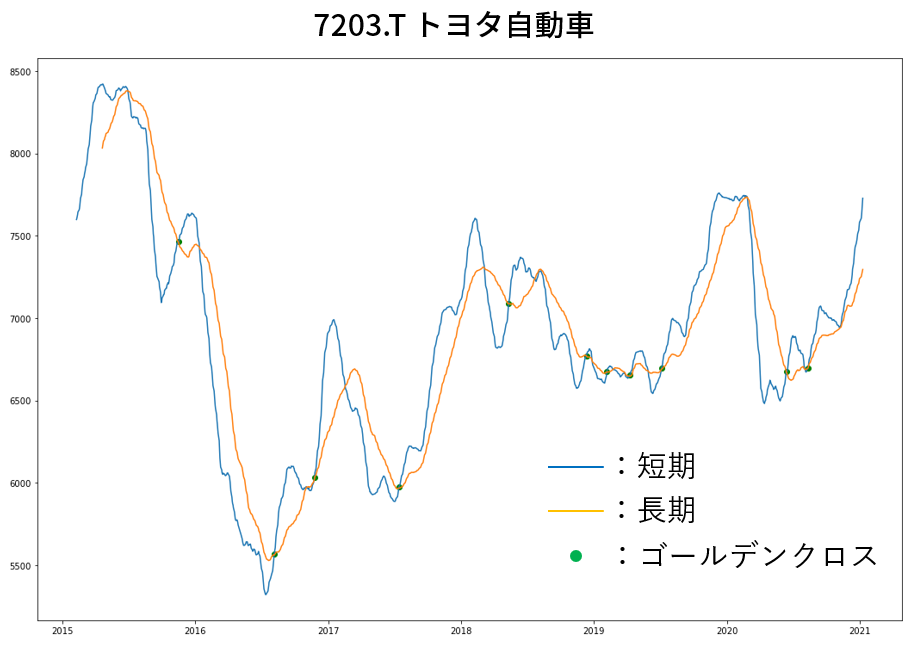
例としてトヨタ自動車の場合を記載します。
緑の丸がゴールデンクロスのタイミングを示します。
ゴールデンクロス:短期の移動平均が長期の移動平均を下から上に突き抜ける現象
⇒ 青線が黄線を下から上に突破
▼短期:25日移動平均, 長期:75日移動平均の場合
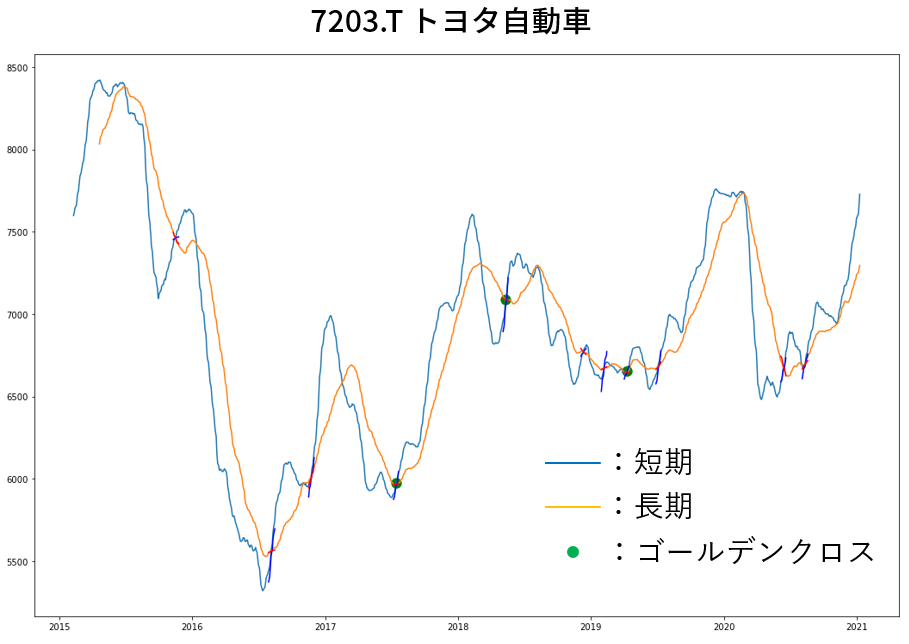
次は信頼度を検証するために条件をつけてゴールデンクロスを取捨選択します。
下図は角度:45度以上のゴールデンクロスのみにしたものです。
▼交差の条件からゴールデンクロスを選択(角度:45度以上の場合)
最後に選択されたタイミングから〇日後上昇しているか確認します。
以上の方法でTOPIX500銘柄を対象に5年分のデータを検証しました。
※検証のPythonプログラムは記事の最後に記載
検証結果
ここでは結果の一部を記載します。
その他の結果は記事の最後にまとめて記載します。
使用するデータは前述の通りTOPIX500銘柄の5年間です。
【移動平均の期間】
- 短期:5日,長期:25日
- 短期:25日,長期:75日
【株価の上昇を確認する日】
- 1日後
- 3日後
- 5日後
- 10日後
【条件】
- なし
- 方向:短期線が上向き,長期線も上向き
- 角度:45度以上
早速ですが結果を表にまとめました。
<結果>
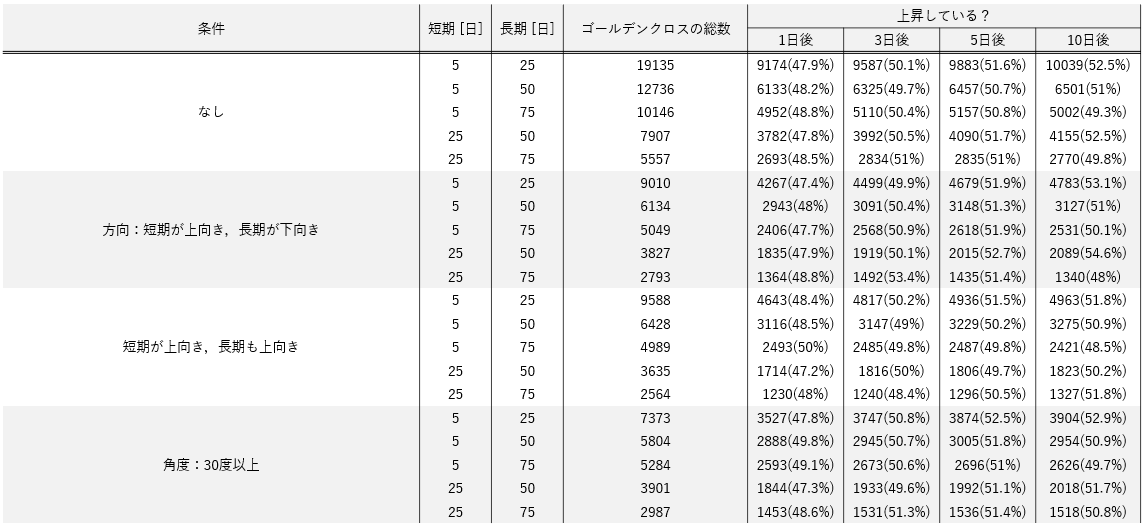
▼短期:5日,長期:25日の結果
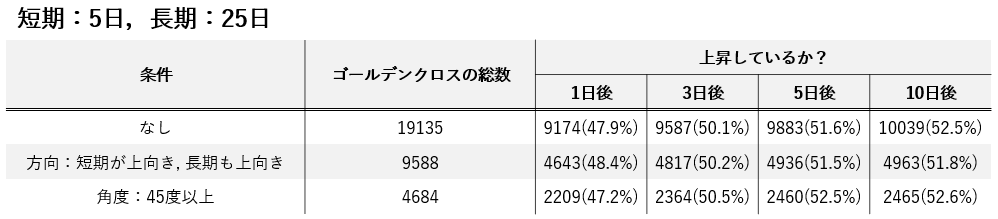
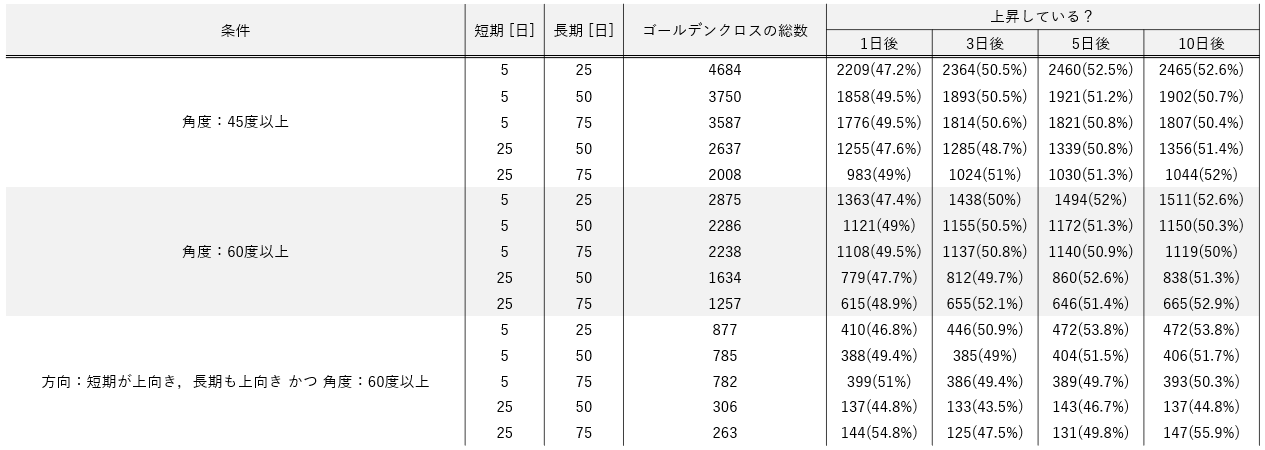
▼短期:25日,長期:75日の結果

表の通り、いずれの場合も**〇日後に上昇している確率は約50%**という結果が得られました。
条件がある/なしに関わらず約50%です。
ゴールデンクロスも信頼度も全く意味がないことが分かります。
記事の最後に記載していますが、短期,長期の期間/信頼度の条件を変更しても同様の結果となります。
ゴールデンクロスの意味とは?...
まとめ
買いサインとして最も有名なゴールデンクロスについて検証したところ、ゴールデンクロスも信頼度も全く意味がないことが分かりました。移動平均は一定期間の価格の平均値を線で結んだもののため、移動平均線の動きは価格の動きよりも遅延します。そのためゴールデンクロスでは買うタイミングとしては遅すぎると考えられます。
また、ゴールデンクロス前にその株式を所有する賢い投資家は「ゴールデンクロスが出たから買いサインだ」と考える一般の投資家が多いことを知っています。そのため、賢い投資家は「ゴールデンクロスは売りサインだ」と真逆に考え、仕込んでおいた株を売るわけです。
その養分にならないように、ゴールデンクロス単体だけでは買いタイミングを判断しないことをお勧めします。
次は
単純な移動平均のゴールデンクロスでは買いタイミングとして遅すぎるということが明らかになりました。
そこで遅延が少ない指数移動平均を使用するMACDならばどうなるのかを検証してみたいと思います。
MACDについても検証しました
【5年分データ分析】MACDの買いサインから上がる確率を検証しました
結果の一覧
検証条件と結果の一覧
【検証期間】
2015年1月1日~2020年1月8日の約5年間
【対象銘柄】
TOPIX500銘柄
【移動平均の期間】
- 短期:5日,長期:25日
- 短期:5日,長期:50日
- 短期:5日,長期:75日
- 短期:25日,長期:50日
- 短期:25日,長期:75日
【株価の上昇を確認する日】
- 1日後
- 3日後
- 5日後
- 10日後
【条件】
- なし
- 方向:短期線が上向き,長期線が下向き
- 方向:短期線が上向き,長期線も上向き
- 角度:30度以上
- 角度:45度以上
- 角度:60度以上
- 方向:短期線が上向き,長期線も上向き かつ 角度:60度以上
検証プログラム
# 株価分析用に自作した関数をまとめたもの
from trade_module import trade_module as tm
import pandas as pd
import numpy as np
# 銘柄コードの読み込み
stock = tm.get_topix500()
## resultデータフレーム作成
day = [1,3,5,10] # 〇日後に上昇しているかの〇を設定
col=["g_p_count"] # ゴールデンクロスの総数
period = [[5,25],[5,50],[5,75],[25,50],[25,75]] # 移動平均の期間
for d in day:
col.append("roc_d"+str(d)+"_plus")
result = pd.DataFrame(data=0,index=range(len(period)),columns=col)
for p in range(len(period)):
for code in stock.code:
print(code)
# 用意した株価データの読み込み
data = pd.read_csv("./data/"+code+".csv",index_col=0, parse_dates=True)
# 単純移動平均を計算
tm.add_sma_tmp(data, period=(period[p][0],50,period[p][1]))
data["g_point"] = False
# ゴールデンクロスのタイミングを取得
for i in range(len(data.index)-1):
if(data.sma_s[i]<data.sma_l[i] and data.sma_s[i+1]>data.sma_l[i+1]):
data["g_point"].iat[i+1] = True
# ゴールデンクロス時の傾き/角度を算出
data["sma_s_line"] = np.nan
data["sma_l_line"] = np.nan
data["sma_s_slop"] = np.nan
data["sma_l_slop"] = np.nan
data["sma_deg"] = np.nan
for g in data.index[data.g_point]:
# 2点間の直線を算出
a1 = data.sma_s[g] - data.sma_s[len(data.Close[:g])-1-1]
b1 = data.sma_s[g] - a1*len(data.Close[:g])
data["sma_s_slop"].at[g]=a1
a2 = data.sma_l[g] - data.sma_l[len(data.Close[:g])-1-1]
b2 = data.sma_l[g] - a2*len(data.Close[:g])
data["sma_l_slop"].at[g]=a2
data["sma_deg"].at[g] = np.rad2deg(np.arctan(abs((a1-a2)/(1+a1*a2))))
# plot用に直線データ追加
for i in range(11):
x = len(data.Close[:g])-1+i-5
if(x<=len(data.Close)-1):
data["sma_s_line"].iat[x]= a1*x+b1
data["sma_l_line"].iat[x]= a2*x+b2
# 除くゴールデンクロスを選択
for g in data.index[data.g_point]:
# 角度の条件設定
if(data["sma_deg"].at[g] < 60):
data["g_point"].at[g] = False
# 向き(傾き)の条件設定
if(not(data["sma_s_slop"].at[g]>0 and data["sma_l_slop"].at[g]>0)):
data["g_point"].at[g] = False
# 〇日後に上昇しているか確認
for g in data.index[data.g_point]:
for d in day:
if(len(data.Close[:g])+d<=len(data.Close)):
data.at[g,"roc_d"+str(d)] = (data.Close[len(data.Close[:g])+d-1]-data.Close[g])/data.Close[g]*100
else:
data.at[g,"roc_d"+str(d)] = (data.Close[-1]-data.Close[g])/data.Close[g]*100
if(data.at[g,"roc_d"+str(d)]>0):
data.at[g,"roc_d"+str(d)+"_point"] = 1
else:
data.at[g,"roc_d"+str(d)+"_point"] = 0
# 上昇していたらカウンタを加算
data.dropna(inplace=True)
if(len(data.index[data.g_point])>0):
result["g_p_count"].iat[p] += len(data.index)
for d in day:
result["roc_d"+str(d)+"_plus"].iat[p]+=sum(data["roc_d"+str(d)+"_point"])
print(result)