日経平均株価の30%は5銘柄で決まることを投資先選びに生かせるか？

＜あらすじ＞
日経平均株価の値動きは225銘柄すべての値動きが均等に影響しているわけではない。
2020年11月30日時点で値動きの約30%を上位5銘柄が占める。
値動きに各銘柄が与える影響「寄与度」と連動する度合「相関」の関係を調査する。

仮説：寄与度が高い銘柄ほど日経平均株価の値動きに連動する
結論：寄与度1位よりも相関が高い銘柄が複数存在する

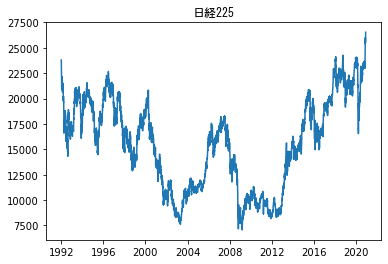
日経平均株価

日本の株式市場を代表する株価指標の1つ
世界で3番目の規模を誇る東京証券取引所、その1部に上場する企業から日本経済新聞社が選定した225銘柄の平均株価

近頃、至る所で日経平均株価の急騰が報道されています。

日経平均続伸、29年半ぶりの高値

2020年11月26日に1991年4月以来およそ29年半ぶりの高値を更新した。
新型コロナウイルスのワクチン開発の進展期待が広がるなか、各国政府や中央銀行による景気対策も続くとの見方が投資家の心理を上向かせた。
引用元：日本経済新聞

新型コロナウイルスのワクチン開発への期待や、各国の景気対策が続くとの見方が相場を支えた。
市場では「国内主要企業の業績は回復基調にあり、当面、株価は底堅い展開が続く」（大手証券）との見方も出ている。
引用元：読売新聞

実態経済との乖離

絶好調の日経平均株価とは裏腹に日本の景気が上昇していると感じる人は少ないのではないでしょうか。株価と景気にはタイムラグがあるからなのか。いや、ワクチン開発が進展したとしても、当分は流行前の景気水準には戻らない。
戻ったとしても流行前以上に景気が良くなるのか、そもそも流行前は景気が上昇していたのかもわからない。
このような状況にも関わらず、何が日経平均株価を上昇させているのか疑問に感じました。

そんな時に日経平均株価の値動きには各構成銘柄で影響力に偏りがあることを知りました。
＝ 寄与度の重み
この寄与度の重みが高い銘柄ほど日経平均株価の値動きと連動するのではないかと考えられます。
また、寄与度の重みを投資先選びに何か生かせないかというのが今回の目的です。

寄与度

まず、日経平均株価の算出方法の基本的な考え方は
$$日経平均株価の基本＝\frac{構成銘柄の株価合計}{銘柄数:225}$$
であり、名前の通り株価の平均値です。
実際には、株価の変動を調整して正しく株価を表すために
・「除数の修正」
・「みなし額面による調整」
が施されます。詳細は省略しますがこちらで解説されています。
この2つを考慮した日経平均株価の算出方法は以下の通りです。

\begin{align}
日経平均株価&=\frac{構成銘柄の採用株価合計}{除数}\\
各構成銘柄の採用株価 &= 株価\times \frac{50 [円]}{みなし額面 [円]}
\end{align}

次に寄与度とは、1つの要素の増減が全体のデータをどれだけ増減させたかを表し、日経平均株価の場合は次のようになります。
$$ある銘柄の寄与度=\frac{現在の採用株価-前日の採用株価}{除数}$$
これらからわかることは、時価総額の比重を考慮していないため株価が高い銘柄の影響を受けやすいということです。
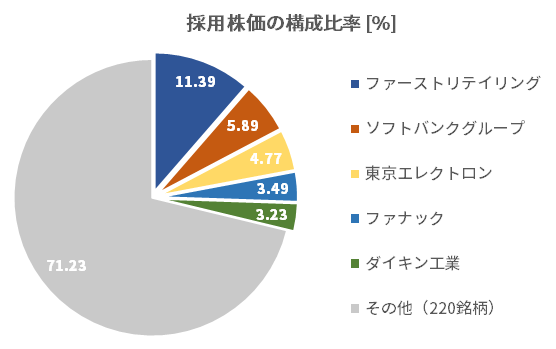
詳しく述べると、各銘柄の採用株価の構成比率がそのまま寄与度の重み（＝影響力の強さ）を表します。

下図は2020年11月30日時点の採用株価の構成比率の円グラフであり、上位5銘柄が値動きの約30%を占めていることを示します。（使用データ）

相関

日経平均株価と各銘柄の値動きが連動する度合として相関係数を使用します。
相関係数の詳しい説明はこちらで紹介されていますので、計算プログラムのみ記載します。
内容は全体の期間と計算に使用する幅（日数）を設定し、その日数ごとに計算した相関の平均を求めます。
【例】
・全体の期間　　　　　　　：100日
・計算に使用する幅（日数）：10日
1~10日,2~11日,3~12日,...,91~100日の計91通り相関を計算後、その平均値を求める

※ Pythonに慣れていないため拙いですがご容赦ください。
また、株価データの取得プログラムについては以前書いたこちらをご参照ください。

cal_correlation.py

import pandas as pd
import numpy as np

# 正規化
def normalized(data):
    n_data = data
    start = data.iloc[0,0]
    n_data.iloc[:,0] = data.iloc[:,0]/start
    start = data.iloc[0,1]
    n_data.iloc[:,1] = data.iloc[:,1]/start
    return n_data

# 相関計算
def cal_correlation(data1, data2, width):
    cor = []
    for i in range(len(data1)-width+1):
        x = np.array(data1[i:i+width])
        y = np.array(data2[i:i+width])
        cor.append(np.corrcoef(x,y)[0,1])
    return cor

## パラメータ
code = 4151             # 計算する銘柄のコード
start_date = "2019"     # 相関計算し始める日付
width = 10              # 相関計算の幅

# 用意した終値の読み込み    
read_data = pd.read_csv("nikkei225_all_closes.csv",index_col=0, parse_dates=True)
data = read_data[start_date:]
# 用意したコードと銘柄名の読み込み  
stocks_name = pd.read_csv("nikkei225_all_code.csv", header=None, names=("code","name"), index_col=0, engine="python")

# 計算する銘柄の選択, 欠損値の削除, 正規化
target = data[["^N225",str(code)+".T"]]
target = target.dropna(how="any")   
target = normalized(target) 

# 相関計算
cor = cal_correlation(target.iloc[:,0], target.iloc[:,1], width)

寄与度と相関の関係

例として
・全体の期間　　　　　　　：3ヵ月
・計算に使用する幅（日数）：10日
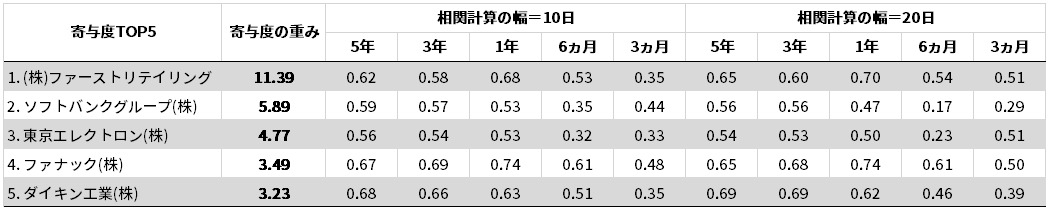
での全225銘柄の寄与度の重みと相関の関係を示します。（※ 別の設定での結果は記事の最後に記載）

▼上位5銘柄をピックアップ

▼全225銘柄の寄与度の重みと相関の関係（横軸：構成比率, 縦軸：相関の平均）

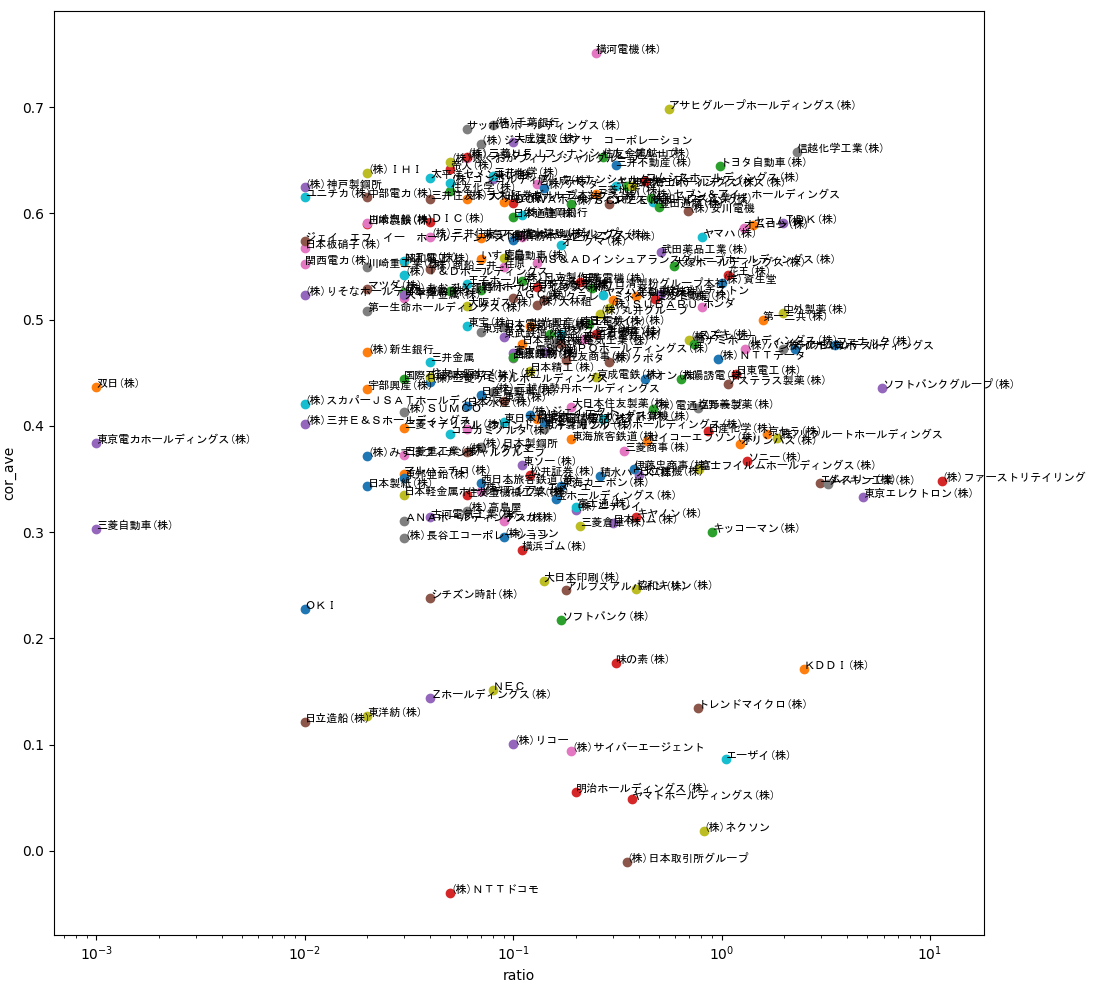
考察

採用株価の構成比率である「寄与度の重み」と連動する度合「相関」の関係を調べることで、寄与度が高い銘柄ほど日経平均株価の値動きに連動するという仮説は間違っていたことがわかりました。また、採用株価の構成比率は上位5銘柄が約30%を占めているにもかかわらず、相関の上位5銘柄は構成比率が1%にも満たない銘柄で埋められました。
「寄与度の重み」と「相関」を結び付けて投資先選びに生かすのは厳しそうですね...
ただし、
・日経平均株価の値動きには各構成銘柄で影響力に偏りがある
・その上位5銘柄よりも相関が高い銘柄が複数存在する
という事実を確認できたので良しとします。

以上の結果から「寄与度の重み」と「相関」を個別の指標として、投資先選びや値動きの予測に生かせないか考えてみました。

「寄与度の重み」
・寄与度の重みが高い銘柄が急騰/急落したときに日経平均先物や日経平均が連動指標のETFを取引
・短期的にはファーストリテイリングの急騰/急落が日経平均株価の値動きに特に寄与する
・寄与度の重みが高い銘柄の決算発表などイベント時には日経平均株価に関する取引のリスクが増加

「相関」
・日経平均先物の値動きから相関が上位の銘柄の値動きを予測
・長期的に相関が高い銘柄（豊田通商, 日本ガイシ）が日経平均株価と逆の動きをしたときに日経平均先物や日経平均が連動指標のETFを取引
※相関関係と因果関係が別物のであることには注意 （解説）

次は

値動きに各銘柄が与える影響「寄与度」と連動する度合「相関」の関係を調査したところ、その2つを結び付けて投資先選びに生かすことは困難でした。しかし、個別の指標としてはまだまだ活用の余地があるのではないかと考えています。
この記事では完全に自分の疑問に対する調査でしたが、引き続き投資先選びの指標を見つけるべく検証していきたいと思います。

今後の予定
・「S&P500が暴落したときに上昇する銘柄/インデックス/金融商品の調査」
・「日経平均株価と各銘柄のチャートを数日ずらした状態で相関を求め値動きを予想」

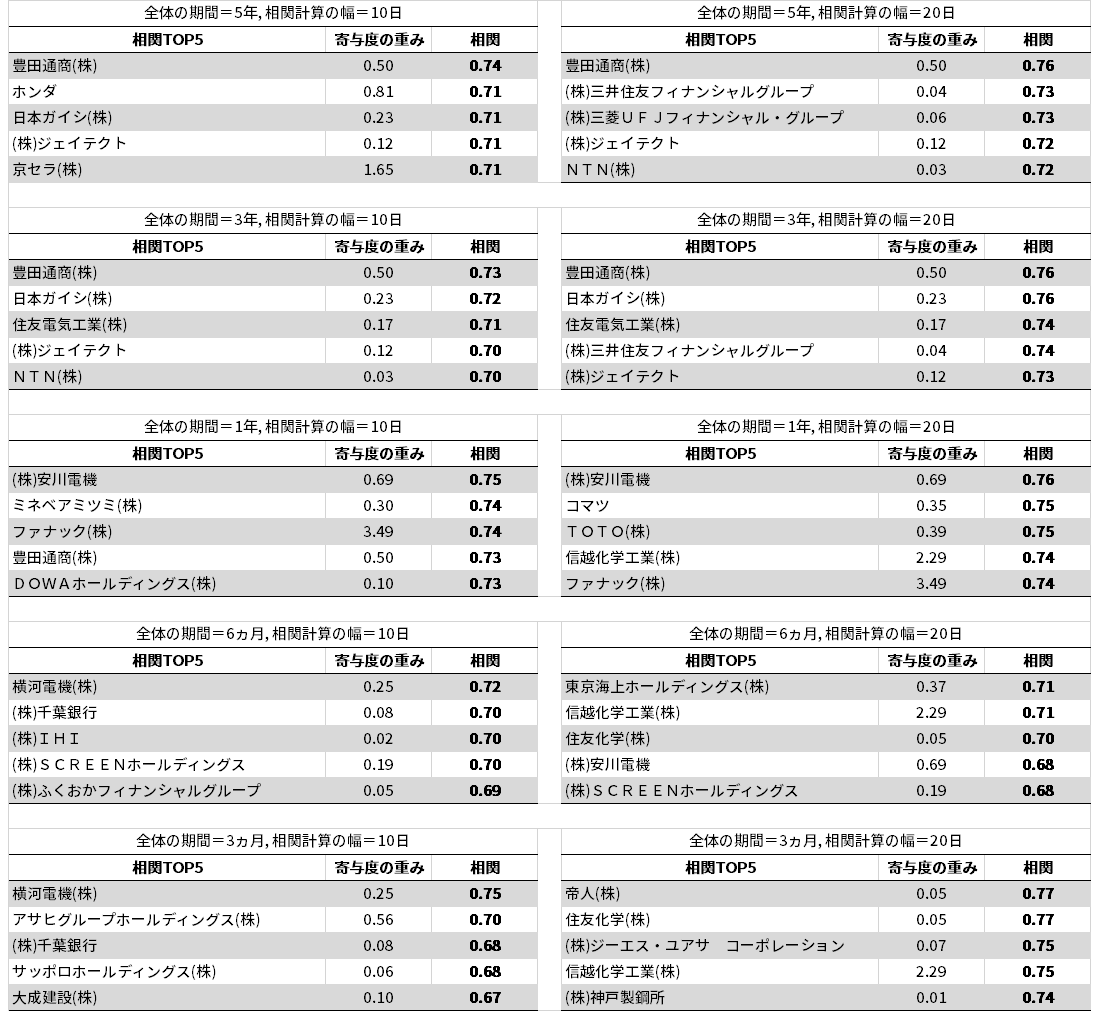
結果の一覧

相関計算の設定を変化させた場合のTop5の結果一覧を示します。
＜パラメータ＞
・全体の期間　　　　　　　：5年,3年,1年,6ヵ月,3ヵ月
・計算に使用する幅（日数）：10日, 20日

▼寄与度TOP5銘柄の結果一覧

▼相関TOP5銘柄の結果一覧