はじめに
すべての資産を株式に投資してしまうと，経済が悪化した際に，資産が大きく激減するリスクがあります．逆に，すべての資産を預金しているだけでは資産を増やしていけません（大手銀行の預金金利は0.001%程度）．
一般に債券などの他の金融商品を利用し，リスクを分散させます．株式の価値が下がったとしても，他の商品に投資していれば，資産が激減するリスクを防ぐことができます．
分散投資をする際に金融商品を以下の3つに分けて考えます．それぞれの金融商品は値動きが異なる傾向にあるものです．
・株，社債，不動産：経済が上がっていくと上がる
・国債（米国，欧州など）：安全投資（経済が悪化しているとき持った方が良い）
・コモディティ（金，銀，プラチナ，ビットコイン）：物価が上昇するとそれにともなって値上がり（インフレに強い）
今回は上記から各1つずつ株，米国債，金へ投資したとき，
・どんな比率で投資すればリスクを最小化できるか
・3銘柄への投資によって効率のより良い投資が実現できるか
について検証しました．
以前，分散投資でリスク回避の仕方【2銘柄編】で，株式と金（ゴールド）の2銘柄へ投資した場合の記事についても書いたので，興味ある方はそちらもご覧ください．
検証内容
ある5つの期間（詳細は以下に記載）で1日ごとに株式：S&P500，金（ゴールド）：SPDRゴールド・シェア（ETF），債券：iシェアーズ・コア 米国債7-10年（ETF）の時系列データを取得します．
取得したデータから，日々の収益率(%)を計算し，その日々の収益率から平均値（＝期待収益率）と分散（＝リスク）を計算します．今回の記事では収益率を年率換算せず，1日で得られる収益率で分析しています．
その平均値や分散を基にして，株式，金（ゴールド），債券に$x$，$y$，$z$の比率で投資したときの資産（ポートフォリオ）の期待収益率とリスクを計算します．$x+y+z=1$となるよう選ぶとします．
そこから，どの資産構成（ポートフォリオ）であればリスクが抑えられるか，効率よく投資がおこなえるかを検証していきます．
検証期間
・1年間：2019年12月01日から2020年11月30日まで（コロナウイルス感染拡大を含む1年間）
・1年間：2019年01月01日から2019年12月31日まで（コロナウイルス感染拡大前の1年間）
・3年間：2017年12月1日から2020年11月30日まで
・8か月：2020年4月1日から2020年11月30日まで
・4か月：2020年8月1日から2020年11月30日まで
検証結果
以下は検証結果です．計算方法，分析方法は記事の最後に紹介しています．
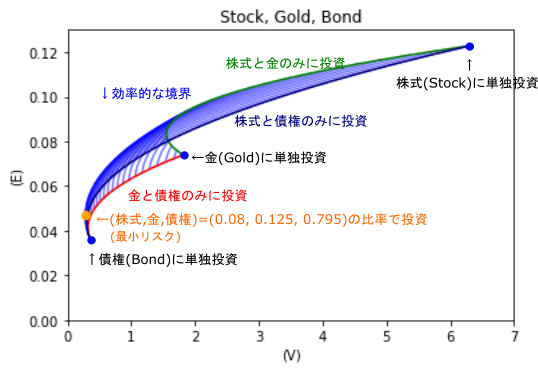
3銘柄へ投資した際の各ポートフォリオの期待収益率とリスクの関係を示しています（縦軸：期待収益率$E$，横軸：分散$V$）．
- 検証期間：1年間（2019年12月1日から2020年11月30日まで）
＜グラフの見方＞
・緑色の線：株式と金（ゴールド）のみに投資したときのポートフォリオ（$x+y=1$かつ$z=0$）
・赤色の線：金（ゴールド）と債券のみに投資したときのポートフォリオ（$y+z=1$かつ$x=0$）
・紺色の線：株式と債券のみに投資したときのポートフォリオ（$x+z=1$かつ$y=0$）
・青色の斜線部：$x$，$y$，$z$を任意に選ぶとき，ポートフォリオが実現可能な収益率とリスクの関係
・青色の点：株式，金（ゴールド），債券へいずれかに単独投資するポートフォリオ（$(x,y,z)=(1,0,0)$/$(0,1,0)$/$(0,0,1)$）
・オレンジ色の点：リスクを最小化するようなポートフォリオ
＜考察＞
3銘柄への投資によって，リスクをより小さくできるポートフォリオを構築することができます．それはオレンジ点で示されたポートフォリオです（$(株式，金，債券)=(0.08,0.125,0.795)$）．このときポートフォリオの期待収益率は0.279，分散は0.047です．2銘柄のみへの投資では実現できないリスク（分散）の小ささとなっています．
と言うのも、3銘柄への投資によって新たに「効率的な境界」を構築することができます．それはオレンジ点から株式への単独投資を示す青点までの曲線の部分です．効率的な境界の青色の部分は，2銘柄のみへの投資では実現することができない部分です．
したがって，3銘柄に投資することで，新たに「効率的な境界」の範囲が増えたので，より自分に合ったポートフォリオを選択できるようになったといえます．
また，以上のことから，債券や金にそれぞれに単独投資したり，債券と金へ2銘柄のみに投資することは効率はあまり良くないといえます．
※ コロナウイルス拡大時期を含む期間なので，他の期間と比べて，収益率の分散$V$がとても高くなっています．
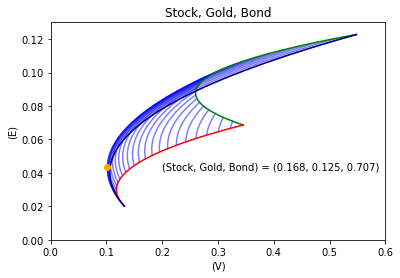
以下は上の期間と別の期間での検証結果です．
コロナウイルス感染拡大前の1年間や3年間（2017年12月1日から2020年11月30日まで）も上の結果と同様のことが言えます．
-
検証期間：1年間，コロナウイルス感染拡大前の1年間（2019年1月1日から2019年12月31日まで）
-
検証期間：3年間（2017年12月1日から2020年11月30日まで）
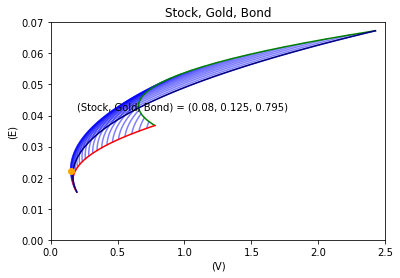
以下は直近8か月間，4か月間で検証した結果です．
これらの結果は上記の結果とは異なり，債券と株式の2銘柄へ投資すべきということを示しています．それは効率的な境界は青色の線ではなく，債券と株式のみのポートフォリオを意味する紺色となっているためです．この8か月間，4か月間では金は大幅に下落している時期なので，金に投資すべきでないということは理解できます．
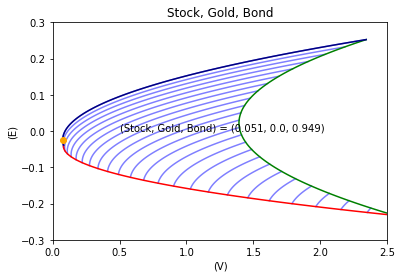
検証期間：8か月間（2020年4月1日から2020年11月30日まで）
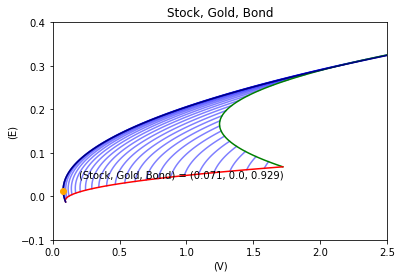
検証期間：4か月間（2020年8月1日から2020年11月30日まで）
計算方法
期待収益率とリスク（分散）の計算方法
ここでは，3銘柄へ投資したときの期待収益率とリスクの計算方法について示します．
※ 詳細な解説は数理ファイナンス (放送大学教材 7051)で記述されています．以下では詳しい説明は省略し要点のみを記述していきます．
3つの証券を$i=1, 2, 3$と番号付けします．各銘柄の収益率を$r_t^{(i)}(i=1,2,3)$とします．またそれらの証券への投資比率を$x_1, x_2, x_3$とします（$x_1+x_2+x_3=1$）．
したがって，投資比率$(x_1,x_2,x_3)$をもつポートフォリオ$P(x_1,x_2,x_3)$の収益率は，$x_1 r_t^{(1)}+ x_2 r_t^{(2)}+x_3 r_t^{(3)}$となります．
このとき，ある期間$T (t=1,...,T)$において，ポートフォリオ$P(x_1,x_2,x_3)$の収益率の平均値（＝期待収益率）は，
E(x_1,x_2,x_3) = x_1 \mu_1+ x_2 \mu_2+x_3 \mu_3
と計算できます．
ただし，$\mu_i$は証券$i$の収益率の期待値（平均値）は，$\mu_i = \frac{1}{T}(r_1^{(i)}+r_2^{(i)}+\cdots+r_T^{(i)})$とします．
次に，ポートフォリオ$P(x_1,x_2,x_3)$の分散値$V(x_1,x_2,x_3)$は，
V(x_1,x_2,x_3)=\sigma_{11} x_1^2 +\sigma_{22} x_2^2+\sigma_{33} x_3^2+2\sigma_{12} x_1 x_2+2\sigma_{23} x_2 x_3+2\sigma_{31} x_3 x_1
$\sigma_ii$は証券$i$の収益率の分散値，$\sigma_ij$は証券$i$と$j$の収益率の共分散とします．
サンプルプログラム（Python）
時系列データを収集する
以下のプログラムを実行すると，S&P500，SPDRゴールド･シェア（ETF），iシェアーズ・コア 米国債7-10年（ETF）の1年分のデータが得られます．
データはcsvファイル（data_StockPrice.csv）に保存されます．
データの取得には，Pythonのpandas_datareaderライブラリを使います．以下のプログラムではYahoo! Financeから，株価データを取得しています．
import pandas as pd
from pandas_datareader import data as wb
# SPDRゴールド･シェアとS&P500の名前リスト
tickers = ['1326.T' ,'^GSPC', '1482.T']
sec_data = pd.DataFrame()
# 2019-12-1から2020-11-30までの時系列データ（終値）をYahoo! Financeからダウンロード
for t in tickers:
sec_data[t] = wb.DataReader(t, data_source='yahoo', start='2019-12-1', end='2020-11-30')['Adj Close']
# ダウンロードしたデータをcsvファイルに保存
sec_data.to_csv('data_StockPrice.csv')
ポートフォリオの収益率の期待値と分散を計算する
期待値と分散の計算はPandasの機能を使い計算していきます．図の作成はmatplotlibを使用します．
以下を実行すると，上記で示した図が作成されます．
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 全銘柄の株価データを読み込み
df = pd.read_csv('data_StockPrice.csv', index_col=0)
# 銘柄
brand_x1 = '^GSPC' # sp500
brand_x2 = '1326.T' # SPDRゴールド･シェア
brand_x3 = '1482.T' # iシェアーズ・コア 米国債7-10年
# 収益率の計算
df_returns = (df-df.shift(1))/df.shift(1)*100
# 収益率の分散，平均の計算
ave = df_returns.mean()
var = df_returns.var()
# 期待収益率，分散
print('Average:'); print(ave); print()
print('Variance:'); print(var); print()
print('Covariance(Stock, Gold):', round(df_returns.cov().loc[brand_x1, brand_x2],3))
print('Covariance(Gold, Bond) :', round(df_returns.cov().loc[brand_x2, brand_x3],3))
print('Covariance(Bond, Stock):', round(df_returns.cov().loc[brand_x3, brand_x1],3))
print()
# Stock, Gold, Bond = x1, x2, 1-x1-x2 の比率で投資
E_portfolio = lambda x1, x2: x1*ave[brand_x1] + x2*ave[brand_x2] + (1-x1-x2)*ave[brand_x3]
V_portfolio = lambda x1, x2: var[brand_x1]*x1**2 + var[brand_x2]*x2**2 + var[brand_x3]*(1-x1-x2)**2\
+ 2*df_returns.cov().loc[brand_x1, brand_x2]*x1*x2\
+ 2*df_returns.cov().loc[brand_x2, brand_x3]*x2*(1-x1-x2)\
+ 2*df_returns.cov().loc[brand_x3, brand_x1]*(1-x1-x2)*x1
E_portfolio_list=[]; V_portfolio_list=[]
V_min_V = 10000
# データを生成
for x2 in np.linspace(0, 1, 25):
tmp_e_list = [E_portfolio(x1, x2) for x1 in np.linspace(0, 1-x2, 100)]
tmp_v_list = [V_portfolio(x1, x2) for x1 in np.linspace(0, 1-x2, 100)]
E_portfolio_list.append(tmp_e_list)
V_portfolio_list.append(tmp_v_list)
if V_min_V > min(tmp_v_list):
V_min_V = min(tmp_v_list)
E_min_V = tmp_e_list[tmp_v_list.index(V_min_V)]
x1_min_V = np.linspace(0, 1-x2, 100)[tmp_v_list.index(V_min_V)]
x2_min_V = x2
print(f'(min E,min V)=({round(V_min_V,3)},{round(E_min_V,3)}), (x1,x2,x3)=({round(x1_min_V, 3)},{round(x2_min_V, 3)},{round(1-x1_min_V-x2_min_V, 3)})')
# グラフ描画
for v, e in zip(V_portfolio_list, E_portfolio_list):
plt.plot(v, e, c='b', alpha=0.5)
# 債券に投資しない場合のグラフ
plt.plot([x**2*var[brand_x2]+2*x*(1-x)*df_returns.cov().loc[brand_x2, brand_x1]+(1-x)**2*var[brand_x1] for x in np.linspace(0, 1, 100)],
[x*ave[brand_x2]+(1-x)*ave[brand_x1] for x in np.linspace(0, 1, 100)], c='green')
# 株式に投資しない場合のグラフ
plt.plot([x**2*var[brand_x2]+2*x*(1-x)*df_returns.cov().loc[brand_x2, brand_x3]+(1-x)**2*var[brand_x3] for x in np.linspace(0, 1, 100)],
[x*ave[brand_x2]+(1-x)*ave[brand_x3] for x in np.linspace(0, 1, 100)], c='r')
# 金に投資しない場合のグラフ
plt.plot([x**2*var[brand_x1]+2*x*(1-x)*df_returns.cov().loc[brand_x1, brand_x3]+(1-x)**2*var[brand_x3] for x in np.linspace(0, 1, 100)],
[x*ave[brand_x1]+(1-x)*ave[brand_x3] for x in np.linspace(0, 1, 100)], c='navy')
# 点追加
plt.plot([V_min_V], [E_min_V], 'o', c='orange')
# タイトル設定
plt.title('Stock, Gold, Bond')
# 軸ラベル設定
plt.xlabel('(V)'); plt.ylabel('(E)')
plt.xlim(0,7); plt.ylim(0, 0.13)
plt.text(0.5, 0.045,'(Stock, Gold, Bond) = ({}, {}, {})'.format(round(x1_min_V, 3), round(x2_min_V, 3), round(1-x1_min_V-x2_min_V,3)))
※ Spyderでプログラムを実行すると，そのまま図が表示されるが，他の実行環境ではプログラムに少し記述を追加が必要とする場合がある．
出力結果
Average:
1326.T 0.073982
^GSPC 0.122770
1482.T 0.035510
dtype: float64
Variance:
1326.T 1.814575
^GSPC 6.292040
1482.T 0.367187
dtype: float64
Covariance(Stock, Gold): 0.432
Covariance(Gold, Bond) : 0.055
Covariance(Bond, Stock): -0.324
(min E,min V)=(0.279,0.047), (x1,x2,x3)=(0.08,0.125,0.795)
各銘柄の収益率の平均値と分散，共分散が出力されるようになっています．
・^GSPC：S&P500（Stock）の証券コード
・1326.T：SPDRゴールド・シェア（ETF）（Gold）の証券コード
・1482.T：債券：iシェアーズ・コア 米国債7-10年（ETF）（Bond）の証券コード